Turing: conflictos, espías y matemáticas
Turing: conflictos, espías y matemáticas
Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.
Énfasis: reconocer las aportaciones de Turing a las matemáticas.
¿Qué vamos a aprender?
En esta sesión conocerás la vida y obra de un personaje importante. Él ayudó a salvar miles de vidas con el uso de las matemáticas. Su nombre es Alan Turing.
Ten a la mano los siguientes materiales: cuaderno de apuntes, lápiz o bolígrafo, y goma.
Y, ante una duda, no olvides tomar nota en tu cuaderno y posteriormente corroborarlo con tu maestra, maestro o compañeros de clase.
Conocerás las respuestas a las siguientes preguntas. ¿Qué aportes realizó al mundo esta personalidad?, ¿Cuáles fueron sus estudios?, ¿Cuál fue su nacionalidad?, ¿Hace cuánto tiempo vivió?
¿Qué hacemos?
¿Conoces la criptografía?
Imagina que estás enviando mensajes a una persona. Ahora con el celular es mucho más fácil realizarlo, solo lo redactas, presionas enviar y listo.
Pero incluso hoy, los mensajes, antes de llegar a su destino, pasan por otros dispositivos antes de llegar a su destinatario. Pero eso significa que otras personas pueden leer los mensajes.
Si ese fuera el caso, ¿qué harías para lograr que sólo la persona a quien le escribes sea la única capaz de entenderlo?
Eso suena complicado, porque según expone, el mensaje es visible para todos.
Pero si con la persona que intercambias los mensajes creas un lenguaje secreto, podría mejorar la seguridad de la comunicación.
Precisamente ese es el principio de la encriptación.
Como se sabe, muchas personas utilizan el correo electrónico, así como los adultos emplean tarjetas de crédito o débito para comprar en comercios y por internet.

Estos dos medios electrónicos cuentan con un gran sistema de encriptación en el que la información viaja por un servidor de internet que, de manera segura, traslada el contenido al destinatario final.
Y así como funcionan los sistemas de encriptación, ¿se podría encriptar los mensajes?
A nivel de aplicación en tarjetas o cuentas de correo, se necesita cierto nivel técnico para su ejecución.
Sin embargo, una de las particularidades de las matemáticas es estar al alcance de todas las personas, y ampliar la compresión.
Revisa un ejemplo de cifrado con un algoritmo llamado “cifrado César”.
El “cifrado César” es uno de los métodos de codificación más antiguos y, en realidad, es muy simple. Consiste en desplazar el abecedario cierto número de posiciones.
La transformación se denomina ROTN, donde N es el número de posiciones que se desplaza, y ROT significa “ROTAR”.
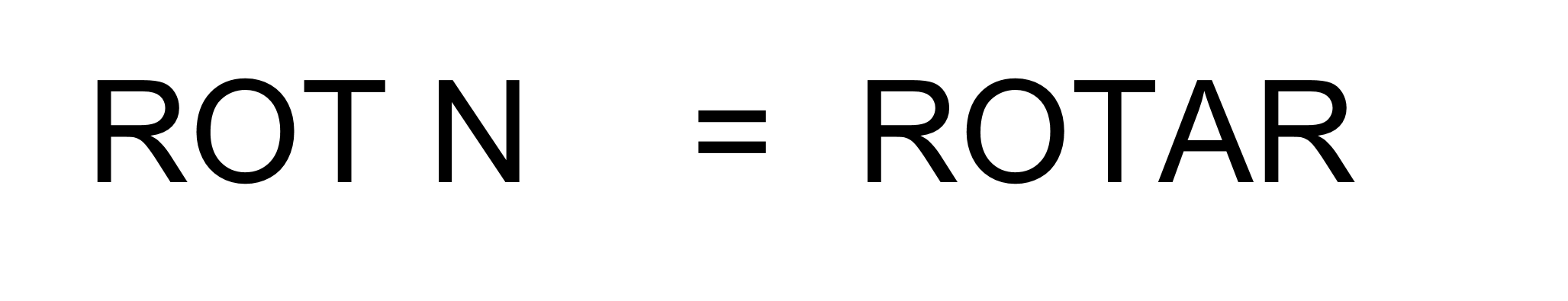
O, dicho de otro modo, las letras del abecedario se intercambian de posición.
Observa un ejemplo.
El mensaje por enviar es: “Nos vemos a las dos”.
La persona receptora del mensaje está de acuerdo en codificar el mensaje en “ROT 2”.
Y si se observa el abecedario:
Se escribe el mensaje: “Nos vemos a las dos”.
Como el código de encriptación es ROT 2, se cambia cada una de las letras del mensaje por aquella que se encuentra dos lugares después en el abecedario.
La primera letra del mensaje es “N”, y dos lugares después está la letra “O”. Entonces, en lugar de escribir “N”, escribo “O”.
La letra “O” se convierte en la letra “Q”, y la letra “S” se convierte en la letra “U”.
Con esta lógica, las siguientes letras serían:
“X”, “G”, “Ñ”, “Q” y la letra “U”.
De este modo, la letra “A” se convierte en “C”.
Y la palabra “LAS” se convierte en las letras “N”, “C” y “U.
Mientras que la palabra “DOS” se convierte en “F”, “Q” y “U”.

Realiza el siguiente ejercicio:
El mensaje cifrado es:
“ukico”, “go”, “crtgofg”, “go”, “ecuc”, “vtgu”
El mensaje se encuentra cifrado en ROT 2, es decir, cada letra del mensaje corresponde a la letra dos lugares atrás en el abecedario.
Puedes apoyarte del abecedario debajo del mensaje cifrado para resolverlo.

Ubica la letra “u” y retrocede dos espacios, es decir, a la letra “s”.
En la letra “k” se convierte en la letra “i”.
La letra “i” se convierte en la letra “g”.
La letra “c” es la tercera letra del abecedario, por lo tanto, se convierte en la letra “a”.

Y la letra “o” se convierte en la letra “n”.
La letra “g” se convierte en la letra “e” y la letra “o”, es la letra “n”.
La letra “c” es la letra “a”.
La letra “r” se convierte en la letra “p”.
La letra “t” se convierte en la letra “r”.
La letra “g”, es la letra “e”, y aquí hay dos de ellas.
La letra “o” es la “n”.
Y la letra “f” se convierte en la letra “d”.
La letra “g”, es la letra “e”.
Las letras “g” y “o”, son las letras “e” y “n”.
La letra “e” es en realidad la letra “c”; la letra “c” es la letra “a” y hay dos.
Sólo falta la letra “u”, que en realidad es la letra “s”.
Finalmente, se conocen las letras “t”, “g” y “u”, solamente faltaría la letra “v”, que se convierte en la letra “t”.
El mensaje ha sido descubierto, y dice:
“Sigan en Aprende en Casa tres”.
Este mensaje encriptado puede verse difícil a simple vista, pero no lo suficiente como para encriptar una tarjeta de crédito o un correo electrónico.
En este caso existen distintos niveles de encriptación, cada uno de mayor complejidad.
El sistema de codificación más usado en el mundo actualmente es el R S A.
Nombrado así por la primera letra de los apellidos de los matemáticos que lo inventaron: Rivest, Shamir, Adleman.

Este sistema sostiene la seguridad de los teléfonos celulares, las compras con tarjetas, entre otros casos.
Pero ¿esto tiene relación con las matemáticas?
Imagina una caja fuerte cerrada en la cual se guarda información importante; esta caja sólo se puede abrir con las llaves correctas.
El sistema cuenta con dos claves: una de ellas es la clave pública y otra es la clave privada.

La clave pública es visible para cualquier persona, mientras que la clave privada sólo es visible para el usuario.
Si la clave pública es visible para cualquier persona, ¿por qué es un sistema tan confiable a nivel mundial?
Aquí es donde las matemáticas y los números primos entran en juego.
Se sabe que los números primos son aquellos divisibles entre sí mismos y entre la unidad.
Por ejemplo, los dos números primos 13 y 17, se multiplican y el resultado es 221.
En este caso, el 221 es la clave pública de la caja fuerte; sin embargo, nadie sabe qué números primos se utilizaron para obtener dicho resultado.
En un par de horas cualquiera podría saber de qué números primos se trata, pero ¿serías capaz de encontrar los números primos que originan el número 82 919?
Cómo puedes darte cuenta, mientras más grandes sean los números primos, mayor es el producto y, por lo tanto, más complicado encontrar los números primos.
Las computadoras más modernas tardan años en encontrar los números primos más grandes.
Por ello, los matemáticos encuentran cada día números primos más y más grandes para encriptar todas las bases de datos del mundo.
Por cierto, los números primos que abren este código son mayores de 200 y menores de 300. Intenta encontrarlos.
Ahora conoce la vida del siguiente personaje.
Su nombre es Alan Mathison Turing. Nació el 23 de junio de 1912 en Londres, cerca de la estación de trenes de Paddington.
Sin embargo, a poco estuvo de residir en India, pero sus padres se decidieron por un lugar más tranquilo, una localidad en la que creció con muchas comodidades.
Como dato curioso, la casa en la que nació Turing es un hotel de 4 estrellas en la actualidad.
Su padre Julius trabajaba en la administración pública de la India, y su madre Sara Stoney provenía de una familia de ingenieros.
Esto le ayudó a tener una infancia llena de comodidades y con personas a su servicio; sus padres viajaban mucho a India y durante meses no los veía.
Desde muy pequeño le gustaba construir cosas, en una ocasión escribió una carta a sus padres con una pluma estilográfica diseñada por él y les compartió el diagrama detallado de su invento.
También hizo un prototipo poco común de la máquina de escribir y un acumulador para proporcionar energía a los faros de su bicicleta.
Siempre fue muy curioso, pero algo que alimentó aún más su curiosidad fue un libro llamado Natural wonders every child should know, que en español se traduce como Las maravillas naturales que todo niño debería conocer, de Edwin Tenney; muy popular en su época.
Fue en este libro donde, por primera vez, leyó el concepto de “máquina”. El autor del libro explicaba el cuerpo humano como una “compleja máquina que mantenía la vida”.
No fue un estudiante prodigio, siempre iba rezagado en las clases de griego, latín e inglés.
En donde sí se consideró bueno fue en las matemáticas. Ahí explotó toda su genialidad; a los 16 años ya entendía la relatividad de Einstein y se interesó por la mecánica cuántica, así que se convirtió en matemático.
Siempre recordó con cariño a su profesor Donald Eperson, a quien le gustaba mucho Alicia en el País de las Maravillas, de Lewis Carroll.
Pero no fue sino hasta la universidad, en el King´s College de Cambridge, cuando encontró su hogar intelectual.
En 1938, después de sus estudios doctorales en la Universidad de Princeton, en Estados Unidos, introdujo uno de los conceptos claves de las computadoras actuales.
Las “computadoras” en su época eran personas, empleados matemáticos, quienes realizaban los cálculos de forma repetitiva.
El diseño fue llamado “máquina de Turing”; su propósito general era distinguir de forma automatizada las funciones matemáticas que pueden ser calculadas entre las que no. Además, la máquina podía dar lectura y escribir símbolos sobre una cinta dividida en celdas, la cual representaba la memoria principal.
Y esta memoria principal es lo que se conoce como la memoria RAM de las computadoras actuales.
Esta memoria grabada funcionaba por el llamado método de dos direcciones.
Ésta se organiza desde un punto de vista «lógico», donde la posición de cada celda está identificada por un número denominado dirección de memoria.
Las órdenes ingresadas por el programador son almacenadas en la memoria de la computadora y traducidas a código máquina o binario. Esto es a una secuencia de unos y ceros, y una vez procesada, se dan los resultados.
Así, cada orden tenía asociada la posición o dirección de memoria en la que se encontraba almacenada, y la dirección de la siguiente instrucción por almacenar.
Una computadora debía cumplir con dos requisitos:
Uno, ser suficientemente rápida ejecutando cualquier programa, y dos, disponer de una cantidad de memoria satisfactoria para procesar la información.
Por ello, todas las computadoras construidas hasta el momento han intentado satisfacer estos mismos requisitos.
Se le llamó máquina universal porque la máquina podía pasar de ser una herramienta dedicada para una tarea, a ser una herramienta destinada a otra tarea distinta. Por ejemplo, de calculadora a procesador de textos, e incluso a ser un oponente en una partida de ajedrez.
Además, su “máquina universal” fue la computadora principal a bordo de las misiones del Apolo en la NASA, que permitió la llegada a la Luna el 20 de julio de 1969.
Sin embargo, se sabe que, en su época, esta máquina tuvo fines bélicos, específicamente en la Segunda Guerra Mundial.
En 1939 regresó al King´s College de Cambridge, donde lo llamaron como criptógrafo para descifrar los mensajes interceptados al ejército alemán en la instalación militar Bletchley, a 80 km al norte de Londres.
La tarea fue descifrar los códigos de la máquina alemana Enigma. Esta máquina la patentó un ingeniero alemán a finales de la Primera Guerra Mundial para encriptar mensajes, y después se vendió para encriptar transacciones comerciales. De este modo, el ejército alemán la utilizó con mejoras para la guerra y la reprodujeron.
Uno de los países más castigados por Alemania fue Polonia, pero este país capturó una máquina Enigma, y la modificaron para interceptar los mensajes encriptados.
La llamaron “Bomba”; al poco tiempo las demás máquinas Enigma fueron modificadas y por falta de recursos solicitaron a Francia e Inglaterra su apoyo para descifrar los mensajes.
Trabajó en una nueva máquina llamada “Bombe”, que pesaba casi una tonelada, con la cual reproducía el trabajo de varias Enigma. Fue así como logró descifrar todos los mensajes encriptados de los submarinos U-BOOT alemanes.
Entonces, sus aportaciones matemáticas ayudaron a dar fin a la guerra y reducir el número de víctimas.
Se sabe que, tras este acontecimiento, fue galardonado con la Orden del Imperio Británico por su contribución como criptógrafo.
Tras incorporarse a la Universidad de Manchester, encontró a su amigo Max Newman, y con el patrocinio de la Royal Society, se dedicaron a crear computadoras. Pero ahora, no para fines militares, sino para la ciencia.
Trabajó diseñando los programas de análisis numérico para resolver con la computadora problemas de cálculo, ecuaciones, matrices, entre otras cosas. Así, sus compañeros y él dieron vida a la computadora Manchester Mark I en 1948.
Por ello, la Mark I es considerada por algunos historiadores de la informática como una de las primeras computadoras modernas, y Turing es llamado “el Padre de la Computación”.
Fue la primera computadora electrónica del mundo con programas almacenados en la misma máquina.
Después lanzaron otro modelo, “Ferranti Mark I”, en 1951, una de las primeras computadoras comerciales de la historia utilizada para resolver problemas variados, tanto de índole industrial como problemas de cristalografía o de ajedrez.
Pero el auténtico reto fue una computadora capaz de hacer tareas más complejas, como traducir un texto o demostrar teoremas matemáticos.
Sin embargo, se sabe que las primeras computadoras utilizaban circuitos electrónicos para realizar operaciones tales como la multiplicación o la división.
Esa computadora sustituyó esos circuitos por programas almacenados en la máquina que realizaban esas operaciones, una idea innovadora y mucho más económica.
Por ejemplo, si se traslada esa idea a una computadora actual, se le traduce como software o aplicaciones, en el caso de los teléfonos inteligentes.
Gracias a la variedad de softwares, se pueden realizar operaciones en una hoja de cálculo, reproducir videoclips, dibujar en programas de diseño, entre otras actividades que son gracias a muchos años de avances en la tecnología y la computación.
En el trabajo de Alan Turing se observan las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.
El reto de hoy:
En tu libro de texto de Matemáticas de tercer grado se encuentran diversos problemas para ampliar tu conocimiento sobre el uso de software de una computadora.
¡Buen trabajo!
Gracias por tu esfuerzo.
