Sustracción y adición de números positivos y negativos
Aprendizaje esperado: resuelve problemas de suma y resta con números naturales, fracciones y decimales positivos y negativos.
Énfasis: dar sentido y significado a la adición y sustracción de números positivos y negativos.
¿Qué vamos a aprender?
En esta clase, retomarás algunos conocimientos sobre el tema de “sustracción y adición de números positivos y negativos”. Para lograrlo, realizarás diversas actividades con la finalidad de precisar algunas particularidades sobre este interesante tema.
En esta sesión, expondrás algunas actividades de la vida cotidiana, para ser analizadas y tomar las decisiones que convengan; o, al menos, para tener el panorama general de cada situación.
¿Qué hacemos?
Recuerda los conceptos básicos sobre el uso de números enteros, fracciones y decimales; positivos y negativos, para dar continuidad al tema.
Leonhard Paul Euler, matemático y físico, de quien se habló recientemente en Aprende en casa 3, hizo importantes descubrimientos en diversas áreas como el cálculo y la teoría de números. Gracias a Euler, se empezaron a usar de manera formal los números negativos, ya que antes eran conocidos como números deudos o absurdos; él fue el primero en usarlos. En la actualidad, se pueden ejemplificar a los números negativos como deudas de tarjeta de crédito, el dinero que se gasta o se debe, temperaturas bajo cero, profundidades debajo del nivel del mar, etcétera.
Observa cómo se utilizan los números negativos en la vida cotidiana; para ello, lee lo siguiente y exprésalo matemáticamente:
La temperatura es de 3 grados bajo cero, ¿cómo lo representarías numéricamente?
3 negativo.
Luis Mario bajó 7 kilogramos de peso; en este caso. sería 7 negativo.
Un submarino se encuentra a 450 metros de profundidad; la respuesta numérica es 450 negativo.
La temperatura superficial en Júpiter es de 150 grados bajo cero; es decir, 150 negativo.
Por último.
Un avión se encuentra a 1 200 pies de altura. La respuesta es 1 200 o 1 200 positivos, pero hay que recordar que, regularmente, al hablar de números positivos, únicamente se menciona el nombre del número y tampoco se usa el signo correspondiente.
Ahora, acomoda los números de menor a mayor valor absoluto; recuerda que estos valores se representan entre dos barras verticales. Así se tiene:
3 negativo, 7 negativo, 150 negativo, 450 negativo y 1 200.
¿Este sería el orden correcto de los números de menor a mayor?
No, porque, en los números negativos, entre mayor valor absoluto, menor valor tiene el número; es decir, los números negativos entre más retirados estén del cero son menores, entonces se tiene: -450, – 150, -7, -3 y 1200.
Ahora, para ejemplificar visualmente la aparición de los números negativos, utiliza la recta numérica. Observa:
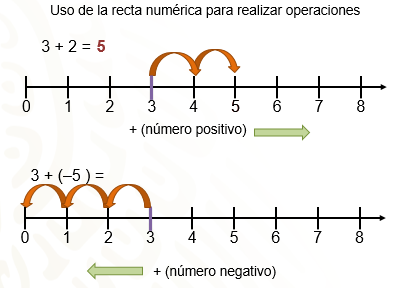
Traza una recta numérica del 0 al 8 y realiza la siguiente operación: 3 + 2 = 5.
Te sitúas en el número tres; recuerda que, para sumar un número positivo, te mueves hacia la derecha. Entonces, avanza dos unidades y llegas al cinco, que es el resultado de 3 + 2, como se observa en la recta numérica.
Ahora bien, si vas a realizar la operación de 3 + (5 negativo) observa con movimientos en la recta numérica, cuál es el resultado.
Te sitúas en el número tres, pero como en este caso se suma un número negativo, se puede considerar como un retroceso; entonces, te tienes que mover a la izquierda 5 unidades. Son 5 unidades que tienes que moverte. Efectivamente, se debe ampliar la recta numérica hacia la izquierda; es decir, hacia los números negativos.
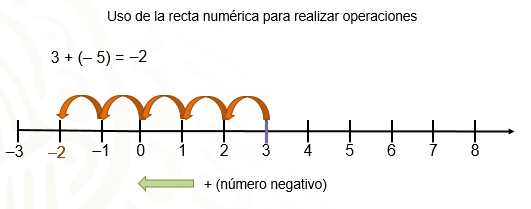
Al agregar números negativos y moverte dos unidades más a la izquierda, llegas al número 2 negativo; es decir, 3 + 5 negativo es igual a 2 negativo.
Los números negativos te ayudan a conocer lo que se debe o hace falta.
¿Cómo vas hasta aquí? ¿Ya recordaste como sumar números negativos?
Observa algunos ejemplos más.
Traza tres rectas numéricas, para representar en ellas, tres distintas operaciones:
2 + 2, 1 negativo + 3 negativo, 4 + 5 negativo.
¿Ya tienes los resultados?
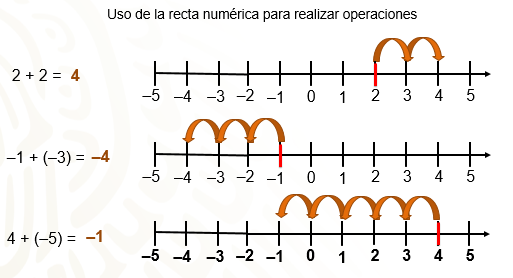
En la primera operación, te sitúas en el 2 y, como se suma un número positivo, te mueves 2 unidades a la derecha; así tienes que 2 + 2 es igual a 4.
En la segunda operación, te colocas en el 1 negativo y, como se suma un número negativo, entonces te mueves 3 unidades a la izquierda. De esta manera, 1 negativo más 3 negativo es igual a 4 negativo.
¿Podrías establecer una regla para sumar dos números positivos o dos números negativos? Toma nota, más adelante lo verificarás. Observa a la última operación. Por último, 4 + 5 negativo. Te colocas en el 4 y ¿hacia dónde tienes que moverte?
En este caso, te vuelves a mover 5 unidades a la izquierda, porque estas sumando un número negativo. Observa que el resultado de 4 + 5 negativo es igual a 1 negativo.
¿Identificaste las reglas para sumar números positivos y negativos?
La solución de las adiciones en la recta numérica te permitió justificar las reglas de la adición de números positivos y negativos.
La regla de la adición de números positivos y negativos indica que: al sumar números positivos o números negativos, se suman los valores absolutos y el resultado conserva el signo de los números en cuestión.
Al sumar un número positivo y uno negativo, se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.
Aplica lo anterior en algunas situaciones problema.
El papá de Carmen y Manuel les dice que, por cada día que realicen sus labores escolares, les dará permiso de jugar su videojuego favorito por 30 minutos; pero si no entregan sus trabajos diarios, les descontará 40 minutos de tiempo para jugar. El papá, todos los días anota el comportamiento de sus hijos y, el sábado de cada semana, realiza la cuenta para saber cuántos minutos pueden jugar la siguiente semana.
Observa cómo les fue esta semana a Manuel y a Carmen.
Manuel entregó sus trabajos escolares completos los días lunes, miércoles y viernes; mientras que el martes y jueves, no lo hizo.
Carmen realizó todas sus tareas los días martes y miércoles, pero los días lunes, jueves y viernes, no cumplió con todas las tareas.
El papá les indicó que Manuel podrá jugar por 10 minutos y Carmen debe 60 minutos.
¿Cómo es posible esto?, se preguntaron Manuel y Carmen.
¿Ya sabes cómo hizo el cálculo el papá de Carmen y Manuel?
Observa el desarrollo:
Lo que hizo, fue considerar el tiempo de las tareas cumplidas con un número positivo; es decir, 30 minutos; y las tareas incumplidas con un número negativo, 40 negativo, y sumó por separado los valores positivos y negativos de cada uno, para después sumar los resultados obtenidos.
Observa las operaciones que realizó el papá.
Empieza con el caso de Manuel: los días lunes, miércoles y viernes cumplió con todas sus tareas, esto es igual a 30 + 30 + 30 = 90 minutos; pero los días martes y jueves, no cumplió con sus tareas, entonces 40 negativo + 40 negativo = 80 minutos negativos.
Al sumar los resultados anteriores, 90 + 80 negativo, el resultado es 10, que son los 10 minutos que Manuel puede jugar.
Ahora, observa el caso de Carmen. El martes y miércoles tuvo minutos a favor, 30 + 30 = 60 minutos, pero los días lunes jueves y viernes no cumplió con sus tareas, por lo que sumó minutos en contra o negativos, 40 negativo + 40 negativo + 40 negativo = 120 negativo. Al sumar los resultados: 60 + 120 negativo = 60 negativo, que representan los 60 minutos que Carmen quedó a deber.
¿Observaste que, cuando se tienen varios números positivos y negativos en una misma operación, es más conveniente sumar los números positivos y sumar los números negativos de manera aislada y, al final, realizar la adición de los resultados?
Ahora, observa otro ejemplo de adición de números positivos y negativos.
Arturo les platicó a sus amigos que está en régimen alimenticio y haciendo ejercicio para bajar de peso, algunas semanas le va bien otras no tanto.
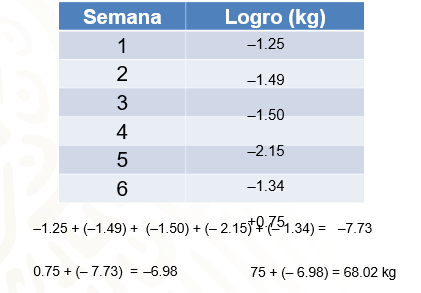
La tabla muestra sus avances semanales: la primera semana perdió 1.25 kg; en la semana 2, perdió 1.49 kg; en la 3, 1.5; para la semana 4 perdió 2.15 kg; para la 5 perdió 1.34 kg y en la semana 6 no pudo bajar, al contario, subió 0.75 kg.
¿Cuántos kg perdió?
Si antes de empezar su régimen alimenticio tenía 75 kg, ¿cuál es su masa actual?
En este caso, es más práctico sumar primero todos los números negativos: 1.25 negativo + 1.49 negativo + 1.50 negativo + 2.15 negativo + 1.34 negativo. Al realizar la adición, se obtiene 7.73 negativo.
Ahora, se suma 0.75 al resultado anterior, que son los kg que subió en la semana 6, el resultado es 6.98 negativo. Ahora, se suma a 75 kg, los kilogramos que perdió; es decir, 6.98 negativo.
75 + 6.98 negativo = 68.02, que representa la masa actual de Arturo en kilogramos.
Recuerda que, para aclarar tus dudas, puedes consultar a tu profesora o profesor a distancia; o bien, tu libro de texto.
Resuelve otra situación-problema.
Un cajero automático de un banco, inicia las operaciones del día con $100 000 en efectivo. Durante la primera hora, se realizaron varios movimientos de depósitos y retiros de dinero. Primero, fue un retiro de $5 000, luego otro retiro de $3,000, un depósito a tarjeta de crédito por $7 500, un retiro de $2 000, pago a tarjeta por $6 250, otro pago a tarjeta por $7 200 y, finalmente, un retiro por $4 000.
¿Cuánto dinero habrá en el cajero automático después de estos movimientos?
Para dar solución al problema, tienes que asignar valores negativos a los retiros, valores positivos a los pagos o depósitos y sumarlos.
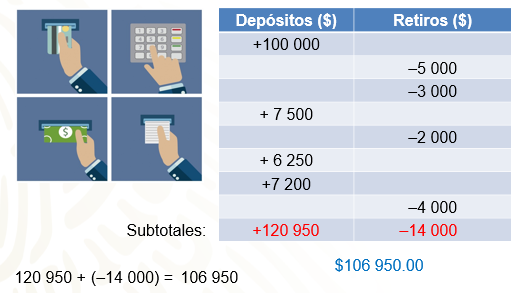
Lo más conveniente, es realizar la adición de los números positivos y de los números negativos por separado para, después, sumar los resultados.
Primero los positivos. En esta columna, se consideran los 100 000 que había originalmente en el cajero:
100 000 + 7 500 + 6 250 + 7 200 = 120 950 y también –5 000 + (–3 000) + (–2 000) + (– 4 000) = –14 000.
El resultado de 120 950 + (–14 000) = 106 950.
En el cajero automático había $106 950, transcurrida la primera hora.
Hasta ahora, has resuelto situaciones relacionadas con adiciones de números positivos y negativos, pero, ¿qué sucede con la sustracción de números positivos y negativos?
¿Cuál es el resultado de la sustracción 8 – 3?
Parece sencillo de resolver, Y, ¿cuál es el resultado de 5 negativo menos 3 negativo?
Representa las operaciones en una recta numérica.
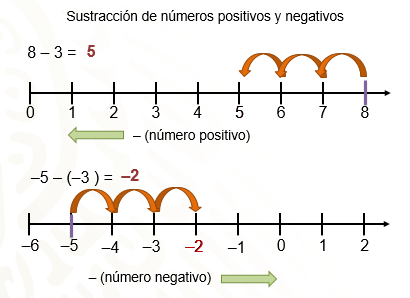
Al inicio de la sesión, viste que, para sumar un número positivo en la recta numérica, te tienes que desplazar hacia la derecha. En el caso de la sustracción, por ser la operación opuesta a la adición, te tienes que mover a la izquierda, al restar un número positivo. Por lo tanto, para la resta 8 – 3, nos ubicamos en el 8 y te desplazas 3 unidades a la izquierda llegando al 5 positivo.
En el caso de la sustracción 5 negativo menos 3 negativo, ¿hacia dónde tendrías que desplazarte? Si recuerdas, al sumar un número negativo, el desplazamiento fue a la izquierda; siguiendo la lógica anterior, entonces, para restar un número negativo, te desplazas a la derecha. Te ubicas en 5 negativo y te mueves 3 unidades a la derecha, para llegar al 2 negativo; así, 5 negativo – 3 negativo es igual a 2 negativo.
Resuelve algunos ejemplos más.
En la primera operación, 2 positivo menos 4 positivo, te sitúas en el 2 y, como se resta un número positivo, te mueves 4 unidades a la izquierda; así tienes que 2 – 4 es igual a 2 negativo.
En la segunda operación te colocas en el 1 negativo y, como se resta un número negativo, entonces te mueves 3 unidades a la derecha. De esta manera, 1 negativo menos 3 negativo es igual a 2 positivo.
Finalmente, para la sustracción, 2 menos 3 negativo, te colocas en el 2 positivo y te mueves a la derecha 3 unidades; entonces 2 menos 3 negativo es igual a 5 positivo.
Realiza la siguiente actividad para justificar el procedimiento del trabajo realizado.
Antes de continuar, recuerda que el inverso aditivo o número opuesto de un número, es aquel número que, en la recta numérica, se encuentra a la misma distancia del cero, que el primer número. Por ejemplo, 4 positivo es el opuesto o inverso aditivo de 4 negativo.
Si a un número le sumas su inverso aditivo, el resultado es cero. Observa lo anterior en la recta numérica.
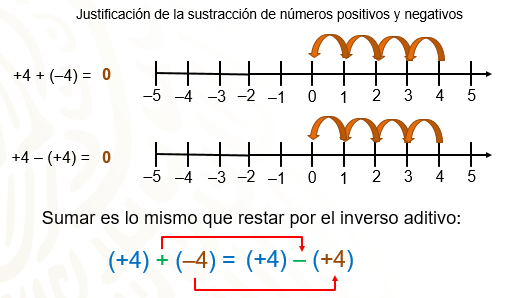
Si a 4 positivo le sumas 4 negativo, recuerda que, al sumar un número negativo en la recta, te mueves a la izquierda; entonces tienes 4 + 4 negativo es igual a cero.
Ahora, para la sustracción, 4 positivo menos 4 positivo, te ubicas en el 4 y, para restar un número positivo, también te mueves a la izquierda: 4 menos 4 = 0.
Con los ejemplos anteriores, se puede concluir que sumar un número, es lo mismo que restar a su inverso aditivo; es decir, 4 positivo más 4 negativo es igual que 4 positivo menos 4 positivo.
Con lo anterior, puedes justificar la sustracción de números positivos y negativos.
Como restar es lo mismo que sumar por inverso aditivo, la sustracción 8 positivo menos 5 negativo, puedes representarla como 8 positivo más 5 positivo, ya que 5 es el opuesto de 5 negativo; entonces, 8 – 5 negativo, es igual a 13.
Ahora, la sustracción 7 negativo menos 11 negativo, es equivalente a la adición 7 negativo más 11 positivo. Para resolver esta operación, aplicas la regla de la adición y el resultado es 3 positivo; entonces, 7 negativo menos 11 negativo es igual a 3 positivo.
Con lo visto, ya puedes justificar la regla de la sustracción que indica que: restar un número positivo o número negativo, es lo mismo que sumar su opuesto o inverso aditivo.
Para poner en práctica el trabajo sobre la adición y la sustracción de números positivos y negativos, realiza la siguiente actividad.
En un grupo de secundaria, realizaron un juego llamado “El saldo de la caja”, con las siguientes indicaciones:
Se elaboraron tarjetas con números entre –50 y +50.
Los números positivos representan dinero que se tiene o saldo a favor y los números negativos dinero que se debe o saldo en contra.
Se toman 2 tarjetas las cuales se tienen que sumar para establecer un saldo inicial.
Posteriormente, se toman una tercera tarjeta, cuyo valor se debe restar.
Observa un ejemplo para entender las reglas. Resuelve las operaciones para practicar.

Considera el siguiente ejemplo. Se sacan las tarjetas, en pesos, de 28 y 35 negativo, las cuales se tienen que sumar para conocer el saldo inicial:
28 + 35 negativo es igual a 7 negativo, lo que significa que el saldo es en contra o que se deben 7 pesos.
Ahora, observa la tercera tarjeta, es 15 positivo, que representa un gasto que se hizo y no se descontó, por ello se hace una resta, ya que representa algo que se debe.
Entonces, 7 negativo menos 15 es igual a sumar, 7 negativo más 15 negativo, que es igual a 22 negativo. Así, el saldo final es de 22 pesos negativos.

Observa otro ejemplo. Las primeras tarjetas son 12 negativo y 35; al sumarlas, el resultado es 23; es decir, el saldo inicial son 23 pesos a favor.
La tercera tarjeta es 20 negativo, que representa un gasto que no se hizo; por lo que se descuenta del saldo inicial, así que se resta.
Entonces, al resolver las operaciones, se puede ver que, en este caso, el saldo final es de 43 pesos a favor.
Con esta actividad has llegado al final de la sesión.
El reto de hoy:
En casa puedes elaborar tarjetas para realizar una actividad similar a la que acabas de resolver.
Recuerda que éste es un material de apoyo y que puedes consultar otras como tu libro de texto de Matemáticas, en donde puedes encontrar más actividades relacionadas para practicar el trabajo realizado en esta sesión. No te olvides de consultar a tu maestra o maestro a la distancia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
