¿Son parecidos o semejantes?
¿Son parecidos o semejantes?
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: resolver problemas que impliquen las propiedades de semejanza de triángulos.
¿Qué vamos a aprender?
Para las matemáticas: ¿Qué es semejanza?

Congruencia: Se le llama a la propiedad que tienen dos figuras de ser exactamente iguales y semejanza es la propiedad que tienen dos figuras de ser idénticas o proporcionales.

Observa uno de los criterios de semejanza de triángulos.
El criterio LLL especifica que:
Dos triángulos son semejantes si tienen sus lados homólogos proporcionales.
Esto es que. Si te das cuenta en la imagen.
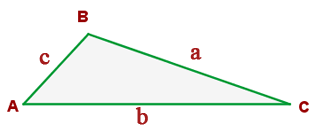
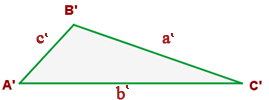
Relaciona cada lado del triángulo ABC y el triángulo A´B´C´, tal que:
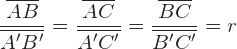
Cada una de las razones obtenidas deben ser iguales.
Entonces:
Se concluye que, si las razones entre los lados correspondientes son iguales, es porque hay una proporción igual entre sus lados y por lo tanto los triángulos son semejantes.
¿Qué hacemos?
Para fortalecer el conocimiento de este criterio, observa una demostración con un programa de geometría dinámica para que comprendas la interacción y relación directa que tienen los 2 triángulos y sus lados correspondientes.
https://www.geogebra.org/m/dW2Z7rKC
En la imagen puedes ver dos triángulos con medidas conocidas.
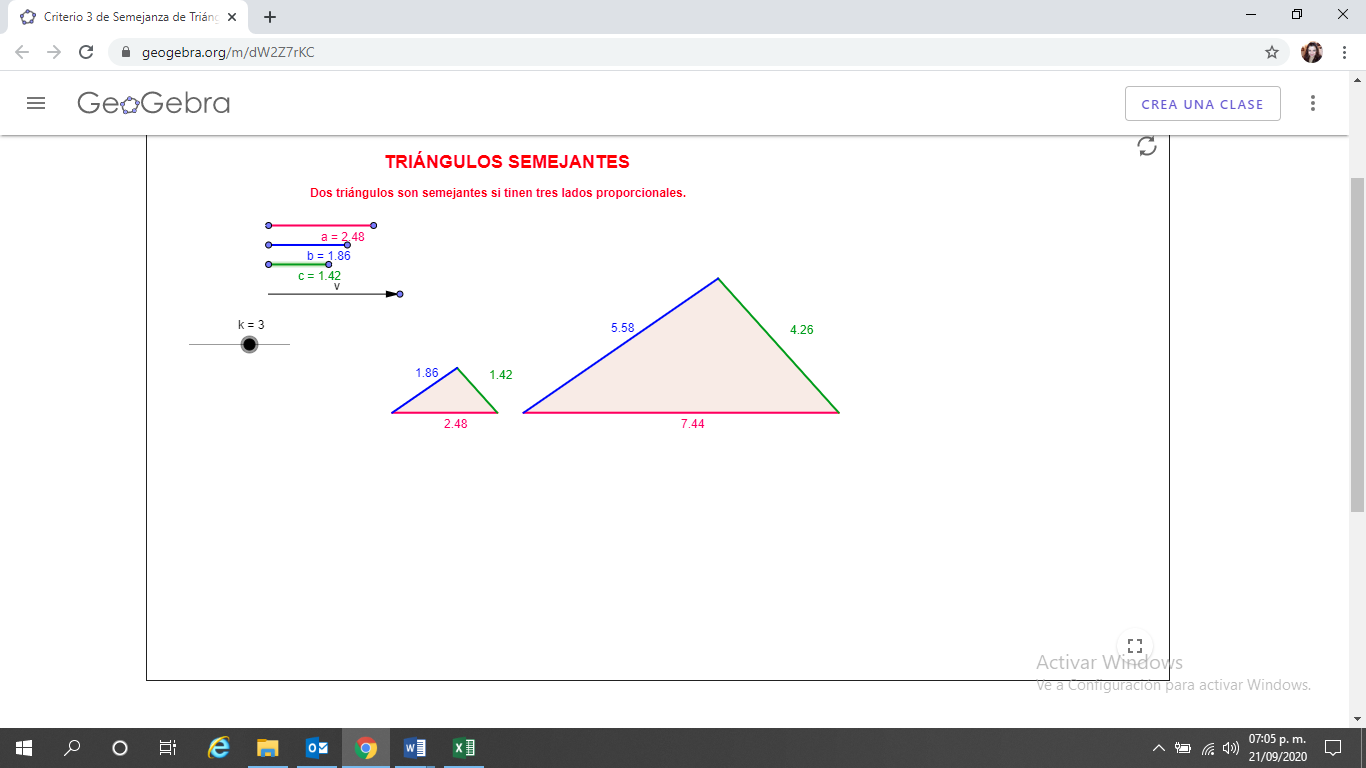
Los triángulos tienen las siguientes medidas:
La medida del lado A de color rojo del triángulo mayor es de ____ y del menor _____, la medida del lado B de color azul del triángulo mayor es de _____, y del menor es de______, y el lado C de color verde del triángulo mayor es de _______ y del menor es de _______.
La relación o razón directa entre los lados de los triángulos, así como lo observaste en el ejemplo anterior es la división de las medidas de los lados del triángulo mayor entre las medidas del triángulo menor, el valor obtenido es la proporción o razón K. En este caso, señala que la proporción que tienen es que el triángulo grande es 3 veces en tamaño que el triángulo pequeño.
Y lo puedes comprobar, ya que, por ejemplo, el lado A del triángulo pequeño tiene una medida de ______ y el mismo lado, pero del triángulo grande tiene una medida de_______, con lo que puedes comprobar dividiendo dichas cantidades, obtienes que entre los dos lados hay una proporción precisamente de 3, que es el valor de K que observas aquí.
De esta manera puedes comprobar los otros dos lados de cada triángulo y verificar que la proporción es la misma que obtienes con los lados A.
Ahora, si mueves uno de los lados del triángulo, por ejemplo, el lado A de los triángulos y observarás como al cambiar un lado de un triángulo, también cambia el mismo lado del otro, y la razón sigue siendo la misma, como sabes K no cambia. Esto mismo sucederá si cambias cualquiera de los otros lados, la razón K no cambia.
Esto demuestra la relación directa existente entre los triángulos, esta relación es de proporcionalidad y es igual a k, así se demuestra que los dos triángulos son semejantes.
Ahora si cambias la proporción K, automáticamente cambia el tamaño del triángulo grande, esto porque la relación es precisamente esa, que el triángulo grande es quien debe crecer en relación al triángulo pequeño. Y lo observas si cambias K al máximo k= 5 tienes que las medidas de los lados tienen esa proporción, de 5 veces las medidas del triángulo menor.
Y ¿Qué pasará si cambias la proporción K al mínimo hasta llegar a cero?
¿Qué pasará con el triángulo mayor?
Para terminar, mueve el triángulo grande y lo sobreponlo en el pequeño. Te das cuenta de que es como si el triángulo pequeño fuera parte del grande.
¿Cómo explicarías esto?
Anota tus respuestas en tu cuaderno y reflexiona.
¿Te diste cuenta de qué manera se comprueba la razón existente entre los lados de los 2 triángulos que se mostraron?
Te sugerimos realizar la siguiente actividad:
Necesitarás cartulina de colores, juego geométrico, marcador, lápiz y goma.
Sigue las siguientes instrucciones:
Recorta dos triángulos rectángulos con medidas, así como se muestra en la imagen.
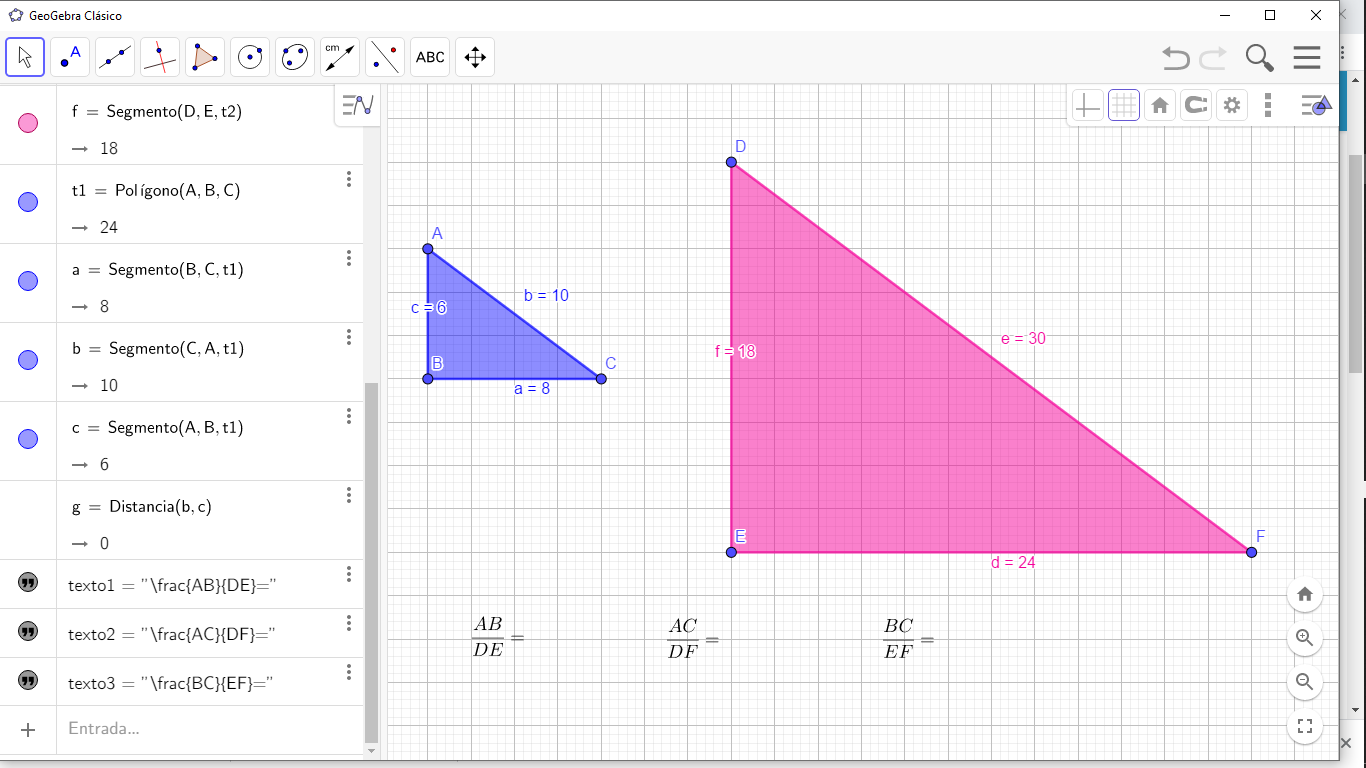
TRIANGULO 1
AB = 6 cm
AC = 10 cm
BC = 8 cm
TRIANGULO 2
DE= 18 cm
DF = 30 cm
EF = 24 CM
Te puedes apoyar de una escuadra de 60 grados como la que se muestra, ya que los triángulos deben tener la misma forma, pero no el mismo tamaño.

Ya hechos los triángulos, escribe en cada uno de ellos los datos que les corresponden: letras en los vértices y los lados y cuanto mide cada lado.
Relaciona los lados como se muestra en la imagen.
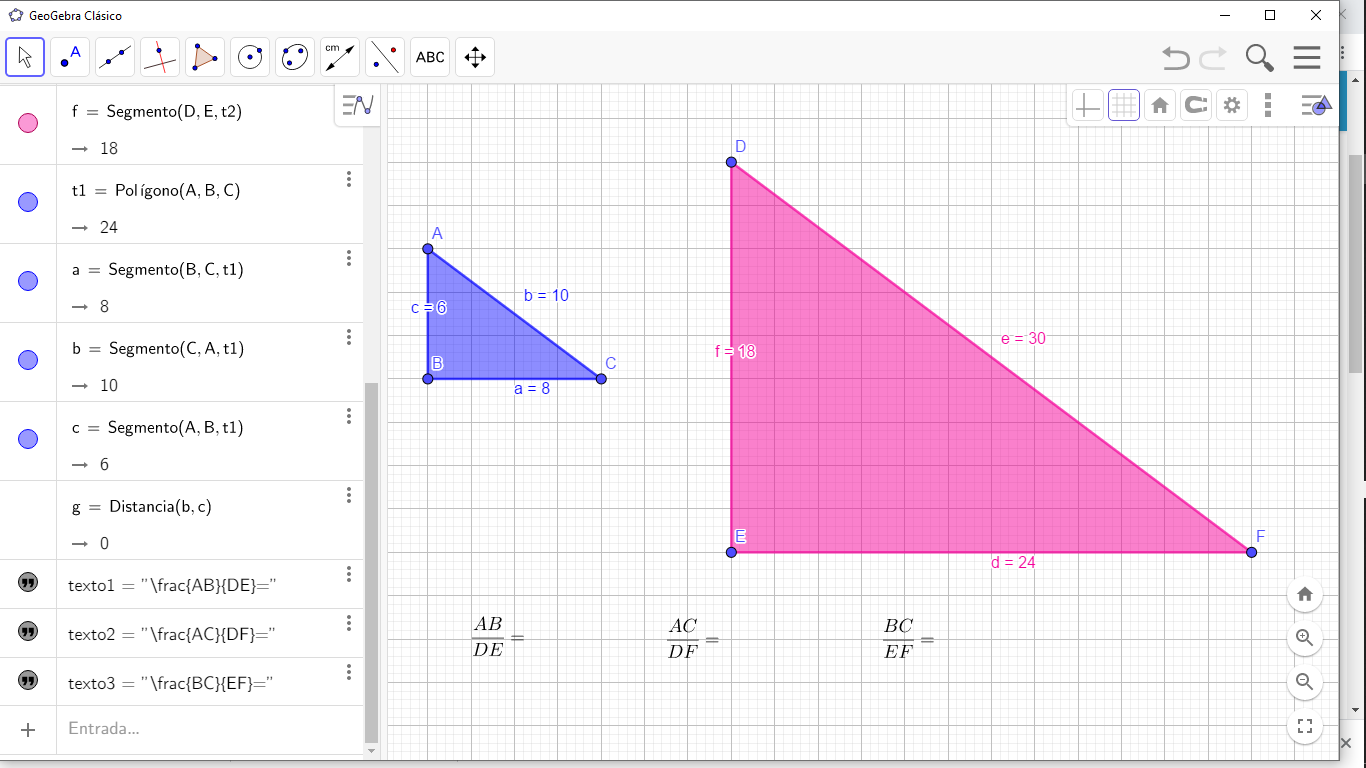
De tal manera que tengan lo siguiente:
Sustituye los valores de los lados en las proporciones y calcula las mismas.
Queda:
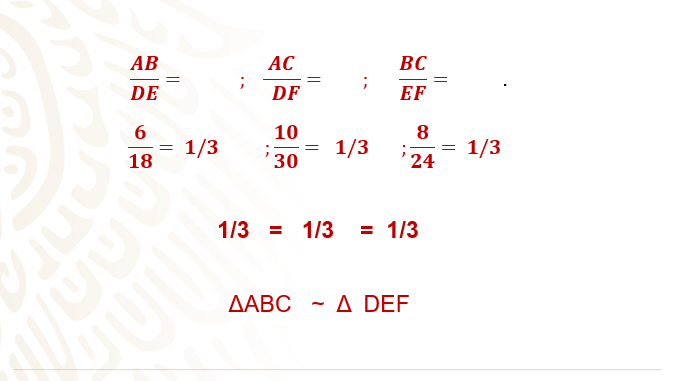
Pega tus triángulos en tu cuaderno y anota tus resultados.
Ahora la pregunta es: ¿Cómo se utiliza este criterio de semejanza en un problema real?
A continuación, observarás un video de cómo este criterio se vincula con la resolución de un problema que se te puede presentar en la vida cotidiana.
- Aplicaciones de la semejanza de triángulos.
En el primer ejemplo: ¿Te diste cuenta cuál es la relación existente entre los elementos que se describieron en el problema y los que se mencionaron en los triángulos semejantes anteriores?
En el segundo ejemplo: Realiza un modelo similar al que los chicos hicieron en el video y el reto es que lo hagas en casa y lo pruebes calculando alguna altura que no puedas medir fácilmente. Y registra después sus datos y cálculos.
Anota tus conclusiones en tu cuaderno para tener evidencia de tu análisis.
A lo largo de la historia de las matemáticas te puedes encontrar con pasajes que involucran a personajes que nunca imaginaste que, de alguna manera, estuvieron inmersos en ellas.
A propósito, ¿Te acuerdas del nombre del personaje que se mencionó en el video anterior?, si te acuerdas anótalo en tu cuaderno.
Reflexiona con una presentación, que precisamente involucra a un personaje ya conocido.
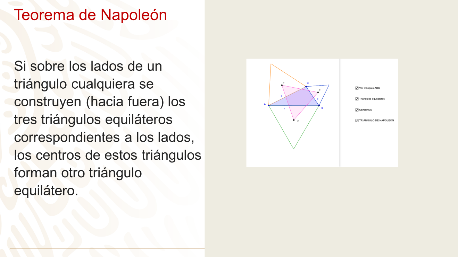
Hazlo paso por paso al trazarlo y así obtener, cual es la relación del tema con este teorema:
- Traza un triángulo cualquiera que se llamará ABC.
- Sobre cada lado del triángulo ABC, se trazan triángulos equiláteros.
- Localiza los centros de cada triángulo equilátero trazado, esto se logra trazando las 3 mediatrices o 3 medianas a cada triángulo equilátero, el punto de intersección son los centros DEF.
- Se unen los 3 centros DEF con segmentos de recta, formando otro triángulo equilátero, llamado DEF. Este es el Triángulo de Napoleón.
- Teorema de Napoleón. GeoGebra
https://www.geogebra.org/m/CfCuwvX7
Si tomas cualquiera de los vértices del triángulo original, A o B o C, y lo mueves en cualquier dirección, verás cómo al cambiar la forma del triángulo original, cambian los tamaños de los triángulos equiláteros y cambia el tamaño también del triángulo DEF, o sea el triángulo de Napoleón.
Observa bien el trazo obtenido y reflexiona, no es necesario que hagas cálculos.
Señala la respuesta correcta en cada pregunta:
- ¿Cómo son, El triángulo original ABC y los triángulos equiláteros de cada uno de los lados?
- Congruente
- Semejante
- Diferente
- ¿Cómo son los triángulos equiláteros de cada lado del triángulo ABC, con el triángulo de napoleón DEF?
- Congruente
- Semejante
- Diferente
Anota tus respuestas en tu cuaderno, reflexiona sobre ellas y compáralas con los ejercicios anteriores que resolviste y claro, compártelas para interactuar con tus compañeros.
El reto de hoy:
Seguro te preguntarás ¿Por qué triángulo de Napoleón? Ese es el reto, investígalo.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: