Sólidos de revolución – Aprende en Casa

Sólidos de revolución

Aprendizaje esperado: resuelve problemas que implican calcular el volumen de cilindros y conos o cualquiera de las variables que intervienen en las fórmulas que se utilicen. Anticipa cómo cambia el volumen al aumentar o disminuir alguna de las dimensiones.

Énfasis: estudiar los sólidos de revolución.

¿Qué vamos a aprender?

Los materiales que vas a necesitar en esta sesión es tu cuaderno, lápiz y goma.

La siguiente carta es de una alumna de tercero de secundaria. Su nombre es Romina y dice que hace un par de días vio un programa en televisión. En el cual una atleta de patinaje artístico sobre hielo realizaba giros con su cuerpo, apoyada en una sola pierna y flexionando la otra.

Romina escribió que, al ver a la patinadora realizar movimientos en distintas posiciones, logró formar en el aire algunos cuerpos geométricos. Tanta fue su impresión que consiguió una fotografía de una patinadora profesional y la envió junto con su carta.

Esa patinadora es toda una profesional. Flexionar así sus piernas no es nada sencillo.

Con mucho entrenamiento y disciplina se puede lograr.

Pero ¿qué es lo que más le impresiona a Romina del movimiento de la patinadora?

Las figuras que se forman durante su giro. Puedes imaginar a la patinadora cuando está girando, pero no se ven figuras.

Observa de nueva cuenta la fotografía:

Si girara hacia la derecha —utilizando como eje de rotación la punta de su pie—, ¿qué cuerpo geométrico generaría con su movimiento?

Si gira hacia la derecha. imagina Se formaría una esfera.

Al igual que tú, Romina se interesó mucho, e investigó algunas posiciones y movimientos básicos del patinaje artístico.

Hizo los trazos correspondientes para poder anticipar qué cuerpos se generan en el aire con los giros.

Estos son los trazos de Romina.

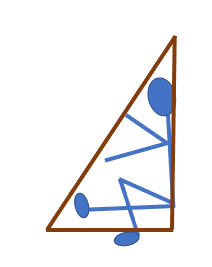
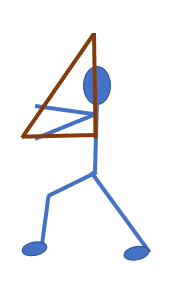
A B

Se observa que en el trazo A, la patinadora gira su cuerpo hacia la derecha, apoyada en una sola pierna y poniendo en posición horizontal la otra pierna. Romina visualiza que esa pierna horizontal —junto con los brazos y el cuerpo de la patinadora—, forman un triángulo rectángulo perfecto.

En los siguientes trazos, Romina dibujó tres diferentes posiciones, a las cuales se llaman posiciones C, D y E.

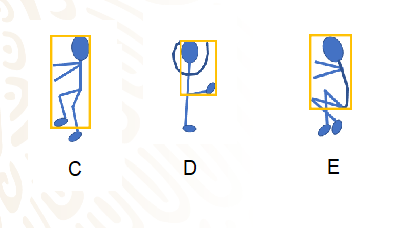
¿Qué figura geométrica trazó Romina sobre cada uno de los esquemas que representan a la patinadora?

Un rectángulo en cada una. A diferencia de los triángulos rectángulos que trazó en los esquemas A y B.

Dibuja sólo las figuras geométricas visualizadas en los esquemas A, B, C, D y E de los trazos de Romina.

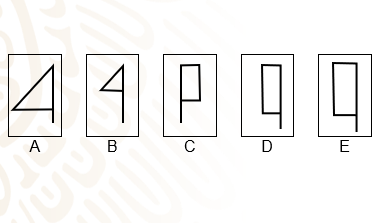
En estas figuras geométricas se nota que las figuras A y B corresponden a triángulos rectángulos, mientras que las figuras C, D y E a rectángulos.

Si estas figuras geométricas se hicieran girar en torno a su eje, ¿qué cuerpo geométrico se genera?

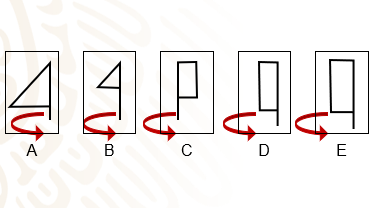
Si se giraran los primeros dos triángulos rectángulos, se conseguirían conos.

Y ¿qué cuerpo geométrico se forma al hacer girar cualquiera de los rectángulos sobre el eje que está dibujado?

Se forma una especie de tubo, es un, un cilindro

Con toda esta información, se realiza una tabla que contenga el trazo y el cuerpo geométrico que se consigue al girar sobre un eje.

La tabla incluye el cuerpo geométrico generado y su trazo correspondiente.

¿Qué cuerpo geométrico se genera al hacer girar sobre su propio eje a un triángulo rectángulo? Como los tipos A y B.

Se genera un cono.

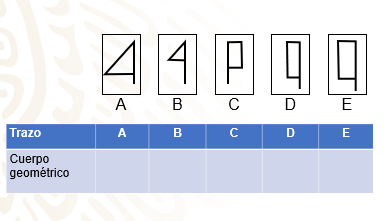
Y ¿qué cuerpo geométrico se genera al girar sobre uno de sus lados un rectángulo como los de las figuras C, D y E.

Un cilindro.

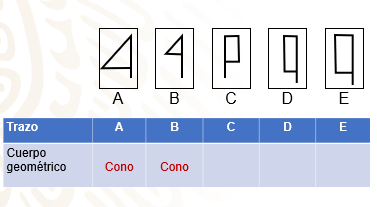
En cuanto a los trazos de los triángulos rectángulos A, B y C, generan un cono al girarlos.

Mientras que los trazos de los rectángulos C, D y E generan un cilindro al girarlos.

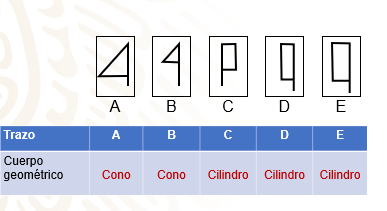
En el caso de los triángulos, es posible generar conos si los triángulos son de diferente tamaño, sin importar su tamaño.

Y de igual manera puedes cambiar la medida sin importar el tamaño de los rectángulos de la base como de la altura, y al girar, se genera un cilindro.

Valida si se forman los cuerpos que registraste en la tabla.

Para llevar a cabo esta actividad, se utiliza una hoja en blanco, un popote o un palito de madera, tijeras y cinta adhesiva.

En el papel. traza tres triángulos rectángulos como los de la siguiente imagen y con las medidas que se prefieras. Recorta los triángulos rectángulos para luego pegarlos al palito del lado del cateto a.

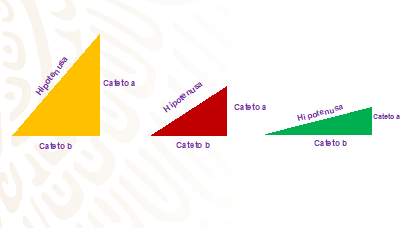
Se gira el palo al que se pegó cada triángulo rectángulo para comprobar lo siguiente:

¿se reconoce qué cuerpo geométrico se formó al girar cada triángulo rectángulo sobre su eje?

Observa cómo se genera el cono

Después, se registra en la tabla las características del cuerpo geométrico que se forma.

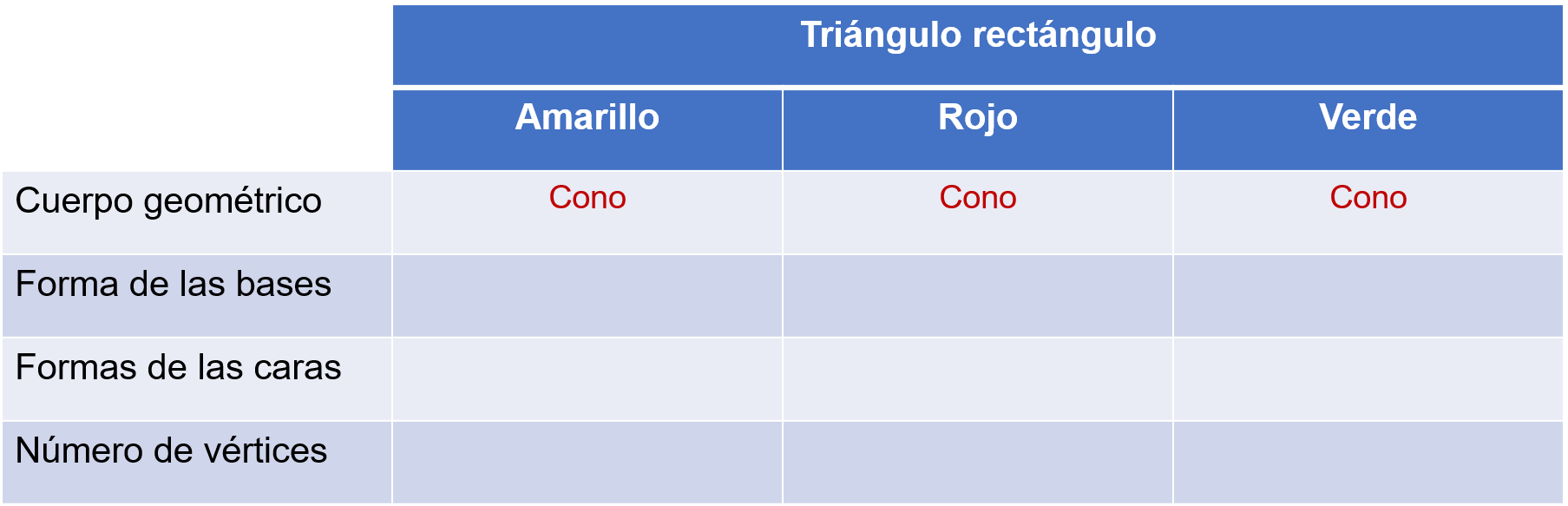
¿Qué cuerpo geométrico se generó al girar los triángulos rectángulos amarillo, rojo y verde sobre uno de sus catetos?

Un cono.

¿Y cuál es la forma de la base de cada cono generado?

Un círculo

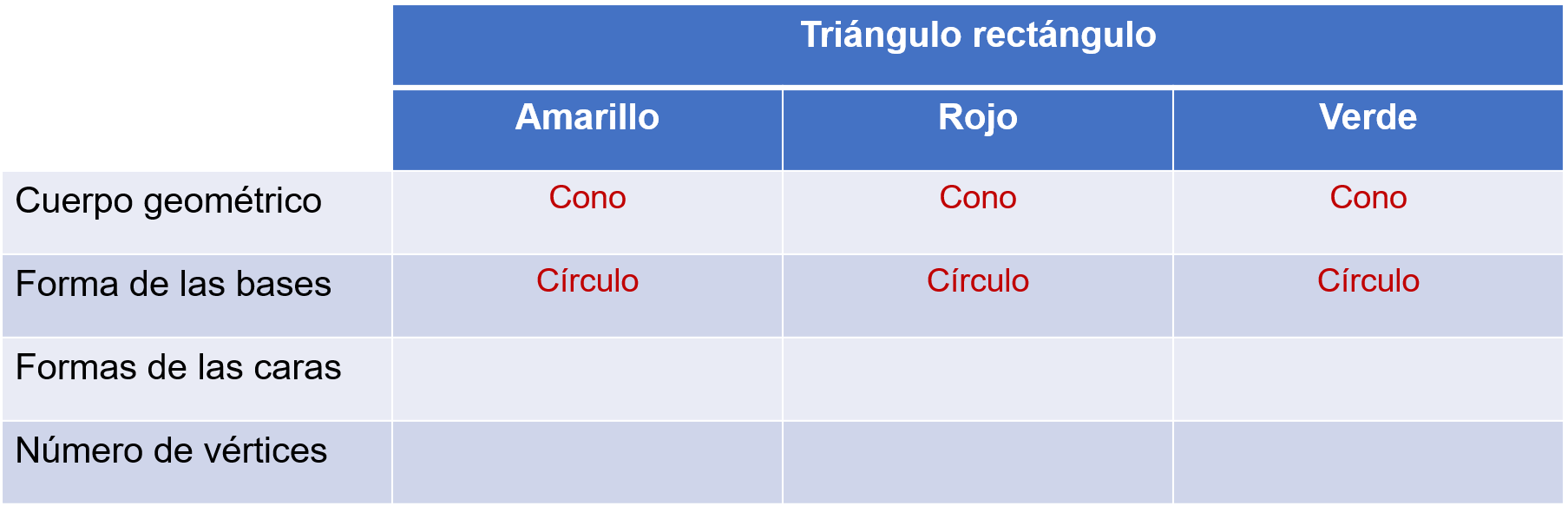
No tiene este cono caras laterales.

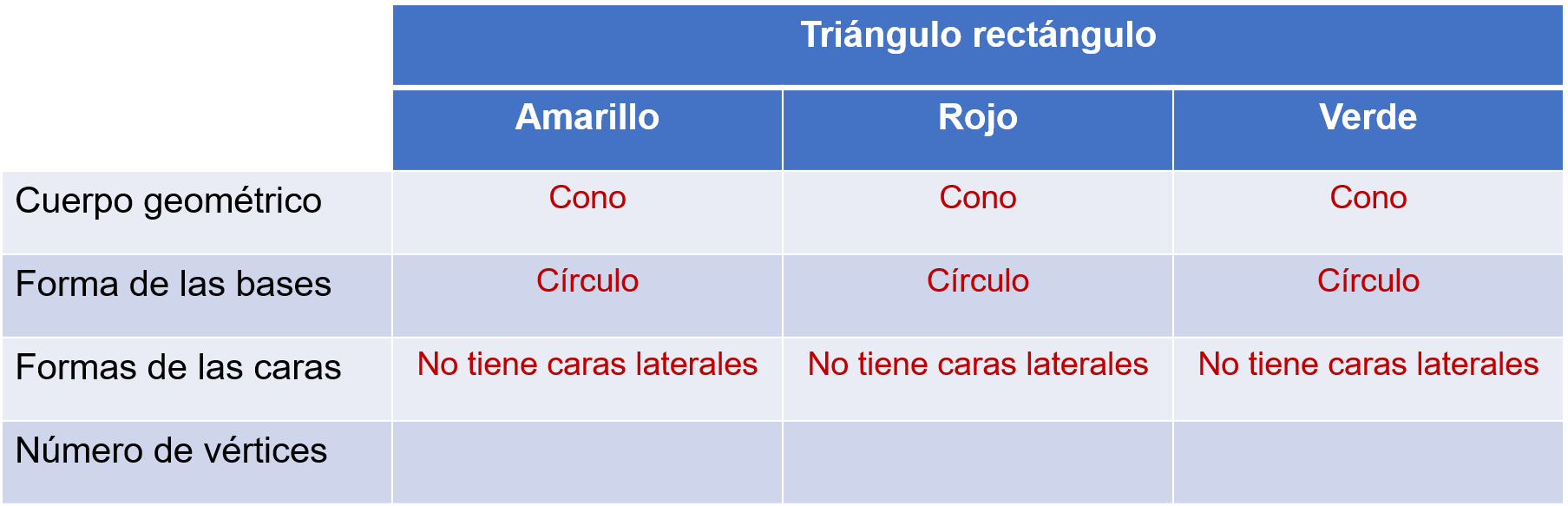
El cono tiene un solo vértice.

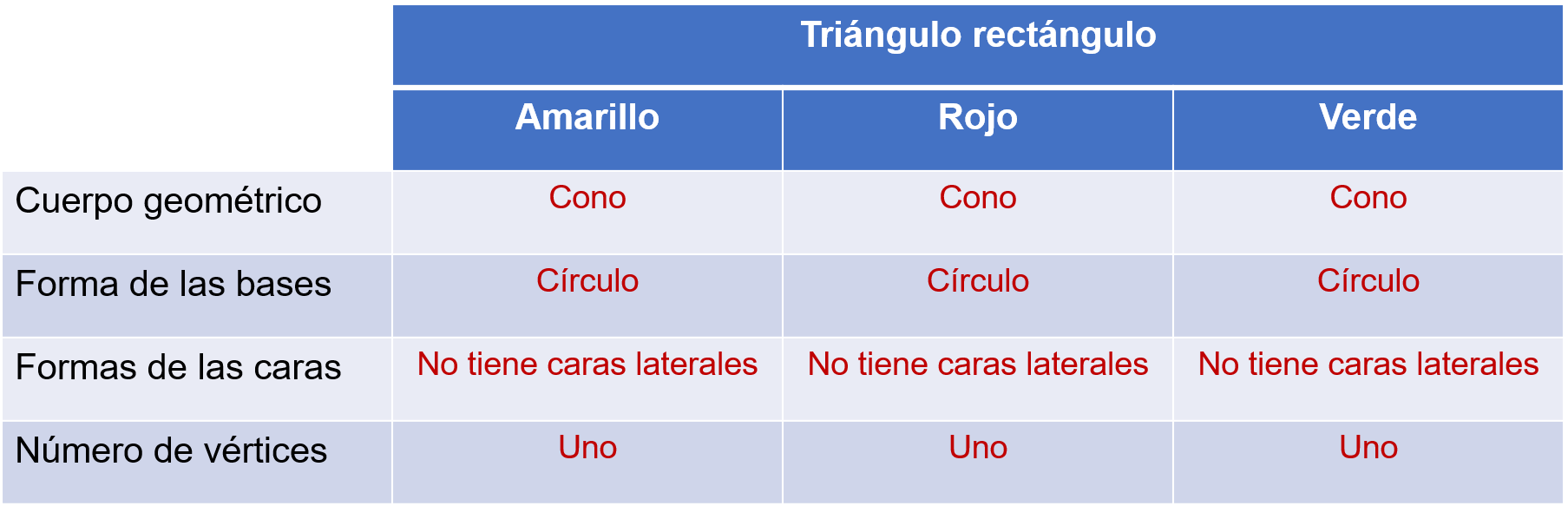
Es correcto afirmar que, al girar un triángulo rectángulo pegado a uno de sus catetos se forma un cono

Comprueba qué es lo que Romina imaginó al ver la fotografía de la patinadora.

En la fotografía original trazó un arco y en la copia, un semicírculo. Luego trazó un arco y una semicircunferencia en una hoja de papel, los recortó y pegó cada uno por el eje de cada figura a un popote para comenzar a girarlos.

El cuerpo geométrico obtuvo Romina con este movimiento para el arco fue un óvalo

Y el cuerpo geométrico que se generó al rotar la semicircunferencia fue una esfera.

¿Qué hacemos?

Registra en una tabla las características de los cuerpos geométricos generados.

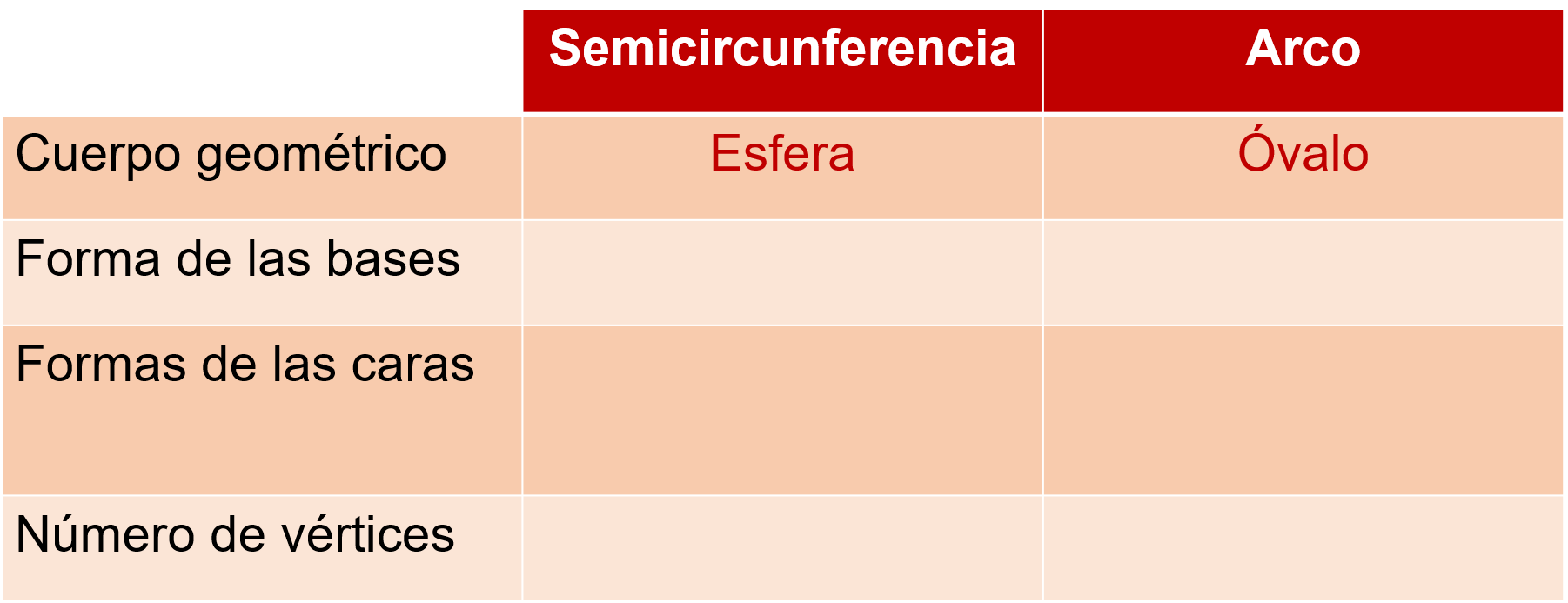
¿Cuál es la forma de la base, al girar tanto el arco como de la semicircunferencia?

Ninguna, porque no tienen base.

¿Cuál es la forma de las caras?

Tampoco tienen caras laterales.

¿Y qué se dice del número de vértices de cada figura generada?

Que ninguna de las dos tiene vértices.

Antes de continuar se concluye lo siguiente:

Un dato relevante: ¿sabías que a estos tres cuerpos geométricos se les llama sólidos de revolución?

Los cuerpos de revolución son aquellos sólidos que se obtienen al girar una figura plana alrededor de un eje de rotación. Es decir, son los cuerpos que se generan al rotar una región del plano alrededor de una recta.

El cilindro, el cono y la esfera son sólidos de revolución.

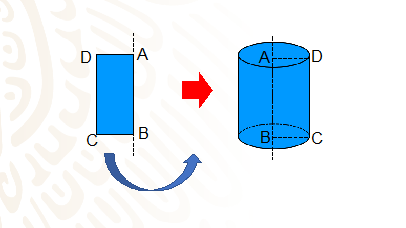
El cilindro es el cuerpo generado por un rectángulo que gira alrededor de uno de sus lados. En el esquema observa que el lado AB es el eje de giro o eje del cilindro, y es la altura del sólido.

El lado CD produce la superficie lateral del cilindro y se denomina generatriz.

Y de los lados AC y BD resultan dos círculos que son las bases del cilindro.

El cono se obtiene al girar un triángulo rectángulo alrededor de uno de sus catetos. El cateto fijo es el eje del cono, y la longitud de este cateto es la altura. La rotación del otro cateto genera un círculo perpendicular a la altura y corresponde a la base del cono; la longitud de esta base es el radio del cono. La hipotenusa del triángulo que se rota es la generatriz. El punto de intersección de la generatriz con el eje se llama vértice del cono.

La esfera se obtiene al girar un semicírculo alrededor de su diámetro.

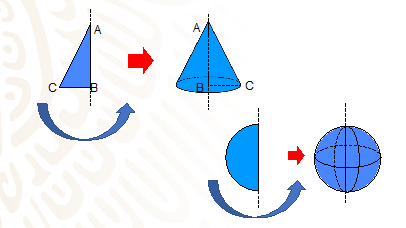
En los sólidos de revolución se llama generatriz a una línea puede ser recta, curva o una combinación de ambas, que al girar alrededor de otra recta llamada directriz, genera una forma geométrica conocida como sólido de revolución.

Y para entender estos conceptos, observa las siguientes figuras.

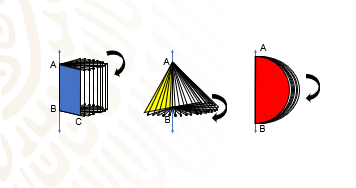
En estos ejemplos puedes observar que: el segmento DC en el rectángulo azul, el segmento AC en el triángulo amarillo y la línea curva AB del semicírculo rojo son todos ellos generatrices que al girar dan origen a un cilindro, un cono y una esfera.

Te puedes encontrar nuevas situaciones en las que se generen cuerpos de revolución. Por ejemplo:

Para hacer sus vasijas, un alfarero no sólo requiere la destreza de sus manos sino de la mezcla de barro y el torno.

Al girar el torno, el alfarero puede modelar la figura deseada con sus manos. En este caso:

¿qué figura está formándose al girar el barro? Te daré una pista: es un sólido de revolución.

La alfarería es una aplicación práctica de la que se consiguen sólidos de revolución a través de los giros sobre un eje determinado.

Otro ejemplo de la vida cotidiana está relacionado con una de las ceremonias de las culturas mesoamericanas: la ceremonia de Los Voladores, que se practica en algunas comunidades de los estados de Hidalgo, Puebla y Veracruz, aunque probablemente los más famosos sean Los Voladores de Papantla. ¿Los has visto alguna vez? A continuación, don Leopoldo hablará de esta práctica.

Cápsula Don Leopoldo y los voladores de Papantla
(del minuto 13:55 al minuto 15:00)
https://youtu.be/HiNHwWTiXKc
Pero ¿cómo se sabe cuáles son estos sólidos.?

Se señalan los puntos A, B y C, de tal manera que BC es perpendicular a AC. Suponiendo que la cuerda no aumenta su longitud y al dar una vuelta, ¿qué trayectoria sigue el punto B al girar?
La trayectoria que sigue el punto B es una trayectoria circular.
La forma geométrica que describe el segmento BC mientras el volador gira alrededor del poste es un círculo
¿Puedes localizar en la fotografía el triángulo formado por los puntos A, B y C?
¿El triángulo ABC?,¿ya lo identificaste?
El cuerpo geométrico que se obtiene cuando el triángulo ABC gira alrededor del poste se llama cono.
Los sólidos de revolución se encuentran en distintos lugares. Pero ¿se pueden generar sólidos de revolución sin hacer girar una figura plana en torno al eje directriz?
Ahora piensa en un cilindro. ¿Cómo puedes generarlo a partir de un círculo?
¿Un círculo que genera un cilindro?
¿Has visto esas bases que sirven para apilar discos compactos?
¿Qué sucede cuando sólo dejas un disco en el fondo de la base? Ese disco compacto tiene la forma de un círculo y si lo deslizas por todo el soporte si trasladas el disco en planos paralelos hasta llegar al tope del soporte, ¿cuál cuerpo geométrico se genera?

Se forma un cilindro.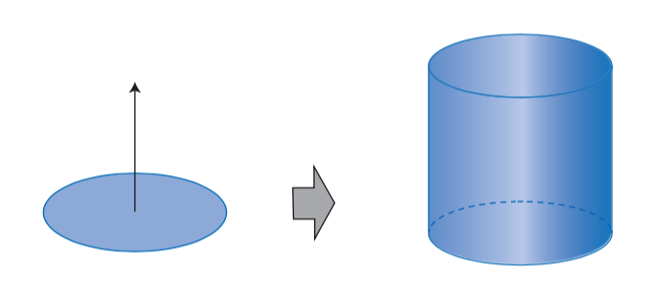

¿Has visto el espectáculo que algunas personas realizan con burbujas de jabón?
En un documental una persona explicaba cómo se forman esas grandes burbujas de jabón.
Para formar una gran burbuja adentro de otra, se eleva un aro de cincuenta centímetros de diámetro lleno de espuma a partir del piso y en posición horizontal. De ese modo, se forma una gran burbuja alrededor de esa persona.
Suponiendo que el movimiento del aro siempre está alineado al cuerpo de la persona, ¿cuál sólido se forma? Se forma un cilindro, un cilindro de jabón.

¿Y cuántas bases tiene ese cilindro? Tiene dos.
¿Se pueden generar conos y esferas con sólo trasladar una sección de esos sólidos de revolución?
Si trasladas la base de un cono hacia su vértice, no. No se genera un cono, se genera un cilindro. Si haces cualquier corte transversal a una esfera y ese corte lo trasladas a través del eje de simetría de la esfera, tampoco generas una esfera
No se pueden generar trasladando una sección transversal de un cono o de una esfera para formar el propio cono o esfera. Entonces, ¿qué sucede con el cilindro? ¿Acaso es especial?
El cilindro es un caso particular: se puede generar al hacer un movimiento de traslación de un círculo a lo largo de una recta perpendicular a la base, como en los dos ejemplos antes mencionados.
En esta sesión aprendiste que, a partir de figuras planas, como el triángulo rectángulo, el rectángulo y el círculo girando en torno a un eje, se generan los sólidos de revolución.
Observa “un dato por conocer”, traído por don Leopoldo, que subraya las 3 ideas que se aprendieron sobre los sólidos de revolución:
Cápsula 2: Don Leopoldo