Sistemas de dos ecuaciones lineales con dos incógnitas

Sistemas de dos ecuaciones lineales con dos incógnitas

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: interpretar el significado que tienen las incógnitas en ambas ecuaciones de un sistema.

¿Qué vamos a aprender?

Conocerás cómo representar algebraicamente los sistemas de ecuaciones lineales con dos incógnitas y los resolverás con el apoyo de tablas de datos o registros tabulares.

¿Qué hacemos?

De acuerdo con los conocimientos adquiridos anteriormente, reflexiona respecto a las siguientes preguntas:

¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

¿Qué necesita suceder para encontrar las soluciones de un sistema de ecuaciones lineales?

Si aún no conoces las respuestas, observa siguiente video, en el que se explican las principales características de los sistemas de ecuaciones lineales 2 x 2.

Ahora, aplica lo visto en el video y resuelve las siguientes situaciones. Toma nota de la información dada en cada problema, e intenta resolver lo que se plantea. A final, podrás validar tus resultados.

Nery juntó durante una semana varias monedas de $2 y de $5 que le dieron su mamá y su papá para gastar en la escuela o como gratificación al hacer compras en la tienda.

Cuando su prima Sofía le preguntó que cuánto dinero había juntado, Nery le lanzó el siguiente reto.

Para ello, observa la plática entre Nery y su prima Sofía.

Analiza la respuesta de Sofía. Considera que Nery juntó 15 monedas de $2 y de $5, que suman $48.

Presta atención a la siguiente imagen y comprueba si Sofia tenía razón.

La respuesta de Sofía no cumple con las condiciones del problema

¿Cómo se pueden calcular las monedas de cada denominación que juntó Nery?

Para obtener la respuesta, primero se representa algebraicamente la situación. Como son dos variables las que aparecen en el problema, las monedas de 2 pesos y las de 5 pesos, y dos condiciones; se puede representar con un sistema de ecuaciones lineales dos por dos.

Las condiciones del problema son:

Ya que cuentas con el sistema de ecuaciones, representa la información en una tabla de datos para resolver el problema.

Copia la tabla en tu cuaderno y complétala.

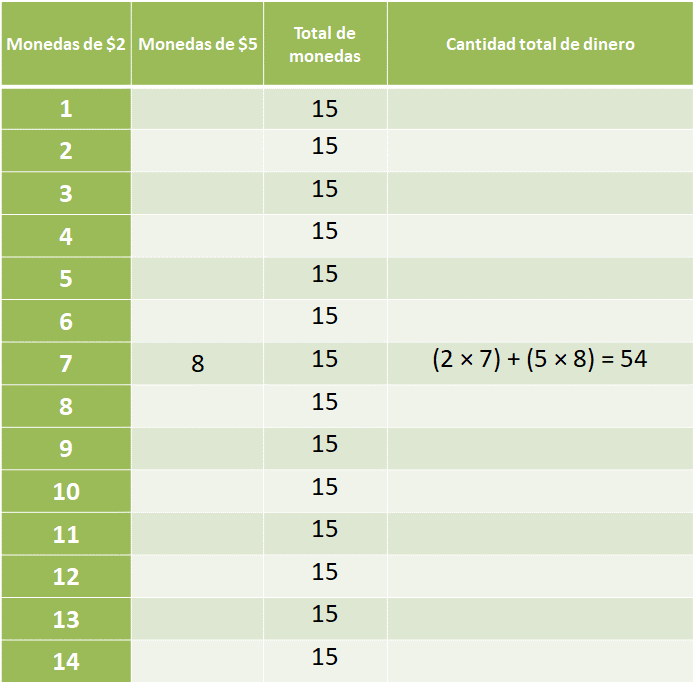
Considerando las monedas de dos pesos, y el total de monedas que tiene Nery, que son 15. Calcula las monedas de cinco pesos y la cantidad total de dinero que habría en cada caso representado en la tabla.

¿Cómo se obtienen los valores que faltan en la tabla de datos?

¿Qué tiene que suceder, en los valores de la tabla, para obtener las respuestas del problema?

En la tabla anterior s representó la respuesta que dio Sofía, siete monedas de 2 pesos más 8 monedas de 5 pesos que son igual a 54 pesos, y se corroboró que la respuesta no es correcta ya que: (7×2) + (5×8) = 54

Ahora, completa la tabla…

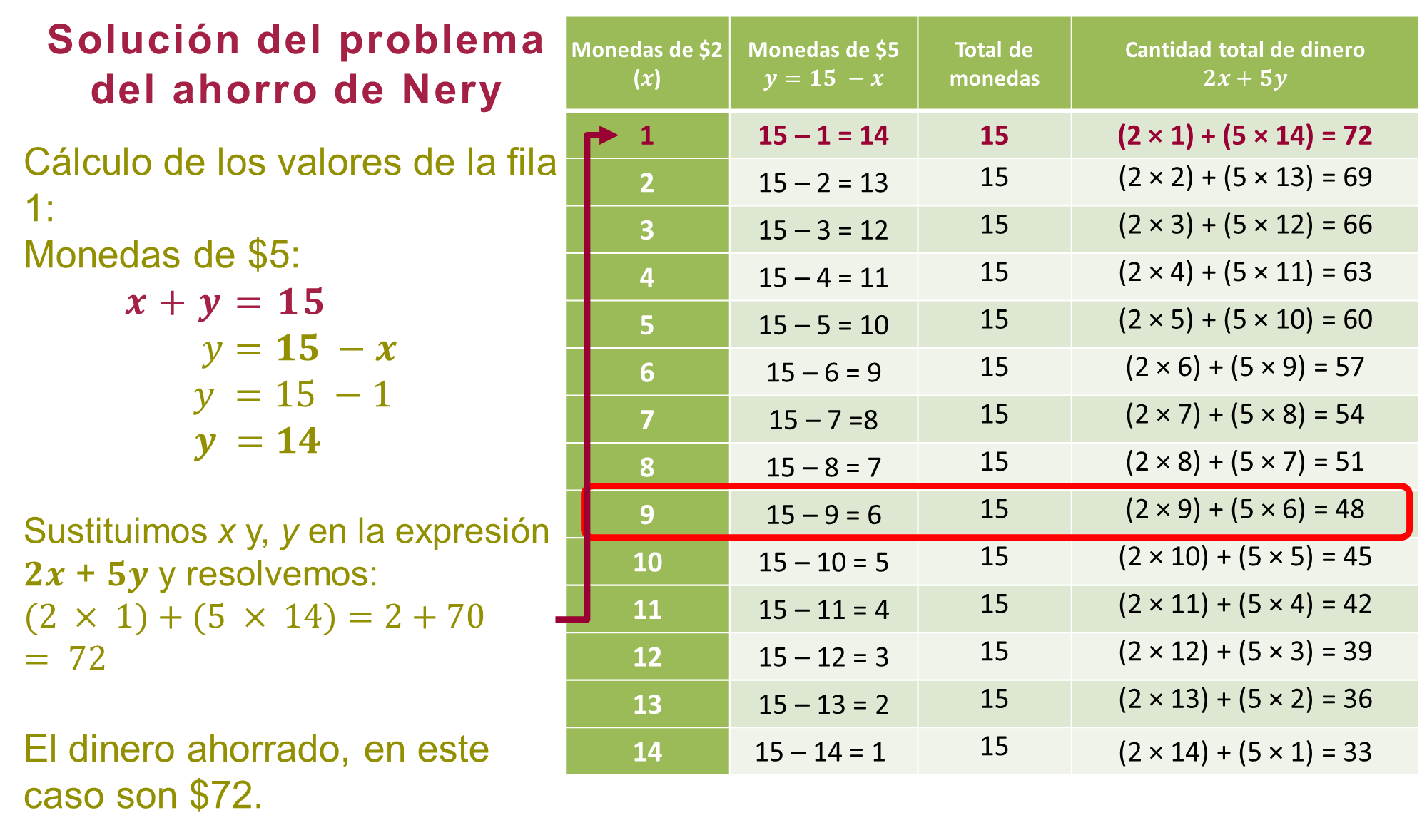
Para responder la pregunta:

¿Qué tiene que suceder, en los valores de la tabla, para obtener las respuestas del problema?

Se conoce que “x” más “y” deben sumar 15, entonces se asigna a “y” los valores correspondientes a los respectivos valores de x, que aparecen en la tabla para tener el total de monedas de 5 pesos, es decir, a 15 se le restan los valores de “x”.

Observa el ejemplo de la fila 1: se sabe que el total de monedas son 15, cantidad a la que se le resta 1, que es el número de monedas de 2 pesos, y con ello se obtiene la cantidad de monedas de 5 pesos; que en ese caso son 14. Es decir, x + y = 15, por lo tanto, “y” es igual a 15 menos equis, y al sustituir equis, se tiene que “y” es igual a 15 menos 1, lo que da el resultado de 14. Después, en la columna 4 se sustituyen “x” y “y” por los valores correspondientes para resolver la expresión 2x + 5y, es decir, por 1 y por 14, por lo tanto:

1 x 2 + 5 × 14 = 2 + 70 = 72

Es la cantidad de dinero que habría en este caso, es decir, son 72 pesos.

De la misma manera se completan todas las filas de la tabla, sustituyendo a “x” y a “y” por los valores correspondientes, como pueden ver.

Observa con detenimiento la tabla:

¿En qué columna los valores de “x” y “y”, es decir, el número de monedas de $2 y de $5, cumplen con las dos condiciones del problema?

En la tabla se puede observar que 9 monedas de 2 pesos y 6 monedas de 5 pesos suman 15 monedas y corresponden a los 48 pesos que juntó Nery.

Porque: 2 x 9 + 5 × 6 = 18 + 30 = 48 pesos.

Has resuelto el sistema de ecuaciones, ahora, comprueba si esto es cierto.

Para comprobar lo anterior, plantea nuevamente la pregunta de Nery:

En total junté 15 monedas que suman 48 pesos. ¿Cuántas monedas tengo de cada denominación?

Sustituye a “x” y a “y” por los valores numéricos obtenidos y resuelve las operaciones.

Como sabes que:

x = 9

y = 6

Entonces, en la ecuación x + y = 15, al sustituir a las incógnitas queda 9 + 6 = 15, llegando a 15 igual que 15, esto significa que la igualdad es verdadera.

Y en el caso de la segunda ecuación: 2x + 5y = 48, al sustituir a las incógnitas, queda 2(9) + 5(6) = 48, esto es 18 + 30 = 48, llegando a 48 igual que 48, esto significa que la igualdad es verdadera.

Has comprobado que los valores encontrados de “x” y “y”, satisfacen o hacen verdaderas las ecuaciones que forman el sistema propuesto para resolver el problema, cumpliendo las condiciones que comentó Nery.

Para fortalecer tus conocimientos, resuelve el siguiente caso.

El equipo de futbol de Néstor

Néstor juega en un equipo de futbol. En esta temporada han tenido un excelente inicio de torneo, pues se mantienen invictos después de jugar los primeros 12 partidos, es decir no han perdido un solo juego, sin embargo, también se sabe que no han ganado todos los partidos, pues algunos han empatado.

Antes de resolver el problema, recuerda que en el futbol las victorias o partidos ganados otorgan tres puntos y que los empates, solamente un punto.

Para responder la pregunta de Néstor, se planteará el sistema de ecuaciones correspondiente y se resolverá con el apoyo de una tabla de datos.

Ya que tienes el sistema de ecuaciones lineales que corresponde al problema, se representa la información en una tabla de datos. No olvides copiar la tabla en tu cuaderno y completarla, de acuerdo con lo que se indica en la siguiente imagen.

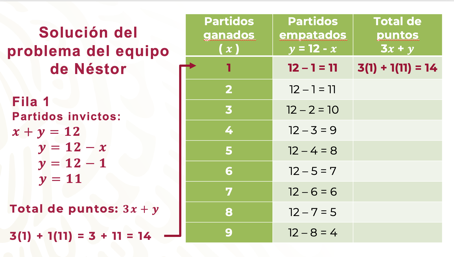
“x” más “y” deben sumar 12, entonces se asignan a “y” los valores correspondientes a los respectivos valores de x, que aparecen en la tabla para tener el total de partidos, es decir, a 12 le se le restan los valores de “x”.

Después, se resuelve la expresión 3x + y, para obtener el total de puntos, en cada caso, como muestra el ejemplo de la primera fila de la tabla. En este caso, se puede ver que 12 – 1 = 11, que cumple con la primera condición del problema, es decir, con el número de partidos invictos, pero el total de puntos: (3 x 1) + (1 x 11) = 14, no cumple con la segunda condición del problema, es decir, con el total de puntos del equipo.

¿Cuántos partidos ganó y cuántos partidos empató el equipo de Néstor?

Observa la tabla completa para validar tus resultados.

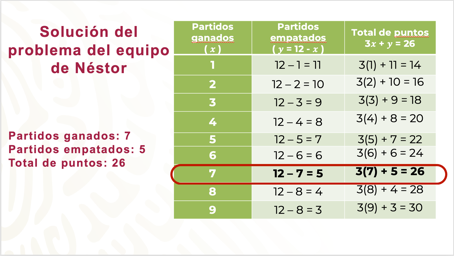
Observa la tabla de datos con detenimiento. Como puedes ver, si el equipo de Néstor hubiera ganado 2 partidos y empatado 10, se tendría: 3 x 2 + 10 = 6 + 10 = 16 puntos; si hubieran ganado 3 partidos y empatado 9, se tendrían 18 puntos, para 4 partidos ganados y 8 empatados, sus puntos serían 20, y así sucesivamente.

Los valores de “x” y de “y” que cumplen con las dos condiciones del problema son: “x” igual a siete y “y” igual a cinco: partidos ganados 7, partidos empatados 5 y total de puntos 26.

Para comprobar las soluciones del problema, se sustituyen ambas literales por su valor numérico, en ambas ecuaciones y se resuelven las operaciones:

Partidos invictos:

x + y = 12 es igual a 7 + 5 = 12

Se cumple la igualdad porque 12 es igual que 12.

Puntos obtenidos:

3x + y = 26 es igual a 3 × 7 + 5 = 21 + 5 = 26

Como 26 es igual que 26, se cumple la segunda igualdad.

Néstor dice: Ganamos 7 partidos y empatamos 5.

Al resolver las operaciones se comprueba que las respuestas que encontraste en la tabla son correctas.

Ahora reflexiona:

¿Qué situación de tu vida diaria, familiar o escolar piensas que pueda ser representada, y resuelta, por medio de un sistema de ecuaciones lineales 2 x 2?

A continuación, analiza el siguiente sistema de ecuaciones 2×2, y piensa en una situación que pueda ser representada con dicho sistema.

Recuerda que el sistema de ecuaciones es:

x + y = 45

x + 7 = y

Observa el siguiente ejemplo que representa al sistema:

Carlos tiene en una bodega 45 cajas de dos tipos de frutas, unas son de mangos y las otras de peras. También se sabe que tiene 7 cajas más de peras que de mangos.

¿Cuántas cajas tiene de cada tipo de fruta?

Si usa “x” para representar las cajas de mangos y “y” para las cajas de peras. Se puede ver que la información del problema planteado corresponde al sistema de ecuaciones. Ahora, se cambia de lenguaje algebraico al lenguaje común, como puedes ver.

Después, se representa la información en una tabla de datos para resolver el problema. Recuerda copiar la tabla y completarla en tu cuaderno.

“x” más “y” deben sumar 45, entonces se asignan a “y” los valores correspondientes a los respectivos valores de x, que aparecen en la tabla para tener el total de cajas, es decir, a 45 se le restan los valores de “x”.

Se asignan diferentes valores a “x”, en este caso, serán entre 16 y 22 cajas, también se anota en cada fila el total de cajas que tiene Carlos, que es 45, y se buscan los valores de “y” que, sumados a los respectivos valores de x, den 45. En la fila 1, se puede ver que, “y” es igual a 45 – 16 = 29.

Para completar la tabla sigue el mismo procedimiento en cada fila.

Al completar la tabla, podrás ver que en todas las filas se cumple con la primera condición o ecuación del problema, que es x + y = 45.

Ahora, tienes que buscar la fila en la que los valores de “x” y de “y” cumplan con la segunda condición o ecuación, x + 7 sea igual a “y”, es decir, que “y” sea 7 unidades mayor a x.

¿Ya sabes cuáles son estos valores?

¿Cuántas cajas de mangos y cuántas de peras tiene Carlos?

Observa la siguiente tabla para verificar tus resultados.

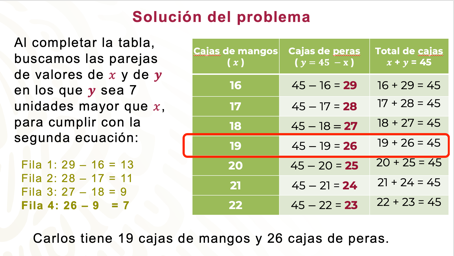
Después de completar la tabla, busca las parejas de valores de “x” y de “y” en los que “y” sea 7 unidades mayor que x, para cumplir con la segunda ecuación.

Ahora sabes que “x” vale 19 y que “y” vale 26. Es decir, Carlos tiene 19 cajas de mangos y 26 cajas de peras.

Nuevamente comprueba las soluciones del sistema, sustituyendo a las incógnitas por sus valores numéricos y resolviendo las operaciones.

El sistema de ecuaciones es:

Has terminado con la representación y resolución del Sistema de Ecuaciones Lineales 2 por 2, con el apoyo de tablas de datos.

Recuerda que puedes consultar tu libro de texto de Matemáticas 2, para buscar información que permita resolver tus dudas o para poner en práctica lo estudiado en esta sesión.

El reto de hoy:

La siguiente imagen muestra la gráfica de uno de los sistemas de ecuaciones que resolviste, corresponde al problema del equipo de futbol de Néstor.

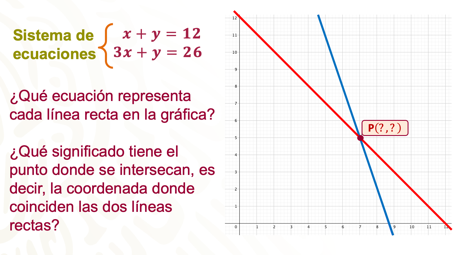
Analiza las relaciones entre “x” y “y” de cada línea recta. Cada una corresponde a una de las ecuaciones del sistema.

Y responde lo siguiente:

¿Qué ecuación representa cada línea recta en la gráfica?

¿Qué significado tiene el punto donde se intersecan, es decir, la coordenada donde coinciden las dos líneas rectas?

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/