Sistema de ecuaciones. Método gráfico
Sistema de ecuaciones. Método gráfico
Aprendizaje esperado: resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.
Énfasis: resolver problemas que implican un sistema de ecuaciones lineales utilizando el método gráfico.
¿Qué vamos a aprender?
Los materiales que necesitarás son tu cuaderno de apuntes, bolígrafo, lápiz, goma, regla o escuadra y lápices de colores.
Anteriormente, trabajaste con el estudio de sistemas de ecuaciones lineales, resueltos por diversos métodos: El de sustitución, igualación y reducción.
Para esta sesión se resuelven problemas de sistemas de ecuaciones lineales con dos incógnitas a través del método gráfico. Es decir, analizando el comportamiento de las rectas que se obtienen en el plano cartesiano según la solución del sistema.
¿Qué hacemos?
Los sistemas de ecuaciones pueden tener una solución única, no tener solución o tener un número infinito de soluciones.
Con certeza de lo anterior, se inicia con un ejercicio que plantea una profesora a sus alumnos de secundaria.

Con esta información, se plantea el sistema de ecuaciones pertinente.
Se asigna “x” para las monedas de 2 pesos y “y” para las monedas de 5 pesos.

En el monedero se tiene un total de $55 pesos entre monedas de 2 y 5 pesos.
La suma total del dinero es equivalente al valor nominal de la moneda por el número de monedas. De este modo, el total de dinero en monedas de 2 pesos es 2 por “x”, mientras que el total en dinero que se tiene con las monedas de 5 pesos se representa como 5 por “y”. Es así como la primera ecuación es “2x” más “5y” igual a 55.
Y la segunda ecuación expresa que, son 20 monedas en total. Por lo tanto, la ecuación es “x” más “y” igual a 20.
Con las ecuaciones planteadas, se resuelve el sistema por el método gráfico. Pero primero, se necesita saber cómo hacerlo.
Primero, se despeja “y” de ambas ecuaciones:
Para la primera ecuación, “2x” más “5y” igual a 55 se resta “2x” en ambos miembros de la ecuación.
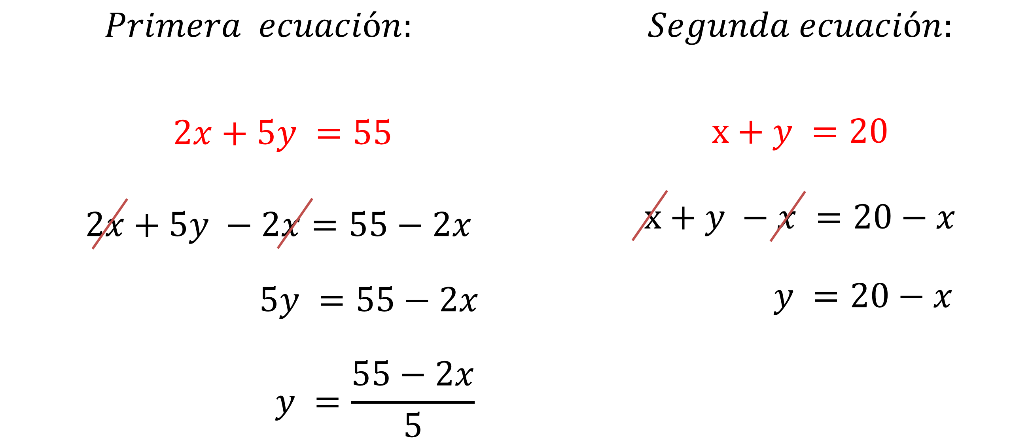
En consecuencia, “2x” más “5y” menos “2x” igual a 55 menos “2x”. Se cancelan términos y se tiene que “5y” es igual a 55 menos “2x”, y se dividen entre 5 ambos miembros, quedando “y” igual a 55 menos “2x”, todo entre 5.
Para la segunda ecuación, “x” más “y” igual a 20, se resta “x” de ambos miembros y se tiene:
“x” más “y” menos “x” es igual a 20 menos “x”.
Se cancelan términos, y se tiene “y” igual a 20 menos “x”.
Con las ecuaciones despejadas, se elabora una tabla por ecuación dando valores a “x”, y así obtener pares ordenados que se grafican en el plano cartesiano.
Con lo anterior, se usan 3 coordenadas para trazar cada una de las rectas. Se sabe que geométricamente con dos puntos es suficiente para determinar una línea recta, así que se emplea un tercer punto como apoyo, y se asignan los valores para “x” igual a 10 negativo, 0 y 10.
Para la expresión “y” igual a 55 menos “2x” todo entre 5.
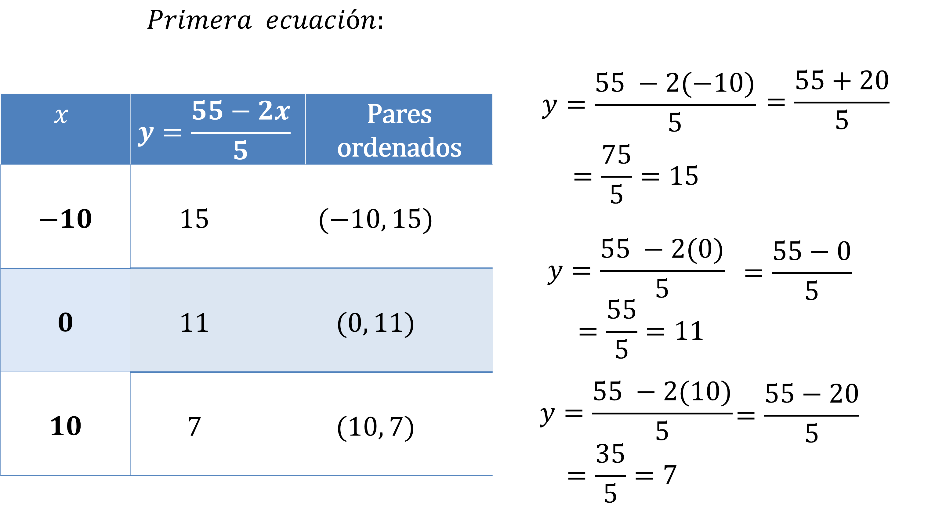
Mientras que “x” igual a 10 negativo, “y” es igual a 55 menos 2 por 10 negativo, todo entre 5, igual a 55 más 20, todo entre 5, es igual a 75 entre 5, igual a 15.
Asimismo, “x” igual a cero, “y” igual a 55 menos 2 por cero, todo entre 5, es igual a 55 menos cero entre 5, que es igual a 11.
Y para “x” igual a 10, “y” igual a 55 menos 2 por 10 todo entre 5, igual a 55 menos 20 todo entre 5, igual a 35 entre 5, que es igual a 7.
En la expresión “y” igual a 20 menos “x”.

Para “x” igual a 10 negativo, “y” es igual a 20 menos 10 negativo, igual a 20 más 10, igual a 30.
Para “x” igual a 0, “y” igual a 20 menos cero, igual a 20.
Para “x” igual a 10, “y” igual a 20 menos 10, igual a 10.
Se ubican en el plano cartesiano las coordenadas por las que pasan ambas rectas: Para la primera, se localiza (-10,15), (0,11) y (10,7).
Para la segunda, se localizan (-10, 30), (0, 20) y (10, 10), y se identifica el punto de intersección de estas, que corresponden a (15, 5).
Se te sugiere utilizar un color distinto para cada una de éstas y marcar el punto.
Es así como se tiene que, la solución del problema es la coordenada (15, 5). Ya sabes que cada coordenada en el plano cartesiano es un par ordenado (x,y), en donde “x” es igual a 15 y “y” es 5. De este modo, ambos números son la solución del sistema de ecuaciones.
Por lo tanto, la solución al problema es:
15 monedas de $2 pesos y 5 monedas de $5 pesos.
Si se comprueban los resultados en el sistema de ecuaciones, se tiene que:
La primera ecuación es “2x” más “5y” igual a 55, y si se sustituyen los valores se tiene: 2 por 15, más 5 por 5, es igual a 30 más 25 que es igual 55.

55 es igual a 55, y se mantiene la igualdad en la primera ecuación.
Mientras que para la segunda ecuación se tiene “x” más “y” igual a 20; se sustituyen los valores y 15 más 5 es igual a 20; 20 es igual a 20.
Por lo tanto, la solución se demuestra como correcta al cumplirse las dos igualdades.
Revisa los pasos a seguir para solucionar un sistema de ecuaciones por el método gráfico. A continuación, se describen:

Analiza el siguiente ejercicio que lo plantea un compañero de secundaria del Estado de México.
- Audio de Luis Rodrigo

Con las dos pistas, se plantean las ecuaciones que representan el problema:
Se asigna a “x” como el número de vacas, y a “y” como el número de chivos.
De la pista 1 se tiene que “x” (número de vacas) más “y” (número de chivos) es igual a 12 animales.
De la pista 2 se tiene que el número de chivos “y” es igual al triple del número de vacas, es decir “3x”.

Dada la información, se despeja “y” en ambas ecuaciones
De la ecuación 1, se tiene que “x” más “y” es igual a 12; para despejar a “y” se resta “x” de ambos miembros y se cancelan términos, dejando como resultado “y” es igual a 12 menos “x”.
Mientras que para la ecuación 2, ya está despejada la “y” que es igual a “3x”.
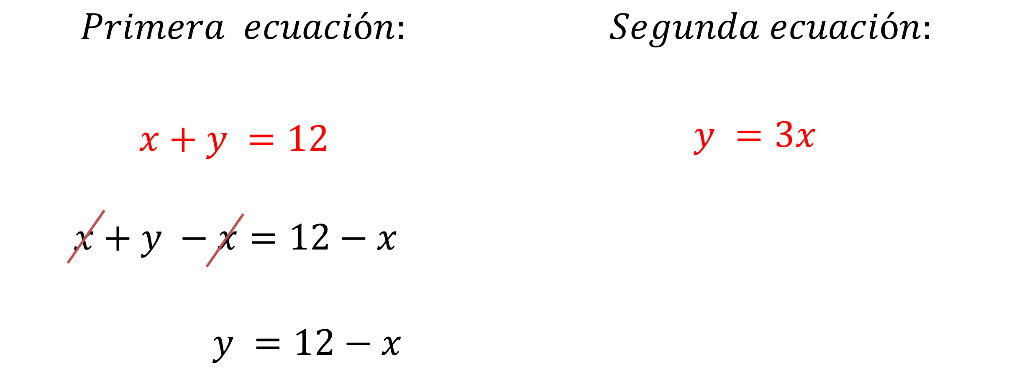
Se asigna a “x” los valores de 10 negativo, cero y 10 para ambas ecuaciones y la tabla correspondiente.
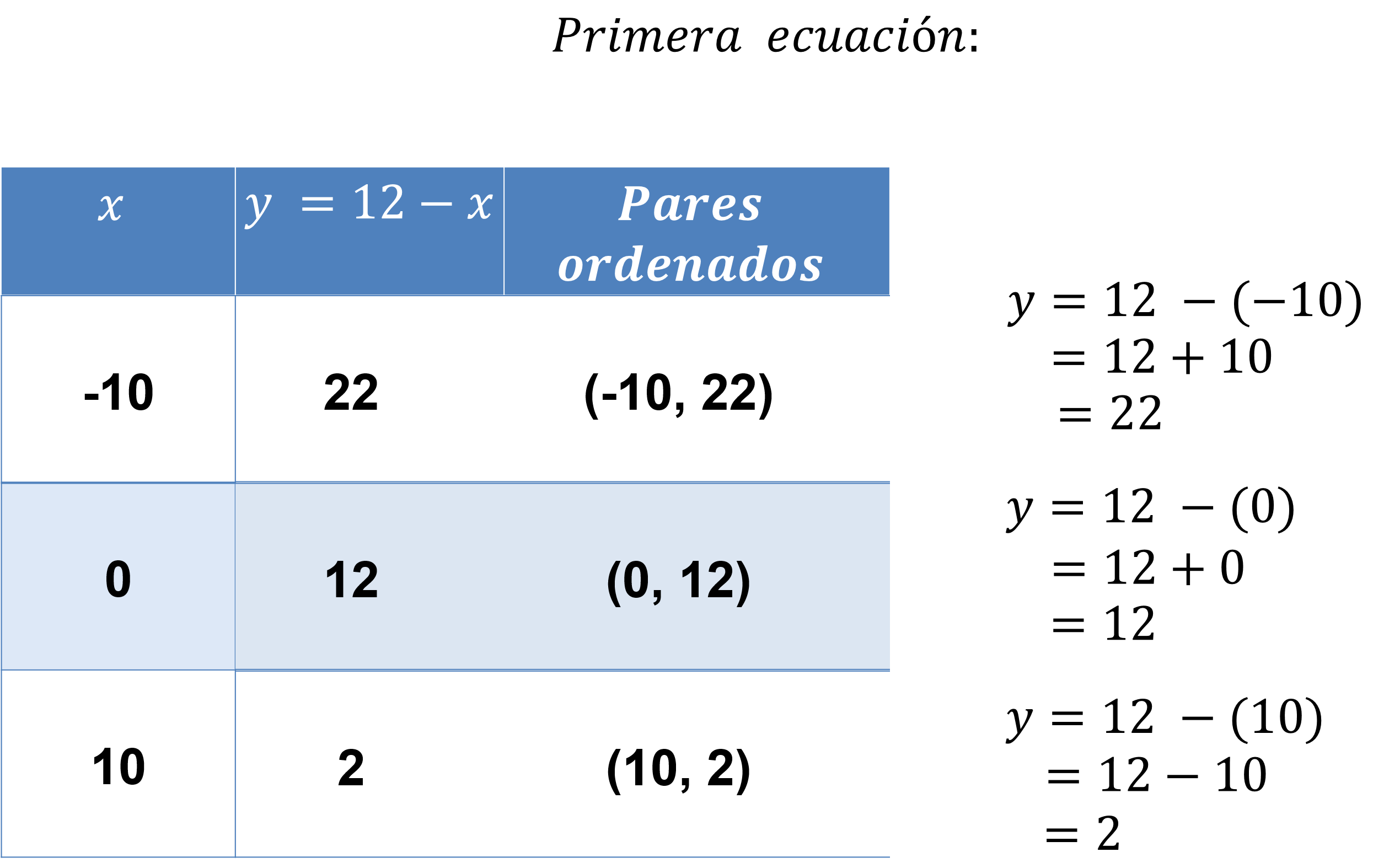
De la primera ecuación, “y” igual a 12 menos “x”,
Para “x”, igual a 10 negativo, “y” es igual a 12 menos 10 negativo, igual a 12 más 10 igual a 22.
Para “x” igual a 0, “y” igual a 12 menos 0 igual a 12.
Para “x” igual a 10, “y” igual a 12 menos 10 igual a 2.
Y para la segunda ecuación.
Se tiene que “y” es igual a “3x”.
Para “x” igual a 10 negativo, “y” es igual a 3 por 10 negativo igual a 30 negativo.
Para “x” igual a cero, “y” es igual a 3 por 0 igual a 0.
Para “x” igual a 10, “y” es igual a 3 por 10 igual a 30.

Después, se localizan las coordenadas en el plano cartesiano para formar las rectas.
Se ubica en el plano cartesiano las coordenadas por las que pasan ambas rectas:
Para la primera se localiza (-10,22), (0,12) y (10,2)
Para la segunda se localiza (-10,30), (0,0) y (10, 30)
Como podrás darte cuenta no se observa con claridad el valor del punto de intersección de las rectas.
Para esto, se realiza un acercamiento al plano cartesiano. En consecuencia, ya se observa que el punto de intersección de ambas rectas está en la coordenada (3,9). De este modo, “x” es igual a 3 y “y” igual a 9.
Ahora se sabe que el papá de Luis Rodrigo tiene 3 vacas y 9 chivos.
Y para comprarlo se sustituyen estos valores en las dos ecuaciones del sistema.
La primera ecuación es “x” más “y” igual a 12; se sustituyen los valores 3 más 9 es igual a 12, que es el total de animales.
La segunda ecuación es “y” igual a “3x”; cuando se sustituyen los valores 9 es igual a 3 por 3, por lo tanto, la igualdad es verdadera.

Y para asimilar el aprendizaje realiza otro ejercicio:
Supón que la trayectoria de dos barcos está modelada por las expresiones “2x” más “y” igual 5; y “4x” más “2y” igual a 10. ¿En qué punto del plano se encontrarán los dos barcos?
Para este ejercicio ya se tienen las ecuaciones dadas, por lo tanto, se despeja directamente la variable “y”.
Para la primera ecuación “2x” más “y” igual a 5, se resta de ambos miembros “2x” y se tiene “2x” más “y” menos “2x” igual a 5 menos “2x”; se cancelan términos y “y” es igual 5 menos “2x”.
La segunda ecuación es “4x” más “2y” igual a 10; para despejar “y”, se resta “4x” en ambos miembros y se tiene que “4x” más “2y” menos “4x” es igual a 10 menos “4x”; se cancelan términos y “2y” es igual a 10 menos “4x”.
Y, por último, se divide entre 2 ambos miembros y se tiene “2y” entre 2 es igual a 10 menos “4x” entre 2; se cancelan términos y “y” es igual a 10 menos “4x” entre 2.
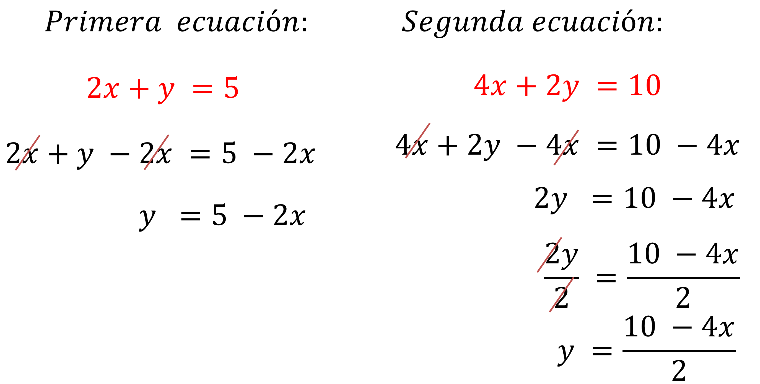
En consecuencia, corresponde tabular.
Para la primera tabla “y” igual a 5 menos “2x”.
Se sustituyen los valores para “x” igual a 10 negativo, cero y 10.
Para “x” igual a 10 negativo, “y” es igual a 5 menos 2 por 10 negativo, igual a 5 más 20, igual a 25.
Para “x” igual a 0, “y” es igual a 5 menos 2 por 0, igual a 5 menos 0, igual a 5.
Y para “x” igual a 10, “y” es igual a 5 menos 2 por 10, igual a 5 menos 20, igual a 15 negativo.

En la segunda tabla se emplean los mismos valores: Para la expresión “y” igual a 10 menos “4x” entre 2.
Para “x” igual a 10 negativo, “y” es igual a 10 menos 4 por 10 negativo entre 2, que es igual a 10 más 40 todo entre 2, igual a 50 entre 2, igual a 25.
Para “x” igual a 0, “y” es igual a 10 menos 4 por 0 entre 2, igual a 10 menos 0 todo entre 2, igual a 10 entre 2, igual a 5.
Y, por último, para “x” igual a 10, “y” es igual a 10 menos 4 por 10 todo entre 2, igual a 10 menos 40 todo entre 2, igual a 30 negativo entre 2, igual a 15 negativo.

Antes de graficar, al analizar las tablas se observa que los valores son iguales en las dos tablas, aunque las ecuaciones son diferentes. Además, se reconoce en la segunda ecuación que “y” es igual a 10 menos “4x” entre 2; si se simplifica “y” es igual a 5 menos “2x”.
Se puede afirmar que las ecuaciones son equivalentes y es la razón por la que los valores son iguales.
Hecha la aclaración, se sigue a graficar las expresiones que en este momento funcionan como funciones:
Se ubican los puntos en el plano cartesiano: (-10, 25), (0, 5) y (10, -15), y se traza la recta que representa a “y” igual a 10 menos “4x” entre 2.
Para la segunda expresión, “y” igual a 5 menos “2x”, se traza con otro color la recta coincidiendo con la anterior.
Si ambas rectas coinciden, ¿cuál es el punto solución del sistema de ecuaciones?
El método gráfico permite observar con claridad que, si todos los puntos coinciden, hay un número infinito de soluciones, ya que cada par ordenado de una de las rectas le pertenece a la otra.
Así, un sistema de ecuaciones formado por ecuaciones equivalentes tiene un número infinito de soluciones.
Pero regresando al ejercicio, al tener la misma ruta marítima, los barcos no pueden navegar al mismo tiempo y su programación debe ser distinta.
Analiza el último ejercicio planteado en un libro de texto de secundaria que propone lo siguiente:

Lo primero es plantear las ecuaciones. Se considera a “x” como el primer número y a “y” como el segundo número
La primera ecuación que representa “al triple de un número” menos “otro número” es igual a 4, es decir, “3x” menos “y” igual a 4.
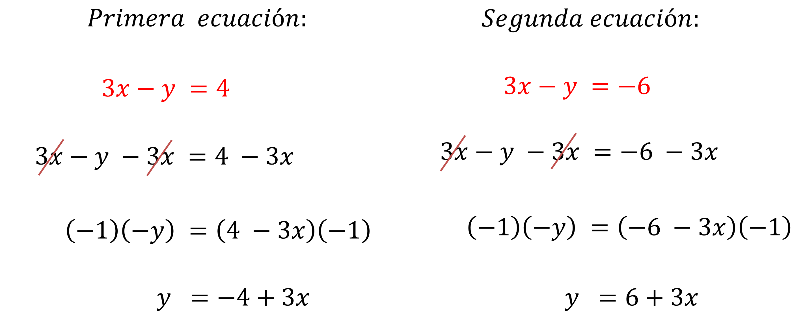
Para despejar, se resta “3x” en ambos miembros, obteniendo “3x” menos “y” menos “3x”, igual a 4 menos “3x” que es igual a “y” negativa, igual a 4 menos “3x”.
Como “y” es negativa, se multiplica toda la ecuación por 1 negativo; así “y” es igual a 4 negativo más “3x”.
En la segunda ecuación se tiene que “el triple de un número” menos “otro número” es igual a 6 unidades negativas, es decir, “3x” menos “y” es igual a 6 negativo.
Al despejar se resta “3x” en ambos miembros. Así “3x” menos “y” menos “3x” es igual a 6 negativo menos “3x”, que es igual a “y” negativa igual a 6 negativo menos “3x”. Por ser negativa la “y” se multiplica la ecuación por 1 negativo, y resulta en “y” es igual a 6 más 3x.
Y ya con la variable despejada, se realizan las tablas
Se utilizan para “x” los valores de 5 negativo, cero y 5.

En la primera tabla donde “y” es igual a 4 negativo más “3x”; para “x” igual 5 negativo, “y” es igual a 4 negativo más 3 por 5 negativo, es igual a 4 negativo más 15 negativo igual a 19 negativo.
Para “x” igual a 0, se tiene “y” es igual a 4 negativo más 3 por 0, es igual a 4 negativo más 0, igual a 4 negativo.
Para “x” igual a 5, “y” es igual a 4 negativo más 3 por 5, igual a 4 negativo más 15, igual a 11.
En la segunda tabla, se tiene la expresión “y” es igual a 6 más 3x.

Para “x” igual a 5 negativo, “y” es igual a 6 más 3 por 5 negativo, igual a 6 menos 15, igual a 9 negativo.
Para “x” igual a 0, “y” es igual a 6 más 3 por 0, es igual a 6 más 0, igual a 6.
Para “x” igual a 5, “y” es igual a 6 más 3 por 5, igual a 6 más 15, igual a 21.
Ya con las tablas se puede graficar en el plano cartesiano
Se ubica en el plano cartesiano las coordenadas por las que pasan ambas rectas:
Para la primera se localizan los puntos (-5,-19), (0,-4) y (5,11).
Para la segunda se localizan los puntos (-5,-9), (0,6) y (5, 21).
Al analizar, se observa que las rectas no se cortan en ningún punto, ya que tienen la misma pendiente que es (3) y, por lo tanto, son rectas paralelas.
Pero ¿qué significa este tipo de comportamiento?
Con esta gráfica se da lugar al último comportamiento de las rectas que forman un sistema de ecuaciones.
Al no existir un punto en donde se corten las rectas el sistema, no se tiene solución.
Entonces, para la conclusión se presentan las tres posibles soluciones de un sistema de ecuaciones observado a través del método gráfico.
Cuando las rectas que representan a las funciones asociadas a sus ecuaciones del sistema, en el plano cartesiano:
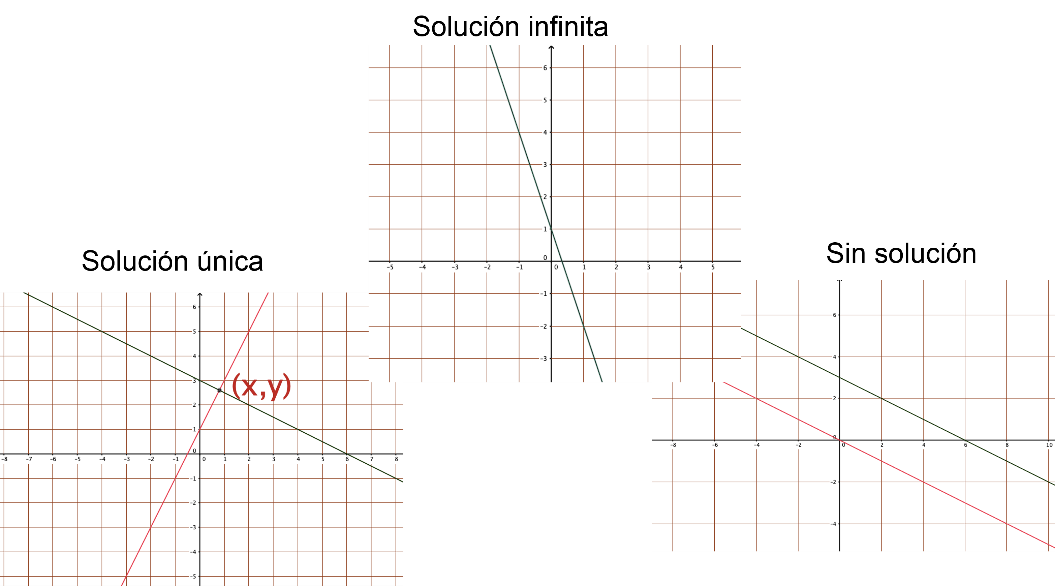
- Se cortan en un punto, la coordenada de ese punto (x, y) muestra los valores de las incógnitas. Ese es el punto solución.
- Las rectas coinciden en todos sus puntos, el sistema de ecuaciones tiene un número infinito de soluciones.
Y cuando las rectas son paralelas, el sistema de ecuaciones no tiene solución.
El reto de hoy:
Resuelve un sistema de ecuaciones por diversos métodos y así comprobar que se obtiene el mismo resultado.
Busca en tu libro de texto todo lo relacionado con el tema y resuelve los ejercicios que ahí se proponen para que puedas enriquecer tu conocimiento.
¡Buen trabajo!
Gracias por tu esfuerzo.