Sistema de ecuaciones: diversos métodos
Sistema de ecuaciones: diversos métodos
Aprendizaje esperado: resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.
Énfasis: aplicar varios procedimientos para resolver problemas que involucren sistemas de ecuaciones lineales.
¿Qué vamos a aprender?
Los materiales que necesitarás son tu cuaderno de apuntes, lápiz y goma.
Anota lo que consideres importante durante la sesión y no pierdas detalle de la información. Esto te permite llevar un orden en las actividades y retomar los temas con mayor claridad.
Hasta el momento te has planteado y resuelto problemas que implican sistemas de dos ecuaciones con dos incógnitas. Has utilizado los métodos de sustitución, igualación, reducción y método gráfico.
Por lo tanto, se deben activar los conocimientos previos sobre los sistemas de ecuaciones y así fortalecer lo que se está por conocer.
¿Qué hacemos?
Un sistema de dos ecuaciones lineales con dos incógnitas es: dos ecuaciones de primer grado, cuyos valores para cada incógnita satisfacen simultáneamente a ambas ecuaciones. Es decir, hacen verdaderas ambas igualdades, por ejemplo: “x” más “y” igual a 3, y “x” menos “y” igual a 1.
La solución al sistema de ecuaciones dado es: “x” igual a 2 y “y” igual a 1, porque al sustituir ambos valores y efectuar las operaciones indicadas, las dos igualdades son verdaderas.
2 más 1 igual a 3, y 2 menos 1 es igual a 1.

Resuelve la siguiente situación:
En el taller de Leonardo hay 43 vehículos para trabajo entre bicicletas y triciclos. Si el número total de ruedas es de 102, ¿cuántas bicicletas y triciclos hay?

Los pasos por seguir para resolver el problema son:
- Leer y comprender el problema, es decir, identificar los datos conocidos y las incógnitas.
En este caso, se conocen el número total de ruedas, 102, y el número total de vehículos, 43.
Mientras que las incógnitas son: el número de bicicletas y el número de triciclos.
Tras completar lo anterior se sigue con el paso 2: plantear un sistema de ecuaciones que represente el problema.
Para plantear las ecuaciones, cada uno de los datos desconocidos se representa con una literal:
El número de bicicletas se representa con la literal “x” y el número de triciclos con la literal “y”.

Posteriormente, se debe pensar en la expresión algebraica que representa la suma de la cantidad de bicicletas, más la cantidad de triciclos, igual a 43.

De este modo, si “x” representa el número de bicicletas y “y” el número de triciclos, que tras sumarse es 43, la ecuación queda:
“x” más “y” igual a 43.
Pero se debe considerar que, como lo indican en su nombre, las bicicletas tienen dos ruedas y los triciclos tres ruedas.
¿Cuál es la expresión algebraica que representa la suma del total de las ruedas, igual a 102?
La respuesta es: “2x” más “3y” igual a 102. Es así como las dos ecuaciones obtenidas son el sistema de ecuaciones lineales para dar solución al problema.
Pero queda por realizar el tercer paso: resolver el sistema de ecuaciones por uno de los cuatro métodos.
El primero de los métodos es el “método de reducción”, también llamado “suma y resta” porque consiste en multiplicar las ecuaciones del sistema por ciertos números, de tal manera que los coeficientes de alguna de las dos incógnitas sean simétricos. Esto, con el propósito de sumar o restar las ecuaciones y obtener una ecuación con una sola incógnita.
Los números simétricos son aquellos que tienen el mismo valor absoluto, pero con signo contrario. Por ejemplo: 5 y 5 negativo son simétricos.
Al sumar 5 más 5 negativo es igual a 0.
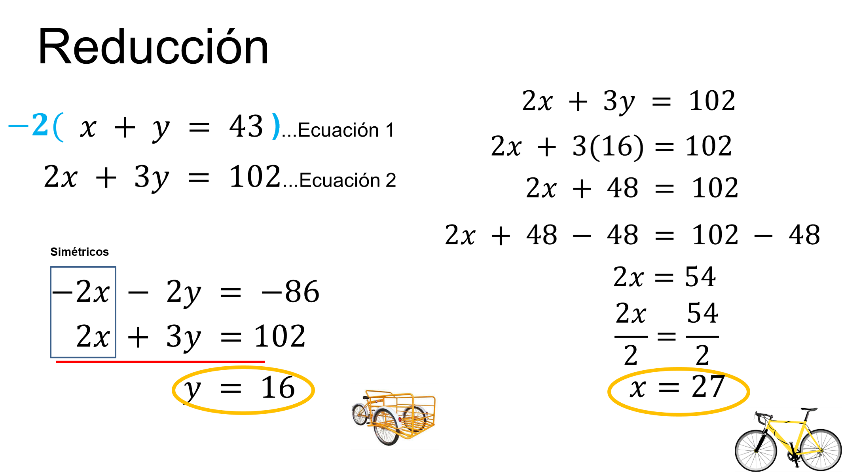
Para hacer simétricos los términos de “x”, se multiplica la primera ecuación por 2 negativo.
“x” más “y” igual a 43 por (2 negativo), igual a 2x negativo, menos “2y”, igual a 86 negativo.
Y de las dos ecuaciones, la segunda se conserva igual.
En el nuevo sistema de ecuaciones, se suman las dos ecuaciones y se obtiene una ecuación de primer grado con una incógnita: “y” igual a 16.
Como la “y” representa el número de triciclos, ya se sabe que hay 16 triciclos.
Y para determinar el valor de “x”, se sustituye el valor de “y” en cualquiera de las dos ecuaciones. En este caso, en la segunda ecuación.
“2x” más 3 por 16, igual a 102; al realizar las operaciones se tiene:
“2x” más 48 es igual a 102.
En ambos miembros de la ecuación se resta 48 y se obtiene “2x” igual a 54.
Se dividen ambos miembros de la ecuación entre 2, y el resultado es: “x” igual a 27.
En conclusión, se tienen 16 triciclos y 27 bicicletas.
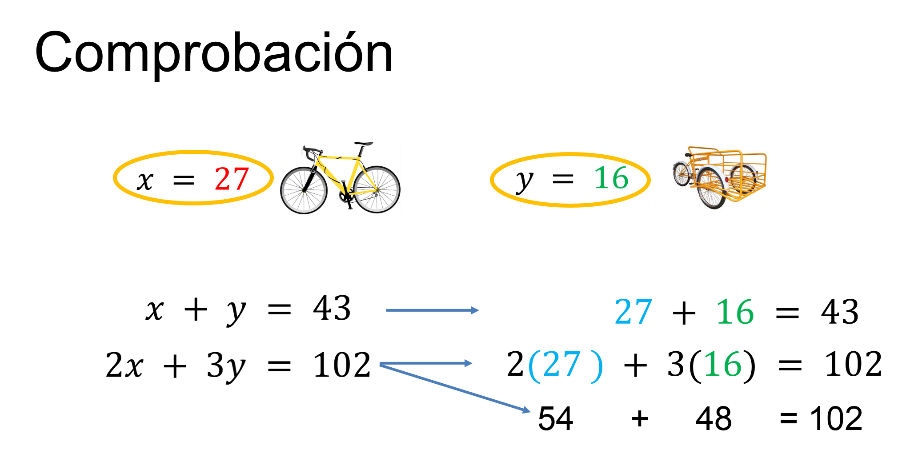
Para comprobar los valores encontrados se sustituyen los valores de “x” y “y” en las ecuaciones originales para verificar que se cumplan las igualdades.
En la primera ecuación, “x” más “y” igual a 43, se sustituye el valor de “x” por 27 y el valor de “y” por 16, igual a 27 más 16, igual a 43. Para esta ecuación, sí se cumple la igualdad.
Al sustituir en la segunda ecuación, se tiene 2 por 27, más 3 por 16, igual a 102. Al sumar 54 más 48 se obtiene 102. Del mismo modo, se cumple con la igualdad.
Por lo tanto, los valores encontrados “x” igual a 27, y “y” igual a 16, constituyen la solución al sistema de ecuaciones.
Por otra parte, el procedimiento para resolver el sistema de ecuaciones de primer grado con dos incógnitas con el “método de sustitución” es el siguiente:
Se elige una de las dos ecuaciones y se despeja una incógnita. Por ejemplo, en la ecuación 1 se despeja “x” igual a 43 menos “y”.
Se sustituye el valor algebraico de “x” en la segunda ecuación; se efectúan las operaciones correspondientes y se reducen términos semejantes que resultan en: 86 más “y” igual a 102.
En ambos miembros de la igualdad se resta 86 y se obtiene “y” igual a 16.

El valor encontrado de “y” se sustituye en cualquiera de las dos ecuaciones, pero se recomienda sustituir en la incógnita despejada.
Es decir, “x” igual a 43 menos 16; al realizar la resta “x” es igual a 27.
Como se demostró con el “método de sustitución”, son los mismos resultados que con el “método de reducción”: 16 triciclos y 27 bicicletas. Por ello, para este caso no es necesaria la comprobación.
Otro método para resolver una ecuación es a través de la igualación. En éste se despeja la misma incógnita en ambas ecuaciones para igualar las dos expresiones. Es así como se forma una ecuación de primer grado con una incógnita.
Se hacen las operaciones necesarias y se obtiene el valor de la incógnita, como se muestra a continuación.
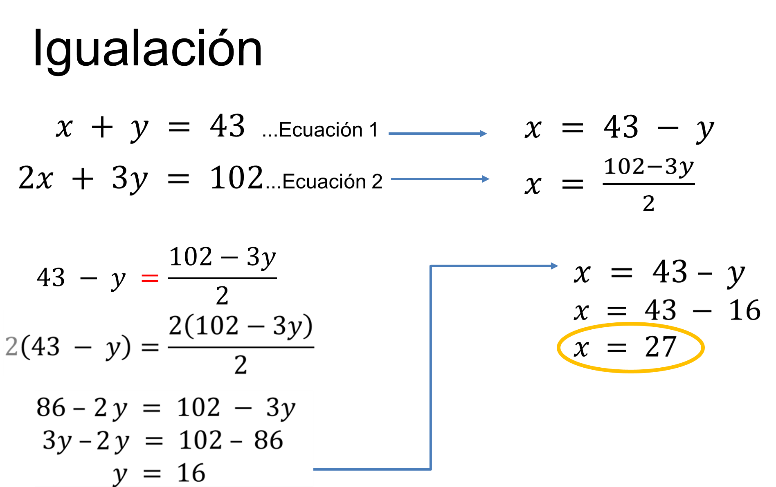
Se despeja “x” en ambas ecuaciones.
En la primera ecuación, a través del “método de sustitución” se obtuvo: “x” igual a 43 menos “y”.
En la segunda ecuación, se tiene “x” igual a 102 menos “3y”; todo dividido entre 2.
Y se igualan los dos valores de “x”:
43 menos “y” igual a 102, menos “3y” entre 2.
Y para resolver la ecuación, primero se multiplica por 2 ambos miembros de la igualdad y se obtiene: 86 menos “y” igual a 102 menos “3y”.
Se simplifica y el valor de “y” es igual a 16.
Para determinar el valor de “x” se sustituye el valor numérico de “y” en cualquiera de las dos ecuaciones originales, o bien, se puede sustituir en algunos de los valores donde despejas a “x”.
En este caso, se sustituye en el despeje de “x” igual a 43 menos “y”; entonces, se tiene “x” igual a 43 menos 16. Por lo tanto, el valor de “x” es igual a 27.
Si observas los valores encontrados, ¿cómo son respecto a los obtenidos en los métodos de reducción y de sustitución?
Se comprobó que son iguales. Hay 16 triciclos y 27 bicicletas.
Finalmente, se resuelve el mismo caso con “el método gráfico”, en donde la solución a un sistema de ecuaciones se representa por el punto en el plano cartesiano donde se interseca la recta de cada función asociada a la ecuación.
En este método siempre se despeja “y” en ambas ecuaciones:
En la primera ecuación, “y” es igual a 43 menos “x”.
Y en la segunda ecuación, “y” es igual a 102 menos “2x”, todo entre 3.
Se elabora una tabla de valores para cada expresión despejada, y se otorgan valores arbitrarios a “x” para obtener su correspondiente valor en “y”.
De este modo, con los valores de cada tabla se forman parejas ordenadas y se ubican en el plano cartesiano para trazar las gráficas.
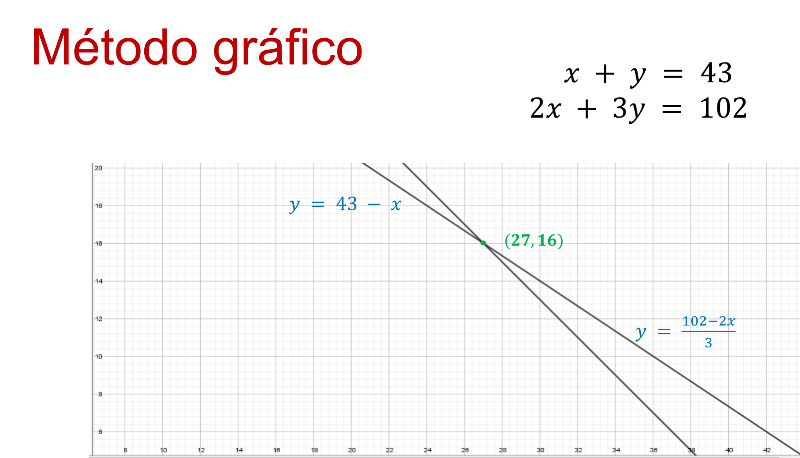
Al trazar las dos gráficas, una para cada ecuación, se localiza el punto en donde se intersecan ambas.
Este punto es la solución al sistema que indica el valor de “x” y “y”.
En ambas gráficas se identifica que el punto de intersección es 27 coma 16, es decir, “x” tiene el valor de 27 y “y” el valor de 16.
Por lo tanto, se tienen 27 bicicletas y 16 triciclos.
En algunas ocasiones, es posible encontrar de una manera sencilla los resultados por el método gráfico antes de trazar las gráficas.
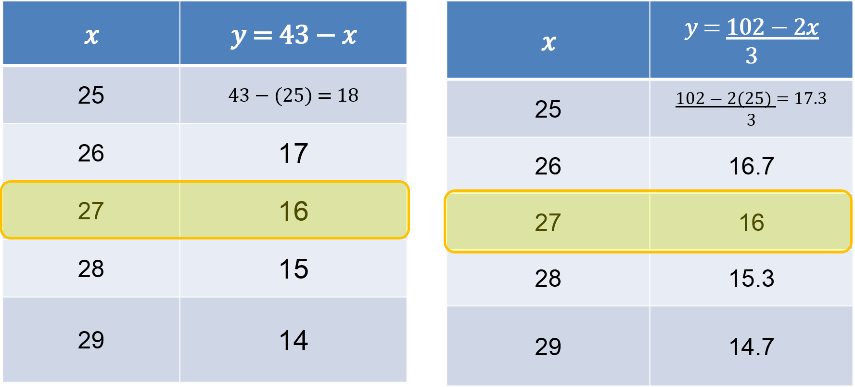
Esto se traduce al observar los valores de cada tabla, y ubicar las parejas ordenadas iguales en ambas.
Para este caso en ambas tablas, cuando “x” es 27, “y” tiene el valor de 16. Por lo tanto, esa es la solución del sistema de ecuaciones.
Como se ha demostrado, un mismo problema se resolvió por los cuatro métodos: reducción, sustitución, igualación y gráfico.
En cada método se obtuvo como resultado: que en el taller había 27 bicicletas y 16 triciclos.

Aunque en cada método el valor de las incógnitas resultó ser el mismo, en algunos el procedimiento es más largo; esto depende de las ecuaciones del sistema.
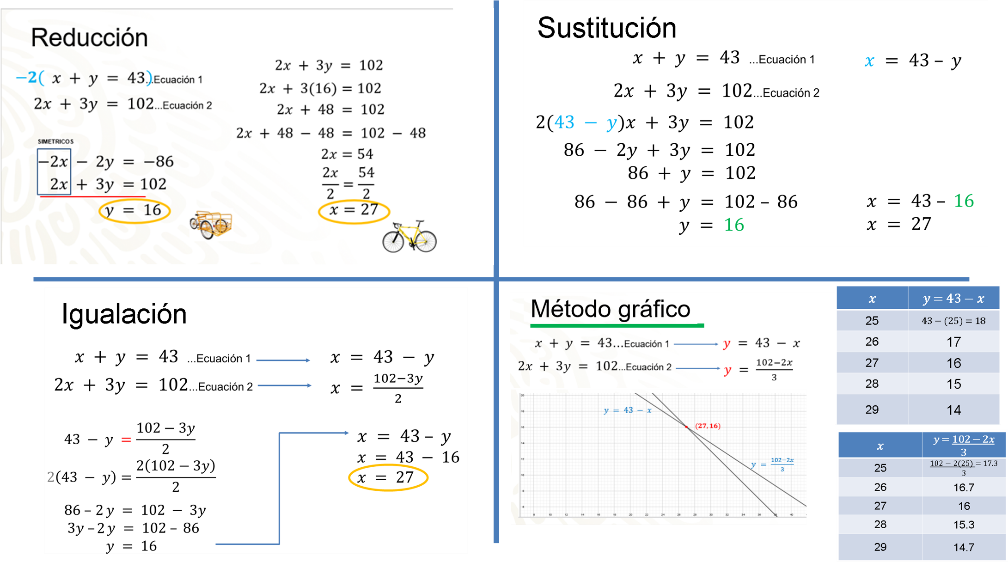
A veces pareciera más directo usar el “método de sustitución”, por mencionar un ejemplo; pero en otras ocasiones, como se muestra en la imagen, este método puede resultar más laborioso.
A partir de lo antes expuesto, reflexiona: ¿qué ventajas y desventajas existen de los 4 métodos revisados para resolver un sistema de ecuaciones?
Para dar respuesta, se debe de observar en qué casos es más recomendable un método que otro.
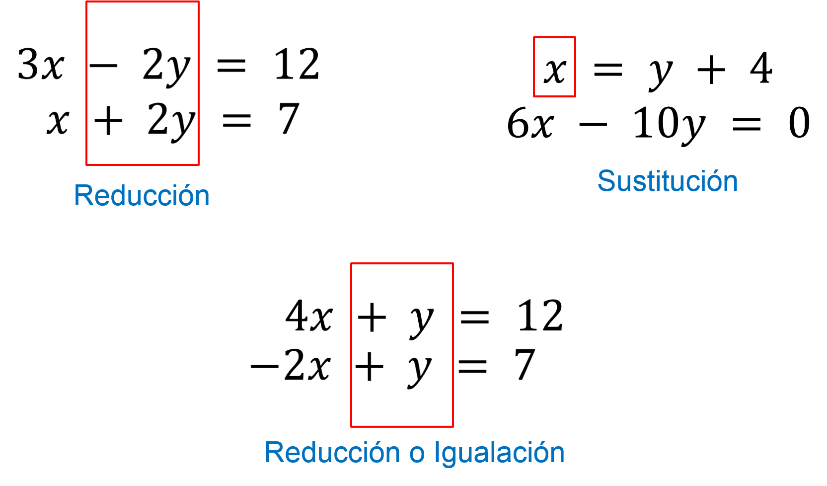
Con ese propósito se analizan los siguientes sistemas de ecuaciones para conocer las preferencias por usar un método u otro.
En el primer sistema de ecuaciones es notable que los coeficientes de la incógnita “y” son simétricos. Es decir, tienen el mismo valor absoluto, pero con signo contrario. Por ello conviene resolverse por el “método de reducción”, pues al sumar o restar como corresponden los términos semejantes, se obtiene una ecuación de primer grado con una incógnita.
En el segundo sistema, en la primera ecuación está despejada la “x”; conviene usar el “método de sustitución” y aprovechar el despeje para sustituir directamente en la segunda ecuación, efectuar las operaciones correspondientes y encontrar el valor de “y”.
Mientras que, en el tercer sistema, se observan los coeficientes de la incógnita “y” en ambas ecuaciones. Se puede multiplicar alguna de las ecuaciones por “1 negativo” para que se conviertan en simétricas. Por lo tanto, se puede aplicar el “método de reducción”, o despejar “y” en ambas ecuaciones, y utilizar el “método de igualación”.
Lo indispensable al dar solución a un sistema de ecuaciones no es el método empleado, sino la interpretación que se tengan de los valores encontrados para las incógnitas que satisfacen a dicho sistema de ecuaciones.
Sin embargo, se te recomienda que practiques los 4 métodos e identificar cuál es el que más conviene usar con base en el sistema de ecuaciones planteado.
Cuando te enfrentas a un examen, existen algunos reactivos con problemas que implican el uso de sistema de ecuaciones, ¿los has identificado?
¿Qué se piensa sobre la manera por resolver un reactivo de este tipo?, ¿cómo se pueden optimizar tiempos?
A continuación, una sugerencia para dar respuesta a un reactivo con un sistema de ecuaciones en menos de un minuto, dadas las opciones, es la siguiente:
El reactivo dice: ¿Cuál es la solución del sistema de ecuaciones?
Y se presentan 4 opciones de respuesta con los incisos “a”, “b”, “c” y “d”.
Para elegir la respuesta correcta, lo ideal sería dar solución al sistema de ecuaciones por alguno de los métodos conocidos. Pero para optimizar tiempos, la sugerencia es sustituir los valores dados en ambas ecuaciones del sistema, y ver si se cumplen las igualdades. En caso de que alguna de las igualdades no se cumpla, significa que no es la solución del sistema.
Por ejemplo:
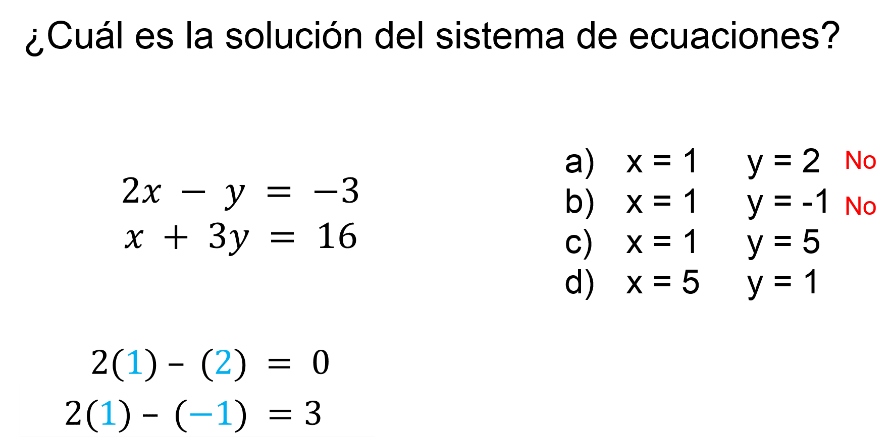
Toma el “inciso a” para sustituir en la primera ecuación el valor de “x” igual a 1, y el valor de “y” igual a 2; se tiene que, 2 por 1 igual a 2, menos 2, igual a cero, y no corresponde a 3 negativo. Como no se cumple la igualdad del sistema, entonces estos valores no son solución del sistema.
Mientras que en el “inciso b”, al sustituir los valores de “x” igual a 1 y “y” igual a 1 negativo, en la primera ecuación se tiene:
2 por 1 es igual a 2, menos 1 negativo es igual a 3 y no tres negativo. De modo que esta opción no hace verdaderas ambas igualdades y tampoco son la solución al sistema.
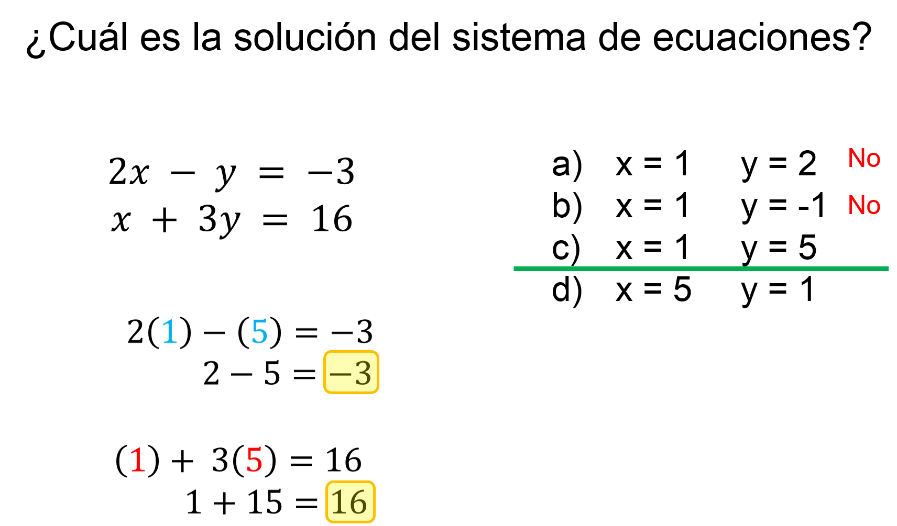
En el caso del “inciso c”, al sustituir en la primera ecuación: 2 por 1 es igual a 2, menos 5 igual a 3 negativo. Como 2 menos 5 es igual a 3 negativo, los valores sí hacen verdadera la igualdad de la primera ecuación.
Sin embargo, para considerarla como la respuesta correcta deberá de cumplir con hacer verdad las dos igualdades.
Se sustituyen los valores en la segunda ecuación: 1 más 3 por 5 igual a 16, y como 1 más 15 valida la igualdad, significa que los valores del “inciso c” son la respuesta correcta del reactivo.
¿Alguna vez te has enfrentado a problemas donde tengas que usar dos ecuaciones lineales con dos incógnitas?
Comprobar que los valores dados en las opciones de respuesta son la solución al sistema de ecuaciones, es una herramienta sencilla de llevar a cabo cuando se resuelven reactivos durante exámenes que tienen un límite de tiempo. Sin embargo, este es un recurso que se emplea únicamente cuando se dominan los métodos de reducción, sustitución, igualación y gráfico para resolver dos ecuaciones lineales con dos incógnitas.
Cristina de Monterrey comparte la siguiente duda:
Mi mamá es cajera de un banco. Una vez ella recibió $500 en monedas de $5 y $10, y la máquina cuenta monedas indicó que eran 82 monedas en total.
Queda la duda: ¿cuántas monedas eran de $5 y cuántas de $10?
Este problema implica la solución de un sistema de ecuaciones lineales con dos incógnitas.
Este problema se reduce a la solución de un sistema de ecuaciones.
Antes de continuar, ya sabes que el propósito específico de la sesión es: aplicar varios procedimientos para resolver problemas.
Consulta en tu libro de texto el aprendizaje esperado: “resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado”, con la finalidad de profundizar en lo aprendido.
El reto de hoy:
Es un ejercicio enviado por Cristina, así es que se retoma para estudiarlo. Ten listo tu cuaderno para anotarlo.
La mamá de Cristina es cajera de un banco; un día recibió $500 en monedas de $5 y $10. La máquina cuenta monedas indicó que eran 82 en total. ¿Cuántas monedas de $5 y cuántas de $10 recibió?

Representa la cantidad de monedas de $5 con una “x” y las monedas de $10 represéntalas con la “y”.
El sistema por resolver es:
“x” más “y” igual a 82
“5x” más “10y” igual a 100
Como una sugerencia: puedes emplear el “método de reducción” o “suma y resta”.
Una vez realizado el reto, realiza la comprobación
Y, finalmente, una síntesis de lo aprendido durante la sesión. En un sistema de dos ecuaciones con dos incógnitas:
- Cada ecuación representa una condición planteada en el problema.
- Las ecuaciones deben de ser lineales, es decir, todas las incógnitas del problema tienen exponente igual a uno.
- Siempre se tiene el mismo número de ecuaciones que de incógnitas.
- En las ecuaciones, las cantidades desconocidas se representan por medio de literales. Generalmente se emplean “x” y “y”, pero puede utilizarse cualquier otra literal.
- La solución es el valor para cada incógnita, los cuales, al ser sustituidos simultáneamente en las dos ecuaciones, se cumplen las igualdades.
- Asimismo, se analizaron las ventajas y desventajas de los 4 métodos revisados.
- Y para concluir, aprendiste la sugerencia para la solución a un reactivo de la guía de estudio para el examen de ingreso a nivel medio superior.
“Sin autodisciplina, el éxito es imposible”.
¡Buen trabajo!
Gracias por tu esfuerzo.
