Resolución de problemas mediante un sistema de ecuaciones lineales 2×2 con el método gráfico
Resolución de problemas mediante un sistema de ecuaciones lineales 2×2 con el método gráfico
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: resolver problemas mediante un sistema de ecuaciones lineales 2×2 con el método gráfico.
¿Qué vamos a aprender?
Conocerás y analizarás la resolución de problemas, con base en el planteamiento y resolución de un sistema de dos ecuaciones lineales, con dos incógnitas o Sistema de Ecuaciones Lineales (2 × 2), mediante el método gráfico; también llamado, método de graficación.
También identificarás que al resolver algunos sistemas de ecuaciones lineales con dos incógnitas puede suceder que:
- Algunos tienen solución única,
- otros tienen un número infinito de soluciones y
- algunos más, no tienen solución.
¿Qué hacemos?
Retomarás un problema propuesto anteriormente, sobre “El equipo de futbol de Néstor”. Ahora, lo resolverás utilizando el mismo Sistema de Ecuaciones Lineales 2 × 2, pero mediante el método gráfico.
Recuerda el problema:
Néstor juega en un equipo de futbol. En esta temporada han tenido un excelente inicio dentro del torneo, pues se mantienen invictos después de jugar los primeros 12 partidos, es decir no han perdido, hasta ahora.
Presta atención en lo que cuenta Néstor:

Como se mencionó anteriormente, en esta lección aprenderás cómo resolver algunos problemas mediante sistemas de ecuaciones lineales 2 × 2, utilizando el método gráfico. Por lo que, es necesario reflexionar en lo siguiente:
¿Qué características tiene este método?
Al ser un método: ¿qué conjunto de pasos se siguen para llevarlo a cabo?

Después de esta precisión, conoce los pasos a seguir en el método gráfico:
- Plantear el Sistema de Ecuaciones Lineales 2 × 2, con base en los datos identificados en el enunciado del problema propuesto.
- Despejar la incógnita “y” en ambas ecuaciones.
- Asignar valores a la literal “x” y sustituirlos, en los correspondientes despejes de “y”, para obtener los valores de “y”, formándose pares ordenados (x, y). Asimismo, elaborar una tabla para organizar los datos de cada ecuación.
- Elaborar, en un mismo plano cartesiano, la gráfica de cada una de las ecuaciones que forman el sistema.
- Interpretar la gráfica resultante, para identificar la solución del sistema y con ello, la solución del problema.
Paso 1. Plantear el Sistema de Ecuaciones Lineales 2 × 2
El equipo de Néstor tiene doce juegos jugados, de los cuales han ganado algunos y empatado otros.
¿Qué ecuación permite representar cuántos juegos ganaron y cuántos juegos empataron?

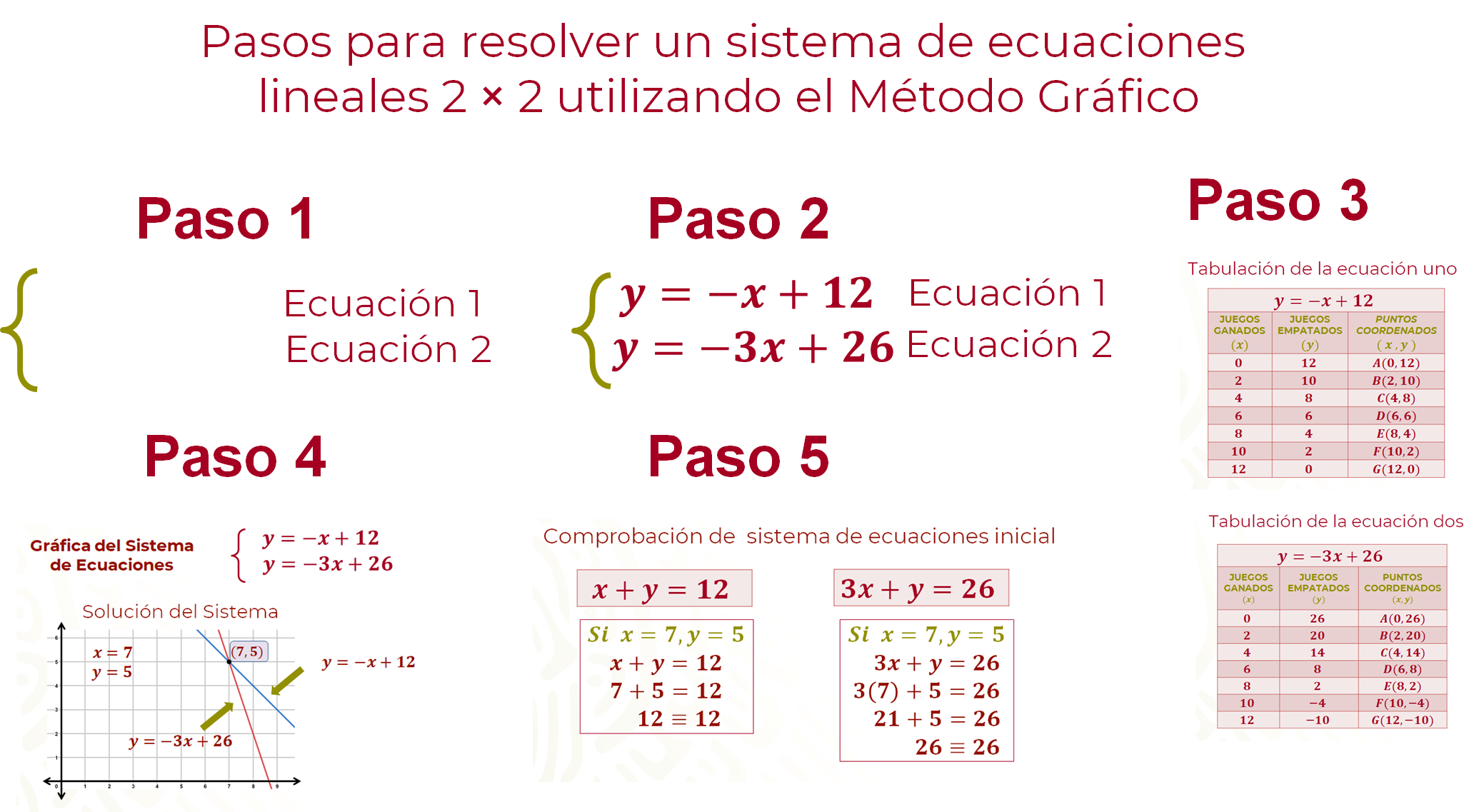
Ahora, analiza que al sumar el número de los juegos ganados más el número de los juegos empatados, obtienes el número de los juegos jugados durante el torneo; donde “equis” representa los partidos ganados y “y” representa los partidos empatados, y el doce es el número de los juegos efectuados durante el torneo de manera invicta.
Por lo tanto, la primera ecuación queda definida como “x” mas “y” igual a doce.
Recuerda que el equipo de Néstor sumo veintiséis puntos, por cada juego ganado obtendrá tres puntos y si empata un punto.
¿Qué ecuación permite representar, cuántos juegos ganó y cuántos juegos empató?
La ecuación queda representada como tres por “equis” más “ye” igual a veintiséis.

¿Por qué?
Porque, los juegos ganados valen tres puntos, por lo tanto, se multiplica tres por “equis” más los juegos empatados igual al total de puntos del torneo.
¿Por qué es un sistema de ecuaciones?
Se considera un sistema, porque hay una relación entre las ecuaciones, es decir los puntos obtenidos por el equipo de Néstor están relacionados con el número de juegos ganados y empatados.
Por lo tanto, el sistema de ecuaciones lineales con dos incógnitas (2×2) que permite resolver el problema de Néstor, es:
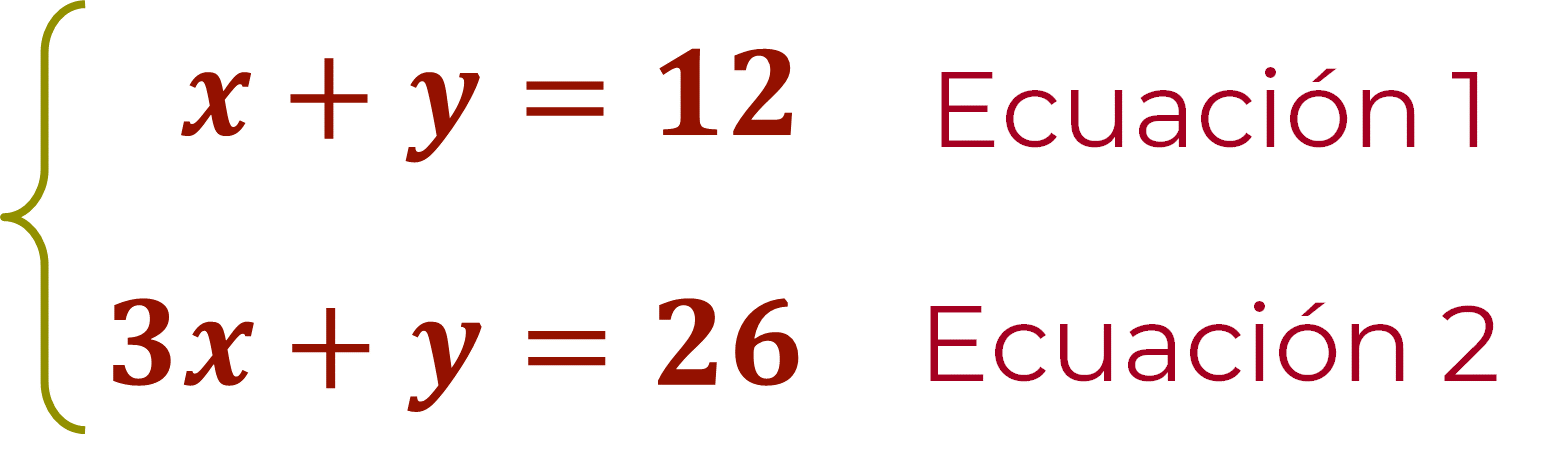
Paso 2. Despejar la incógnita “y” en ambas ecuaciones.
Para encontrar soluciones de una ecuación lineal con dos incógnitas del tipo de ecuaciones que forman el sistema, es común que primero se exprese cada ecuación en términos de “y”, es decir se despeja “ye”.

Ordenando los términos de la expresión del lado derecho queda:
y = -x + 12
¿Qué representa la ecuación uno en la situación de Néstor?
Permite representar cómo calcular los juegos empatados a partir de la diferencia de los juegos ganados con el número total de los juegos realizados.
Continua con el despeje de la incógnita “y” en la ecuación dos.

Ordenando los términos de la expresión del lado derecho queda:
y = -3x + 26
¿Qué representa la ecuación dos en la situación de Néstor?
Permite representar cómo calcular los juegos empatados en relación con la diferencia de los puntos obtenidos por cada victoria y los puntos obtenidos hasta el momento en el torneo.
Por lo tanto, el sistema de ecuaciones con despejes de “y”, queda de la siguiente forma:
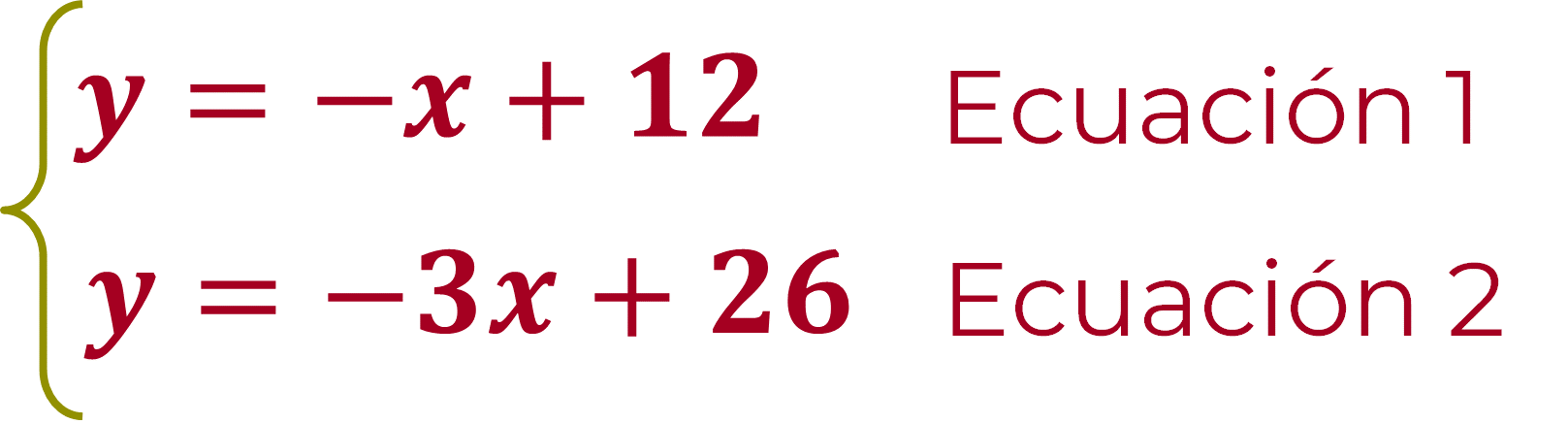
Paso 3. Asignar valores a la literal “x” y sustituirlos en los correspondientes despejes de “y”.
Al mismo tiempo, comenzarás a elaborar una tabla para organizar los datos de cada ecuación considerando tres columnas: una columna para registrar los valores asignados a “x”, una segunda columna para registrar los valores de “y” y una tercera columna para registrar los puntos coordenados (x, y)
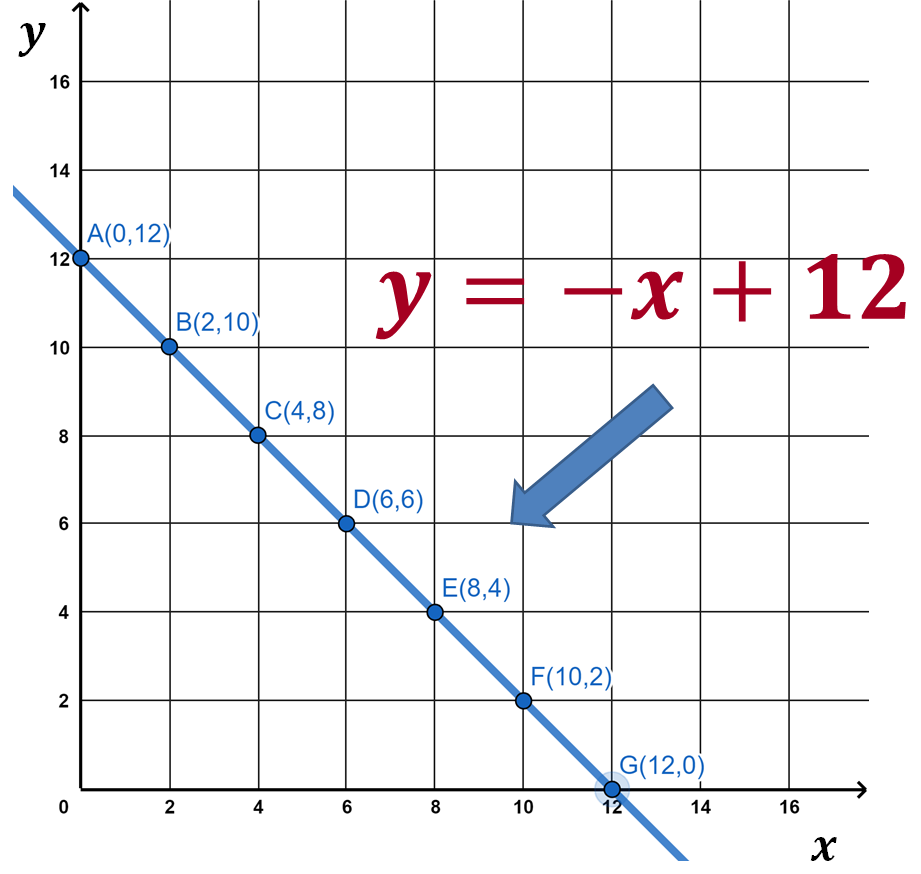
Procede a realizar la tabulación de la ecuación uno, utilizando el despeje de “y”.
Partirás da la expresión:
y = -x + 12
Ahora, asigna los siguientes valores a “equis”: 0, 2, 4, 6, 8, 10 y 12. Estos valores asignados a “x”, son los partidos ganados.
Sustituye cada valor de “x” en la ecuación para obtener los valores correspondientes de “y”.

Por lo tanto:
Si “x” toma el valor de cero, “y” es igual a doce
Si “x” toma el valor de dos, “y” es igual a diez.
Si “x” toma el valor de cuatro, “y” es igual a ocho.
Si “x” toma el valor de seis, “y” es igual a seis.
Si “x” toma el valor de ocho, “y” es igual a cuatro.
Si “x” toma el valor de diez, “y” es igual a dos.
Si “x” toma el valor de doce, “y” es igual cero.
¿Qué significan los valores de “x”?
Representan los juegos ganados.
¿Qué significan los valores de “y”?
Representan los juegos empatados.
Ahora comienza a elaborar una tabla para organizar los datos obtenidos después de realizar la sustitución de los valores asignados a “x” en la ecuación uno, en particular en el despeje de “y”.
Tu tabla tendrá tres columnas: una columna para registrar los valores asignados a “x”, una segunda columna para registrar los valores de “y” y una tercera columna para registrar los puntos coordenados (x, y).
Tabulación de la ecuación 1

¿Cómo formas los puntos coordenados?
Cada punto lo nombraras utilizando letras mayúsculas y colocando dentro de un paréntesis los valores de “x” y de “y”, recordarás que siempre el primer valor será el de las abscisas o de las “x” y el segundo valor será el de las ordenadas o de las “y”.
Gráfica del Sistema de Ecuaciones
(ecuación 1)
Procede a realizar la tabulación de la ecuación dos, utilizando el despeje de “y”.
Partirás de la expresión:
y = -3x + 26
Asigna los siguientes valores a “equis”: 0, 2, 4, 6, 8, 10 y 12.
¿Qué significan estos valores asignados a “equis”?
Los partidos ganados.
Ahora sustituye cada valor de “x” en la ecuación “y” para obtener los valores correspondientes.
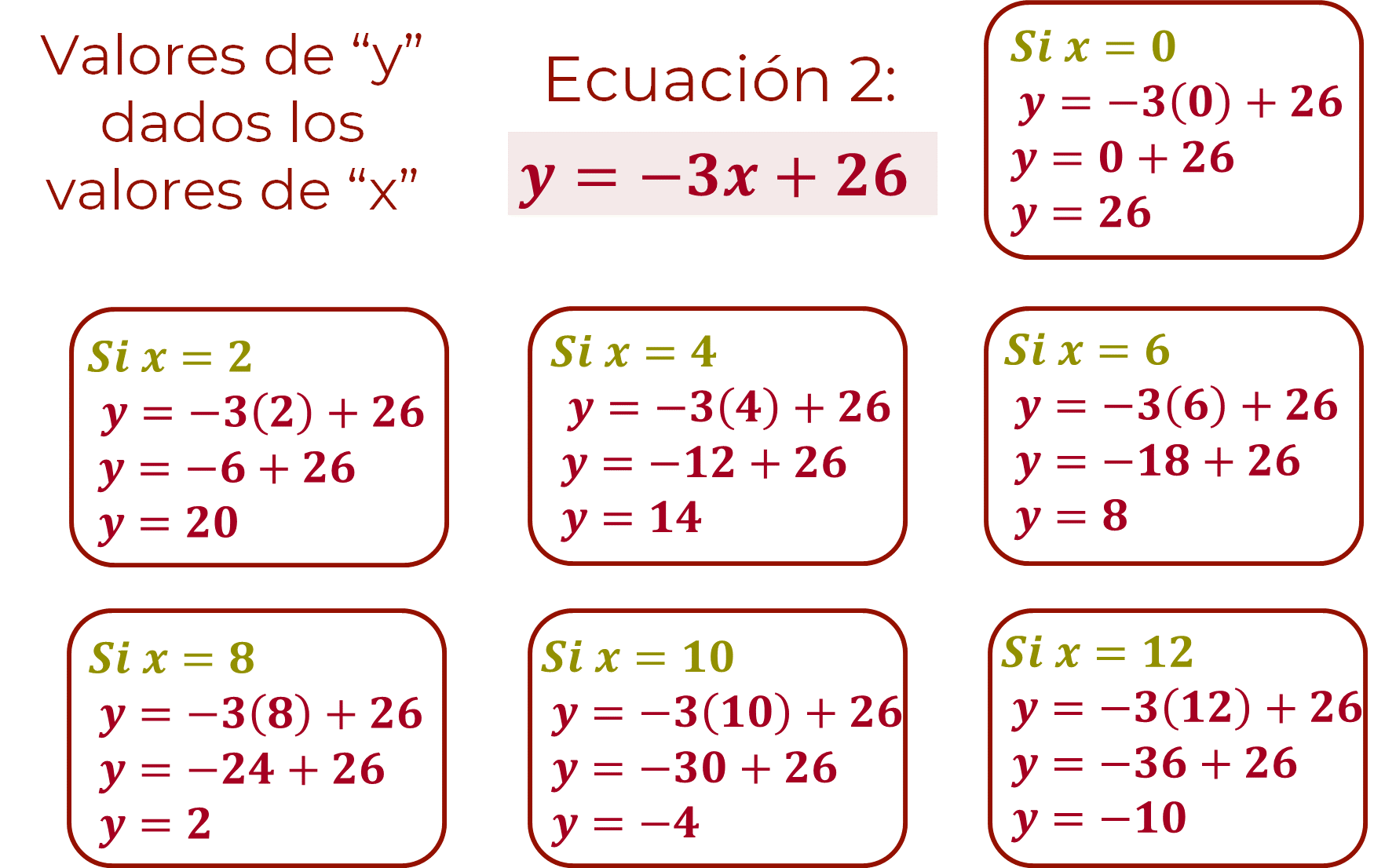
Por lo tanto:
Si “x” toma el valor de cero, “y” es igual a veintiséis.
Si “x” toma el valor de dos, “y” es igual a veinte.
Si “x” toma el valor de cuatro, “y” es igual a catorce.
Si “x” toma el valor de seis, “y” es igual a ocho.
Si “x” toma el valor de ocho, “y” es igual a dos.
Si “x” toma el valor de diez, “y” es igual a cuatro negativo.
Si “x” toma el valor de doce, “y” es igual a diez negativo.
En la siguiente tabla se presenta la organización de los datos obtenidos después de realizar la sustitución de los valores asignados a “x” en la ecuación dos, en particular en el despeje de “y”.
De la misma manera la tabla tendrá tres columnas: una columna para registrar los valores asignados a “x”, una segunda columna para registrar los valores obtenidos de “y” y una tercera columna para registrar los puntos coordenados (x, y).
Tabulación de la ecuación 2

¿Cómo formas los puntos coordenados?
Cada punto lo nombrarás utilizando letras mayúsculas colocando dentro de un paréntesis los valores de “x” y de “y”, recuerda que siempre el primer valor será el de las abscisas o de las “x” y el segundo valor será el de las ordenadas o de las “y”.
Gráfica del Sistema de Ecuaciones
(ecuación 1)
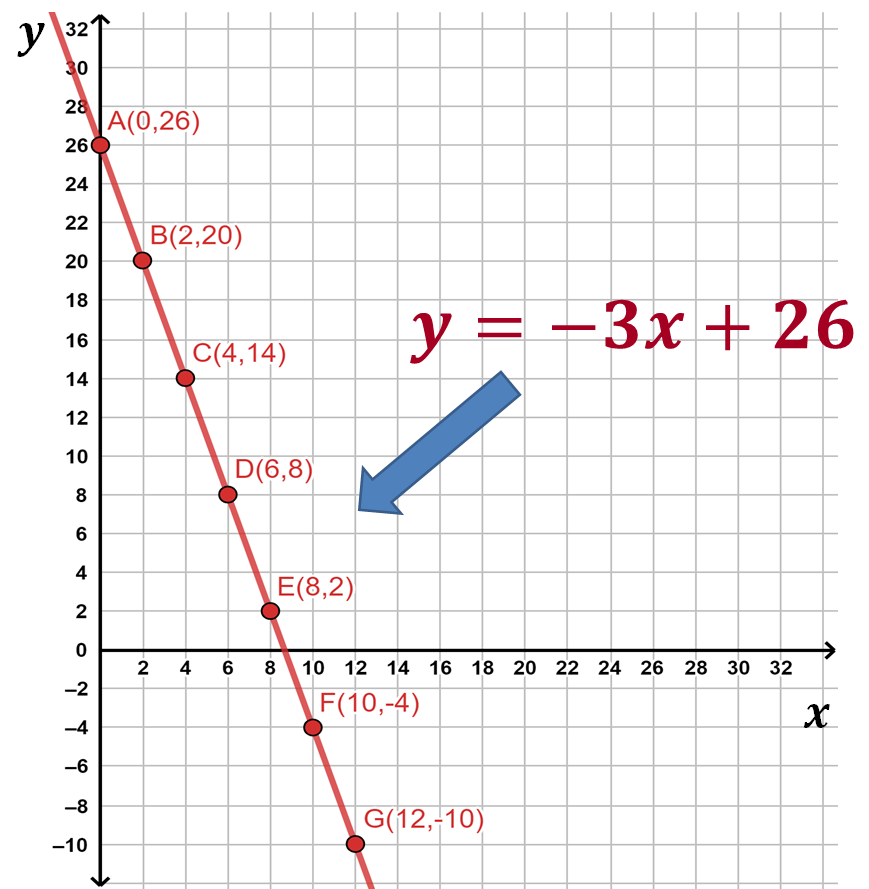
Ahora, ubica los puntos coordenados (“x”, “y”), que obtuviste en las tablas elaboradas de cada ecuación en el plano cartesiano. Es necesario ubicar cada punto coordenado, después trazar una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula.
Paso 4. Elabora en un mismo plano cartesiano la gráfica de la ecuación uno y ecuación dos que forman parte del sistema.
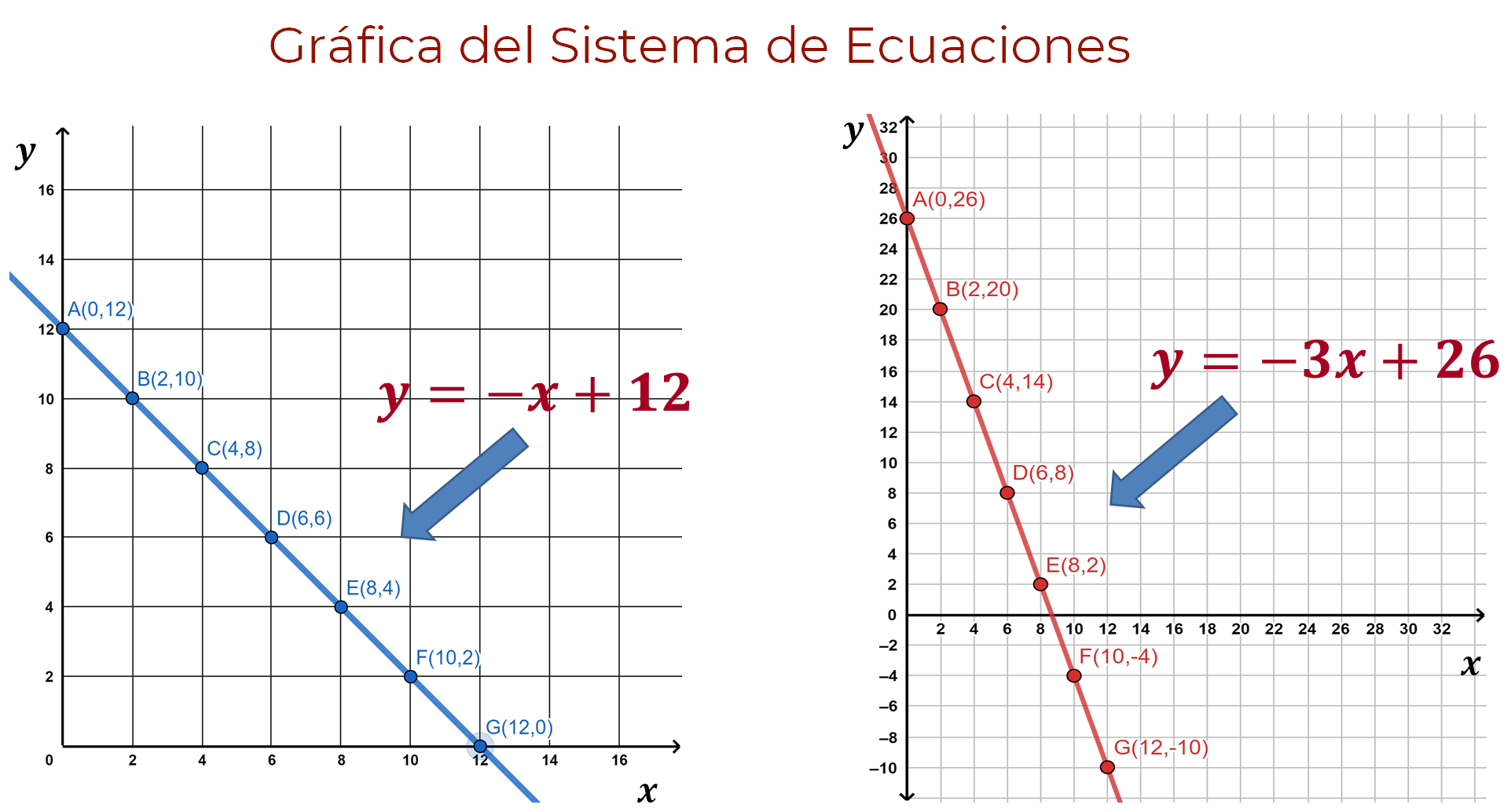
Se obtiene una línea recta que representa el comportamiento de la ecuación, es decir, la relación que se da entre los partidos ganados y empatados, así como los puntos obtenidos por el equipo de Néstor.
Observa que las rectas en la gráfica representan una pendiente negativa, de más “y” a menos “y” y de menos “x” a más “x”, es decir, si aumentan los juegos ganados disminuirán los juegos empatados.
Es importante escribir la expresión algebraica de la ecuación uno y ecuación dos en su versión del despeje de “y”, señalando a qué recta corresponde mediante una flecha.
Paso 5. Relacionar e interpretar las gráficas resultantes para identificar la solución del sistema y con ello la solución del problema.
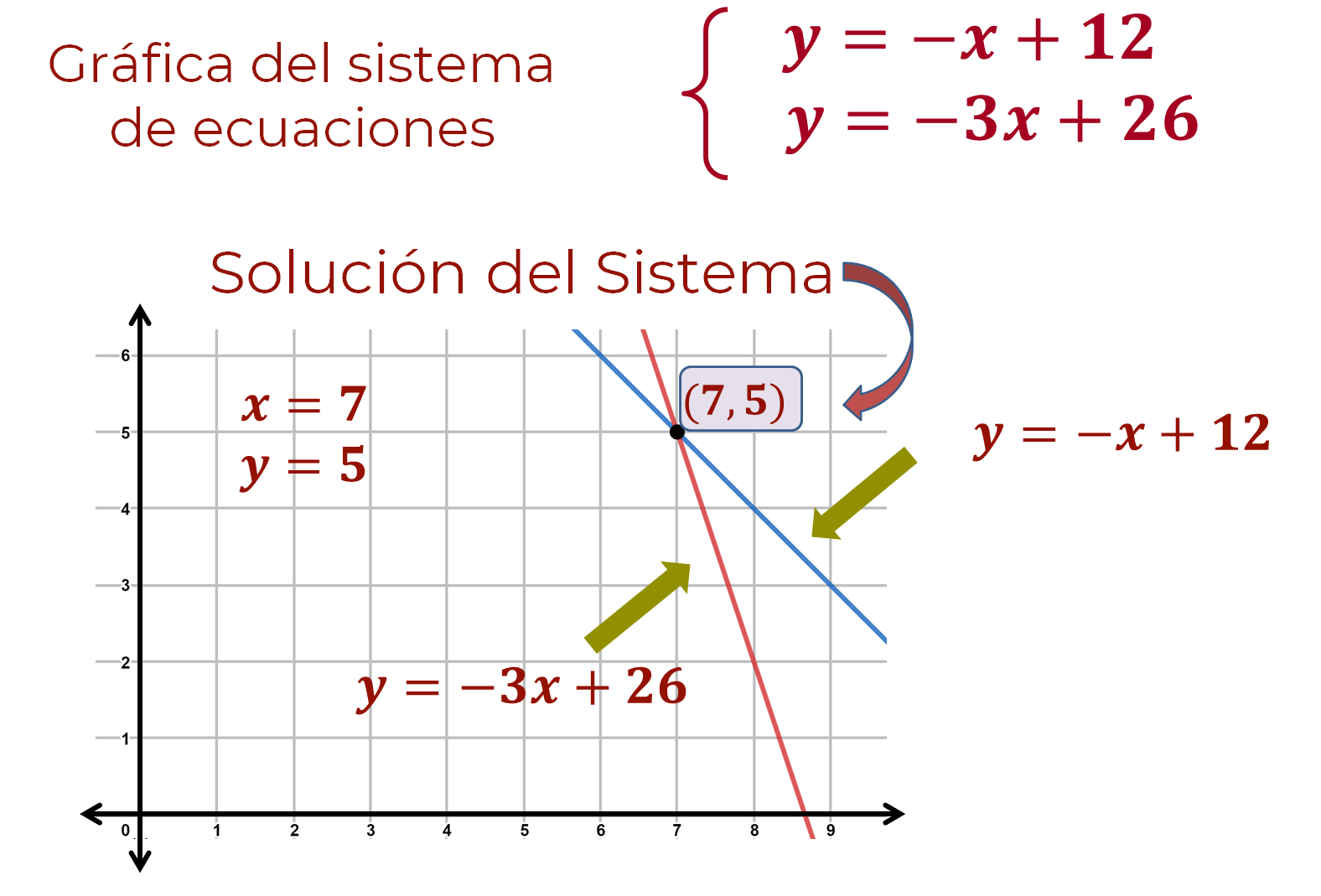
Observa que hay un punto donde se unen las líneas rectas de las ecuaciones en el plano cartesiano, estas se unieron en el punto P (7,5), como se muestra en la gráfica.
¿Cómo se le llama a este punto?
Punto de intersección o solución del sistema.
¿Cuáles son las coordenadas del punto de intersección?
Un primer valor de “x” y un segundo valor de “y”, esto es: 7, 5.
¿Qué representan las coordenadas del punto de intersección de las dos líneas rectas en el contexto del problema?
Las coordenadas del punto de intersección, es decir la abscisa “x” representa los partidos ganados y la ordenada “y” representa los partidos empatados.
Ahora comprueba que los valores obtenidos para “x” y para “y” son correctos en el sistema de ecuaciones lineales 2×2 planteado, para definir la solución del problema.
Observa las ecuaciones uno y dos planteadas al principio del problema.
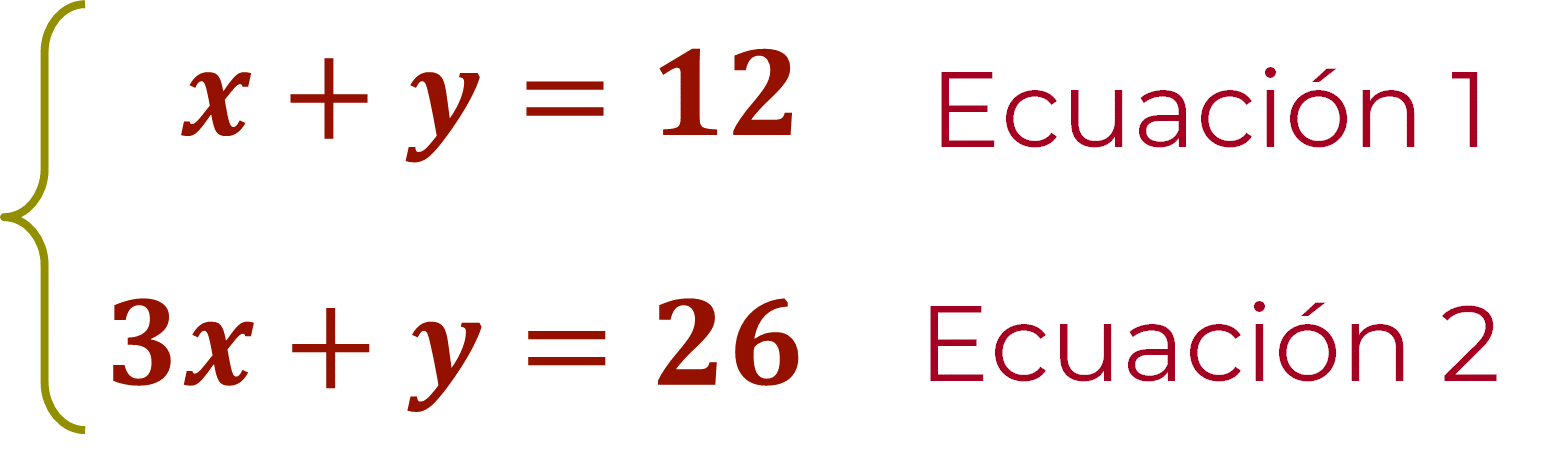
¿Qué representa la ecuación uno donde “x” más “y” es igual a doce?
“x” representa los partidos ganados, y “y” representa los partidos empatados, esto es igual a los doce partidos jugados.
Sustituye los valores de las coordenadas del punto de intersección, en la ecuación uno, donde, “x” es igual a siete y “y” es igual a cinco, al operar siete más cinco es igual a doce, por lo tanto, se obtiene una identidad y se puede afirmar que dichos valores hacen verdadera la igualdad.
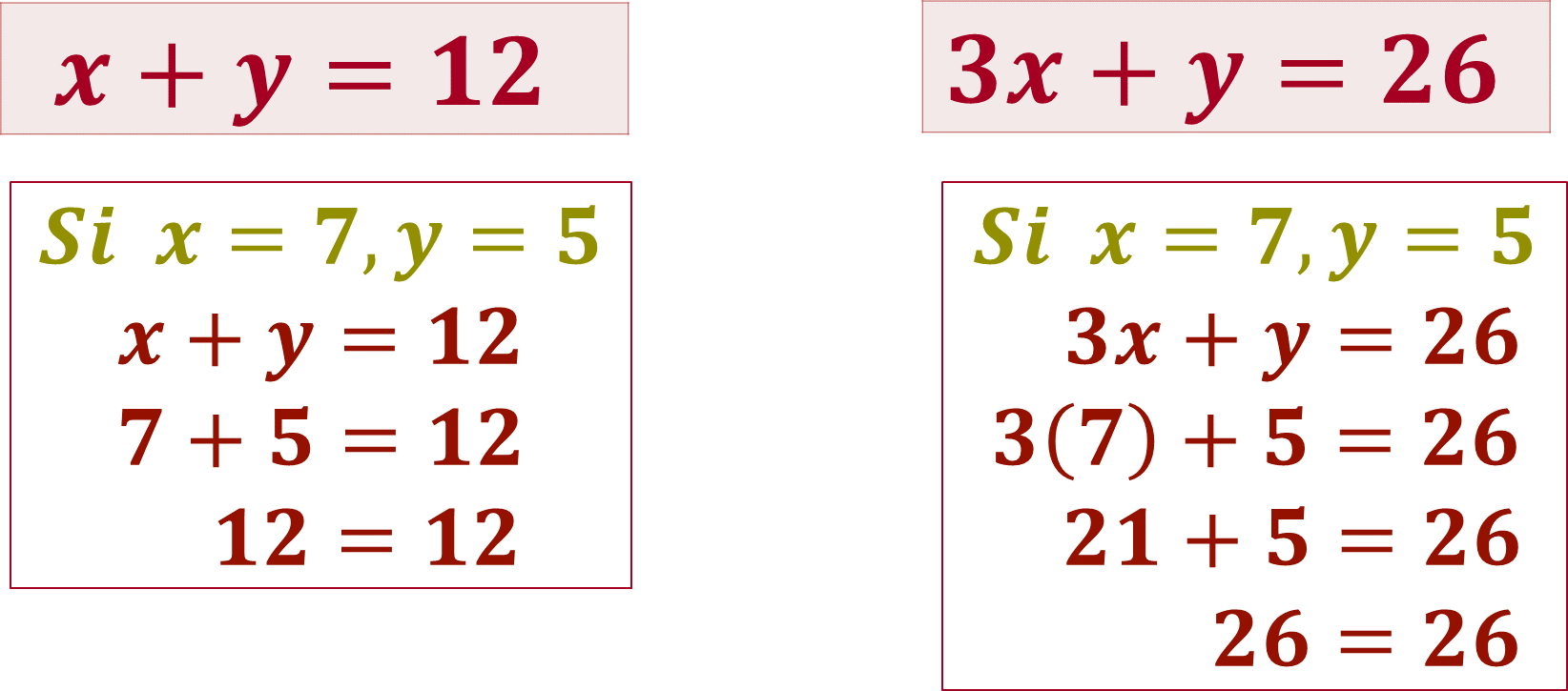
¿Qué significa esta igualdad?
La solución del problema, es decir, que el equipo de Néstor ganó siete partidos y empató cinco.
¿Qué representa la ecuación “3x” más “y” igual a veintiséis?
Tres son los puntos que dan por partido ganado, “x” los partidos ganados más “y” los partidos empatados que equivalen a un punto, igual a los veintiséis puntos ganados por el equipo de Néstor.
Sustituye los valores de las coordenadas del punto de intersección, en la ecuación dos, donde “x” es igual a siete y “y” es igual a cinco, al operar tres por siete más cinco es igual a veintiséis, por lo tanto, se da la identidad en la ecuación dos.
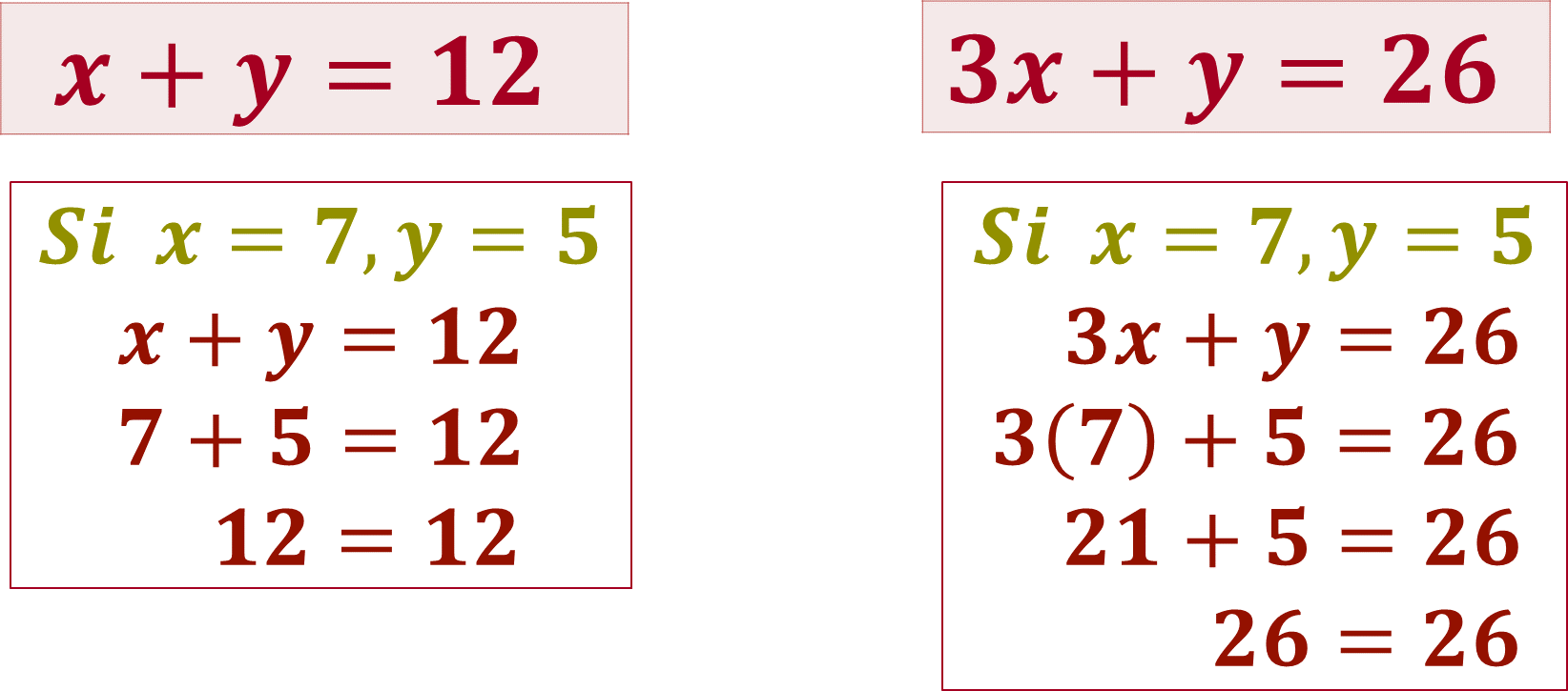
¿Qué significa esta identidad?
La solución del problema, es decir que el equipo de Néstor obtuvo veintiún puntos mediante siete partidos ganados y cinco puntos mediante cinco empates.
Ahora, responde a Néstor su pregunta inicial:
¿Sabes cuántos partidos ganamos y cuantos empatamos?
El equipo de Néstor ganó siete y empató cinco partidos de futbol sumando un total de veintiséis puntos.
Sigue respondiendo a Néstor:
¿Qué sistema de ecuaciones lineales 2×2 se planteó permitiendo resolver el problema?
X + y = 12
3x + y = 26
En conclusión: Es un sistema de ecuaciones con una única solución.
A continuación, reflexiona en lo siguiente:
¿Qué tipo de situaciones pueden presentarse cuando se resuelve un sistema de ecuaciones lineales 2×2 utilizando el método gráfico?
Cuando se grafica un sistema de dos ecuaciones lineales con dos incógnitas puede ocurrir una de las siguientes situaciones con el sistema propuesto:
- Que tenga una única solución.
- Que tenga infinidad de soluciones.
- Que carezca de solución.
Observa la siguiente imagen al respecto:
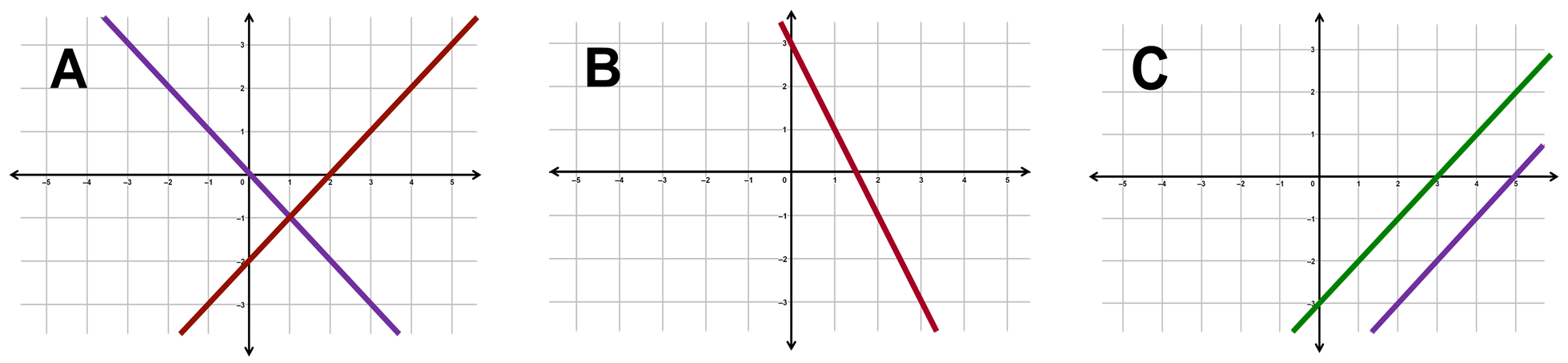
En la gráfica A, puedes observar que se unen las líneas rectas obtenidas de las ecuaciones lineales con dos incógnitas de un sistema, por lo tanto, se puede afirmar que el sistema tiene una única solución.
En la gráfica B, puedes observar que no hay unión entre las dos líneas rectas obtenidas de las ecuaciones lineales con dos incógnitas de un sistema, dichas líneas están, una encima de la otra, por lo tanto, se puede afirmar que el sistema tiene una infinidad de soluciones.
En la gráfica C, puedes observar que no hay unión entre las dos líneas rectas obtenidas de las ecuaciones lineales con dos incógnitas de un sistema, dichas líneas son paralelas entre sí, por lo tanto, se afirma que el sistema no tiene solución.
En esta clase identificaste el proceso de resolución de un sistema de ecuaciones lineales (2×2) mediante el método grafico
El cual consiste en:
- Plantear el Sistema de Ecuaciones Lineales 2×2
- Despejar la incógnita “y” en ambas ecuaciones
- Asignar valores a la literal “x” y sustituirlos en los correspondientes despejes de “y”.
- Elaborar en un mismo plano cartesiano la gráfica de cada ecuación que forman el sistema.
- Interpretar la gráfica resultante para identificar la solución del sistema y con ello la solución del problema.
El reto de hoy:
Resuelve algunos de los problemas o ejercicios sobre Sistemas de Ecuaciones Lineales 2×2 con el Método Gráfico que identifiques en tu libro de matemáticas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/