Resolución de problemas integradores. Sentido numérico y pensamiento algebraico I
Resolución de problemas integradores. Sentido numérico y pensamiento algebraico I
Aprendizaje esperado: desarrolla habilidades que le permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Énfasis: consolidar la resolución de problemas. Sentido numérico y pensamiento algebraico I.
¿Qué vamos a aprender?
Te apoyarás en una serie de reactivos del tipo de los que suelen aparecer en pruebas de selección para el ingreso a una escuela o nivel de educación medio superior, por ejemplo, la Comipems.
Trabajarás sobre los conocimientos acumulados y los medios o técnicas que ayuden a incrementar la posibilidad de éxito al participar en estas evaluaciones.
Para el desarrollo de los contenidos correspondientes necesitarás tu cuaderno de notas, un bolígrafo, un lápiz y goma.
Procura registrar tus dudas, inquietudes y anotaciones respecto a los contenidos que se presentarán.
¿Qué hacemos?
La evaluación resulta una actividad esencial e imprescindible en la mayoría de los ámbitos de acción de la humanidad, desde saber si un fruto está maduro para cosecharlo, hasta comprobar la resistencia del fuselaje de un avión.
Comparar las características de un elemento con otras preexistentes que determinan correspondencia es una práctica común.
En el ámbito escolar, se ha asociado a la evaluación con la presentación de exámenes y pruebas que determinan una calificación numérica.
Durante cada etapa del trayecto formativo, se desarrollan habilidades y aprendizajes que se manifiestan paulatinamente en las conductas y la solución de problemas, tanto escolares como de la vida cotidiana.
Sin embargo, en el ámbito escolar es necesario contar con indicadores confiables de la eficiencia de la actividad escolar.
Las pruebas escritas representan un útil recurso que proporciona información al respecto, sin ser la única opción, pero es la que estudiarás.
Observa el siguiente video del inicio al segundo 00:38.
- Información de los nuevos instrumentos de evaluación
La prueba escrita, particularmente la de opción múltiple, es un instrumento de evaluación que representa un eficiente medio en la valoración de aprendizajes y conocimientos.
Es por ello que se aplican este tipo de pruebas de opción múltiple en la selección de personal en las empresas. También sirven como indicadores de resultados de programas institucionales y, por supuesto, como prueba de conocimiento para acceder a determinadas escuelas o niveles educativos.
Como estudiante, te encuentras con frecuencia frente a este tipo de pruebas. Por esta razón conocerás una serie de reactivos que permitan proponer soluciones y sugerencias sobre cómo enfrentar las pruebas escritas de opción múltiple.
Naturalmente las correspondientes a Matemáticas y en particular las relacionadas al eje “Sentido numérico y pensamiento algebraico”.

La mayoría de las pruebas escritas de opción múltiple contienen una cantidad considerable de reactivos por lo que el tiempo para resolverlos se vuelve un importante factor a considerar.
Se tiene que la respuesta correcta es la opción “C”.
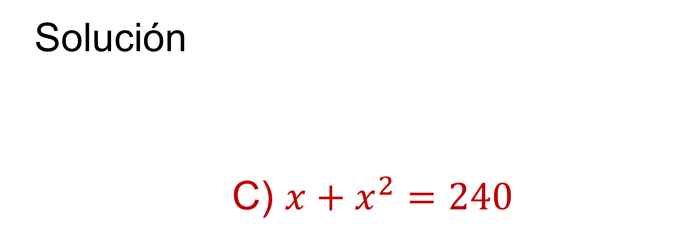
Al justificar la respuesta se hace mención en el enunciado “un número desconocido”, que se puede representar con una letra, “x” en este caso. Un término algebraico es cuadrático o de segundo grado o está la segunda potencia, si su exponente es 2.
Como puedes observar, debes apelar al repertorio completo de conocimientos y habilidades matemáticas de que dispones. Pero también son útiles otras habilidades comunes, como se pondrá en evidencia durante estas soluciones.

Solución correcta, más menos seis.
El objetivo es contestar correctamente cada reactivo empleando el menor tiempo posible. Los conocimientos y habilidades previas son lo que muchas veces determinan ese tiempo. Observa la justificación.
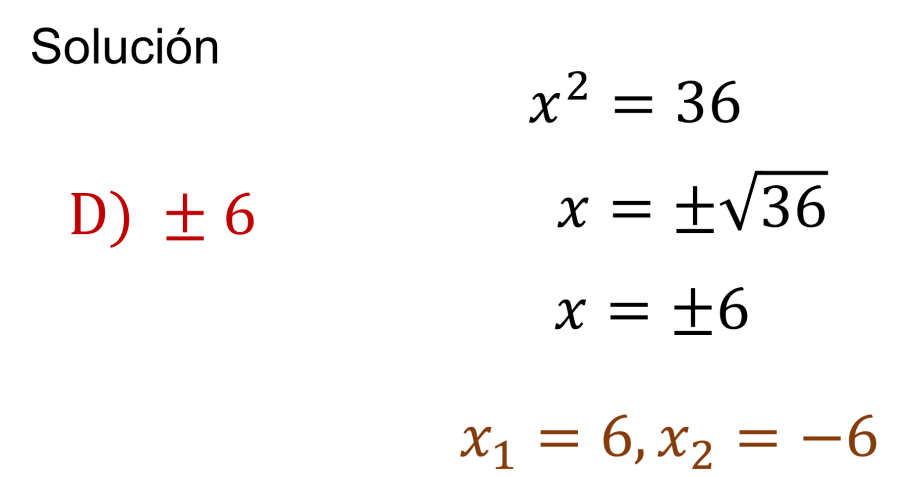
Al observar la expresión que representa la ecuación, el exponente mayor de la incógnita es 2, por lo que es una ecuación de segundo grado. Y las ecuaciones de segundo grado tienen dos soluciones o raíces, en este caso son 6 y 6 negativo.
También se identifica que es una ecuación de la forma “a” “x” al cuadrado más “C” igual a cero”, que se puede resolver por despeje. Y al completar el despeje correspondiente, “x” es igual a más menos raíz cuadrada de 36. Hay dos números cuyo cuadrado es 36. Estos son 6 y 6 negativo.
Al resolver este tipo de pruebas, no siempre es necesario escribir cada detalle del procedimiento que da solución a cada problema. Más bien se trata de movilizar conocimientos y habilidades, tanto formales como empíricos para ser eficientes al seleccionar la opción correcta.
Saber el número de soluciones según el grado de una ecuación, así como del concepto y propiedades de la raíz cuadrada, son aspectos que ayudarán a resolver con presteza preguntas de ese tipo.

Al saber que es una ecuación, se supondría que la única manera de conocer la solución correcta es desarrollando toda la resolución de la ecuación.
Sin embargo, hallar las raíces de la ecuación significa saber para cuáles valores la expresión se hace válida. Y puesto que ya se conoce una de las raíces, se puede evaluar si al sustituir alguna de las opciones, la igualdad se cumple.
Utiliza para ello el uso de la multiplicación de números y las potencias.

La expresión que representa la ecuación indica que un número, representado por “x”, se eleva al cuadrado y se suma al producto de tres por ese mismo número.
De las opciones que ofrece el reactivo, la opción “A”, negativo tres, cumple con esa condición.
Al sustituirlo en la ecuación y realizar las operaciones indicadas se observa que la igualdad se cumple.
Se tiene tres negativo al cuadrado más tres por negativo tres debe ser cero.
Negativo tres al cuadrado es nueve y tres por negativo tres es nueve negativo, así nueve más nueve negativo es cero.
Cero igual a cero tiene sentido. Por lo tanto, es la opción correcta.
Contar con ese tipo de recursos abreviará el tiempo de respuesta. Pero si no lo puede abordar de esa manera, es preferible resolver la ecuación. Resultará más laborioso evaluar dos o tres o todas las opciones que resolver de manera ordenada la ecuación.
La manera más práctica de resolver esta ecuación de la forma “a” “x” al cuadrado más “b” “x” igual a cero es mediante la factorización.

Ya que la ecuación está en la forma general se factoriza el primer miembro de la igualdad.
En este caso, el factor común, es “x”.
La expresión indica, literalmente, que al multiplicar “x” por “x” más tres es igual a cero.
La única manera de que al multiplicar dos términos el resultado sea cero, es que alguno de ellos o ambos factores sea cero.
Por eso, cada factor se iguala con cero, lo que da lugar a dos ecuaciones de primer grado que se pueden resolver por despeje.
La primera de estas nuevas ecuaciones ya está despejada. Equis uno vale cero. Tal como lo indicaba el enunciado de este reactivo.
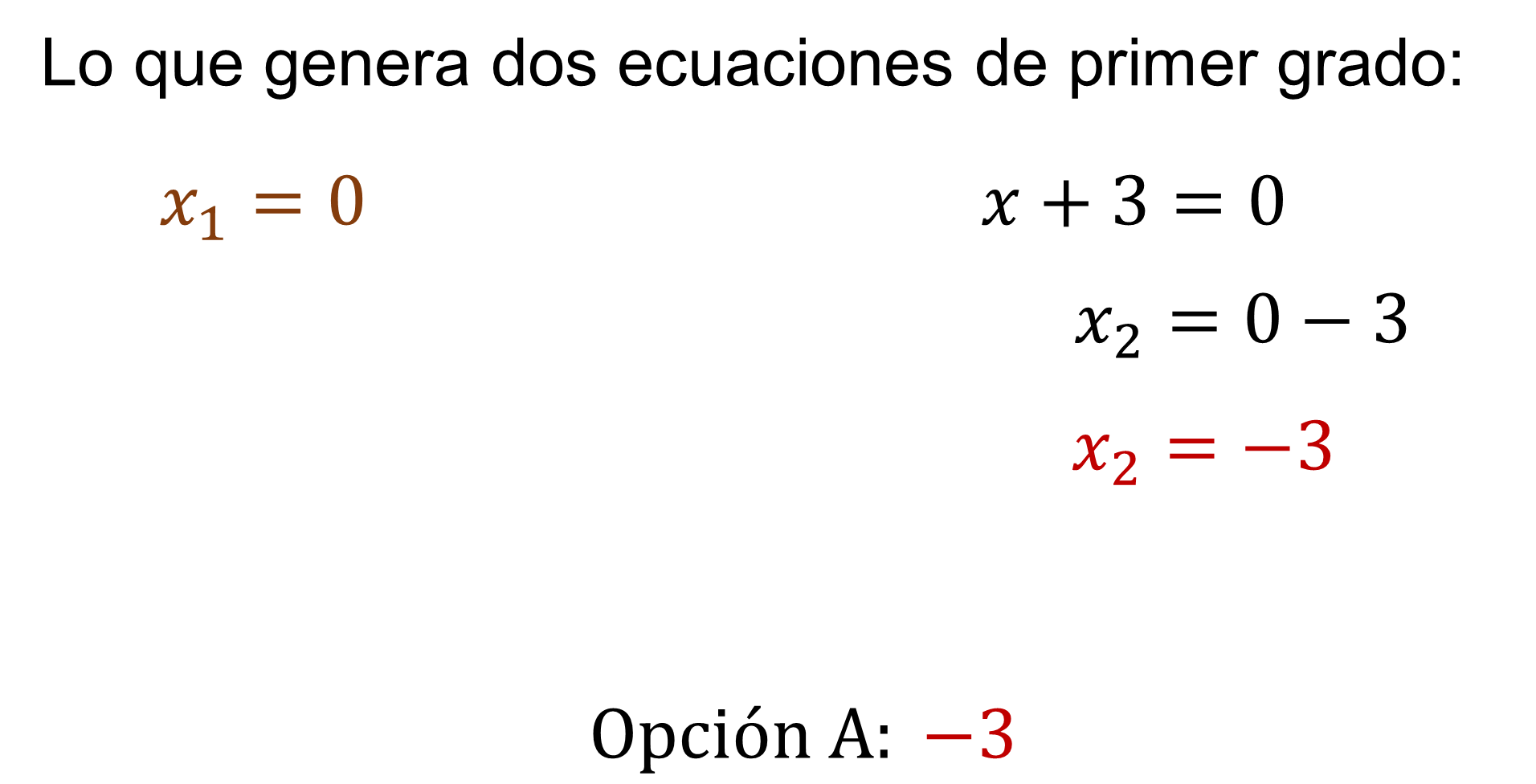
Y al despejar la segunda ecuación se obtiene la otra raíz. “X” dos es igual a tres negativo.
Correspondiente a la opción “A”.
Como has podido notar, la brevedad o simpleza de la solución a cada reactivo estriba en los recursos con que se cuenta para enfrentar este tipo de pruebas.
Si no cuentas con las habilidades que se han presentado, aún hay otro recurso.
Es un poco más laborioso, pero también lleva a la respuesta correcta. Se trata de la fórmula general.
La fórmula general sirve para resolver cualquier ecuación cuadrática o de segundo grado.
Cuya solución arrojará también los mismos valores para las raíces de la ecuación, cero y tres negativo, confirmando que la opción correcta es la “A”.
Cabe destacar que la mayoría de las veces existe más de una manera de resolver un problema matemático. La practicidad de la solución depende, como se ha expuesto, de los conocimientos, habilidades y experiencia que poseas.
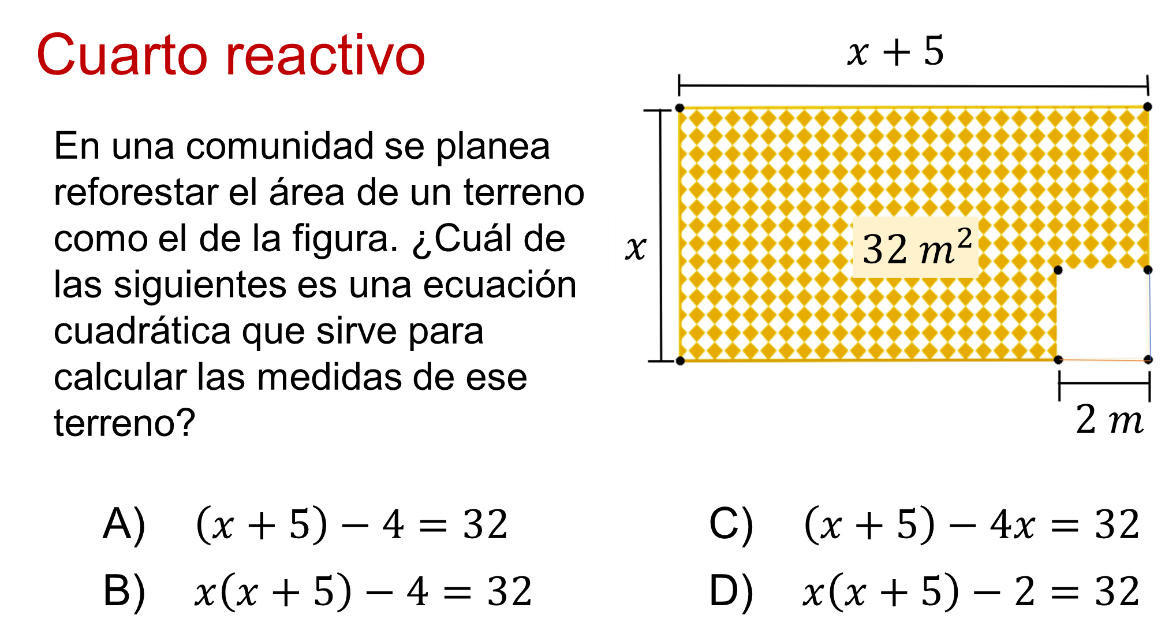
Considera que mucho del éxito al resolver cada reactivo consiste en leer y entender con claridad lo que se solicita. También analiza las figuras o esquemas que acompañan al enunciado para encontrar información adicional, de ser el caso.
Al leer el enunciado, se pregunta cuál de las opciones es una ecuación cuadrática.
Primero debes considerar que no se pide calcular los lados, pide elegir una expresión.
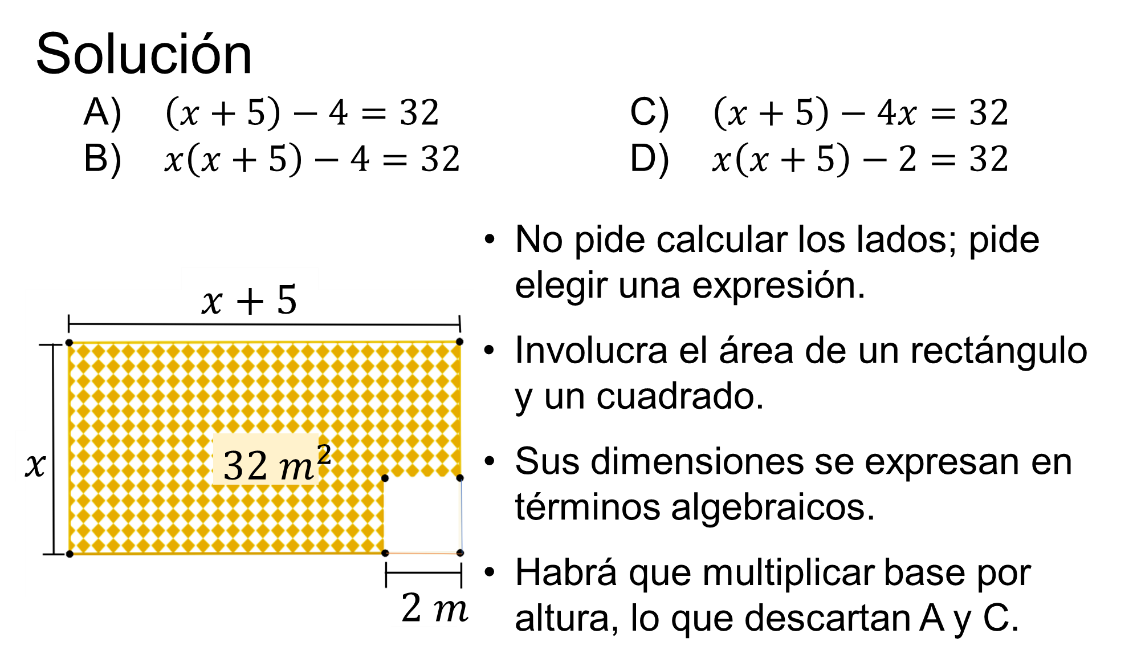
Luego, involucra el área de un rectángulo y un cuadrado y sus dimensiones se expresan en términos algebraicos.
Habrá que multiplicar base por altura, lo que descartan “A” y “C”, pues muestran expresiones lineales o de primer grado.
Se sabe porque el exponente mayor de la incógnita en ambos casos es uno.
La manera más simple de dar respuesta es representar las áreas de forma algebraica.
Al área del rectángulo se le resta el área del cuadrado.
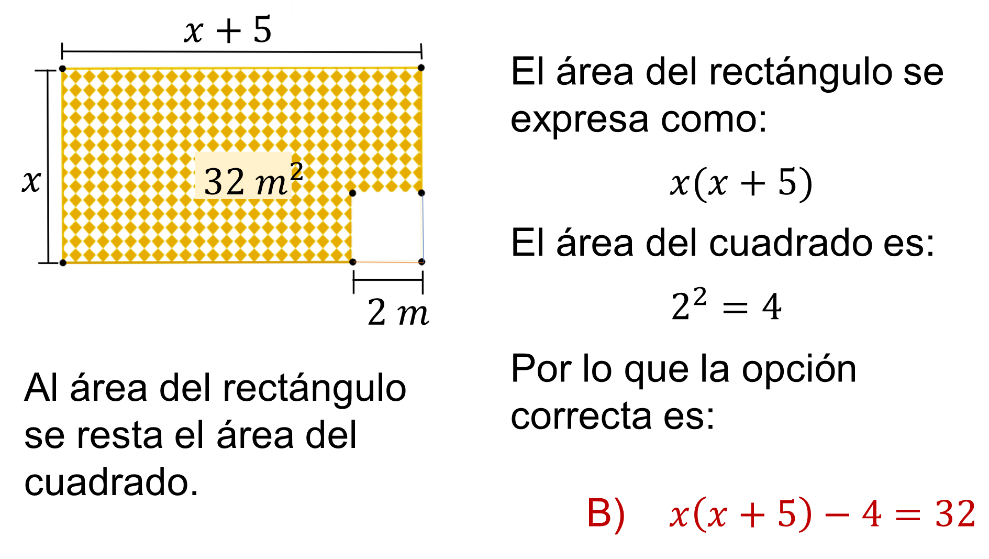
Para el rectángulo se multiplica el largo por el ancho y se tiene “x” por “x” más 5.
Mientras que para el cuadrado es 2 al cuadrado igual a 4.
Al restarlos se obtiene la expresión “x” por “x” más 5, menos 4 igual a 32, representada en la opción “B”.
Al resolver reactivos, como el que se acaba de mostrar, se debe ser práctico. Es común que al encontrar un problema que parece accesible de acuerdo a la experiencia se quiera dar solución a la ecuación completa, demostrar lo que se sabe y hallar las dimensiones de la figura. Sin embargo, debes entender y discriminar sólo lo necesario.
Las expresiones que se ofrecieron como opciones ni siquiera están simplificadas y ordenadas en la forma general. Así que debes abordar cada situación con la profundidad que requiere. Sin complicarse de más.

No pierdas de vista que este tipo de exámenes te pone a prueba, así que las soluciones no tienen que ser necesariamente inmediatas, pero sí alcanzables según los conocimientos que poseen.
Se destaca las condiciones del enunciado, dos números cuyo producto o multiplicación es 84 negativo, y cuya suma es igual a 5.
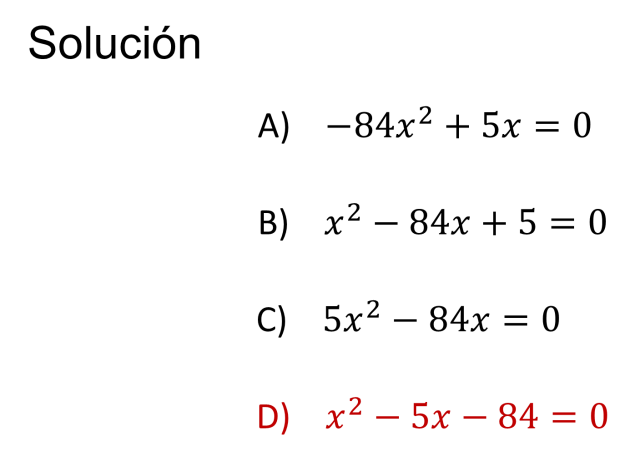
Ya conoces cómo se encuentran los términos “no comunes” al factorizar un trinomio de segundo grado.
Todas las ecuaciones que se muestran como opciones están en la forma general de la ecuación de segundo grado.
Entre todas, si se pretende factorizar el primer miembro de la ecuación de la opción “D”, se estarían buscando dos números que suman negativo 5 y cuyo producto es negativo 84, que es de las cuatro opciones, la más cercana a lo que se pide. La opción correcta es “D”.
Conviene apuntar que haber tenido numerosas oportunidades de enfrentar este tipo de ecuaciones, factorizando trinomios de segundo grado como producto de binomios con término común, te permitirá saber que los números que se buscan son 12 y 7 negativo.
Así es, 12 por 7 negativo es igual a 84 negativo. Y 12 más 7 negativo es igual a 5.
Es muy útil conocer las características de múltiplos y divisores, pues eso permite saber que una de las parejas de números que dan como resultado 84 son 12 y 7. Aunque también lo son 84 y 1, 42 y 2, 28 y 3, 21 y 4, junto con 14 y 6.
Si no cuentas con esos recursos, puedes ir desde lo básico y resuelve de manera formal.
Aunque se trata de dos números diferentes, las condiciones del enunciado los relacionan.

Para que la ecuación quede en términos de “x”, como aparece en las opciones, se despeja “y” en la segunda ecuación y se sustituye en la primera, quedando como “x”, por 5 menos “x” es igual a 84 negativo.
Una vez que se tiene la ecuación con una sola incógnita, se simplifica, se iguala con cero, y se pone en la forma general de la ecuación de segundo grado.
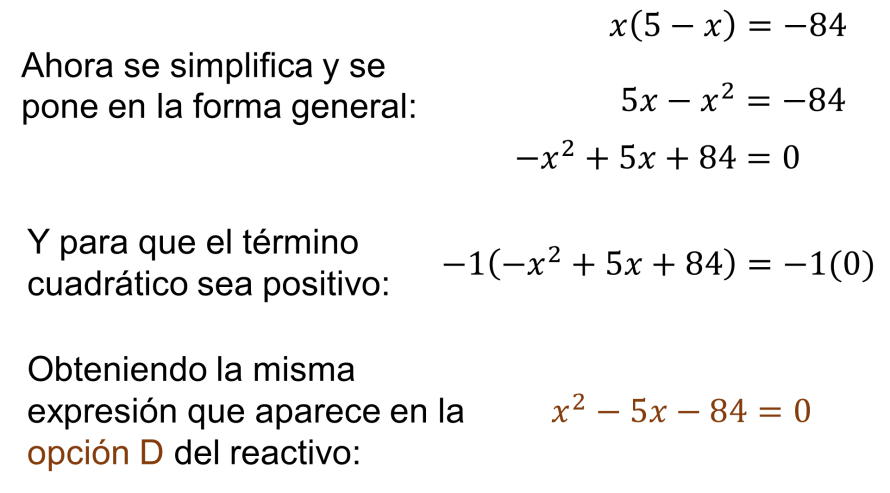
Para que el signo del término cuadrático sea positivo, se multiplican ambos términos de la ecuación por 1 negativo.
La expresión así obtenida es igual a la que se muestra en la opción “D” del reactivo.
“X” al cuadrado menos 5 “x” menos 84 igual a cero.
Para efectos de elegir la opción correcta del quinto reactivo, no hace falta continuar con el desarrollo de la solución y hallar las raíces de la ecuación, aunque si lo deseas lo pueden realizar por tu cuenta.
Un examen de opción múltiple de este tipo pone a prueba una estructura completa de conocimientos desarrollados a lo largo de un trayecto específico, la educación secundaria en este caso.
Por ello, no es extraño que las soluciones se simplifiquen en la medida que se dominan recursos matemáticos, adquiridos progresivamente a lo largo de los años y no solamente durante el tercer grado. Procura actualizar y consolidar tales recursos y saberes.

Tras leer el enunciado, se sabe que alguna de las ecuaciones propuestas como opciones tiene como raíces 3 y – 2.
A fin de utilizar recursos prácticos y optimizar el tiempo de respuesta, se propone una solución inversa.
Puede notarse que las ecuaciones están ordenadas en la forma general.
Se identifica que las expresiones en el primer miembro de las ecuaciones son trinomios de segundo grado que podrían ser factorizados como producto de binomios con término común.
Teniendo las raíces se pueden armar los binomios y al multiplicarlos hallar la ecuación.
Siendo así las raíces 3 y 2 negativo son los simétricos de los términos no comunes de los binomios con término común en que se factoriza la ecuación. Es decir, los binomios son “x” menos 3 y “x” más 2. El término común es “x”, y al multiplicarlos se obtiene el trinomio que aparece en la ecuación de la opción “A”, “x” al cuadrado menos “x” menos seis igual a cero.
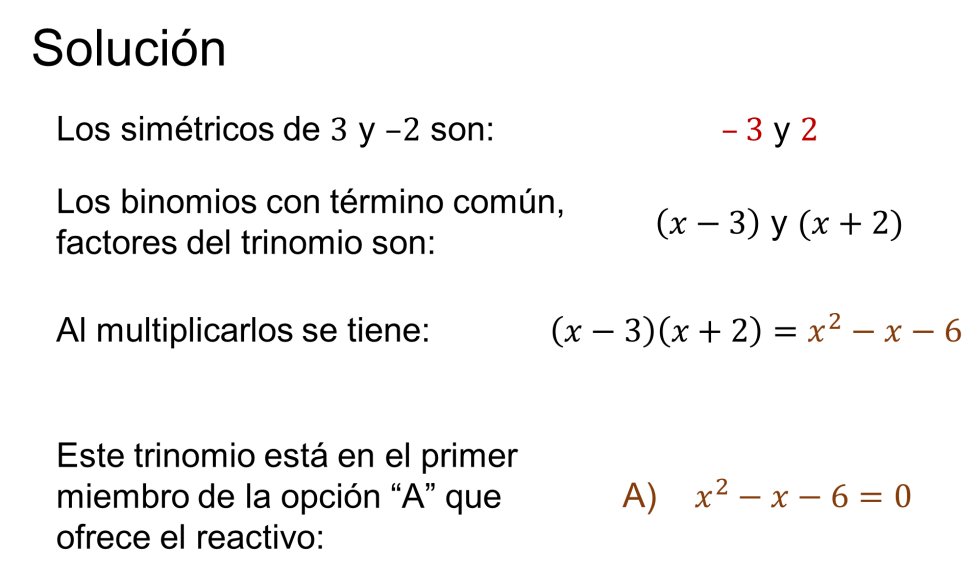
Una vez más se hace evidente el que las soluciones se abrevian en la medida de los recursos y habilidades que tengas para resolverlos.
Para el reactivo anterior, es preponderante el conocimiento de los productos notables, sus características y su factorización.
Sin embargo, también es una opción intentar resolver las ecuaciones de las opciones, ya sea por factorización o por fórmula general. La desventaja en este tratamiento es que no siempre resulta ser la correcta la primera opción. Y tal vez necesites resolver dos o tres ecuaciones antes de hallar la opción correcta.

Después de leer con atención, se entiende que no hay que calcular las edades de Julián y Mariana, ni resolver la ecuación. Únicamente debes encontrar la ecuación. Traducir el enunciado del lenguaje común al lenguaje algebraico es la mejor manera de abordar el reactivo.
Las incógnitas están en términos de las iniciales de Julián y Mariana: “j” y “m”. Pero la ecuación cuadrática debe estar en términos de una sola incógnita, por lo que se indica la edad de Mariana en términos de la edad de Julián.
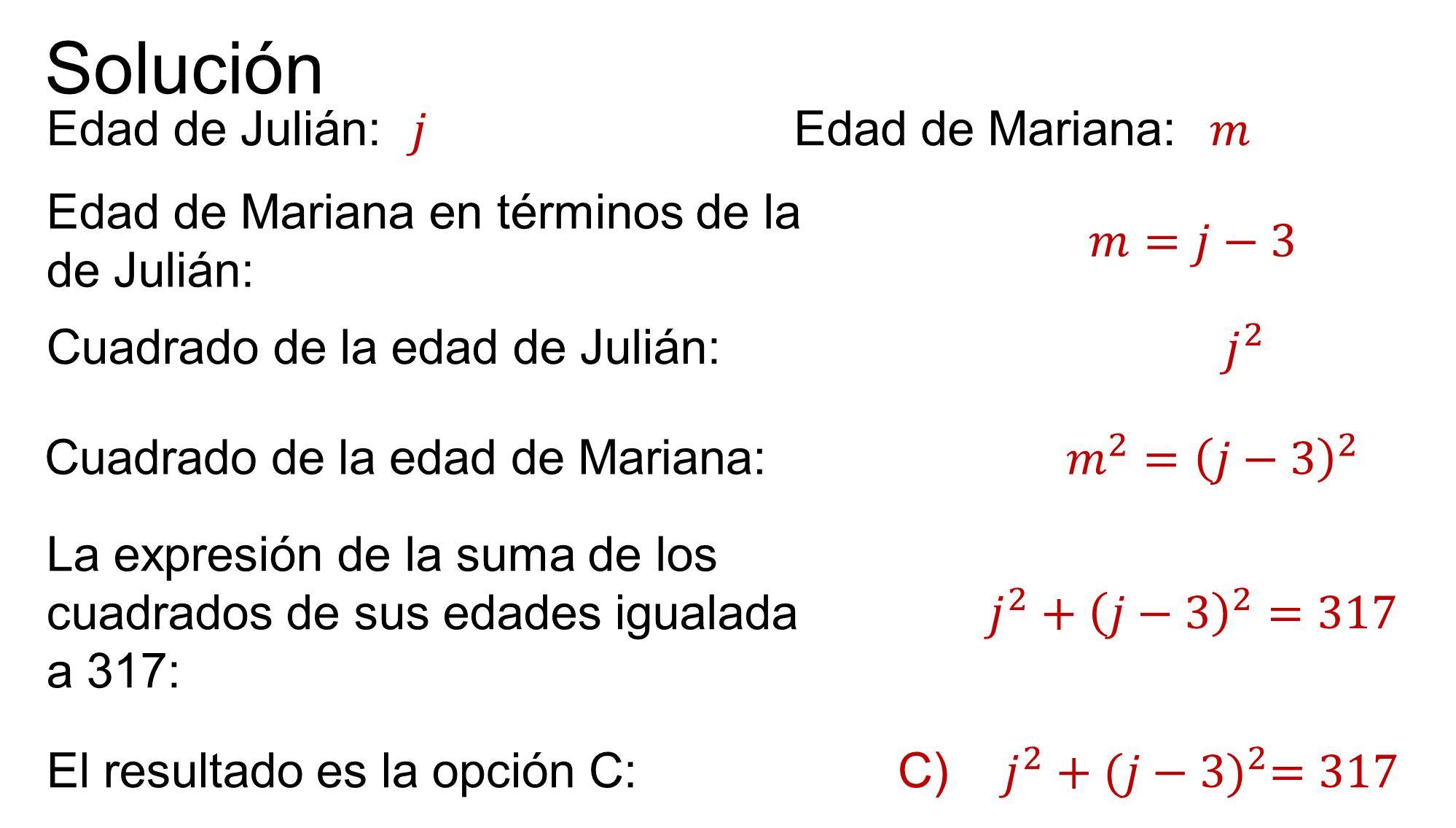
Si la edad de Julián es “j”, la edad de Mariana es “j” menos 3. Porque Julián tiene 3 años más que Mariana.
Se escribe la expresión de acuerdo con el enunciado.
El cuadrado de la edad de Julián “j” al cuadrado, más el cuadrado de la edad de Mariana, “j” menos 3 al cuadrado, igual a 317.
Corresponde a la opción “C” del reactivo.
Cada reactivo en el que han conseguido el éxito al elegir la opción correcta aumenta su seguridad y mejora su disposición al enfrentar este tipo de pruebas.
Según te sea posible, consigue guías de estudio y ensaya pruebas interactivas.
Realiza un compendio con pequeñas notas y sugerencias que te sirvan de ayuda al prepararse para el examen.
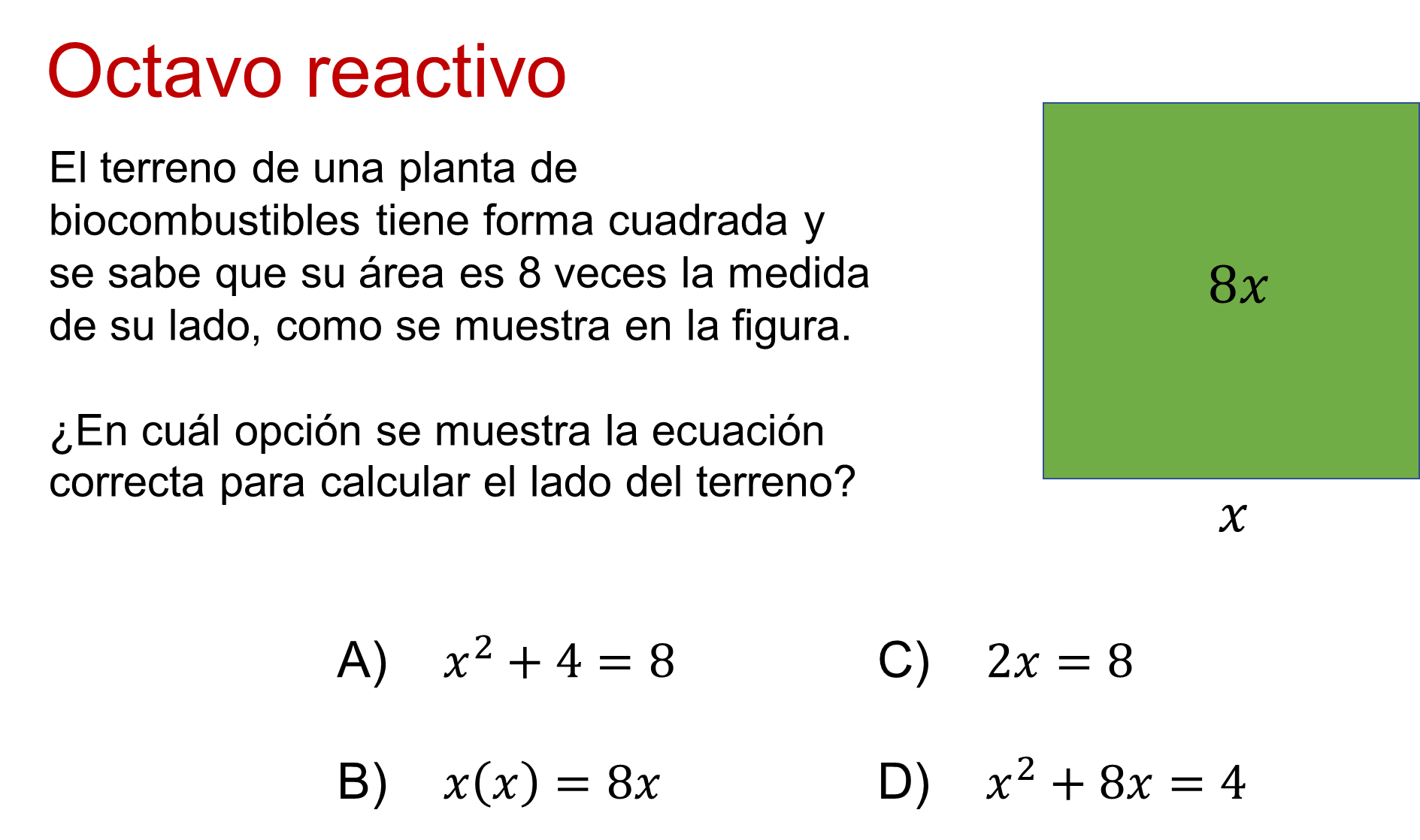
El enunciado indica que el terreno es cuadrado, y como la medida del lado se representa con “x”, el área de dicho cuadrado es “x” por “x” o “x” al cuadrado. Esa expresión se iguala con 8 “x”, es decir, 8 veces la medida del lado.
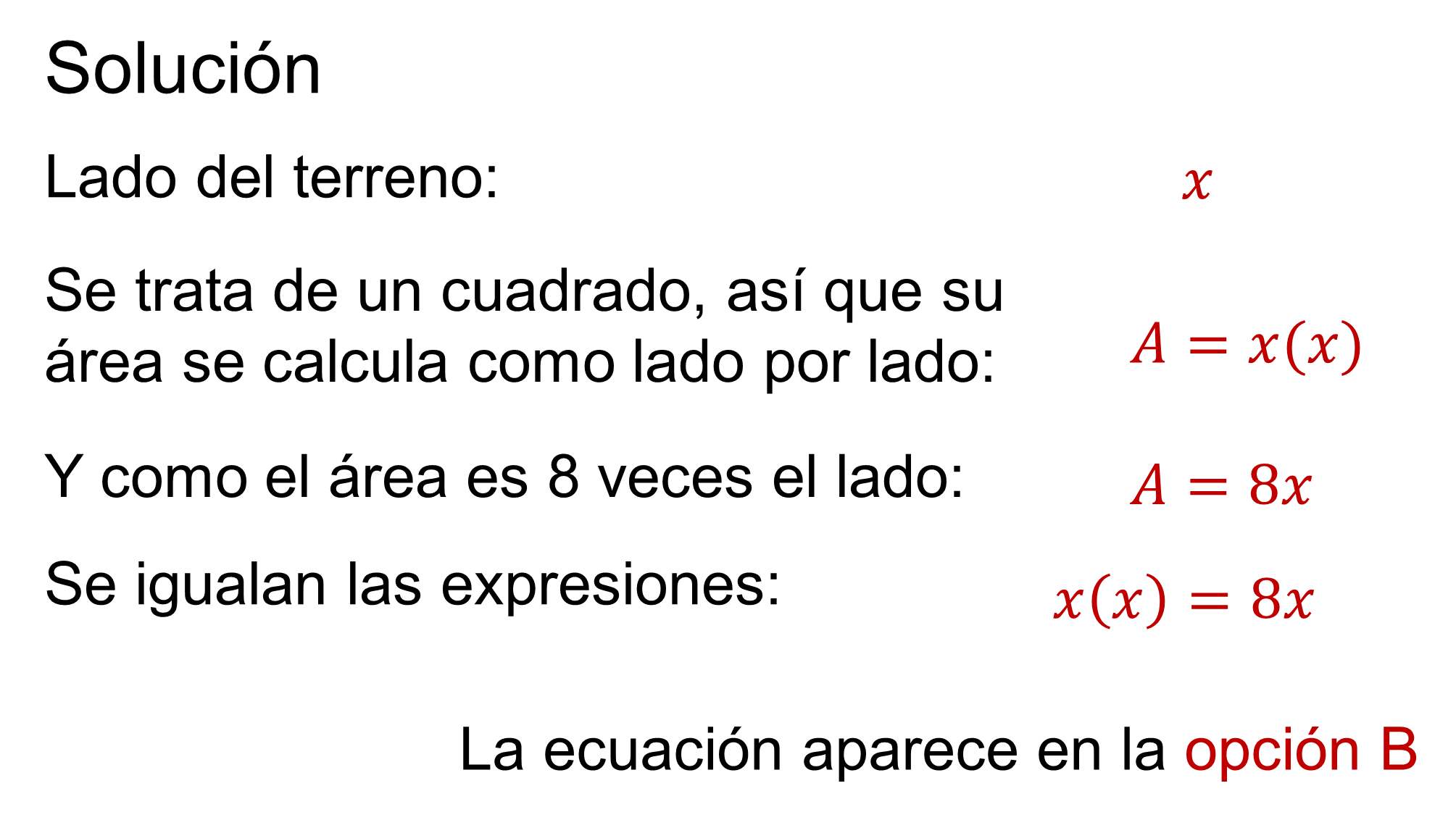
Desde luego, el criterio para decidir qué recursos deben emplearse al resolver este tipo de reactivos se desarrolla con el tiempo y la práctica, así que busca frecuentes ocasiones para ejercitar tu habilidad y conocimientos en matemáticas.
La intención de las herramientas y sugerencias aprendidas es contribuir al éxito que puedes alcanzar al resolver las pruebas escritas de opción múltiple.
Siempre que te sea posible, comparte tus anotaciones con tus compañeros y tu maestra o maestro. Seguramente, socializar tus conjeturas resultará de gran utilidad para apropiarse de recursos, habilidades y conocimientos muy valiosos en este tipo de evaluaciones.
El reto de hoy:
Localiza en las páginas de tu libro de texto las secciones de autoevaluación que aparecen al final de cada bloque. Ponte a prueba intentando resolver los reactivos que te ofrecen.
En caso de que no cuentes con el libro, tienes la opción de consultarlo en la página de la Comisión Nacional de Libros de Texto Gratuitos.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.