Resolución de problemas integradores. Manejo de la información II
Resolución de problemas integradores. Manejo de la información II
Aprendizaje esperado: desarrollar habilidades que le permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Énfasis: consolidar la resolución de problemas. Manejo de la información II
¿Qué vamos a aprender?
Es importante que conforme se vayan presentando las distintas actividades y ejercicios las vayas, realizando, así como tomar notas en tu cuaderno de lo que aprendes.
Irás paso a paso identificando, reflexionando y practicando las diferentes maneras de resolver problemas del eje manejo de la información.
Entre los temas que abarca el eje están la proporcionalidad y funciones, nociones de probabilidad, así como el análisis y representación de datos.
Se te sugiere tener a la mano cuaderno, regla, lápiz o bolígrafo y lápices de colores.
Para el desarrollo de esta sesión es importante tener presente cómo resolver problemas y analizar la pregunta junto con cada respuesta posible.
Cada vez que se te presente un problema primero intenta comprender que está preguntándote y así empezar a contestarlo.
Es necesario que prestes mucha atención para seguir cada pregunta.
¿Qué hacemos?
Durante la sesión se presentarán 9 preguntas; anota tus respuestas para verificar o modificar, si es necesario.
Es relevante que analices la forma en que puedes responder para que lo apliques en los siguientes retos al finalizar tu educación secundaria.
Pregunta 1.

Si se tienen 100 canicas y sólo 8 son rojas, entonces la probabilidad de que obtenga una canica roja es de 8 sobre 100, esa puede ser la respuesta. Pero la pregunta dice sacar una al azar que no sea roja, por lo tanto, la respuesta es el complemento de 8 sobre 100, que es 92 sobre 100.
Las otras respuestas no representan lo que plantea el problema.
Es importante que leas cada problema las veces que sea necesario y hacerse la pregunta, al analizarla qué es lo que se está solicitando para verificar cada opción de respuesta.
Pregunta 2.
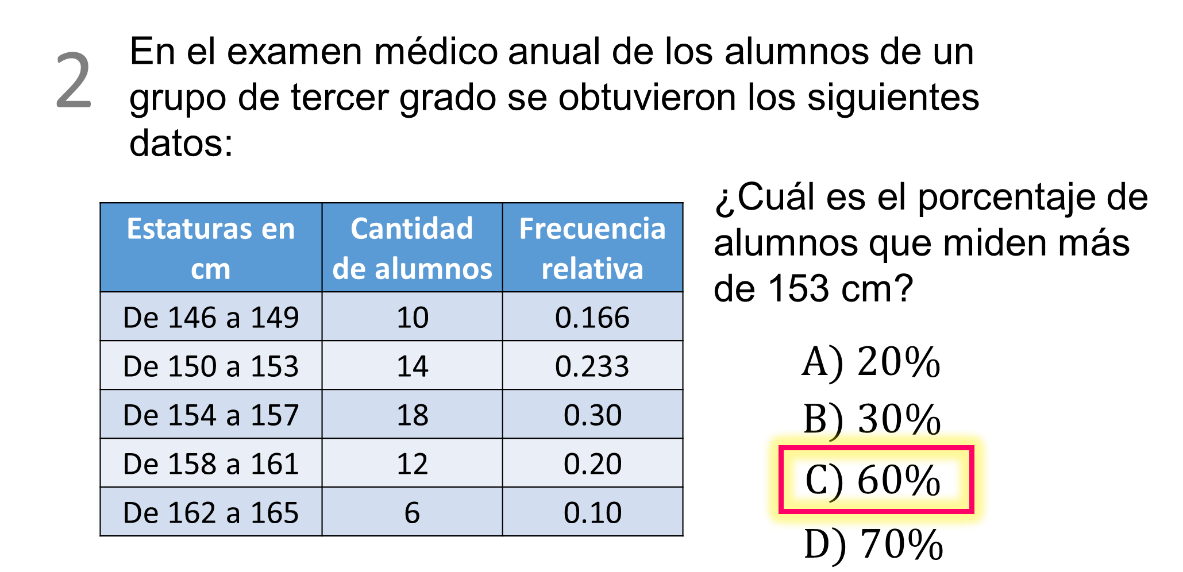
Relee el problema, se solicita el porcentaje de alumnos, pero en la tabla sólo aparece la frecuencia relativa, que se expresa en número decimal.
Si se suman las frecuencias relativas tienes casi la unidad, aproximadamente 0.99 en este caso, entonces debes obtenerlo en porcentaje multiplicando por 100 los números decimales, pero sólo de los que tienen una estatura de más de 153 centímetros.
Por lo tanto, 0.30 por 100 es igual a 30, 0.20 por 100 es igual a 20 y 0.10 por 100 es igual a 10. Así que 30 más 20 más 10 es igual a 60.
Entonces la respuesta es 60%, inciso “C”, descartando así las demás opciones.
La frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos, que en este caso ya estaban en la tabla, sólo había que encontrar los porcentajes correspondientes para los alumnos de más de 153 centímetros de estatura.
Pregunta 3.
Si se lanzan 2 dados con sus caras numeradas del 1 al 6, uno es rojo y otro azul, y se suman los puntos que aparezcan, ¿de cuántas formas diferentes pueden aparecer los puntos de los dados?
Inciso a, 6
Inciso b, 12
Inciso c, 18
Inciso d, 36
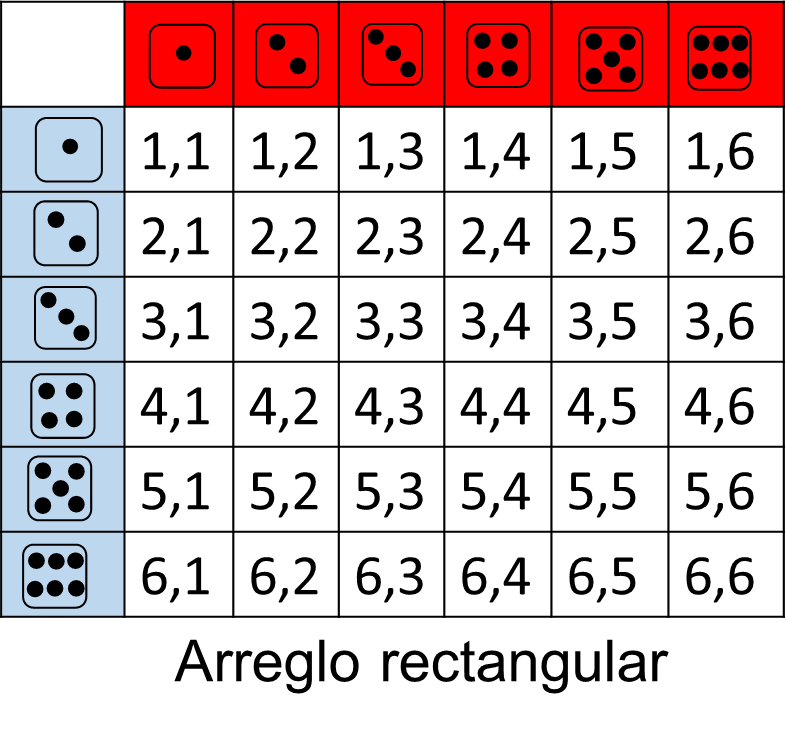
En este caso se tienen 2 dados y cada uno tiene 6 números posibles que pueden caer y cada uno se puede combinar con 6 opciones del otro dado, por lo tanto 6 por 6 es igual a 36 formas diferentes en que pueden aparecer los puntos.
La respuesta es el inciso “d”.
El color de los dados en este caso no influye en el resultado.
Otras formas de resolver esta pregunta, es jugar directamente con los dados para saber las combinaciones, pero también se puede construir un diagrama de árbol o un arreglo rectangular para generar todas las formas posibles.
Tu respuesta es correcta.
Pregunta 4.
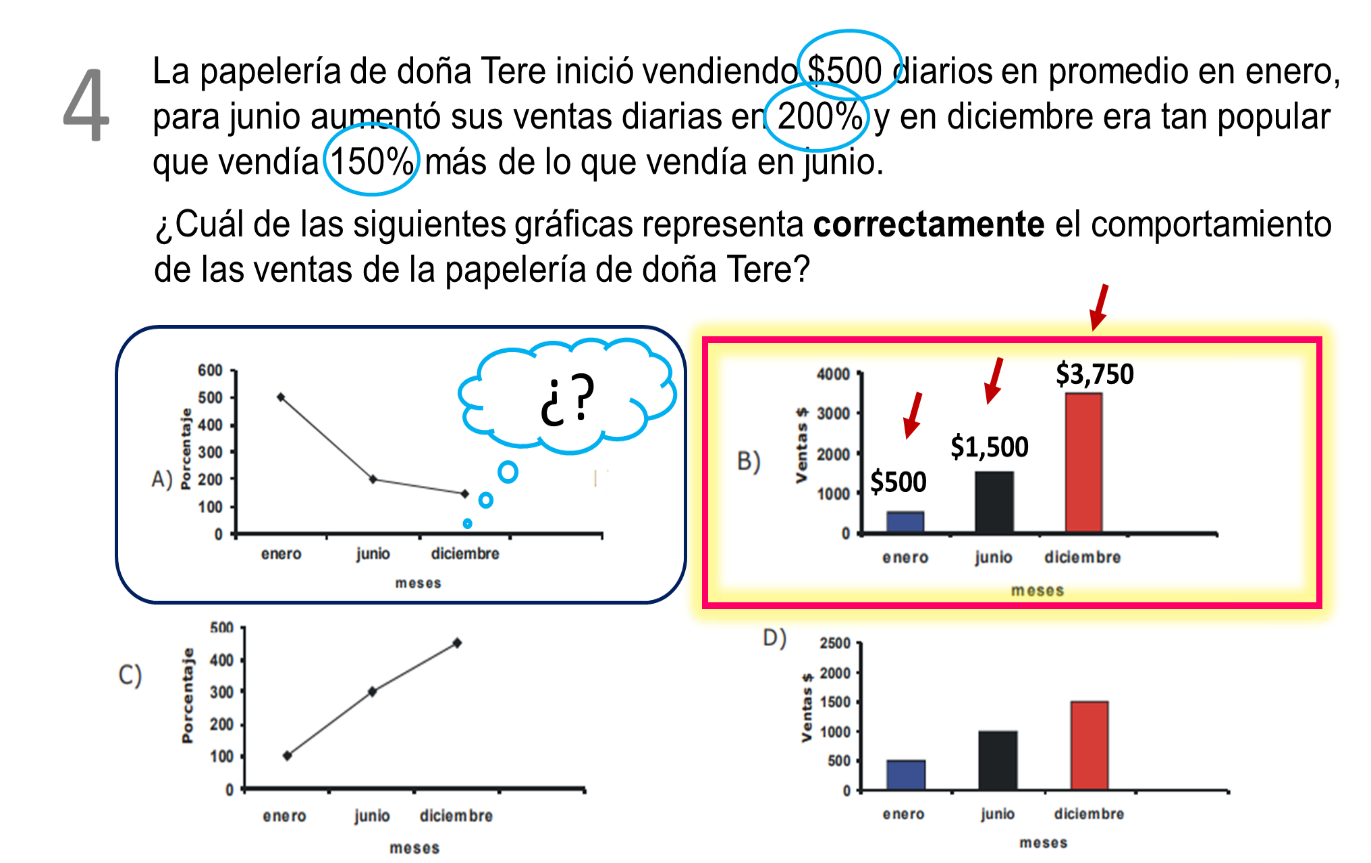
Como puedes observar, en cada inciso hay una gráfica para representar la situación, debes analizar cuál es la correcta.
Releyendo la situación y observando las gráficas, es el inciso “a”, ya que en esta gráfica se observa marcada cada cantidad que aparece en el texto del problema y los porcentajes mencionados.
En esta ocasión no es la respuesta correcta.
Faltó reflexionar el contenido de la pregunta, se escogió la que parece adecuada sin hacerlo, también me faltó observar detalladamente las gráficas. Y hacer operaciones para ver las cantidades en cada gráfica.
Reflexionando, el inciso “a” y el inciso “c” quedan descartados, ya que la pregunta se refiere a las ganancias y no al porcentaje de aumento en las ventas.
Se ha descartado de forma adecuada con sólo analizar nuevamente la pregunta.
Contestando a la pregunta, las cantidades que aparecen son 500 pesos diarios para las ventas en enero, luego aumentó esa cantidad en un 200%, es decir $1 000, entonces a finales de junio vendía $1 500 al día, y el 150% de esa cantidad es de $2 250, por lo tanto, las ventas diarias en diciembre fueron $3 750.
Por lo tanto, la gráfica correcta es la del inciso “B”, y queda descartado el inciso “D”, ya que el total de las ventas no se calculó correctamente.
Es importante darse un tiempo para analizar cada pregunta. Hacerlo de manera precipitada puede ocasionar que no se acierte en este tipo de preguntas.
Pregunta 5.
Su contenido tiene que ver con medidas de tendencia central.
“Halla el promedio de las siguientes cantidades: 9, 13, 17, 10, 11”.
Inciso “a”, 6.
Inciso “b”, 12.
Inciso “c”, 16.
Inciso “d”, 60.
Para resolver se tiene que calcular el promedio, entonces suma los datos que se proporcionan y lo que se obtiene dividirlo entre el número de datos totales.
Haciendo un análisis de las respuestas se observa que en el inciso “a” y el “d” no hay valores cercanos a esas cifras y quedan descartados.
Calcula mentalmente, 13 más 17 es igual a 30, más 10 igual a 40, más 11 igual a 51 y por último más 9 dando como resultado 60.
Entonces 60 entre 5 es igual a 12.
Por lo tanto, la respuesta es el inciso “b”.
Analiza algunas herramientas para resolver problemas matemáticos. Es conveniente detenerte para reflexionar y tomar nota de lo que se ha realizado.

Con las herramientas del filtro de problemas se puede contestar de mejor manera cada pregunta, ponlas en práctica con más ejercicios.
Realiza más preguntas del eje temático “Manejo de la información”.
Pregunta 6.
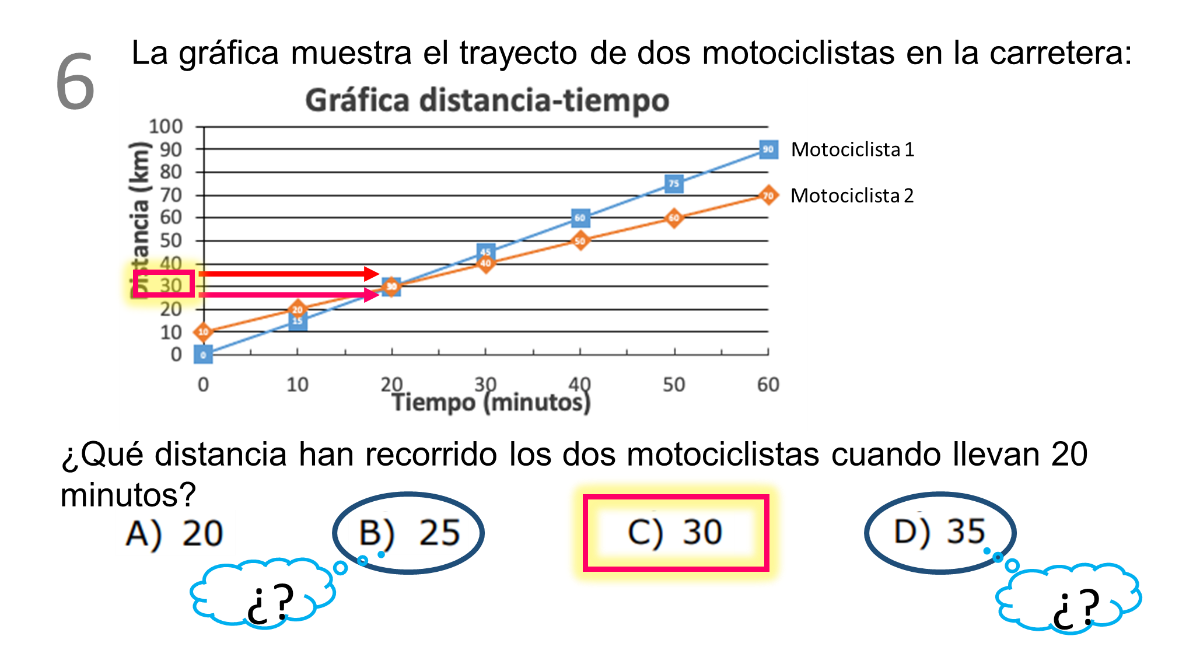
Se observan ambas rectas y cómo avanzan en kilómetros con respecto al tiempo transcurrido, el automovilista 1 comienza en 10 km y el 2 en 0 km.
Se pregunta solamente cuánto recorrieron ambos a los 20 minutos.
Considera que en el eje horizontal se representa el tiempo y en el vertical la distancia en km. Así que al observar las rectas que representan el desplazamiento de los dos automóviles, se puede ver que es cuando las rectas se intersecan, por lo tanto, la respuesta correcta es 30 kilómetros, es decir el inciso “c”, ya que es justo donde ambas rectas se cortan cuando transcurrieron 20 minutos.
Respuesta correcta.
Se puede hacer notar que no es relevante que ambas rectas coinciden. Sin embargo, en esta gráfica, se puede ver que los vehículos llevan diferentes velocidades y que al minuto 20 ambos han recorrido 30 km.
Toma nota, verifica y modifica tus respuestas de ser necesario.
Lo más relevante es que puedes darte cuenta de cómo se puede ir resolviendo una prueba que involucra habilidades del pensamiento, conceptos, comprensión lectora y pensamiento matemático para el manejo de la información que se presenta.
Analiza la siguiente pregunta.
Pregunta 7.
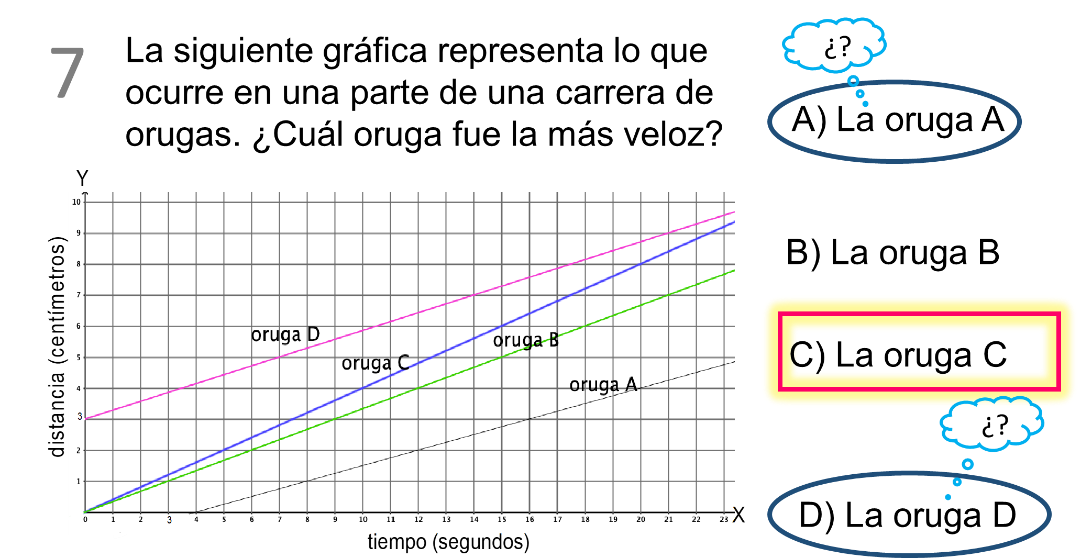
Parece un poco difícil poder contestar, pero observando la gráfica se puede ver que, en el eje horizontal (x), tienes los segundos y en el eje vertical (y) la distancia en centímetros, eso quiere decir que la inclinación de cada segmento de recta puede decirte la respuesta.
¿Hacia dónde indicará la inclinación la mayor velocidad?, ¿cuándo se acerca al eje (x) o cuándo se aleja?
Pues en este caso cuando el segmento de recta se aleja del eje (x), ya que así avanza más distancia en menos tiempo y al contrario, entre más cerca del eje de los segundos (x) hará más tiempo y menos distancia.
Por ejemplo, en el caso del segmento de recta de la oruga “A” la recta se inclina al eje (x), aunque se observa más arriba de todas si nos imaginamos la prolongación de la misma, nos damos cuenta de que no es la más veloz, lo mismo ocurre con la recta de la oruga “D”.
De esta forma quedan los segmentos de las rectas de la oruga “B” y la oruga “C”, y siguiendo la deducción anterior la más veloz es la oruga “C”, ya que el segmento de recta tiende a inclinarse hacia el eje “Y” con lo cual recorre más distancia en menos tiempo.
Por lo tanto, la respuesta es que la oruga más veloz es el inciso “C”.
Las observaciones de la gráfica son pertinentes y es la respuesta correcta, pero puedes analizar otro procedimiento para obtener un resultado correcto también.
Mediante el uso de la razón de cambio, ya que es un concepto útil al estudiar relaciones funcionales lineales porque permite analizar el cambio relativo de una variable con respecto a otra.
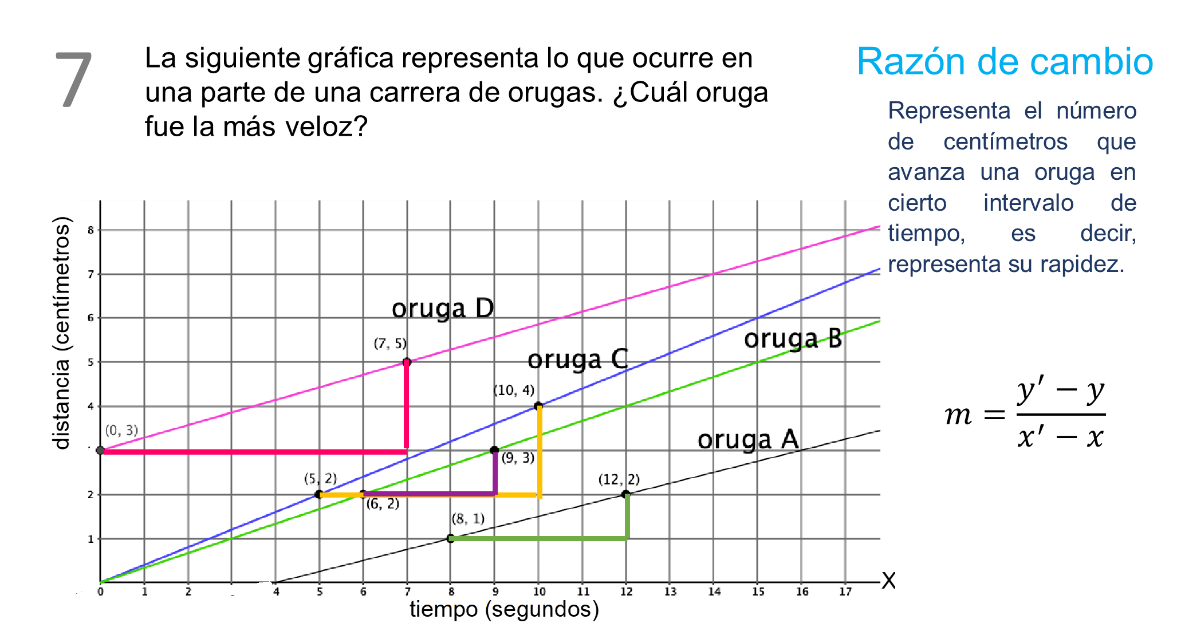
La razón de cambio que también es la pendiente de cada recta en este caso representa el número de centímetros que avanza una oruga en cierto intervalo de tiempo, es decir, representa su rapidez.
Analiza la recta que representa el desplazamiento de cada oruga.
No todas las orugas empezaron la carrera en el punto (0,0), lo cual no tiene relación directa con la razón de cambio.
A una mayor razón de cambio, mayor inclinación de la recta con respecto al eje “Y”.
La forma de obtener la razón de cambio entre dos puntos (x,y) y (x´, y´) que pertenecen a una recta es: y´-y sobre x´-x
Las razones de cambio asociadas al movimiento de cada oruga son:
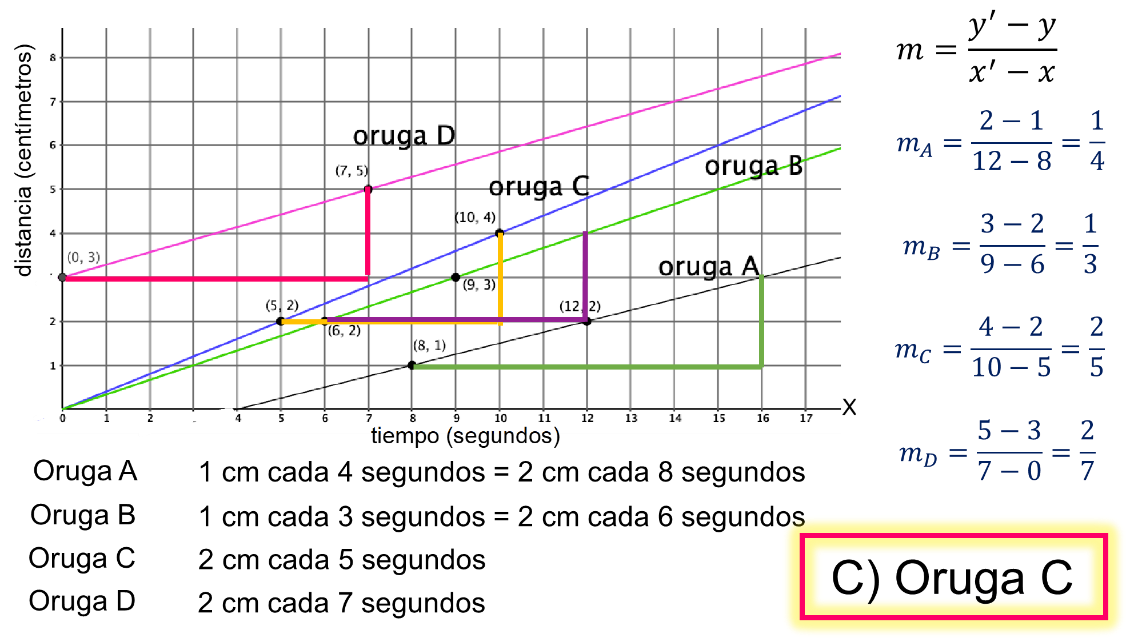
Por lo tanto, la oruga “C”, que avanzó 2 cm en menos tiempo es la más veloz, siendo el inciso “C” la respuesta correcta.
Interesante forma de resolver la pregunta anterior, hay varios procedimientos para tomar en cuenta.
Justamente, hay que considerar las diversas herramientas para afrontar cada pregunta, pero la principal es el conocimiento del tema al que hace referencia cada cuestión.
Observa los últimos 2 problemas de la sesión.
Pregunta 8.

La respuesta es el inciso “a”, ya que tienes 6 combinaciones de números que pueden caer igual al tirar los dados, por lo tanto 6 números favorables de los 36 posibles.
Teniendo en cuenta las herramientas del filtro de problemas faltó que le preguntarás a la pregunta, ya que tu respuesta está considerando que al lanzar los dados caigan el mismo número en pareja.
Es cierto la pregunta dice que NO caigan ambos dados el mismo número, lo contrario a lo que se hizo. Pero también ayuda a la respuesta.
Ciertamente, ya que, al considerar esa respuesta, el resto de los casos que al tirar los dados no caiga el mismo número, se calcula con la probabilidad de un evento simple.
La probabilidad de un evento “A”, es igual al cociente entre el número de casos favorables y número de casos posibles.
Por lo tanto, la respuesta es 30/36, donde 30 son el total de combinaciones que pueden caer diferentes números en cada dado, y 36 el número posible de combinaciones, siendo correcto el inciso “b”.
Por eso es conveniente leer muy bien cada instrucción en una prueba con diversas preguntas y también debes considerar el filtro de problemas que has practicado durante la sesión.
En ocasiones debes releer y evaluar la pertinencia de los resultados regresando a analizar la pregunta, puedes comprobar si la respuesta cumple correctamente lo que pide el cuestionamiento.
En la pregunta se pudo descartar los incisos “c” y “d”, ya que tienen como casos posibles 12, eso lo puedes observar en su denominador, cuando al tener dos dados y lanzarlos el número de eventos posibles se calcula multiplicando 6 por 6 para obtener el total.
El análisis tiene un grado de error, si observas la respuesta que se ha marcado como correcta, en este caso 30 sobre 36avos, puede simplificarse a una fracción con denominador 12, que sería 10 sobre 12avos, lo que te hace ser cuidadoso en tu análisis.
En preguntas que se utilizan en modelos de selección de personal o de ingreso a una institución escolar, también se evalúa en la misma algunos otros contenidos.
En este caso la equivalencia de expresiones fraccionarias es una de ellas. Así las respuestas de esta pregunta pudieron estar expresadas todas en doceavos, lo que implicará realizar la simplificación de las fracciones dadas.
Analiza la última pregunta.
Pregunta 9.
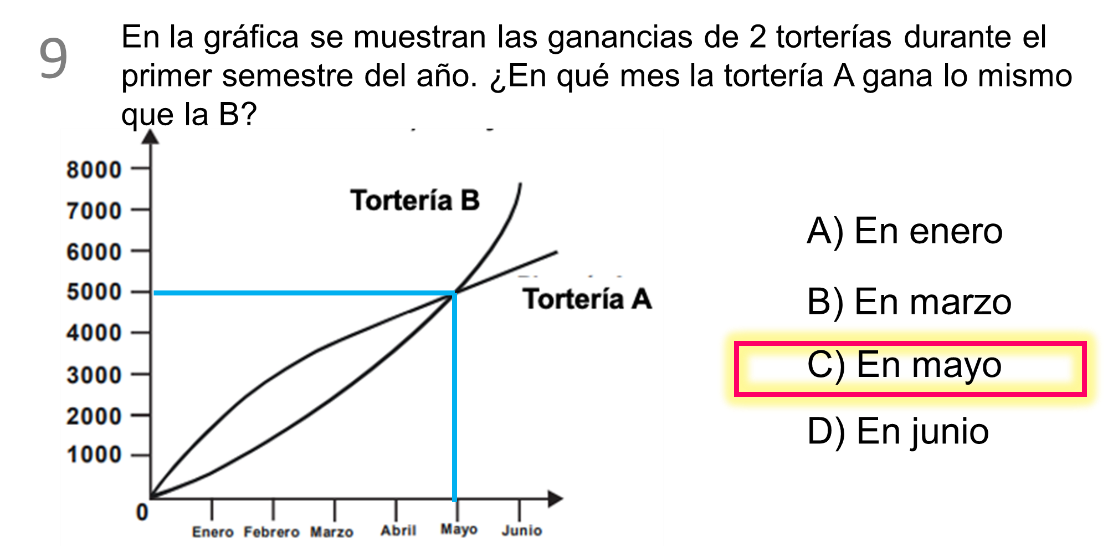
Implementa las herramientas del filtro de problemas. Por lo tanto, la pregunta que debes averiguar es, en qué mes ambas torterías ganan lo mismo.
En la gráfica se observa que en los meses de enero a abril varían sus ganancias una de la otra. Por consiguiente, descarto el inciso “A” y “B”.
Así que donde se cruzan las líneas es el punto donde obtuvieron la misma ganancia, entonces la respuesta correcta es el inciso “C”.
Dentro del análisis y representación de datos, cuando dos líneas se intersecan, significa que los valores para ese punto son iguales. En el ejercicio, representan que en ese mes las torterías coinciden en la misma cantidad de ventas, justo como lo mencionas, es el punto donde son exactamente iguales, esto quiere decir que de acuerdo con la gráfica el mes de mayo corresponde a esta descripción.
Es importante que desarrolles habilidades que te permitan plantear y resolver problemas usando las herramientas matemáticas.
A través de la rutina de pensamiento llamada filtro de problemas para tomar decisiones y enfrentar situaciones no rutinarias, puedes afianzar tus habilidades.
El reto de hoy:
Para resolver dudas o ejercitar lo aprendido te puedes apoyar en tu libro de texto, en caso de que no cuentes con él, lo puedes encontrar en internet la página de la Comisión Nacional de Libros de Textos Gratuito.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.