Resolución de problemas integradores. Forma, espacio y medida I
Resolución de problemas integradores. Forma, espacio y medida I
Aprendizaje esperado: desarrolla habilidades que le permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Énfasis: resolver problemas integradores. Forma, espacio y medida.
¿Qué vamos a aprender?
Los materiales que utilizarás en esta sesión son tu cuaderno de apuntes, bolígrafo, lápiz, goma, colores y regla o escuadra. En el momento que consideres necesario, consulta tu libro de texto.
Es importante analizar que, para resolver problemas o retos hay una infinidad de formas o caminos de solución, pero previo a hacer números u operaciones debes considerar que tienes una organización al momento de buscar un resultado, puesto que, si no comprendes bien y te guías por conjeturas, puedes llegar a un resultado erróneo.
Por lo anterior, es recomendable seguir estrategias o procesos para resolver problemas o retos matemáticos.
Como puede ser el método de cuatro pasos de George Polya.
George Polya fue un matemático húngaro, que a través de su libro “How To Solved It “Como se resuelve”, abordó este tema, sobre los pasos para resolver un problema.

Los primeros pasos son:
Paso 1: Comprender el problema, es decir, entender que piden calcular. Analizar y leer cuidadosamente el problema o reto para determinar: ¿qué debo calcular?
Paso 2: Ubicar y designar la o las incógnitas del problema, de acuerdo con los datos proporcionados identificar cual o cuales son las incógnitas del problema.
Paso 3: Elaborar un plan, identificando los datos que se proporcionan para idear una estrategia de solución a través del uso de esquemas, formulas, operaciones matemáticas, sentido común, entre otras.
Paso 4: Aplicar el plan, que es poner en práctica la estrategia elegida, dando el tiempo necesario para resolver el reto o problema e incluso si es necesario volver a empezar.
Paso 5: Revisar y verificar el resultado, analizar si la respuesta es razonable, si contesta lo solicitado en el reto o si es posible resolverlo de otra manera.
Se te sugiere consultar el libro antes citado para profundizar en el tema.
Ya que se ahí se aborda de forma general como resolver retos o problemas.
Inicia con el planteamiento de algunos ejercicios para poner en práctica lo analizado.
Considerando que en la sesión resolverás ejercicios del eje: Forma, espacio y medida. Estos se presentan con 5 opciones posibles de resultado, de las que se elegirás la correcta.
Puedes tomar nota de los ejercicios retos y resultados para tu posterior análisis.
¿Qué hacemos?
Inicia con un ejercicio sobre rectas y ángulos: tienes dos rectas paralelas cortadas por una secante, formando 8 ángulos.
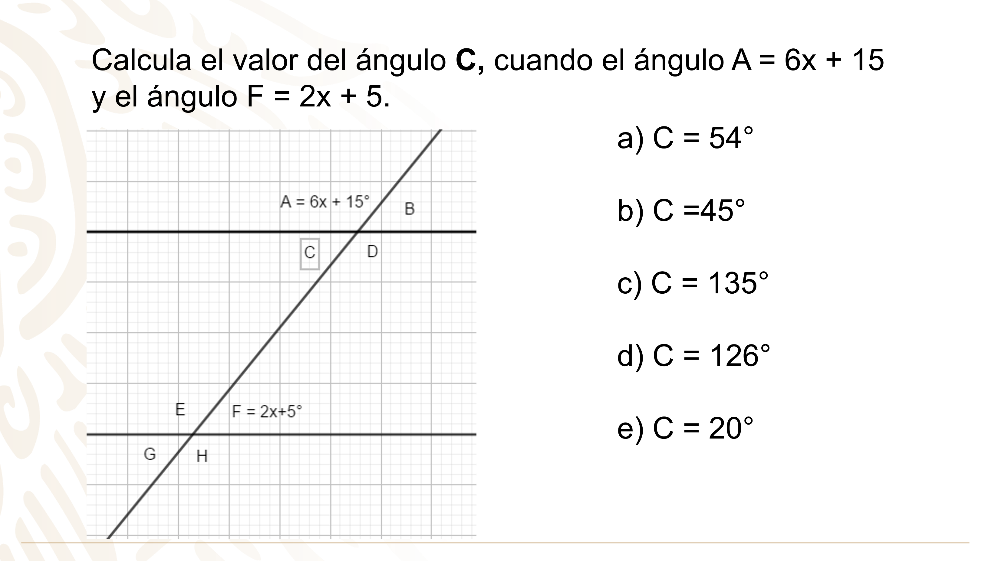
Observa la relación entre los 8 ángulos antes de resolver el ejercicio.
Es decir, primero debe quedar claro, ¿qué se solicita?
Para calcular el valor del ángulo “C” partes de conocer que cada ángulo con su contiguo o adyacente suman 180°, es decir, son suplementarios, por lo tanto:
El ángulo “A” más el ángulo “B” suman 180°, así como el ángulo “A” más el ángulo “C” suman 180°.
Lo mismo sucede con los otros ángulos adyacentes, por ejemplo, el ángulo “D” al sumarlo con el ángulo “B” o con el ángulo “C” suman 180°.
Y ocurre igual con los ángulos de la paralela de abajo, es decir, el ángulo “F” más el ángulo “E” o “H” suman 180° y así sucesivamente con los demás ángulos, siempre y cuando se sumen los ángulos adyacentes.
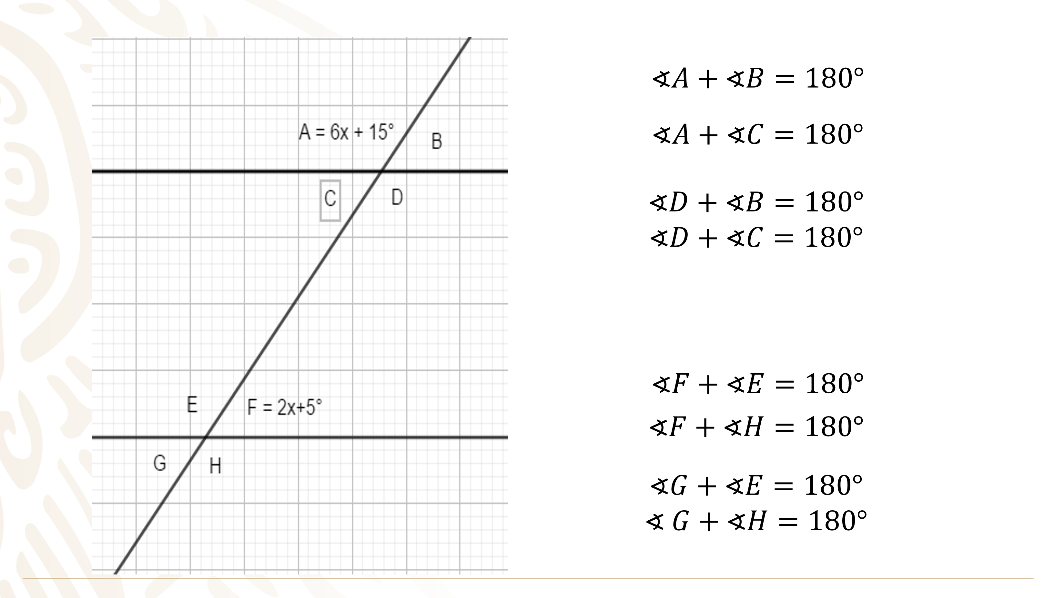
Si además tienes presente la correspondencia que existe entre los ángulos de las paralelas, es decir, la relación de igualdad entre los ángulos de la paralela de arriba con los ángulos de la paralela de abajo.
Puedes concluir que:
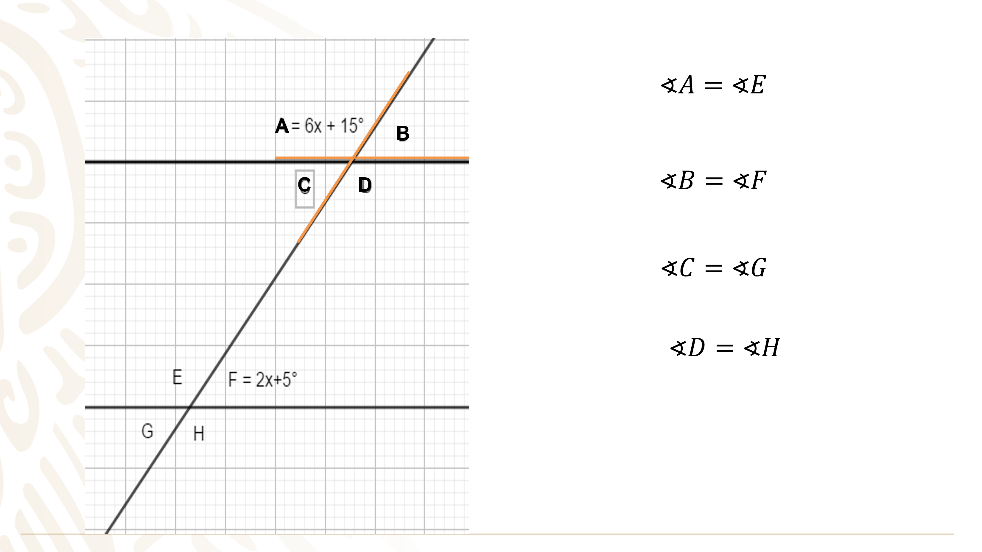
Por lo tanto, puedes seguir como estrategia de solución la combinación de los dos conceptos anteriores:
Si la suma de los ángulos “E” y “F” es 180° y el ángulo “A” es igual al ángulo “E” por ser correspondientes, puedes sustituir entonces, y el ángulo “A” más el ángulo “F” también suman 180 grados.
Sustituyes los valores del ángulo “A” que es igual a 6x más15, más el ángulo “F” que es igual a 2x más 5, y suman 180 grados.
Observa que se obtiene una ecuación de primer grado, que al simplificar tienes que 8x más 20 es igual a 180.
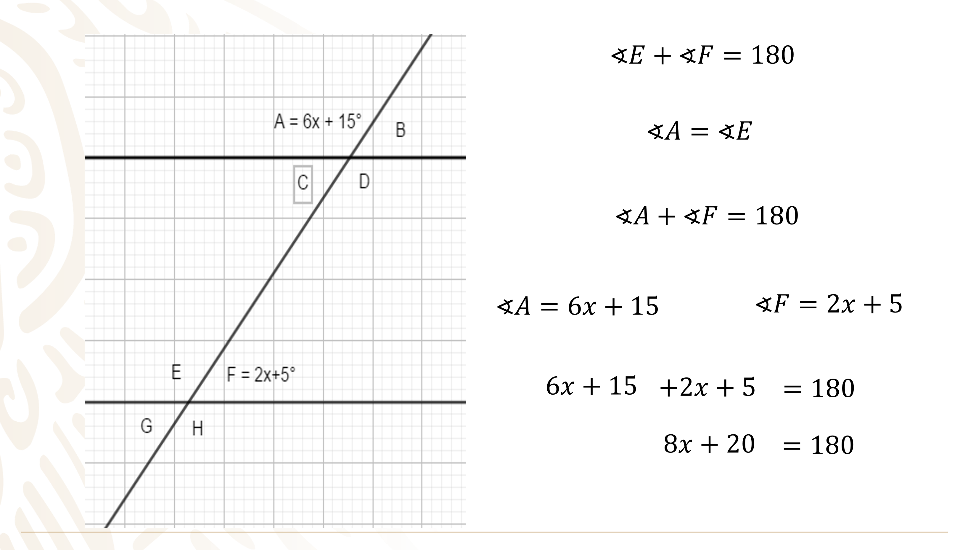
Se resta 20 en ambos miembros de la igualdad y tienes 8x más 20 menos 20 igual a 180 menos 20, se realizan operaciones y tienes 8x igual a 160.
Se divide entre 8 a ambos miembros de la igualdad, tienes 8x entre 8 igual a 160 entre 8, se realizan operaciones y tienes que “x” es igual a 20 grados.
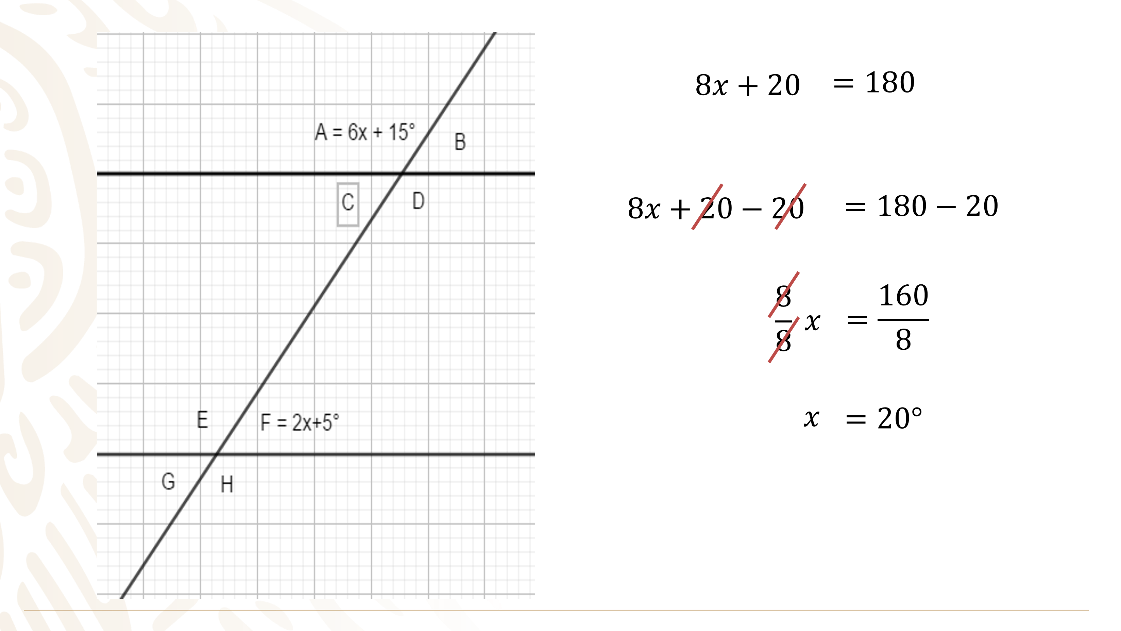
Este resultado se encuentra dentro de las opciones del ejercicio, pero no es lo que se solicita, porque preguntan el valor del ángulo C.
El ángulo “C”, es el suplementario del ángulo “A”, entonces se calcula el ángulo “A”.
El ángulo “A” es igual a 6x más 15, sustituyendo el valor de “x”, tienes que 6 por 20 más 15 es igual a 120 más 15 igual a 135 grados.
Si el ángulo “C” es el suplementario de “A”, es decir, suman 180° y el ángulo “C” son los grados que faltan para completar los 180°, entonces el ángulo “C” es 180 grados menos 135 grados, por lo que el ángulo “C” es igual a 45°.
Que es la opción b, del reactivo.
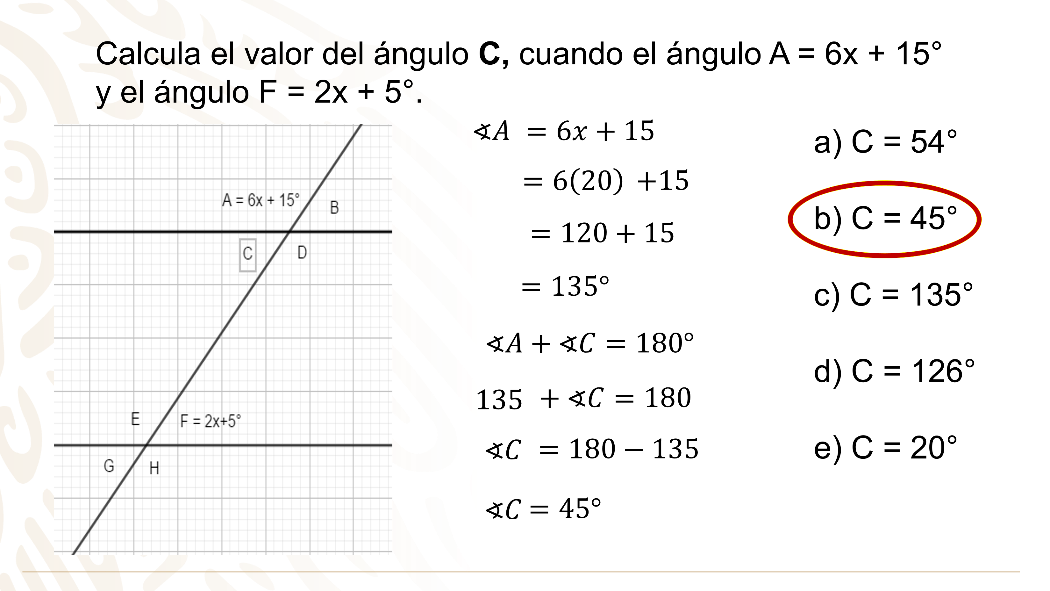
Existen ejercicios que manejan más de un tema para su solución. Como el ejercicio anterior que utilizó para su solución una ecuación lineal para conocer los grados de los ángulos entre las paralelas y la secante.
Ahora analiza el siguiente ejercicio:
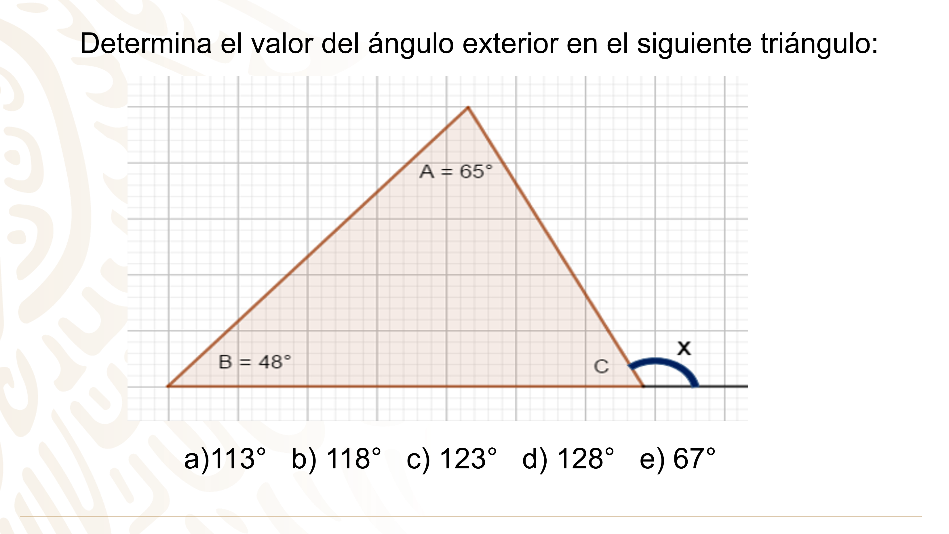
Los resultados posibles son:
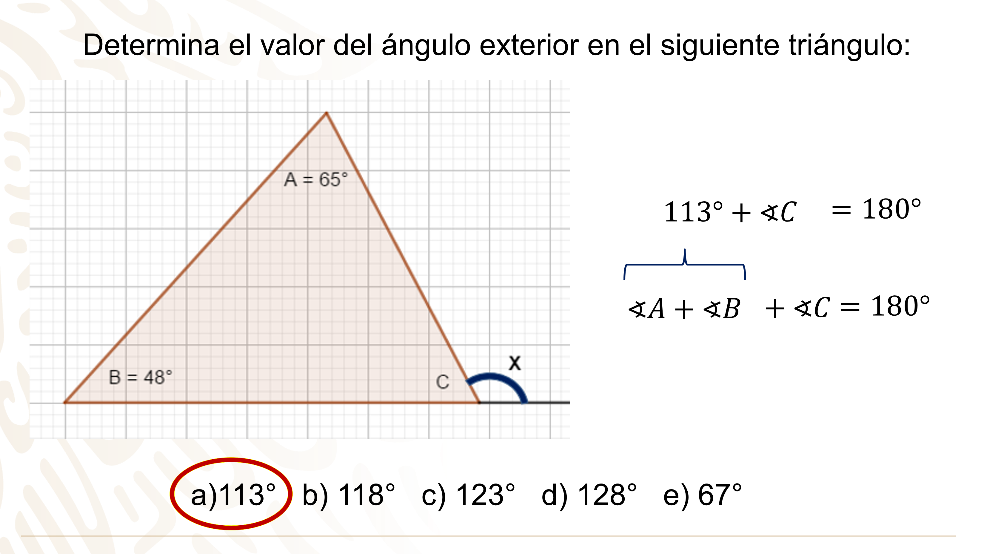
113°, b) 118°, c) 123°, d) 128°, e) 67°
En el triángulo la incógnita es un ángulo externo y los que se conocen son ángulos interiores no adyacentes a él.
Ya que se identificó lo solicitado, para resolver el ejercicio se puede utilizar el teorema que dice:
En todo triángulo, un ángulo exterior es igual a la suma de los ángulos interiores no adyacentes a él, es decir, el ángulo “X” que es el exterior es igual a la suma del ángulo “A” más el ángulo “B”, sustituyendo valores.
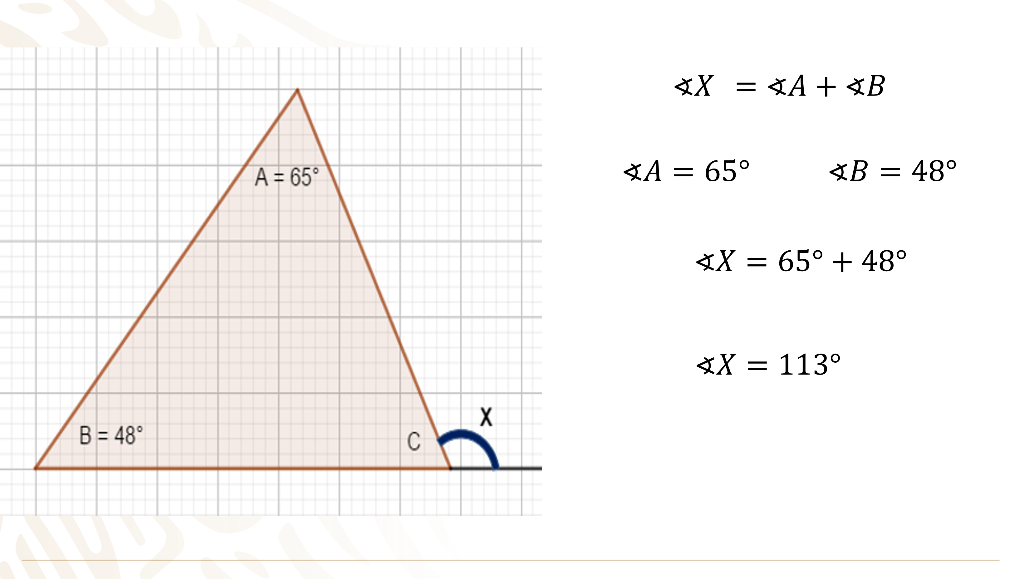
El ángulo “X” es igual a la suma de 48° más 65° que son los interiores no adyacentes a él.
Realizando operaciones tienes que el ángulo “x” es igual a 113°.
La respuesta correcta es el inciso a.
Si se observa la suma de 113° con el ángulo interno faltante “C” se obtiene 180°, ya que son ángulos suplementarios, así como la suma de los ángulos interiores de cualquier triángulo suman 180°, así es posible comprobar que es correcto el teorema utilizado.
Ahora analiza un reto de polígonos.
¿Cuál es el número de diagonales totales que pueden trazarse en un heptágono?
Los resultados posibles son:
- 21, b) 18, c) 14, d) 13, e) 11
Al ser un heptágono se trata de una figura de 7 lados, con este dato puedes emplear la fórmula para calcular el número total de diagonales “D” que tiene una figura.
“D” es igual a “n” menos 3 por “n” entre dos, donde “n” es el número de lados.
Sustituyendo “n” el número de lados que es 7 en la fórmula, tienes que “D” es igual a 7 por 7 menos 3 entre 2, realizando operaciones tienes que 7 por 4 entre 2, es igual a 28 entre 2, el número de diagonales es igual a 14.
La respuesta correcta es el inciso c.
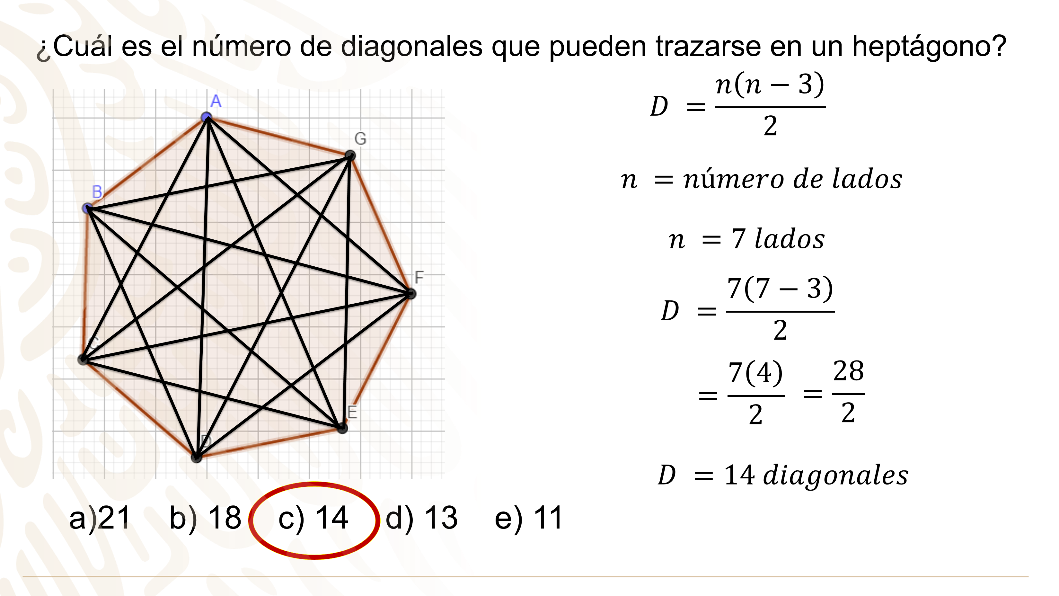
Si trazas las diagonales sobre un heptágono se observa que son 14 sin repetir ninguna diagonal.
Analiza un ejercicio diferente.
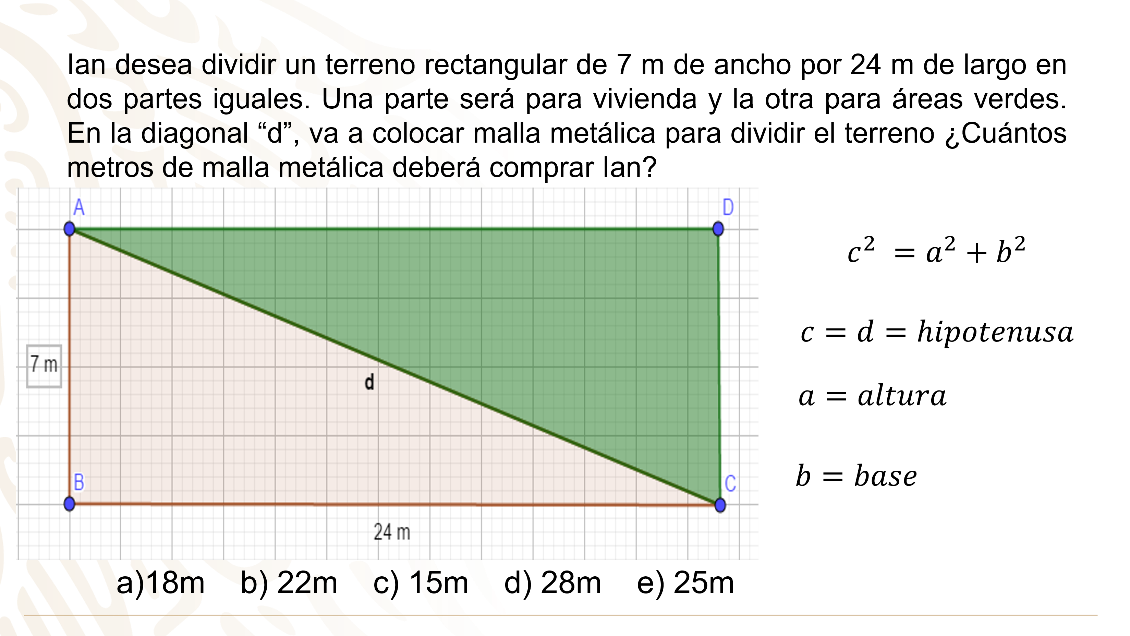
Inicia dibujando la figura que es un rectángulo y le colocas sus datos para identificar lo solicitado y así plantear una estrategia de solución.
Es un rectángulo de base 24 m, altura 7 m y dibujas la diagonal “d” que es donde se colocará la malla y es el valor solicitado.
Con los datos y el valor solicitado, se observa que se forma un triángulo rectángulo, por lo que puedes utilizar como estrategia de solución el teorema de Pitágoras, que dice: que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
En donde la diagonal representa a la hipotenusa.
Los datos proporcionados de altura y base son los catetos a y b del triángulo rectángulo.
Si tienes la fórmula hay que sustituir los datos en ella.
El cuadrado de la diagonal es igual a 7 al cuadrado más 24 al cuadrado, realizando operaciones tienes que 49 más 576 es igual a 625.
Se aplica operación inversa en ambos miembros de la igualdad, para eliminar el cuadrado de la “d”, aplicas la raíz cuadrada y obtienes que la diagonal es igual a 25 m, en este caso son los metros de malla, que es la respuesta correspondiente al inciso e.
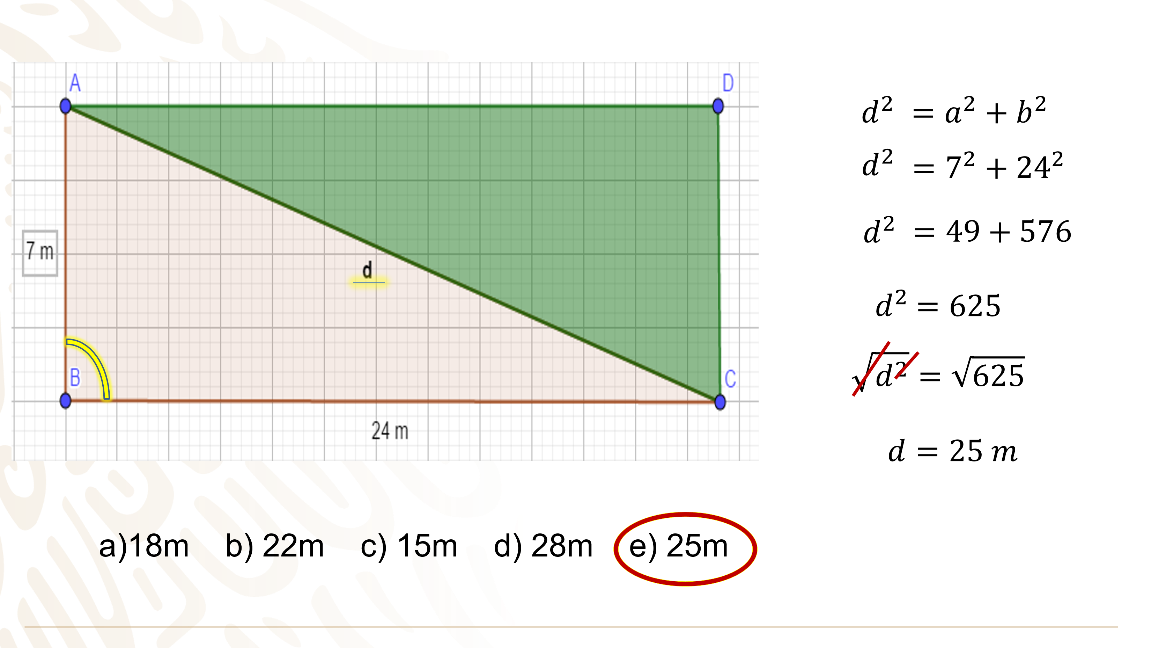
Puedes comprobar que el resultado es correcto, porque en todo triángulo a lado mayor se opone al ángulo mayor, en este caso el lado más grande de 25 metros se encuentra enfrente del ángulo mayor que es el de 90°.
El uso de triángulos rectángulos para la solución de problemas es muy amplio, no solo con el teorema de Pitágoras que relaciona los lados de un triángulo rectángulo.
También es posible relacionar los lados y los ángulos de un triángulo rectángulo a través del uso de razones trigonométricas.
Analiza el siguiente ejercicio:
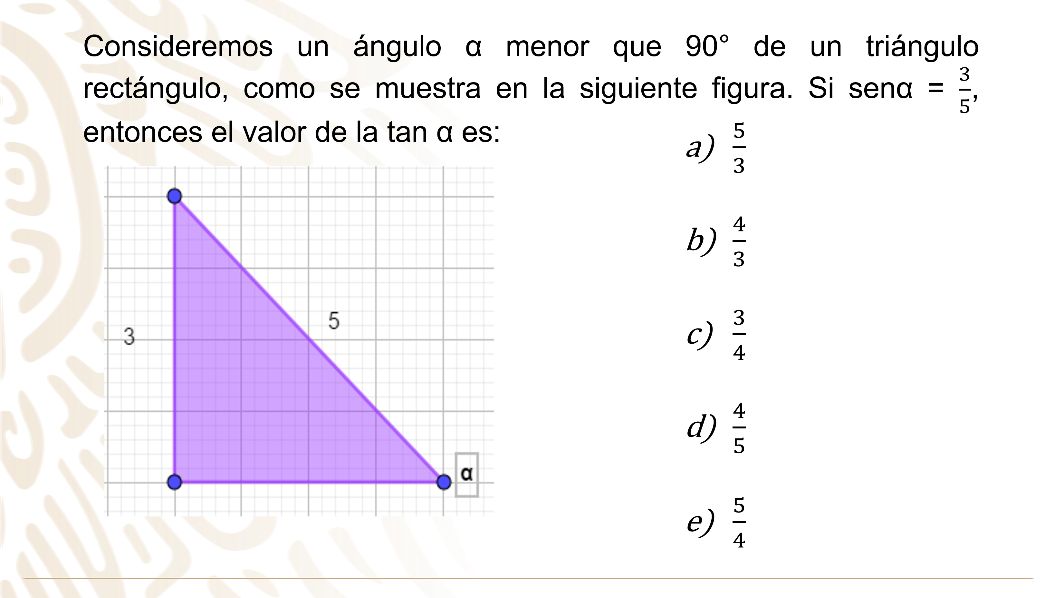
El ejercicio proporciona como dato la razón seno y solicita el valor de la razón tangente, por lo tanto, es importante conocer ambas razones trigonométricas.
Si el seno es igual a cateto opuesto sobre hipotenusa, ya conoces los valores de esos dos lados y la tangente es igual a cateto opuesto sobre cateto adyacente. El valor desconocido es el cateto adyacente, que se debe calcular primero para sustituirlo en la fórmula.
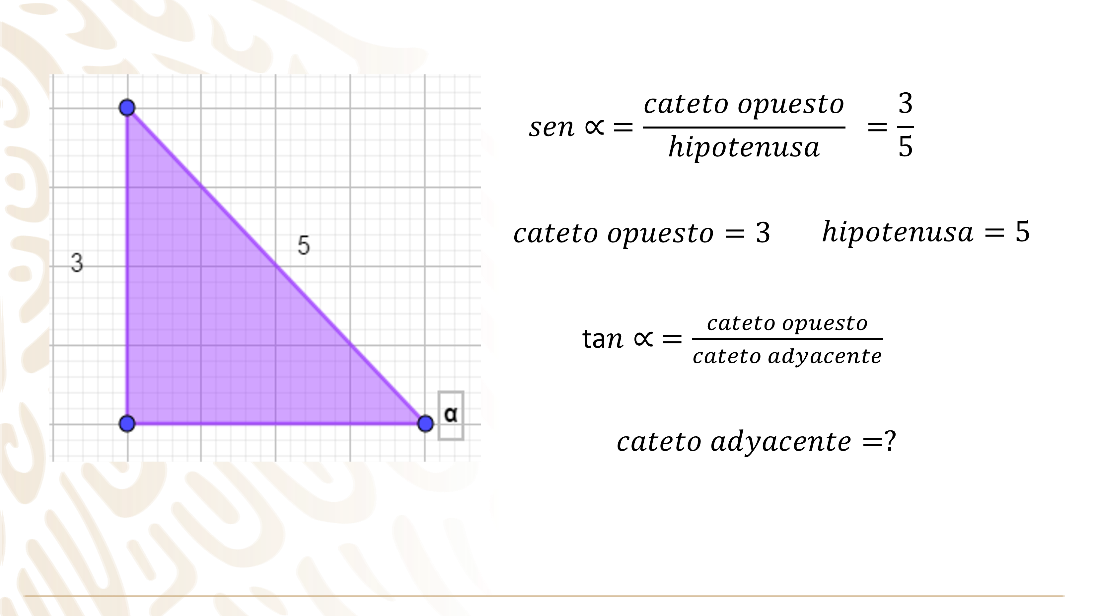
Si te proporcionan como dato los lados del triángulo rectángulo y ningún ángulo a parte del ángulo recto, entonces se puede utilizar el teorema de Pitágoras para calcular el valor faltante y sustituir el valor en la función trigonométrica para encontrar el resultado.
El valor faltante es el cateto adyacente, por lo tanto, es igual a la raíz cuadrada de la diferencia del cuadrado de la hipotenusa menos el cuadrado del cateto opuesto.
Sustituyes valores y tienes que el cateto adyacente es igual a la raíz de 5 al cuadrado menos 3 al cuadrado, realizando operaciones tienes que la raíz de 25 menos 9 es igual a la raíz de 16, igual a 4.
El valor del cateto adyacente es 4, si sustituyes en la fórmula de la tangente, tienes que es cateto opuesto entre cateto adyacente, es igual a 3 entre 4, o tres a cuatro o tres cuartos.
El resultado es el inciso c.
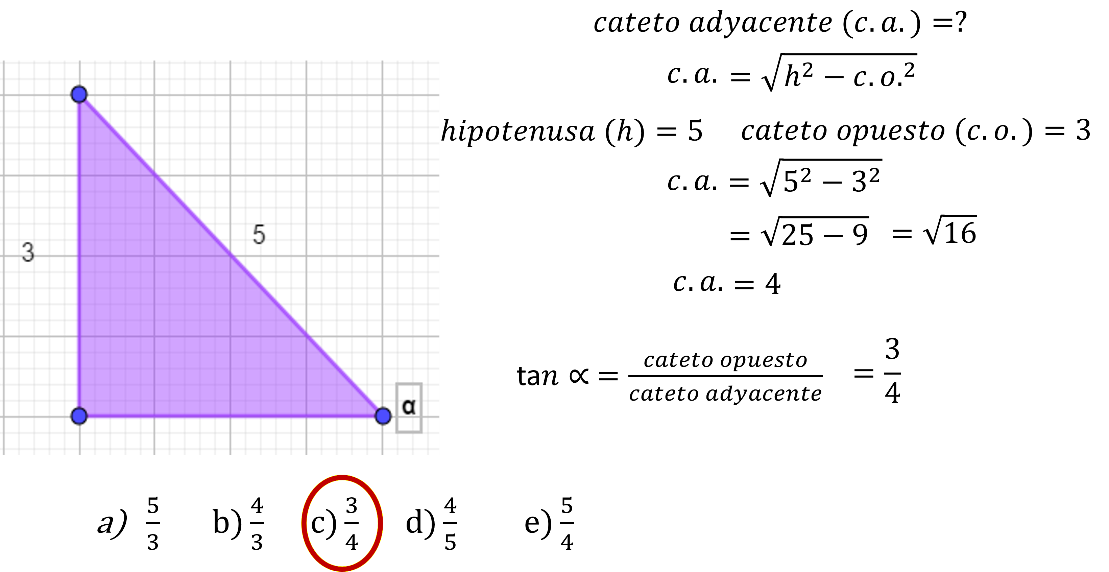
Analizando los resultados se observa que se trata de la terna pitagórica en donde los catetos son 3 y 4 y la hipotenusa es 5. Conociendo estos valores solo se calcula la razón trigonométrica solicitada.
Analizas ahora un ejercicio que relaciones los lados y los ángulos de un triángulo rectángulo:
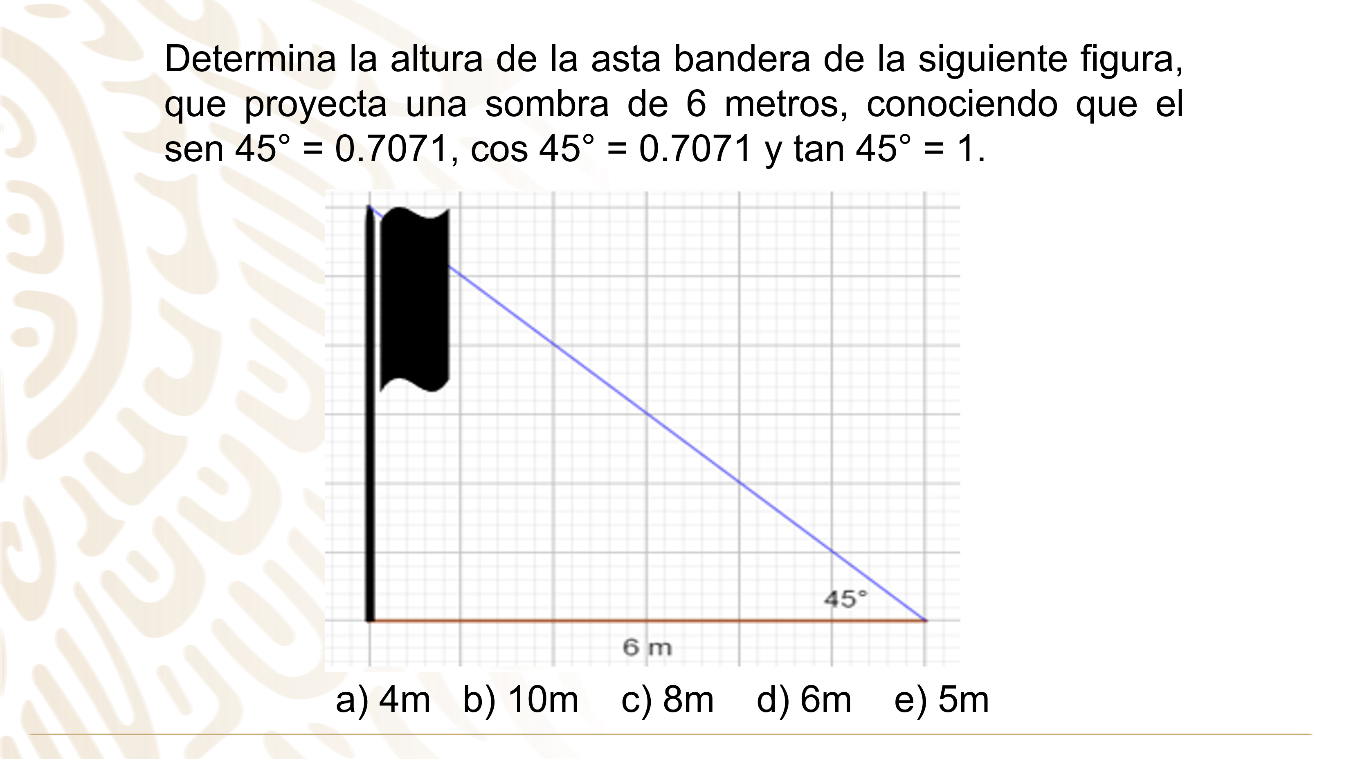
El ejercicio proporciona varios datos, algunos no son necesarios, porque del ángulo menciona el valor de las tres razones trigonométricas de las cuales solo se ocupa una.
Es importante identificar cual es la necesaria y esto depende de los datos proporcionados y el valor solicitado.
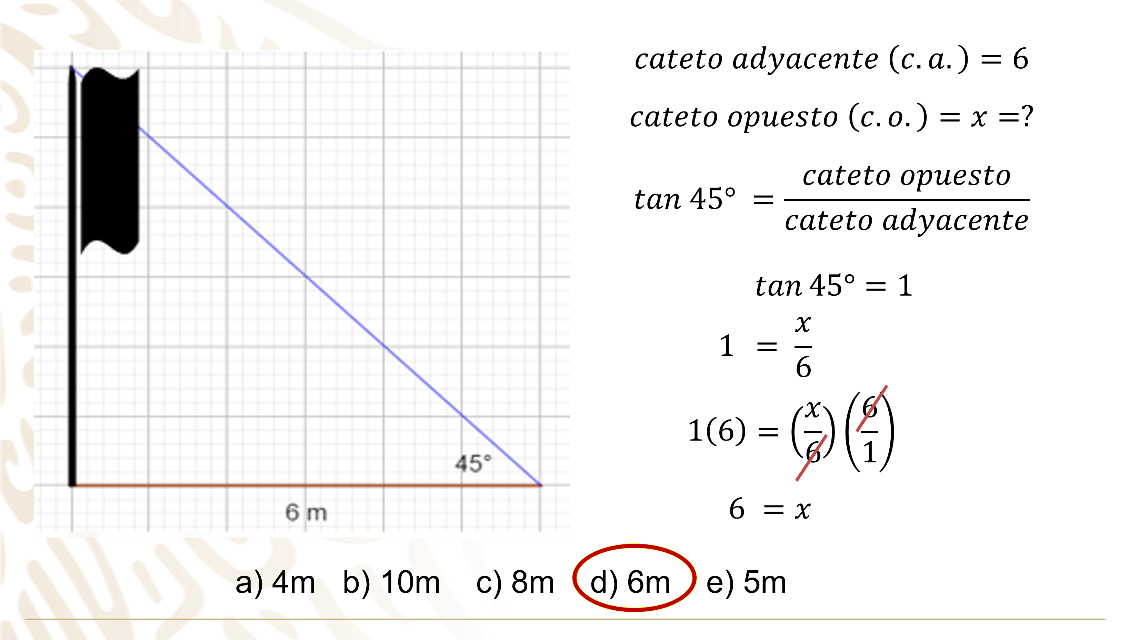
Se observa que de la figura tienes que la sombra de la asta bandera representa el cateto adyacente del ángulo de 45° ya que forma parte del mismo ángulo.
El valor que se solicita calcular es el cateto opuesto, porque, la altura de la asta bandera se localiza enfrente del ángulo de 45°.
Si el seno es cateto opuesto entre hipotenusa, el coseno es cateto adyacente entre hipotenusa y la tangente es cateto opuesto entre cateto adyacente.
Se puede concluir que la razón que se necesita es la tangente, porque es quien tiene el dato y el valor solicitado, entonces se debe de sustituir los valores en la fórmula.
La tangente de 45° es igual a cateto opuesto entre cateto adyacente, sustituyendo los datos tienes que la tangente del ángulo de 45° que es 1, es igual a “x” que es el valor desconocido o cateto opuesto, entre 6 qué es la sombra de la asta bandera o cateto adyacente.
Para despejar a “x” se multiplica por 6 a ambos miembros de la igualdad y tenemos que 6 por 1, es igual a “x” entre 6 por 6, se realizan operaciones “x” es igual 6.
La opción correcta es el inciso d.
Has analizado varios temas a lo largo de la sesión y ya te encuentras listo para poner a prueba los temas analizados.
Toma nota en tu cuaderno de los siguientes ejercicios con 5 opciones de solución de los temas analizados en la sesión, con las estrategias seguidas y la opción correcta para su posterior análisis.
Comparte con tus compañeros y maestros los resultados obtenidos y estrategias de solución, ya que al compartir tus experiencias de conocimiento estas se multiplican.
Primer ejercicio:
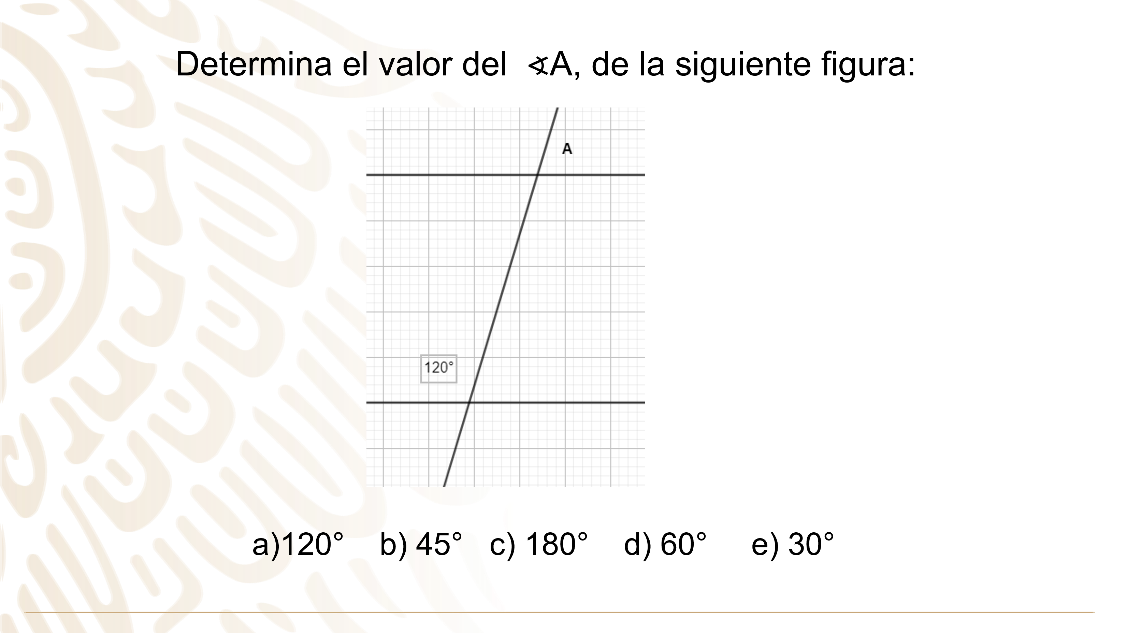
Segundo reto:
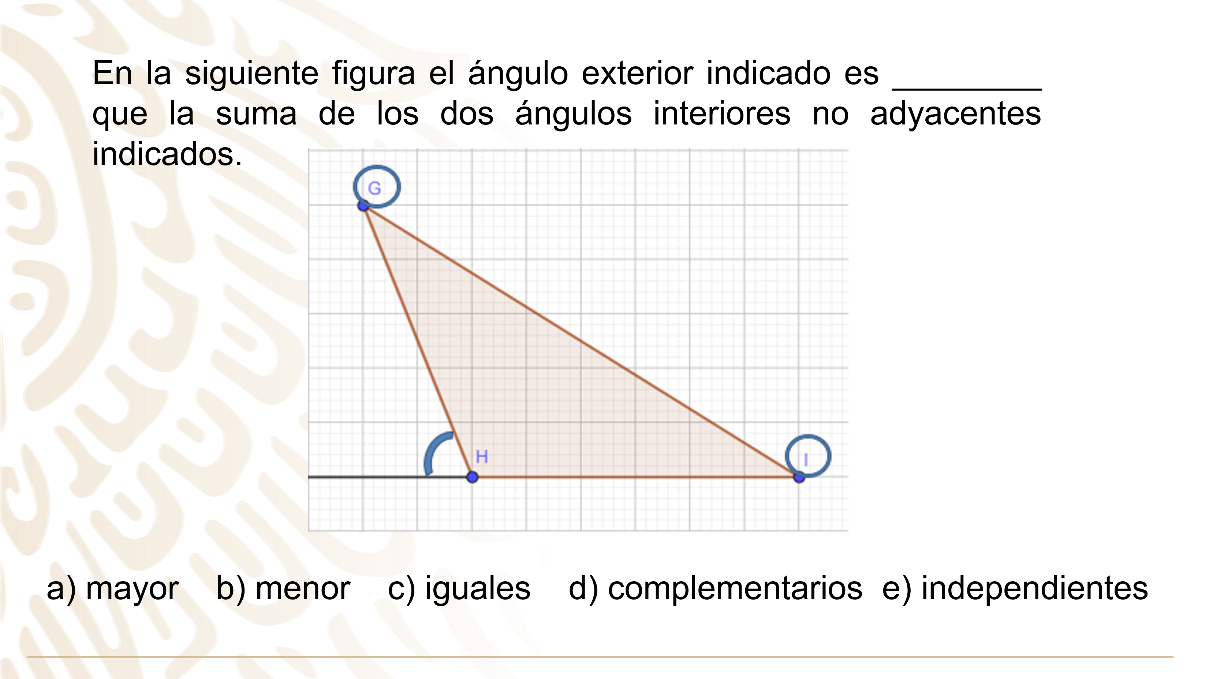
Tercer reto:
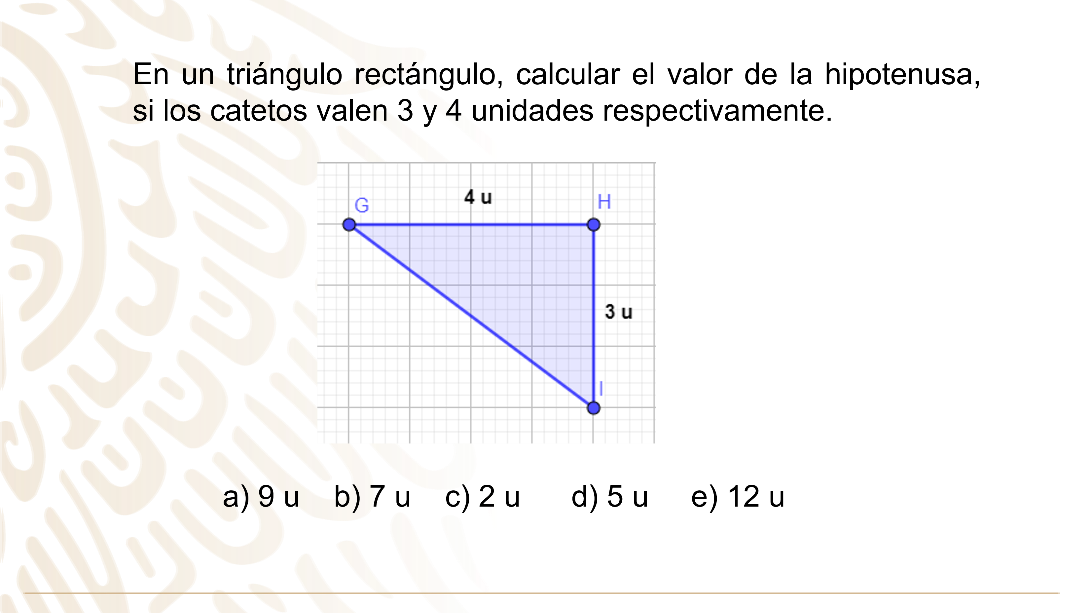
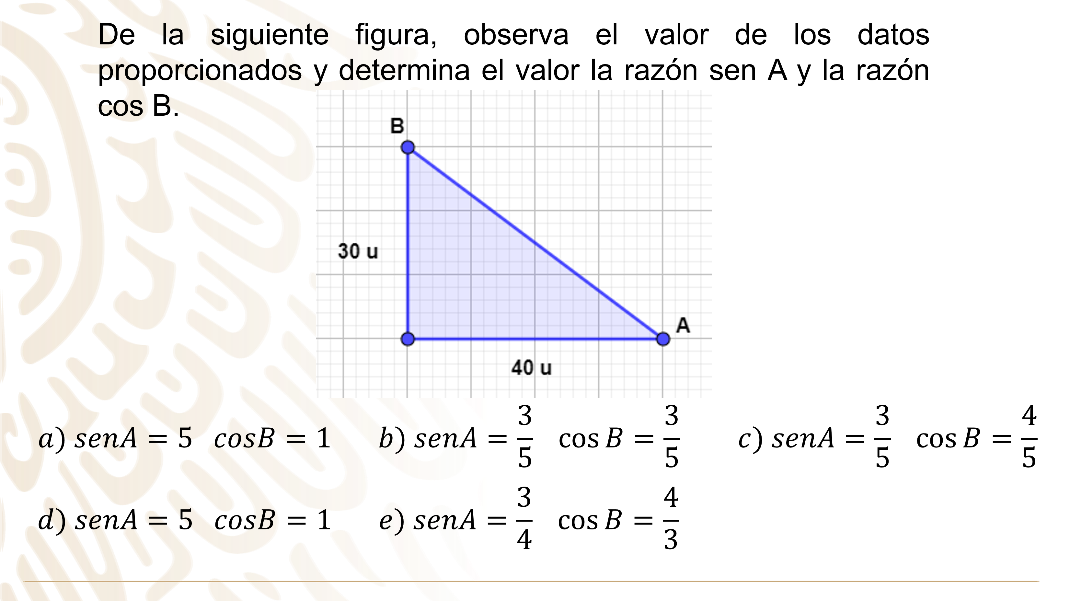
Cuarto y último reto:
En la sesión analizaste varios ejercicios del eje Forma, espacio y medida.
La variedad de temas que se abordaron brinda una muestra de lo extenso y complejo que se pueden presentar los ejercicios, así como la variedad de métodos o estrategias para resolver dichos ejercicios.
Por esa razón es importante tomar nota de los ejercicios, de las dudas que se puedan presentar para investigarlas, así como de seguir practicando retos similares ya que cada reto es único y diferente.
Como decía el matemático George Polya, para resolver un ejercicio, uno aplica un procedimiento que lo lleva a la respuesta.
El reto de hoy:
Para resolver un problema o ejercicio, es necesario hacer una pausa, reflexionar y hasta puedes ejecutar pasos originales que no habías ensayado antes para dar la respuesta. Esta característica de dar una especie de paso creativo es la solución.
Puedes consultar guías de estudio, problemas en libros de texto, simuladores en línea o sitios de internet autorizados para fortalecer lo aprendido.
La práctica te brindará confianza y seguridad para retos futuros.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.