Resolución de problemas geométricos mediante el Teorema de Tales
Resolución de problemas geométricos mediante el Teorema de Tales
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: resolver problemas que impliquen el Teorema de Tales.
¿Qué vamos a aprender?
Trabajarás con la resolución de problemas geométricos mediante el teorema de Tales, utilizarás tu libreta de matemáticas, una regla o escuadra y un lápiz.
¿Qué hacemos?
Uno de los centros arqueológicos más impresionantes del mundo es Teotihuacán. Y sí, están en la clase correcta, porque las matemáticas, y particularmente la geometría, también se pueden aplicar para encontrar la altura de objetos tan grandes como la Pirámide del Sol.
Has observado la gran cantidad de formas geométricas y líneas que hay a tu alrededor, por ejemplo:

cuadrados,

rectángulos,

triángulos,

círculos,

líneas horizontales,

verticales,

paralelas

o perpendiculares.

Estas líneas y formas geométricas simples las utilizaron las mujeres y hombres de la antigüedad para elaborar objetos e instrumentos que les permitieran mejorar su vida diaria, por ejemplo:
lanzas,

flechas, y uno de los elementos circulares y

más importante: la rueda

También pudieron construir magníficas edificaciones como las ya conocidas pirámides. Todo esto contribuyendo notablemente al desarrollo de la geometría la cual, según los registros más antiguos que se conocen, comenzó en Mesopotamia aproximadamente 3,000 años A.C.
Es increíble que aquellos pueblos ya sabían que los lados correspondientes de triángulos rectángulos semejantes son proporcionales.
La geometría también tuvo un importante desarrollo en el antiguo Egipto. Al decaer las civilizaciones egipcia y mesopotámica, gran parte de la geometría desarrollada por estos pueblos pasó a los griegos los cuales la transformaron en una geometría deductiva, en donde las reglas y leyes geométricas se establecen mediante un razonamiento lógico.
Así alrededor del año 600 A.C. el primer individuo a quien se atribuye haber utilizado el método deductivo para demostrar un hecho geométrico fue Tales de Mileto, quien se distinguió por su gran conocimiento

matemático,

astronómico,

filosófico y

geométrico

Lee algunas de sus proposiciones:
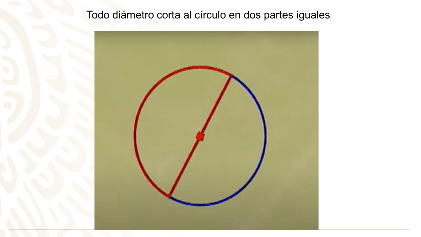
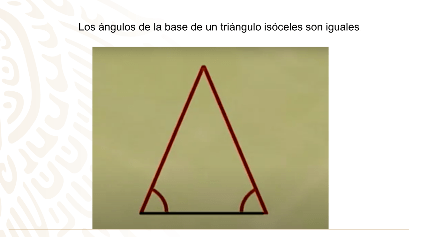
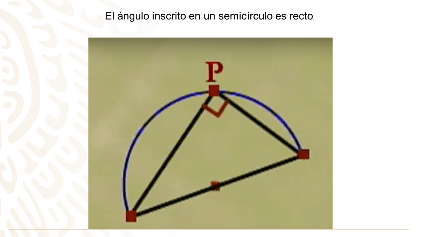
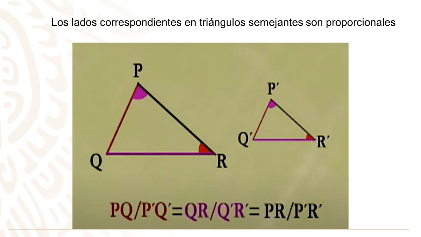
Ahora comprendes porque Tales de Mileto, fue considerado como uno de los siete sabios de la antigüedad.
Antes de revisar el trabajo más conocido del genio de Mileto, el teorema de Tales, primero conoce los diferentes tipos de líneas rectas según la posición entre ellas.
Comienza primero con las líneas rectas paralelas, dos líneas rectas son paralelas si no se cortan en un punto por mucho que las prolongues. Un ejemplo de líneas paralelas serían las vías del tren, las cuales mantienen la misma distancia entre ellas, aunque parezca que se tocan a lo lejos.

Continúa con las Rectas secantes. Dos rectas son secantes si se cortan en algún punto y las dos líneas rectas forman 4 ángulos, pero ninguno de estos ángulos es recto.
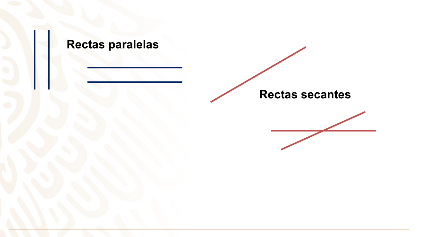
Finalmente, tienes a las líneas rectas perpendiculares las cuales se cortan en un punto formando 4 ángulos rectos, es decir, ángulos de 90º.
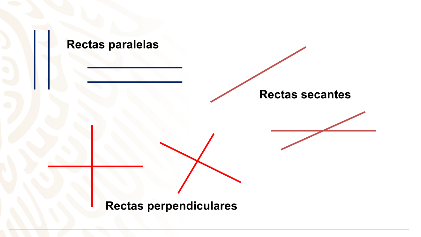
Ahora, sí, con todos estos conocimientos previos, puedes conocer el teorema de Tales.

Recuerda primero lo que significa que dos lados sean correspondientes. Realiza los trazos necesarios para entenderlo.
Aquí tenemos dos rectas que se intersecan,
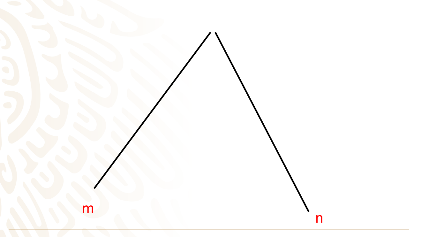
y que son cortadas por estas cuatro paralelas que se han dibujado en color rojo.
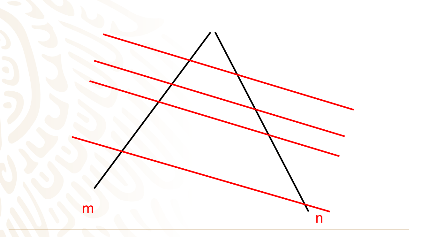
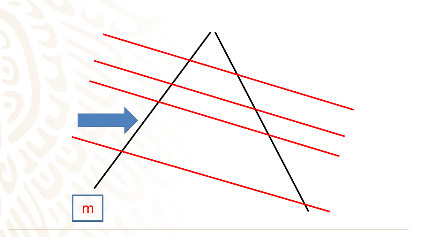
Observa cuales son los segmentos formados por las paralelas en la recta m.
Encontraste a los segmentos AB
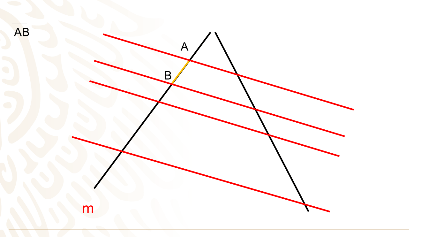
BC
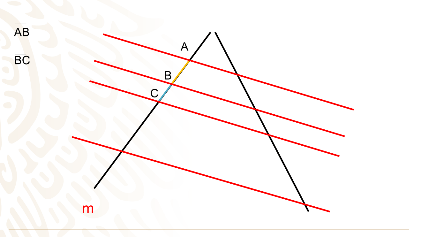
CD y también los segmentos
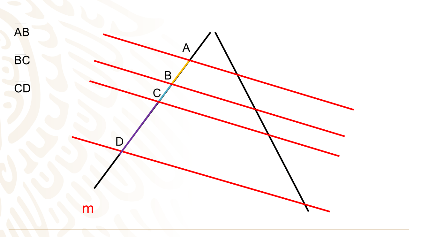
AC
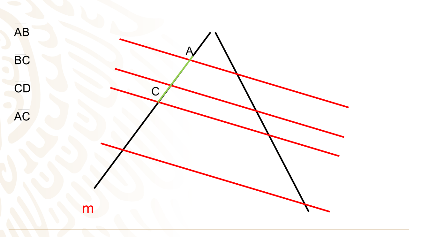
AD y
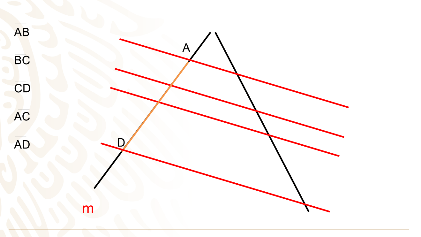
BD
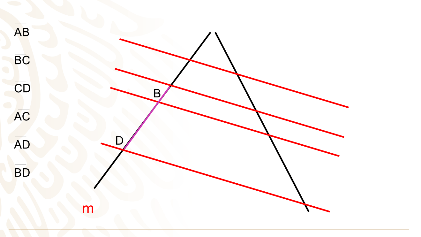
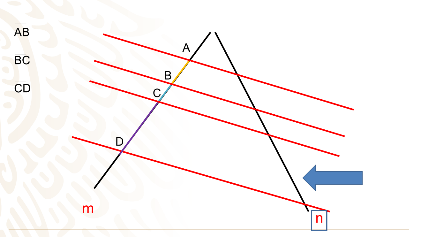
Observa cuales son los segmentos determinados por las paralelas en la otra recta, es decir, en la recta n.
¿Puedes identificar cuáles son los segmentos correspondientes?
Observa cómo cada parte de estos segmentos están formados por las mismas paralelas en las rectas m y n.
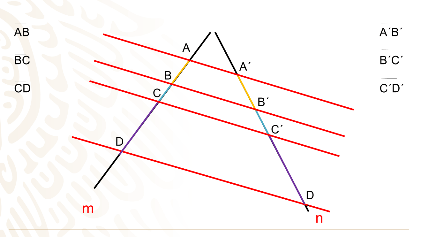
Observa con detenimiento que quiere decir que las medidas de los segmentos correspondientes guarden la misma razón de proporcionalidad.
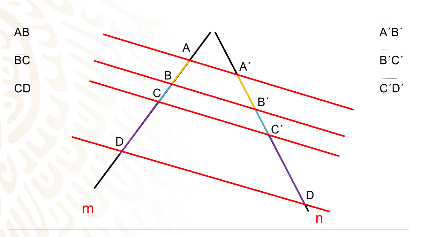
Quiere decir que, si escoges un segmento de la primera recta y divides su longitud por la longitud del segmento correspondiente, obtendrás un número que no depende de los segmentos escogidos.
Escoge el segmento AB su segmento correspondiente es A prima B prima, al medir sus longitudes de estos segmentos, tienes que son
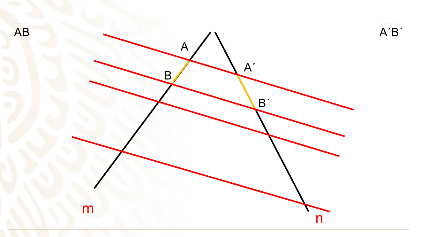
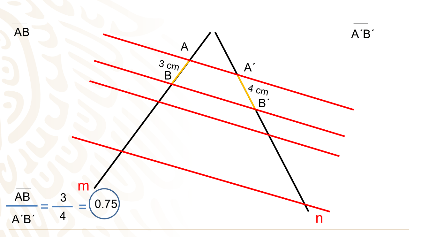
3 y 4 cm respectivamente.
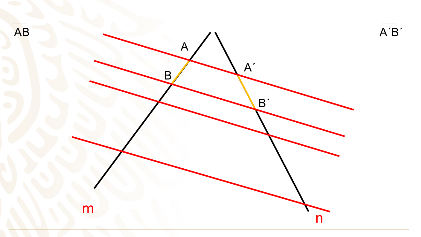
La razón o cociente de sus longitudes es igual a 0.75
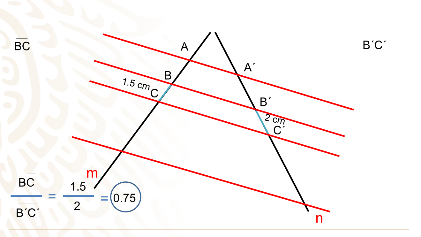
Escoge ahora otro par de segmentos correspondientes por ejemplo los segmentos BC y B prima C prima cuyas longitudes fueran de 1.5 cm y 2 cm respectivamente,
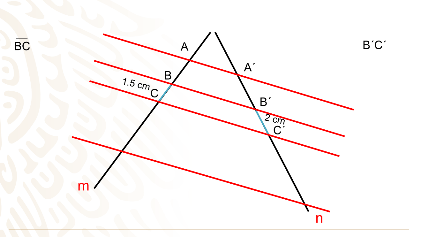
al realizar el cociente obtendrías que es exactamente de 0.75.
Escoge un último par de segmentos correspondientes CD y C prima D prima con longitudes de 6 y 8 cm respectivamente, haz su cociente y
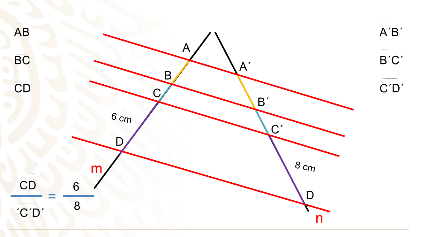
De nuevo obtienes 0.75.
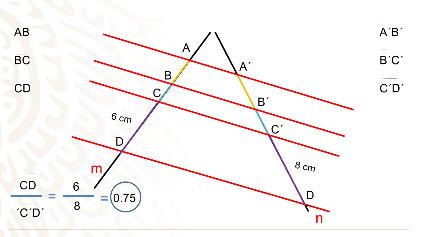
Es decir, esta condición se va a cumplir para cualquier par de segmentos correspondientes. Este es el teorema de Tales.
Observa ahora un ejemplo de la aplicación de este extraordinario teorema a través de una anécdota atribuida al mismísimo genio de la Geometría: Tales de Mileto.
Se dice, que Tales andaba en busca de un método que permitiera medir la altura de objetos que por tener difícil acceso era imposible lograrlo.
En su recorrido por el Mediterráneo, se encontró con un faraón de Egipto. Cierta mañana cuando pasaban cerca de la Gran pirámide de Keops, el faraón, sabiendo que Tales era famoso por su gran ingenio y su conocimiento en matemáticas, le propuso que calculara la altura de ese majestuoso monumento, es decir la altura de la Pirámide.
¿Cómo medir la altura de una pirámide?
Tales utilizó su teorema para calcular la altura de la pirámide de Keops.
¿Cómo crees que Tales lo logró?
He aquí la respuesta:
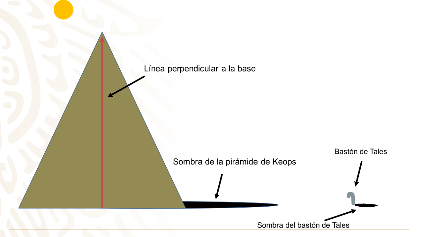
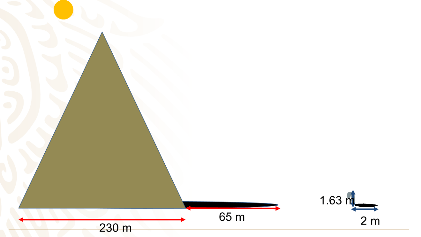
Como, Tales no podía medir directamente la perpendicular a la base de la pirámide, lo primero que hizo fue medir uno de sus lados. Previamente Tales había medido la longitud de su bastón.
Luego a la misma hora de un día soleado midió la longitud de la sombra de la pirámide y la longitud de la sombra de su bastón, el cual había colocado de forma vertical sobre la arena. Así obtuvo los siguientes datos:
La altura del bastón: 1.63m
La longitud de la sombra del bastón: 2m
Longitud de la base de la pirámide: 230
Longitud de la sombra de la pirámide: 65 m
A partir de estas medidas, Tales pudo calcular que: como la base de la pirámide medía 230 m, su mitad era de 115m, y sumando la longitud de la sombra que fue de 65m, obtuvo que la distancia desde la base de la altura hasta la punta de la sombra era de 180 m. Designa con la letra a, a la altura de la Pirámide que Tales quería obtener
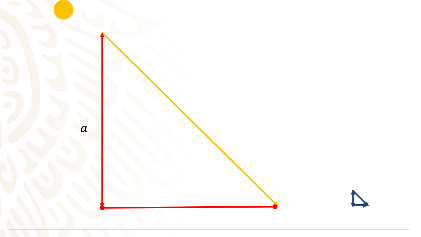
Elimina las figuras de la pirámide y del bastón y deja solamente los triángulos que los representan.
Observa que tienes todos los elementos necesarios para utilizar el Teorema de Tales, tal y como él los utilizó.
Dos rectas que se intersecan, que son las rectas a, es decir la altura, y la recta que pasa por las bases de la pirámide y de la longitud de la sombra del bastón de Tales.,
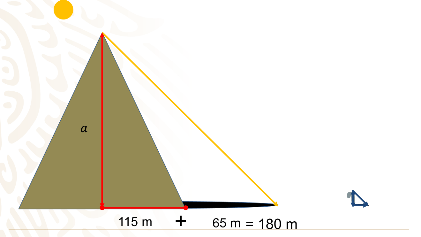
También puedes ver las rectas paralelas, que en este caso son los rayos del Sol los cuales se proyectan sobre la Tierra formando las sombras.
Ahora aplica el Teorema de Tales:
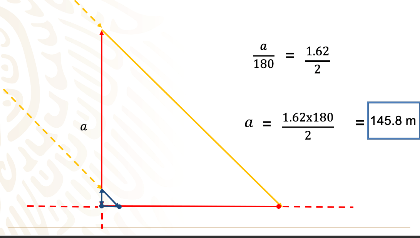
La altura a de la pirámide dividida entre la longitud de su sombra que es de 180 m, es igual a la longitud del bastón que es 1.62m entre la longitud de su propia sombra, que en este caso es de 2 m.
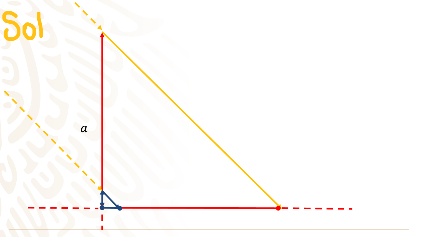
Despeja a la “a”
Obtienes como Tales, que la altura de la pirámide de Keops es de 145.8 metros!
Tales de Mileto se ha ganado un lugar muy importante en la historia de las matemáticas.
Ahora puedes comprender que la semejanza de triángulos es una herramienta muy poderosa para garantizar ya sea el paralelismo de segmentos o bien la proporcionalidad de segmentos.
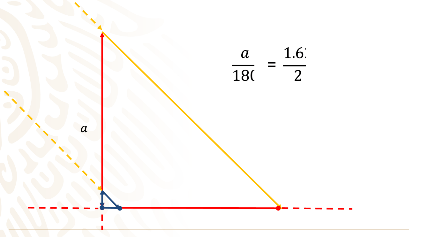
Repasa una vez más el Teorema de Tales y conoce lo que es el inverso de este importante teorema.
A continuación, utilizarás el Teorema de Tales para justificar algunos resultados matemáticos.
Escribe posibles respuestas a la pregunta anterior. El cuadrilátero PQRS es:
¿Pensaste en alguna de estas respuestas? ¿Tienes más opciones?
El movimiento de los vértices del cuadrilátero ABCD permite ver que los lados del cuadrilátero PQRS no son del mismo tamaño
- Tales
Tienes que verificar que el cuadrilátero cumple con la característica de los paralelogramos.
2. Tales 2
Comprueba tu aprendizaje resolviendo el siguiente ejercicio:
3. Tales 3
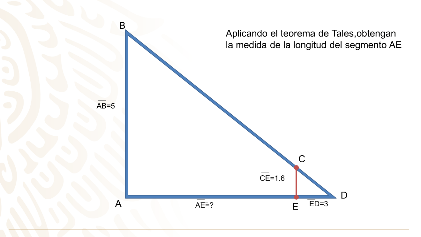
Aplicando el teorema de Tales, obtén la medida de la longitud del segmento AE.
4. Tales 4
5. Tales 5
6. Tales 6
El reto de hoy:
Recuerda el teorema de Tales:

¡Buen trabajo!
Gracias por tu esfuerzo.