Resolución de problemas

Resolución de problemas

Aprendizaje esperado: resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro, kilogramo y de unidades del Sistema Inglés (yarda, pulgada, galón, onza y libra).

Énfasis: dar sentido y significado a la resolución de problemas que implican conversión de unidades de longitud.

¿Qué vamos a aprender?

En esta sesión analizarás diferentes situaciones a través de problemáticas que se resuelven mediante conversión de unidades de longitud, entre unidades del Sistema Internacional de Unidades y del Sistema Inglés.

Ten a la mano tu cuaderno, lápiz o bolígrafo, goma y sacapuntas. Así como tu libro de texto. Para que tomes tus notas y escribas las inquietudes que vayan surgiendo.

¿Qué hacemos?

Para iniciar esta sesión reflexiona la siguiente pregunta: ¿Cuáles son las unidades de longitud?

En el Sistema Internacional de Unidades, la principal unidad de medida de longitud es el metro, con sus múltiplos y submúltiplos.

En los submúltiplos se usan los prefijos deci, centi o mili. Estos submúltiplos del metro son:

• Decímetro, es la décima parte del metro, su abreviatura es “dm”, su valor es un décimo de metro y puede nombrarse su equivalencia como cero punto, un metros.
• Centímetro, es la centésima parte del metro, su abreviatura es “cm”, su valor es un centésimo de metro y puede nombrarse su equivalencia como cero punto, cero, un metros.
• Milímetro, es la milésima parte del metro, su abreviatura es “mm”, su valor es un milésimo de metro y puede nombrarse su equivalencia como cero punto, cero, cero un metros.

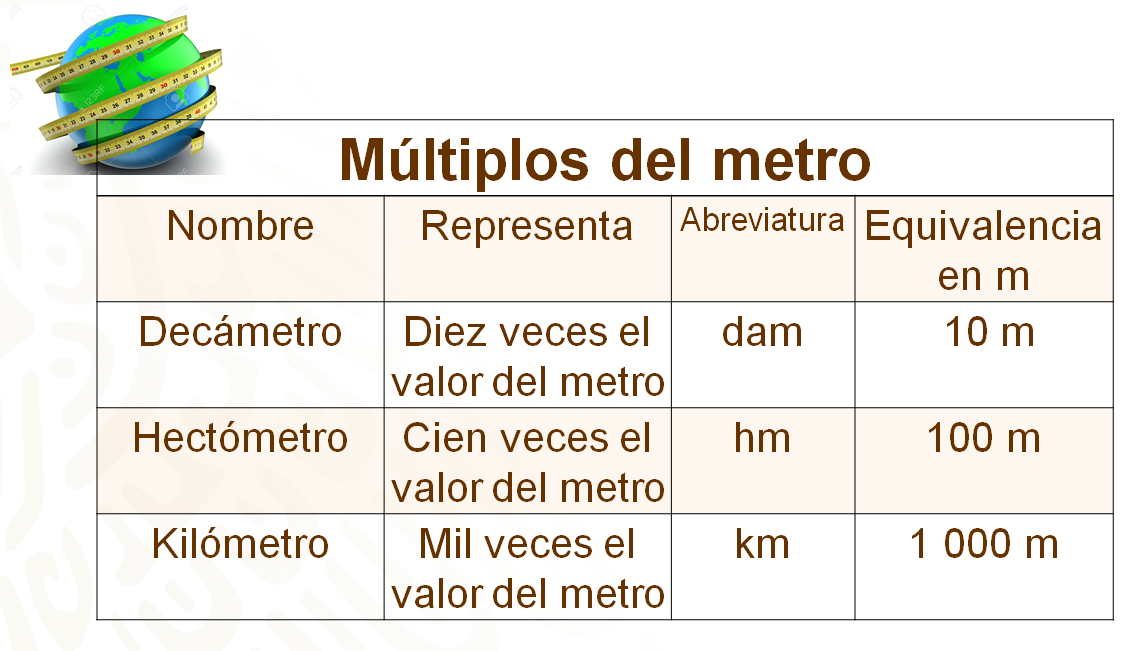
Para nombrar los múltiplos del metro se usan los prefijos deca, hecto, kilo, que refieren a:

• Decámetro que es diez veces el valor del metro, su abreviatura es “dam” y equivale a 10 metros.
• Hectómetro que es cien veces el valor del metro, su abreviatura es “hm” y equivale a 100 metros.
• Kilómetro que es mil veces el valor del metro, su abreviatura es “km” y equivale a 1 000 metros.

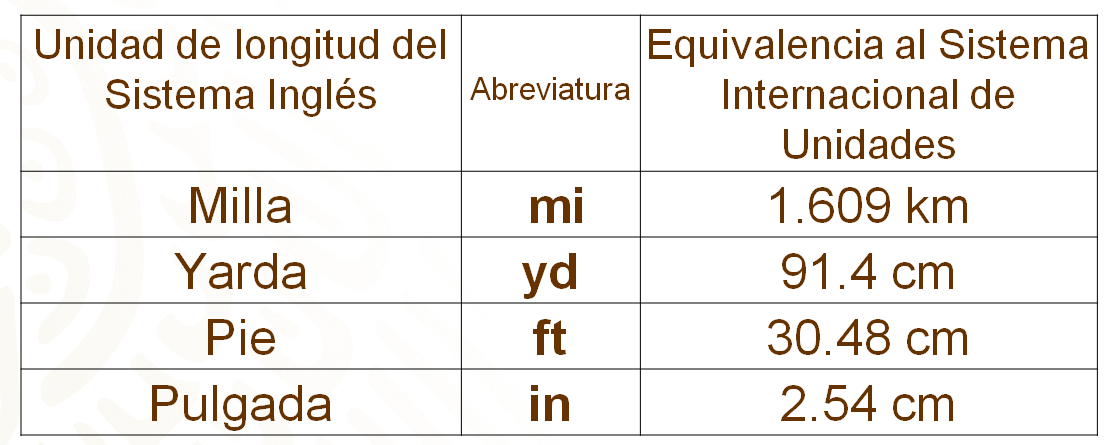
En el Sistema Inglés se usan como medidas de longitud la milla, la yarda, el pie y la pulgada.

Una milla, cuya abreviatura es “mi” equivale a 1 punto 609 kilómetros; una yarda, su abreviatura es “yd” y equivale a 91 punto 4 centímetros; un pie, su abreviatura es “ft” y equivale a 30 punto 48 centímetros y, por último, una pulgada, cuya abreviatura es “in” y equivale a 2 punto 54 centímetros.

A continuación, revisarás algunas situaciones problema en donde se hace uso de la conversión de medidas de longitud.

Marlene es aficionada al basquetbol. Ella investiga acerca de uno de los mejores jugadores de todos los tiempos en este deporte, Michael Jordán; al leer sobre tal personaje encuentra que tiene una estatura de 6 ft 6 in, pero no tiene idea a qué se refiere esta información, ni a cuánto equivale. Así que investiga:

1. ¿A qué unidades de medida se refiere la información que encontró Marlene?
2. ¿Cuál es la estatura de Michael Jordán, en centímetros?
3. ¿Cuál es la estatura Michael Jordán, en metros?

Tú, ¿ya sabes a qué unidades de medida se refiere la información, sobre la estatura de Michael Jordán, que encontró Marlene?

Una manera de contestar esta pregunta es retomar la información de las tablas anteriores e identificar que la abreviatura “ft” en el Sistema Inglés se refiere a pies y que un pie equivale a 30 punto 48 centímetros. Asimismo, en el mismo sistema la abreviatura “in” representa pulgadas y una pulgada equivale a 2 punto 54 centímetros.

Con esto se da respuesta al primer cuestionamiento, que se refiere a medidas de longitud del Sistema Inglés, los pies y las pulgadas.

Una manera de contestar al segundo cuestionamiento es ordenar los datos en un registro tabular con dos columnas. En la primera columna se colocan las medidas en pies; mientras que, en la segunda columna, la medida en centímetros.

Así, se escribe que un pie equivale a 30 punto 48 centímetros, y el dato conocido de 6 pies, lo anotas en la siguiente fila de la primera columna. Como quieres saber la equivalencia de 6 pies en centímetros, colocas una incógnita en la celda correspondiente, en este caso se usará “z”.

Una manera de calcular el valor de “z” es a través de una regla de tres en donde: 1 es a 30 punto 48, como 6 es a “z”.

De aquí se desprende que “z” es igual a 6 pies por 30 punto 48 centímetros, entre un pie; nota que puedes simplificar la medida “pie”, que se encuentra en el numerador y en el denominador.

Al efectuar esta operación se obtiene “z” igual a 182 punto 88 centímetros dividido entre uno. Entonces, “z” es igual a 182 punto 88 centímetros.

Ahora, puedes formar la relación entre pulgadas y centímetros, también en un registro tabular, estableciendo que, una pulgada equivale a 2 punto 54 centímetros, y 6 pulgadas equivalen a “x” centímetros, ya que éste último es el dato que se desea calcular. De aquí se puede establecer la regla de tres.

De esta regla se puede establecer que “x” es igual a 6 pulgadas por 2 punto 54 centímetros, entre una pulgada. Hay que simplificar las “pulgadas” que se encuentran en el numerador y el denominador, por lo que la unidad de medida será en “centímetros”.

Resolviendo, se obtiene que “x” es igual a 15 punto 24 centímetros entre 1, de lo que se concluye que “x” es igual a 15 punto 24 centímetros.

Ahora, para encontrar la equivalencia de la estatura en centímetros se suma la equivalencia de pies a centímetros, en donde se obtuvo 182 punto 88 centímetros; con la equivalencia de pulgadas a centímetros de la cual se obtuvo 15 punto 24 cm.

Entonces, se establece la suma: 182 punto 88 centímetros más 15 punto 24 centímetros. De esta suma se obtiene 198 punto 12. Con esto se da respuesta al segundo cuestionamiento. Así que la estatura de Michael Jordán, en centímetros, es de 198 punto 12.

Ahora solamente te falta saber la equivalencia en metros.

¿Qué piensas que se hace para encontrar esta equivalencia? ¿Ya tienes el resultado?

Puedes establecer otro registro donde se ordenen los datos y te permita visualizar que: 1 metro equivale a 100 centímetros, y “y” metros equivalen a 198 punto 12 centímetros. Siendo “y” la medida, en metros, de la estatura de Michael Jordán.

A partir de la regla de tres se obtiene que “y” es igual a 198 punto 12 centímetros, por 1 metro, entre 100 centímetros. Nota que puedes simplificar a “centímetros” el numerador y “centímetros” del denominador.

Así, tienes que “y” es igual a 198 punto 12 metros, entre 100. Al calcular el cociente se determina que “y” es igual a 1 punto 9 812 metros.

Como se ha estado hablando de estatura, se trunca el resultado en centésimos, que representan los centímetros; entonces, se da respuesta al último cuestionamiento y se concluye que la estatura de Michael Jordán es de 1 punto 9812 metros.

¿Cómo vas hasta aquí? ¿Conoces otra forma de convertir una medida dada en centímetros a su equivalente en metros?

También puedes resolver multiplicando de manera directa. Revisa esta opción.

Al inicio revisaste una tabla de equivalencias de los submúltiplos del metro, en ella identificaste que un centímetro es la centésima parte del metro, es decir, un centímetro es igual a cero puntos cero, un metro

Ahora, ya puedes establecer la relación: un centímetro equivale a cero puntos cero, un metro, como 198 punto 12 centímetros equivalen a “x” metros.

De la relación anterior se puede decir que “x” es igual a 198 punto 12 centímetros por cero puntos cero, un metro entre un centímetro.

Para simplificar los centímetros, resuelves la multiplicación de 198 punto 12 por cero puntos cero, un metro, entre 1, obteniendo 1 punto 9812 metros.

Como observas, se obtiene el mismo resultado que con el procedimiento anterior. Ahora tienes dos opciones de conversión, aplica la que más se te facilite.

Revisa otra situación en donde se requiere de conversiones.

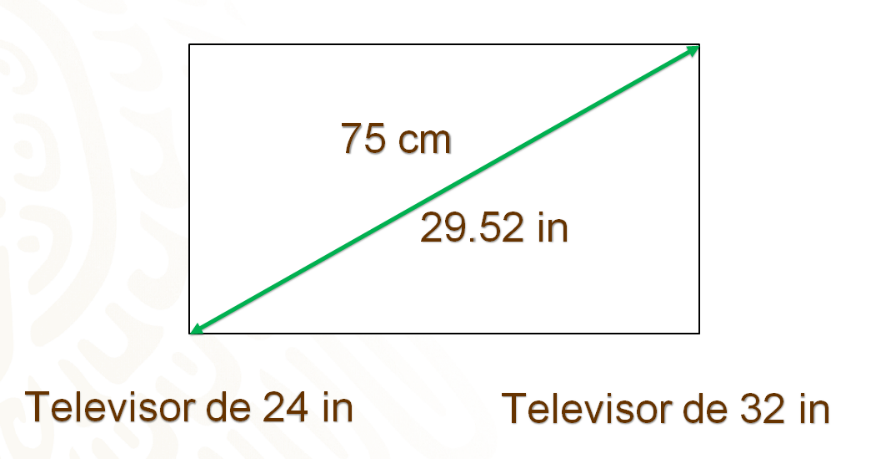
Luisa quiere comprar un televisor. Como ella sabe que la medida que se indica en la presentación de esos aparatos corresponde a la longitud de la diagonal de la pantalla, mide esa dimensión del espacio rectangular del mueble donde piensa colocarla. Encuentra que esta medida es de 75 centímetros.

En la tienda encuentra dos televisores que le gustan. La medida de uno de ellos es de 24 pulgadas y del otro, 32 pulgadas. ¿Qué televisor puede caber en el espacio del que dispone?

Sin hacer cálculos escritos, anota cuál televisor piensas que puede caber en el espacio del que dispone Luisa. ¿Será solamente uno de ellos? ¿Podrán ser ambos? ¿Qué puedes hacer para resolver este problema?

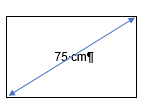
Una manera de contestar el problema es determinar a cuántas pulgadas equivalen los 75 centímetros, para luego, comparar esta equivalencia con la medida de cada televisor que le gustó.

Se puede hacer un registro tabular en donde se establezca la relación entre los centímetros y las pulgadas; sabes que 2 punto 54 centímetros equivalen a una pulgada, entonces, debes calcular a cuántas pulgadas equivalen 75 centímetros. A este valor desconocido se le representará con una incógnita, “y” en este caso.

Se puede calcular el valor desconocido a través de una regla de tres, de donde se obtiene que “y” es igual 75 centímetros por 1 pulgada, entre 2 punto 54 centímetros. Simplificas los centímetros. Así, se tiene que “y” es igual al cociente de 75 pulgadas entre 2 punto 54. Entonces, “y” es aproximadamente igual a 29.52 pulgadas.

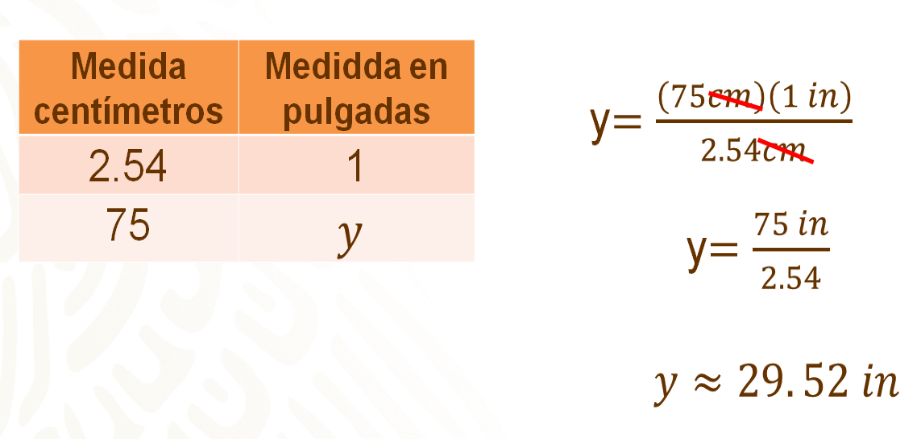
Ahora ya sabes que el espacio disponible es de aproximadamente 29 punto 52 pulgadas.

Entonces, se puede afirmar que, de los televisores que le gustaron a Luisa, solamente puede caber en el espacio del que dispone para colocarlo el de 24 pulgadas, ya que el de 32 pulgadas excede el espacio disponible.

¿Esta respuesta coincide con lo que pensaste antes de resolverlo?

Como te pudiste dar cuenta, las conversiones entre unidades de longitud son necesarias y muy frecuentes en situaciones cotidianas.

Revisa otra situación problema.

María se está preparando para una carrera de larga distancia, por lo que, en su entrenamiento diario debe correr 12 kilómetros. Si está entrenando en una pista de atletismo de 800 metros:

1. ¿Cuántas vueltas debe dar a la pista para completar su entrenamiento diario?
2. Si en un día ha dado 9 vueltas, ¿cuántos metros le faltan para terminar su entrenamiento de ese día?

¿Qué piensas que se puede hacer para resolver el problema?

Anota tu estrategia y tus resultados en tu cuaderno. Luego, compáralos con lo que aquí se te presenta, para ratificar o rectificar lo que hiciste.

Una manera de iniciar la resolución del problema es calcular el número de metros que debe recorrer en su entrenamiento diario. Para ello, puedes organizar los datos en un registro tabular, donde se establece que un kilómetro equivale a 1 000 metros, entonces 12 kilómetros serán un número “x” de metros, donde “x” es el valor desconocido.

Aplica la regla de tres, y obtienes que “x” es igual a 12 kilómetros por 1 000 metros, entre un kilómetro. Aquí se simplifica la unidad de medida “kilómetros”.

Entonces, se tiene que “x” es igual a 12 000 metros entre 1. El cociente obtenido es 12 000 metros, que es la cantidad de metros que María debe recorrer en su entrenamiento diario.

Ahora, ya puedes continuar calculando cuántas vueltas debe dar a la pista, ya que tienes ambos datos en metros.

¿Ya sabes qué operación necesitas realizar?

Se puede realizar una división. Realízala.

Una manera de contestar la primera pregunta es organizando los datos en una tabla, en donde puedes establecer que una vuelta corresponde a 800 metros, y “x” vueltas corresponden a 12 000 metros.

Aplicas la regla de tres, y obtienes que “x” es igual a una vuelta por 12 000 metros, entre 800 metros. Aquí se simplifican los “metros”.

Entonces, se tiene que “x” es igual a 12 000 vueltas entre 800.

El cociente obtenido es 15 vueltas, por lo que se puede afirmar que, para que María pueda completar su entrenamiento diario necesita dar 15 vueltas a la pista de atletismo.

Continua con el siguiente cuestionamiento: Si en un día ha dado 9 vueltas, ¿cuántos metros le faltan para terminar su entrenamiento de ese día?

De los datos de la tabla se puede establecer que, en una vuelta a la pista se recorre 800 metros, por lo que se debe calcular el valor de “x” que son los metros que recorre al dar 9 vueltas.

Aplicando la regla de tres se obtiene que “x” es igual a 9 vueltas por 800 metros, entre una vuelta. Simplifica la unidad de medida “vueltas”.

De manera que “x” es igual a 7 200 metros entre 1. Por lo que sabes que, al dar 9 vueltas a la pista, María recorre 7 200 metros. Si en su entrenamiento diario debe recorrer 12 000 metros y un día ha recorrido 7,200 metros; Entonces, realizas una resta para saber cuántos metros le faltan por recorrer.

¿Cómo vas? ¿Ya tienes el resultado en casa?

La respuesta es que le faltan por recorrer 4 800 metros.

Así, se ha dado solución a este problema.

Ahora, regresa a lo que anotaste al inicio de este problema.

¿Tu estrategia fue igual a la utilizada aquí? ¿tus resultados coinciden con los que aquí se obtuvieron?

Revisa tus estrategias y resultados, en caso necesario y posteriormente, analiza dónde debes trabajar para superar las dificultades que encontraste.

Revisa la siguiente situación.

Un amigo de María que vive en Estados Unidos se está preparando para un maratón y le platica a María que él recorre 8 millas en su entrenamiento diario.

1. ¿Quién recorre una distancia mayor en su entrenamiento diario, María o su amigo?

Sin hacer cuentas escritas, contesta la pregunta y registra tu respuesta en tu cuaderno.

Ahora, ¿qué piensas que puedes hacer para resolver este problema?

Una manera de iniciar es recordar que María recorre 12 kilómetros diariamente. Entonces, puedes retomar que la equivalencia de una milla es igual a 1 punto 609 kilómetros.

1 mi = 1.609 km

Después, puedes calcular cuántos kilómetros recorre el amigo de María en su entrenamiento diario.

Ordenas los datos en una tabla que te permite establecer que una milla equivale a 1 punto 609 kilómetros, y que 8 millas equivalen a “x” kilómetros.

Haciendo uso de la regla de tres tienes que “x” es igual a 8 millas por 1 punto 609 kilómetros, entre una milla. Simplificas la unidad de medida “millas” y al calcular el producto se obtiene 12 punto 872 kilómetros, entre 1.

De ahí, se tiene que “x” es igual a 12 punto 872 kilómetros.

Con dicha información ya puedes determinar que el amigo de María recorre una distancia mayor en cada entrenamiento diario, ya que él recorre 12 punto 872 kilómetros y María, 12 kilómetros.

Continuando con los deportes.

Se sabe que el campo de futbol americano, incluyendo la zona final, mide 120 yardas de largo y 53.3 yardas de ancho. El entrenador pide a sus jugadores que, para el calentamiento, den dos vueltas alrededor del campo de juego.

¿Cuántos metros recorren los jugadores para su calentamiento?

Largo: 120 yd.

Ancho: 53.3 yd.

Esta situación se puede resolver de diferentes maneras.

En casa, piensa en una estrategia que te permita contestar la pregunta del problema. También realiza una estimación de la cantidad de metros que los jugadores recorren en su calentamiento. Registra esto en tu cuaderno.

Hay que resolver esta situación.

Primero hay que calcular cuántas yardas recorren los jugadores al dar dos vueltas al campo y, posteriormente, realizarás la conversión a metros.

Para iniciar a dar respuesta al problema, puedes establecer que dar una vuelta al campo equivale a calcular el perímetro del campo de juego. El perímetro de una figura se obtiene sumando las medidas de todos sus lados. En este caso el perímetro del campo, que es un rectángulo, es igual a la suma de 53 punto 3 más 120, más 53 punto 3, más 120, yardas. También se puede decir que el perímetro es igual a 2 por 53 punto 3 yardas más, 2 por 120 yardas.

Al resolver las multiplicaciones o eliminar paréntesis, se obtiene que él, perímetro es igual a 106 punto 6 yardas más 240 yardas. Efectuando la suma se obtiene que el perímetro es igual a 346 punto 6 yardas, que es lo que se recorre al dar una vuelta al campo. Sin embargo, ya que los jugadores darán dos vueltas al campo, entonces, se multiplica 2 por 346 punto 6 yardas, de lo que se obtiene que los jugadores recorrerán 693 punto 2 yardas en su calentamiento.

Ahora vas a realizar la conversión de las yardas obtenidas a metros, que es la unidad en que se solicita la respuesta al problema.

Sabes que una yarda equivale a 91 punto 4 centímetros. Como la respuesta se solicita en metros y sabes que 100 centímetros equivalen a 1 metro; entonces, se divide 91 punto 4 centímetros entre 100 de lo que resulta que, 91.4 centímetros equivalen a cero punto 914 metros.

Se establece la otra relación, como se muestra en la tabla, donde 1 yarda equivale a 0.914 metros, y 693 punto 6 yardas equivalen a “x” metros.

Se puede plantear una regla de tres, de donde se tiene que “x” es igual a 693 punto 2 yardas por cero punto 914 metros, entre una yarda. Aquí se simplifican las unidades “yardas” que se encuentran tanto en el denominador como en el numerador.

Al efectuar la multiplicación resulta “x” igual a 633 punto 5 848 metros, entre uno, cuyo cociente es 633 punto 5 848 metros.

Por lo que se concluye que los jugadores recorrerán 633 punto 58 metros para su calentamiento, truncando en valor de “x” en los centésimos, que representan los centímetros.

Regresa a tu estimación hecha al inicio de este problema.

¿Qué tan acertada fue? ¿Por qué piensas que ocurrió lo anterior?

Con respecto a la estrategia que pensaste, ¿fue parecida a la que utilizaste?

Ahora, revisa otro caso en donde es necesario hacer una conversión.

Juan visitó Estados Unidos. Ese viaje lo realizó en su automóvil donde él puede leer la magnitud de la velocidad en kilómetros por hora. Al entrar a ese país observó un señalamiento que indica debe ir a una velocidad máxima de 60 millas por hora.

Velocidad máxima: 60 mi/h

¿Cuál es la velocidad máxima permitida en esa zona, en kilómetros por hora?

Escribe una estimación de esa velocidad.

Ahora hay que resolver el problema.

Una manera de resolver es ordenar los datos. Ten en cuenta que 1 milla es equivalente a 1 punto 609 kilómetros, entonces, 60 millas equivalen a “x” kilómetros.

Puedes ahora establecer una regla de tres de donde se tiene que “x” es igual a 60 millas por 1 punto 609 kilómetros, entre una milla. Puedes simplificar la unidad “millas”, que se encuentran en el numerador y en el denominador. Así que “x” es igual a 60 por 1 punto 609 kilómetros, entre 1.

Al efectuar las operaciones se obtiene que “x” es igual a 96 punto 54 kilómetros. Por lo tanto, la velocidad máxima a la que debe manejar Juan es de 96 punto 54 kilómetros por hora.

Ahora, regresa a tu estimación.

¿Qué tanto se aproximó tu estimación al resultado que se obtuvo aquí?

Recuerda que puedes usar otro método de resolución ya que, en las matemáticas, los resultados se pueden obtener de diversas maneras. Lo importante es comprender lo que se te pide en cada situación problema.

Se espera que, con lo estudiado, puedas resolver diversos problemas donde se requieran conversiones entre unidades del Sistema Internacional de Unidades y del Sistema Inglés.

Recuerda que el éxito no se logra superando a los demás, sino superándote a ti mismo.

El reto de hoy:

Se te invita a resolver el siguiente reto.

El árbol de nombre General Sherman, de la especie Secuoya Gigante se encuentra ubicado en un parque de California, Estados Unidos y es considerado el árbol de mayor volumen en el mundo. Si se sabe que su altura es de 8.38 decámetros.

1. ¿Cuál es su altura en yardas?

Resuelve tu reto, guarda tus evidencias y compártelas con tu profesora o profesor a la distancia.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html