Reparto proporcional
Reparto proporcional
Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.
Énfasis: resolver problemas de reparto proporcional.
¿Qué vamos a aprender?
Anteriormente has aprendido a identificar cuándo una situación es de proporcionalidad directa a través del reconocimiento de sus propiedades, en una situación de proporcionalidad directa, la constante de proporcionalidad es un número, siempre el mismo.
En esta sesión, conocerás cómo resolver problemas de reparto proporcional aplicados a situaciones de la vida cotidiana.
¿Qué hacemos?
Para comenzar con la resolución de problemas de reparto proporcional, reflexiona en las siguientes preguntas:
- ¿Qué es el reparto proporcional?
- ¿Cómo se resuelve un problema de reparto proporcional?
- La constante de proporcionalidad directa, ¿ayuda en la resolución de problemas de reparto proporcional?
Registra tus ideas, producto de tus reflexiones. Más adelante las podrás validar o enriquecer.
¿Cómo se define el reparto proporcional?
El significado asociado a la palabra “repartir” implica dividir el todo entre tantos elementos como sea necesario. Repartir proporcionalmente significa asignar una parte proporcional del todo con relación a una cantidad.
Por ejemplo, si en un convivio se necesita repartir una gelatina entre 5 familias, el reparto se puede hacer de distintas maneras sin importar que unas rebanadas sean más grandes que otras.
Pero si se hace un reparto proporcional de la gelatina con relación a la cantidad de integrantes de cada familia, se necesita cortarla en tantas rebanadas iguales como personas haya, y asignar una rebanada a cada integrante.
Dicho lo anterior, presta atención a el primer problema.
De acuerdo con el informe “El estado de los plásticos 2018” de ONU Ambiente, alrededor de 13 millones de toneladas de plástico son vertidas en los océanos cada año. Esta contaminación tiene consecuencias sobre el medio ambiente; por ejemplo, se estima que cada año están muriendo más de un millón de aves y más de 100,000 mamíferos marinos a consecuencia de los plásticos que llegan al océano.
Los datos anteriores han favorecido que diversas organizaciones presentaran y desarrollaran programas sobre la limpieza en las playas. En el caso particular de la cooperativa “México Saludable”, se organizó una rifa, y con lo recaudado se pretende adquirir las herramientas para hacer más eficiente la limpieza de las playas.
Analiza un caso específico que se vincula con el tema de estudio de esta sesión.
Problema 1
Cinco personas compraron un boleto para la rifa organizada por “México Saludable” y ganaron $4 000. La primera persona cooperó con $10; la segunda, con $50; la tercera, con $20; la cuarta, con $80, y la última, con $40.
¿Cuánto le toca del premio a cada persona?
Una forma de repartir el premio es dividir los $4 000 entre el total de las personas que cooperaron para la compra del boleto, es decir, 5 personas. A cada una le tocan $800.
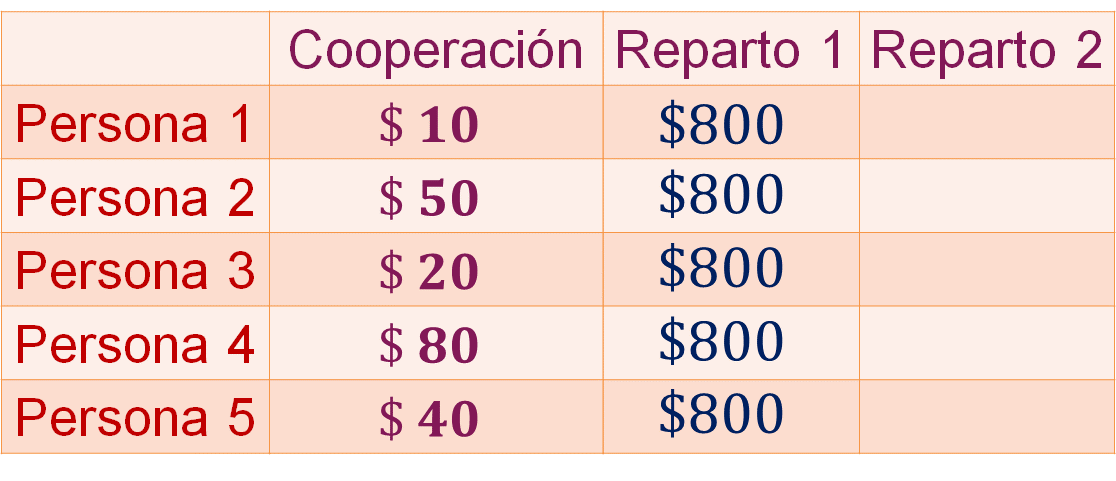
¿Consideras que el reparto es justo?, ¿qué piensas?
Si el premio se reparte de forma proporcional a la cantidad de dinero que aportó cada persona, se tiene otra forma de repartir el premio. Observa con atención.
Lo primero que harás es sumar el monto con que cooperó cada una de las personas.
Cooperación = 10 + 50 + 20 + 80 + 40 = 200
Ya tienes el dato del premio de la rifa, que es igual a $4 000.00, y las cooperaciones de las personas, que es igual a 200 pesos.
Premio de la rifa = $4,000
Cooperación = 200
Ahora calcula la constante de proporcionalidad directa, que se denomina con la letra “k”. La constante de proporcionalidad es igual a 4,000 entre 200, cuyo cociente es igual a 20
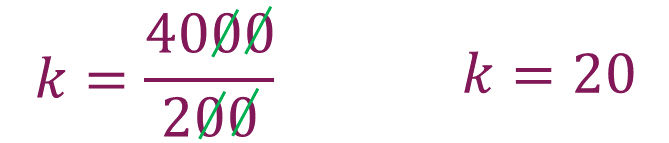
Ya cuentas con la constante de proporcionalidad (“k”), que es igual a 20. Ahora calcula cuanto le corresponde a cada persona.
Persona 1:
Para calcular el segundo valor de la magnitud “y”, para primera persona, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de la primera magnitud correspondiente. Sustituyendo valores, “y” es igual a 20 por 10. Y se obtiene como resultado, “y” es igual a 200
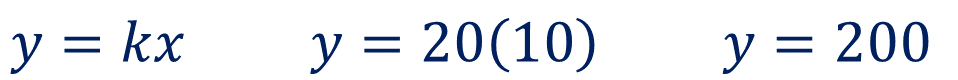
A la primera persona le corresponden 200 pesos por la aportación que dio para la compra del boleto.

Persona 2:
El valor de la constante de proporcionalidad es igual a 20, y la segunda persona cooperó con 50 pesos para comprar el boleto, por lo que ahora calcularás cuánto le toca a esta segunda persona.
Para calcular el segundo valor de la magnitud “y”, lleva a cabo el siguiente producto. Multiplica la constante de proporcionalidad por el valor de la cooperación correspondiente. Sustituyendo valores, “y” es igual a 20 por 50. Y se obtiene como resultado, “y” es igual a 1,000

A la segunda persona le tocan 1,000 pesos por la aportación que dio para la compra del boleto.

Persona 3:
Para calcular lo que recibió la persona 3, tomarás el valor de la constante de proporcionalidad, que es igual a 20, y la tercera persona cooperó con 20 pesos para comprar el boleto.
Lleva a cabo un producto entre la constante de proporcionalidad por el valor de la cooperación correspondiente para calcular el segundo valor de la magnitud.
Sustituyendo valores, “y” es igual a 20 por 20. Se obtiene como resultado que “y” es igual a 400

A la tercera persona le tocan 400 pesos por la aportación que dio para la compra del boleto.

Ahora calcula lo que recibió la cuarta persona.
Persona 4:
Sabes que el valor de la constante de proporcionalidad es igual a 20, y la cuarta persona cooperó con 80 pesos para comprar el boleto; determina cuánto le toca a esta cuarta persona.
Para calcular el segundo valor de la magnitud “y”, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de la cooperación correspondiente. Sustituyendo valores, “y” es igual a 20 por 80. Y se obtiene como resultado, “y” es igual a 1,600

A la cuarta persona le tocarán 1 000 pesos por la aportación que dio para la compra del boleto.

Para terminar el problema, calcula lo que recibió la quinta persona.
Persona 5:
Dado que el valor de la constante de proporcionalidad es igual a 20, y la quinta persona cooperó con 40 pesos para comprar el boleto, determina cuánto le tocará a esta persona.
Para calcular el segundo valor de la magnitud “y”, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de la cooperación correspondiente.
Sustituyendo valores, “y” es igual a 20 por 40. Se obtiene como resultado que “y” es igual a 800

A la quinta persona le tocan 800 pesos por la aportación que dio para la compra del boleto.

Repartir de forma proporcional, tomando en cuenta la cantidad con la que cooperó cada persona para la compra del boleto.
Al sumar los montos que le corresponden a cada persona, se sabe que el total es $4 000:

Como puedes observar, este reparto es proporcional a lo que cada uno cooperó. De esta manera, el reparto es justo.
Ahora, continúa con el tema y analiza el siguiente caso.
Problema 2
Como parte de los proyectos de las organizaciones que promueven el acceso a la lectura, se piensa construir una biblioteca en un terreno de cien metros cuadrados y estará dividida como se muestra en la siguiente imagen.
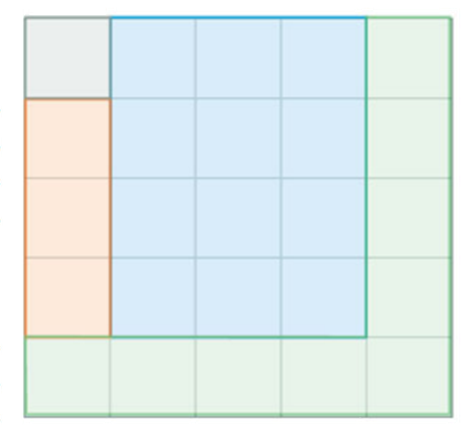
- En la región gris estará el sanitario.
- La zona anaranjada será la recepción.
- En la zona azul estarán los libreros.
- Y la región verde será la zona destinada a la lectura.
Determina el área que corresponde a cada lugar.
Observa los cuadrados que corresponden a cada zona. En la zona gris se encuentra solamente 1 cuadro; en la zona naranja, 3; la azul, 12; y la verde, 9. En total hay 25 cuadrados.
Ahora, organiza los datos en un registro tabular, ya sabes cuántos cuadros de cada color hay y que en total son 25
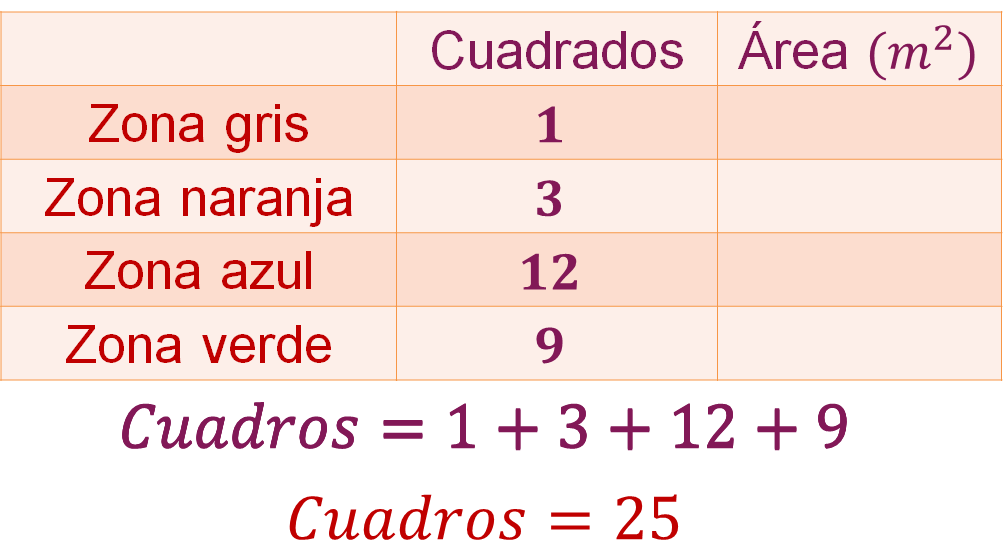
El área del terreno para la biblioteca es igual a 100 metros cuadrados, y la suma de los cuadrados que ocuparán las 4 zonas es igual a 25
Observa que la constante de proporcionalidad directa es igual a 100 entre 25; realizando la operación da igual a 4

Para calcular el segundo valor de la magnitud “y”, se llevará a cabo un producto para cada zona. Comienza con la zona gris.
Zona gris:
Multiplica la constante de proporcionalidad por el valor de la primera magnitud correspondiente. Sustituyendo valores, “y” es igual a 4 por 1, que es el cuadrado. Se obtiene como resultado “y” es igual a 4
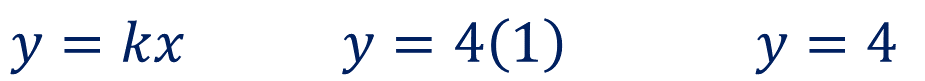
La zona gris que corresponde al sanitario ocupará un área de 4 metros cuadrados.

Zona naranja:
Retomando que el valor de la constante de proporcionalidad es igual a 4 y la zona naranja tiene 3 cuadrados, calcula el área que ocupará.
Para obtener el segundo valor de la magnitud “y”, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de los cuadrados correspondientes. Sustituyendo valores, “y” es igual a 4 por 3. Se obtiene como resultado “y” es igual a 12
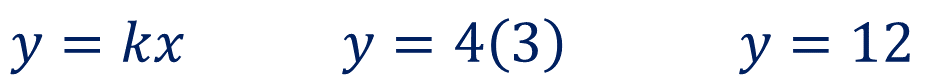
La zona naranja, que corresponde a la recepción, ocupará un área de 12 metros cuadrados.

Continúa con la siguiente zona.
Zona azul:
Para calcular el área de la zona azul, toma el valor de la constante de proporcionalidad, que es igual a 4, y la zona azul cuenta con doce cuadros; así obtendrás el área que ocupará.
Lleva a cabo un producto entre la constante de proporcionalidad por el valor de los cuadrados correspondientes para calcular el segundo valor de la magnitud. Sustituyendo valores, “y” es igual a 4 por 12. Se obtiene como resultado “y” es igual a 48
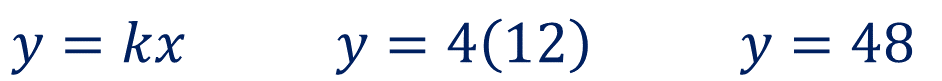
La zona azul, que corresponde a los libreros, ocupará un área de 48 metros cuadrados.
Para terminar el problema calcula el área de la zona verde.
Zona verde:
El valor de la constante de proporcionalidad es igual a 4, y la zona verde cuenta con 9 cuadros; calcula el área que ocupará.
Para obtener el segundo valor de la magnitud “y”, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de los cuadrados correspondientes. Sustituyendo valores, “y” es igual a 4 por 9. Se obtiene como resultado “y” es igual a 36
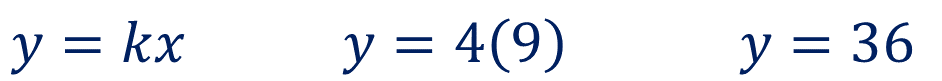
La zona verde, que corresponde al espacio de lectura, ocupará un área de 36 metros cuadrados.

Para comprobar, suma el área de cada zona: 4 metros cuadrados que ocuparán los sanitarios, más 12 metros cuadrados que ocupará la recepción, más 48 metros cuadrados que ocuparán los libreros, más los 9 metros cuadrados de la zona de lectura. Obteniendo como resultado los 100 metros cuadrados destinados para la construcción de la biblioteca.

Analiza un tercer problema.
Problema 3
En un restaurante trabajan 5 cocineros y 3 meseros con diferentes horarios. Dos cocineros y dos meseros trabajan 8 horas al día, un cocinero y un mesero trabajan 6 horas al día y los siguientes cocineros trabajan 3 y 4 horas al día, respectivamente.
Lo que se junta en propinas se lo reparten cocineros y meseros en proporción a la cantidad de horas que trabajan. Si el total de propinas en un día fue de $15,750, ¿cuánto le tocará a cada uno?
Lo primero que harás, será sumar las horas que trabajó cada cocinero y cada mesero. Los cocineros trabajaron 8 más 6, más 4, más 3 horas cada uno en el transcurso del día, y los meseros trabajaron 8 horas más 6 horas durante el día. Sumando, da un total de 35 horas.
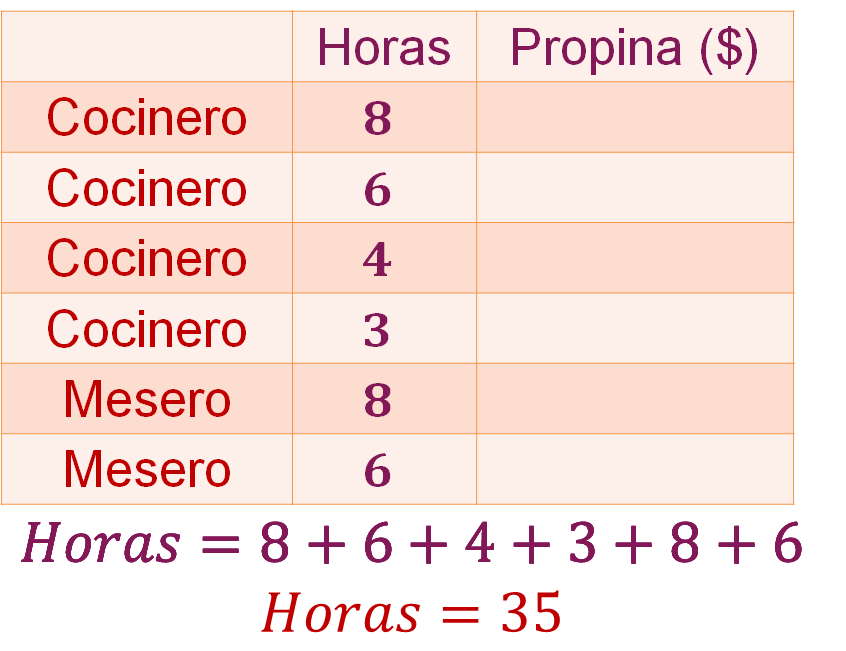
Ya que tienes el total de las horas trabajadas por los cocineros y meseros, calcularás la constante de proporcionalidad directa “k”, ya que se tiene la propina que reciben durante el día y las horas totales trabajadas por los cocineros y meseros.
La constante de proporcionalidad directa es igual a 15,750 entre 35; realizando la división, el cociente es igual a 450

Para calcular el segundo valor de la magnitud “y”, llevarás a cabo un producto para cada mesero y cocinero. Comienza con el mesero y cocinero que trabajan 8 horas.
Cocinero y mesero – 8 horas:
Multiplica la constante de proporcionalidad por el valor de las horas correspondientes. Sustituyendo valores, “y” es igual a 450 por 8. Se obtiene como resultado “y” es igual a 3,600

El cocinero y el mesero que trabajan 8 horas recibirán, cada uno, 3,600 pesos.

Cocinero y mesero – 6 horas:
Retomando que el valor de la constante de proporcionalidad es igual a 450, y las horas que trabajan los cocineros y meseros son 6 horas, calcula la propina que recibirá cada uno.
Para obtener el segundo valor de la magnitud “y”, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de las horas correspondientes. Sustituyendo valores, “y” es igual a 450 por 6. Se obtiene como resultado que “y” es igual a 2 700

El cocinero y el mesero que trabajan 6 horas recibirán, cada uno, 2,700 pesos.

Cocinero – 4 horas:
Para calcular la propina que recibirá el cocinero que trabajó 4 horas, tomarás el valor de la constante de proporcionalidad, que es igual a 450, y las 4 horas que laboró.
Lleva a cabo un producto entre la constante de proporcionalidad por el valor de las horas correspondientes para calcular el segundo valor de la magnitud. Sustituyendo valores, “y” es igual a 450 por 4. Se obtiene como resultado que “y” es igual a 1,800

El cocinero que trabajó 4 horas recibirá 1,800 pesos.

Para terminar el problema, calcula la propina que recibió el cocinero que trabajó 3 horas.
Cocinero – 3 horas:
El valor de la constante de proporcionalidad es igual a 450, y las horas que trabajó el cocinero durante el día fueron 3 horas. Para obtener el segundo valor de la magnitud “y”, lleva a cabo un producto. Multiplica la constante de proporcionalidad por el valor de las horas correspondientes. Sustituyendo valores, “y” es igual a 450 por 3. Se obtiene como resultado, “y” es igual a 1,350

El cocinero que trabajó 3 horas recibirá 1,350 pesos.

Para comprobar, suma la propina que reciben el cocinero y mesero que trabajan 8 horas, más la propina que reciben el cocinero y mesero que trabajan 6 horas, más la propina que recibe el cocinero que trabaja 4 horas, más la propina que recibe el cocinero que trabaja 3 horas. Obteniendo como resultado 15,750 pesos, que fue el total de la propina que juntaron en ese día.
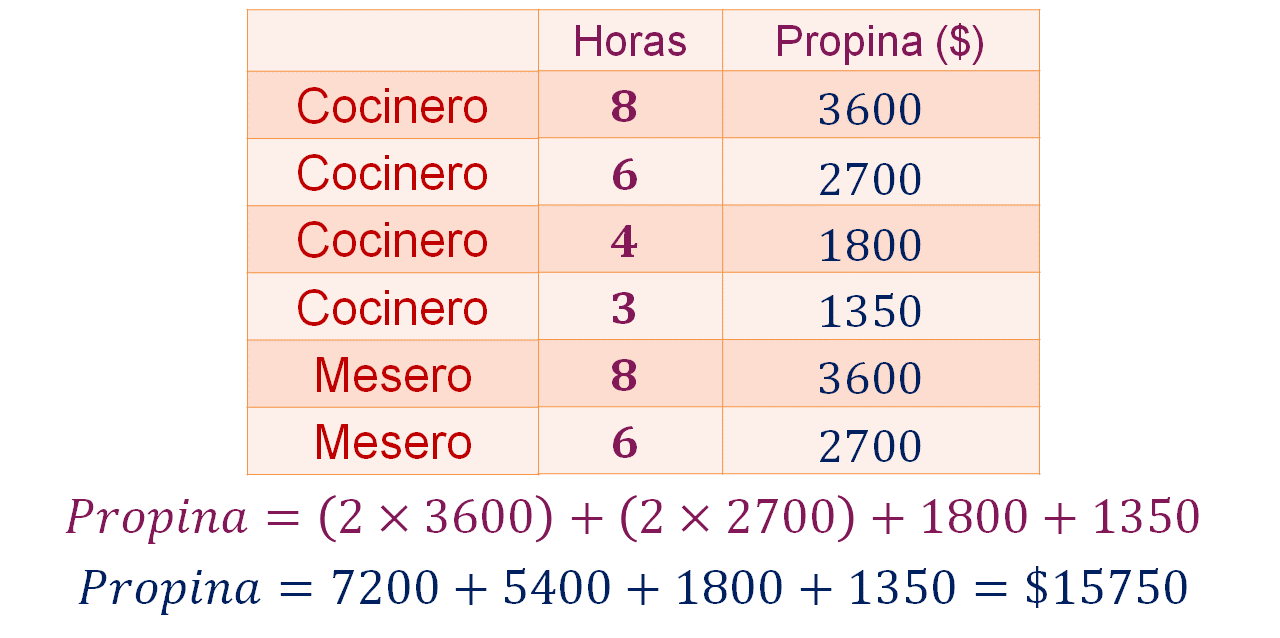
En esta sesión comprendiste cómo calcular el reparto proporcional usando ejemplos cercanos a la vida cotidiana.
Consulta tu libro de texto de Matemáticas de segundo grado, seguramente encontrarás otras actividades para profundizar en este tema.
El reto de hoy:
Con lo aprendido en esta sesión, resuelve el siguiente problema de reparto proporcional.
Problema
En una pensión de animales hay tres perros que pesan: uno 20 kg, el otro 10 kg y el último 5 kg. Si se contempla que 70 kg de alimento dura dos meses, ¿qué cantidad de alimento le corresponde a cada perro?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas