Relaciones entre operaciones y números racionales
Relaciones entre operaciones y números racionales
Aprendizaje esperado: resuelve problemas de multiplicación y división con fracciones y decimales positivos.
Énfasis: dar sentido y significado a las propiedades de las operaciones y los números racionales.
¿Qué vamos a aprender?
Profundizarás en los números racionales (fracciones) y sus operaciones básicas. Esta sesión, te ayudará a reconocer relaciones sorprendentes que te servirán para comprender mejor este tipo de números y favorecer así el desarrollo de tu “sentido numérico”.
¿Qué hacemos?
Para iniciar con el tema de esta sesión, analiza la siguiente información que se enfoca en la noción de los números racionales (fracciones).
Con el paso del tiempo, la humanidad ha conseguido resolver diferentes problemas gracias al ingenio y la creación matemática. Uno de los problemas más complejos para el ser humano fue encontrar una manera de medir de forma precisa. Los números naturales, permiten contar y comparar colecciones finitas de objetos. Pero en la vida cotidiana no basta con contar objetos individuales, también hay que medir, como, por ejemplo, la longitud, el área, la masa, el peso o el tiempo.
Al medir no siempre se obtiene una unidad entera. Resolver el problema requiere del desarrollo de una extensión en los sistemas numéricos, es decir, los números racionales, también conocidos como fracciones. Éstos permiten solucionar problemas en los que los números naturales no son suficientes.
Por ejemplo, el tiempo. El tiempo se mide en horas, pero no siempre se utilizan horas completas para realizar las actividades, regularmente se utilizan “partes” de hora, incluso se usan expresiones como “media hora” o “un cuarto de hora”. Lo mismo sucede cuando se quiere conocer con mayor precisión el peso de un objeto o una distancia: se usan números racionales.
Los números racionales tienen propiedades únicas que los hacen diferentes de los demás conjuntos numéricos.
Una fracción generalmente es un número que se puede expresar de la forma “a sobre b”, considerando que tanto ‘a’ como ‘b’ sean números naturales y siempre que ‘b’ sea diferente de cero. Los elementos de la fracción son el numerador y el denominador, y generalmente el denominador indica en cuántas partes iguales se está dividiendo a la unidad, mientras que el numerador indica el número de partes que se están considerando de la unidad.

Cuando se quiere medir una longitud que no coincide con un número entero, entonces se debe considerar la partición de la unidad con la que se está midiendo.
Se debe tener en cuenta que la división de la unidad (en este caso un entero) se debe hacer en partes iguales, considerando el denominador de cada fracción.
La mejor aproximación de una medida se dará en función del número de particiones que se hagan de la unidad. Esto lleva a pensar en la propiedad de densidad de las fracciones.
Observen que, a partir de la construcción de una fracción, se pueden generar otras.

Por ejemplo, considera la división de la unidad en 2 partes iguales. A continuación, una de esas partes se vuelve a dividir en 2 partes iguales. Si se repite ese proceso se siguen encontrando fracciones. Esto permite entender que entre dos fracciones cualesquiera existe siempre otra fracción.
La propiedad de densidad establece una diferencia entre la naturaleza de los números racionales con respecto a la de los números naturales. En el orden de los números naturales, se puede indicar cuál es el sucesor o el antecesor de un número. En los racionales esto ya no es tan simple.
También te puedes dar cuenta de que las particiones nuevas le dan nuevos nombres a las fracciones que ya estaban ubicadas en la recta numérica. Esta es la idea de equivalencia, otra diferencia notable con respecto a los números naturales.
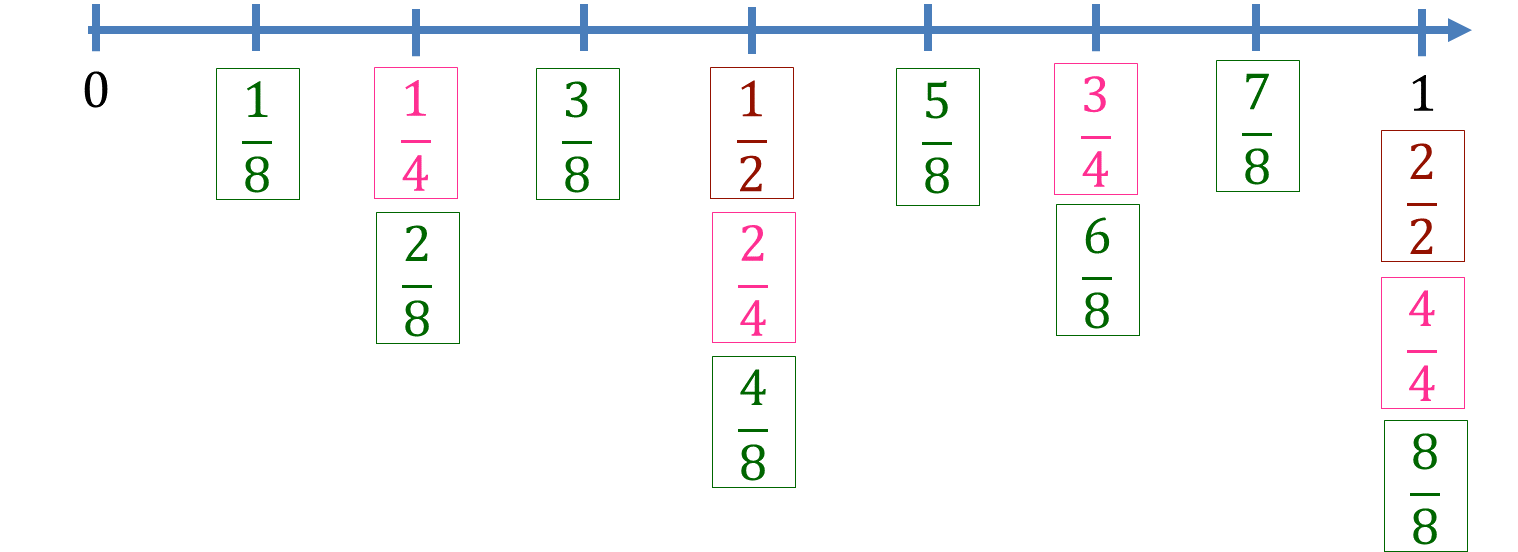
El mismo número fraccionario puede tener diferentes “representaciones y nombres”, y ellos tener el mismo valor. Esta idea de equivalencia es fundamental a la hora de hacer adición o sustracción de fracciones que tienen diferente denominador.
Ya conoces cómo realizar estas operaciones, por lo tanto, revisa las siguientes oraciones numéricas para identificar relaciones y clarificar las propiedades de la adición en números racionales.
En la siguiente tabla se ha registrado una familia de ocho oraciones numéricas y una de ellas está resuelta, la suma “un cuarto más tres dieciseisavos, es igual a cuatro dieciseisavos más tres dieciseisavos, es igual a siete dieciseisavos”.
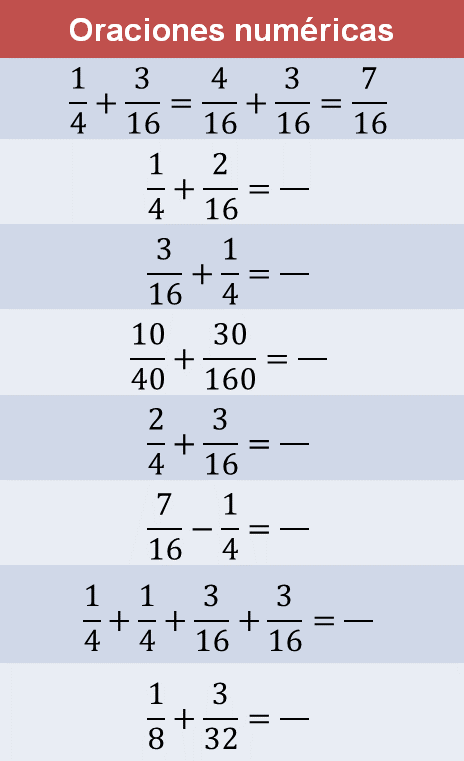
Observa que, para llevar a cabo la adición de fracciones con diferente denominador, se utiliza la equivalencia de fracciones. En este caso, un cuarto es equivalente a cuatro dieciseisavos. Como las fracciones tienen el mismo denominador, entonces se efectúa la suma de los numeradores.
Dado que es una familia de operaciones:
¿Esta oración inicial ayuda con la resolución de las demás operaciones?
De ser así, ¿cómo es la ayuda?
Apóyate en la operación resuelta para encontrar formas que te faciliten la resolución de éstas y otras operaciones con números racionales.
Ahora, resuelve las operaciones restantes.
Antes de verificar los resultados, analiza y comprende lo que hizo Jorge, estudiante de segundo de secundaria, en la Ciudad de México.
Jorge desarrolla las operaciones sin considerar la oración resuelta y usa un procedimiento que lo lleva a un resultado erróneo. Por un lado, suma directamente los numeradores y coloca el resultado en el numerador, por otro, conserva el denominador mayor en el denominador del resultado. Esta resolución evidencia que no se considera la necesidad de que los denominadores sean iguales para poder sumar las fracciones, es decir, no se está tomando en cuenta la equivalencia de fracciones como medio para hacer esta suma posible.

Ese procedimiento lo repite en cada oración numérica. En “un cuarto más dos dieciseisavos” hace la suma de los numeradores y el resultado lo coloca como numerador, es decir, tres. Se deduce que elige el denominador de mayor valor para colocarlo en el denominador del resultado, en el primer caso, dieciséis. En la cuarta línea hace lo mismo. Diez más treinta son cuarenta, lo coloca en el numerador. Ciento sesenta es más grande que cuarenta, lo coloca en el denominador.
En la sexta oración, se revela que el alumno extiende el procedimiento a la sustracción de fracciones. “Siete dieciseisavos menos un cuarto, es igual a seis dieciseisavos”, coloca la resta de los numeradores en el numerador y conserva el denominador mayor en su resultado.
Al resolver la expresión que involucra cuatro sumandos, inicia con sumas parciales de las fracciones que se repiten, pero una vez más considera que, un cuarto más un cuarto es igual a dos dieciseisavos. La suma de dos dieciseisavos más seis dieciseisavos es igual a ocho dieciseisavos, pero la suma inicial no considera la propiedad de equivalencia de los números racionales, por lo que no es correcta.
¿Tuviste alguna dificultad, como fue en el caso de Jorge?
Es importante entender que el error es una oportunidad para aprender. Por tanto, cuando realices alguna actividad matemática debes expresar las dificultades o dudas que tengas, así pueden ser aclaradas y corregidas para lograr el aprendizaje.
¿Utilizaste la operación resuelta?
¿En qué forma te fue útil?
Ahora, analiza las oraciones numéricas y determina la utilidad de la oración resuelta. Busca revelar los patrones entre los números y las operaciones, hay relaciones que a veces están “escondidas”, por lo que debes identificarlas.
Segunda oración numérica 1/4 + 2/16:

Compara el primer sumando de cada una de las dos oraciones numéricas, como resultado se identifica que los dos sumandos, un cuarto y un cuarto, son iguales.
Ahora compara el segundo sumando de cada una de las dos oraciones numéricas, tres dieciseisavos y dos dieciseisavos. Estos números fraccionarios no son iguales, pero tienen el mismo denominador, por lo que pertenecen al mismo tipo de fracciones. Observa los numeradores. Se deduce que la diferencia entre estos dos numeradores es un dieciseisavo.

Por lo tanto, la oración numérica resulta es útil, pues al resultado, es decir, a la suma le puedes restar un dieciseisavo, y de esta manera se puede decir que un cuarto más dos dieciseisavos es igual a seis dieciseisavos, que es el resultado de la segunda oración numérica.

Como puedes darte cuenta, hasta el momento no se realizó una suma desarrollada. Lo que se hizo fue comparar los sumandos, identificar la relación entre ellos y determinar cómo esta relación afecta al resultado. Eso ayudó a obtener el resultado correcto.
Fue de utilidad analizar los sumandos que tienen el mismo denominador e identificar que los numeradores se diferenciaban en un dieciseisavo. También se conoce que un cuarto es equivalente a cuatro dieciseisavos, por lo que ya no es necesario el desarrollo con la fracción equivalente.
Comparemos la siguiente pareja de oraciones numéricas.
Tercera oración numérica 3/16 + 1/4:
¿Qué identificas?

Los sumandos de ambas oraciones numéricas son los mismos, pero el orden es diferente.
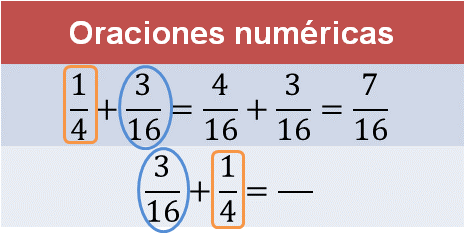
Por lo tanto, el resultado es el mismo. Has obtenido la suma sin hacer cálculos, y lo has logrado al favorecer el desarrollo de tu sentido numérico.

Las habilidades de análisis y comparación te ayudan a avanzar en el conocimiento de los números y las operaciones. Observa qué otras relaciones se identifican en la familia de oraciones numéricas.
Cuarta oración numérica 10/40 + 30/160:
En este caso, ¿qué identificas al comparar los sumandos?

La comparación de los sumandos de cada una de las oraciones numéricas permite identificar que el primer sumando de la cuarta oración es equivalente al primer sumando de la primera: tanto el numerador como el denominador se han multiplicado por diez.
Lo mismo está ocurriendo con los segundos sumandos. Al tener fracciones equivalentes multiplicadas por diez, se deduce que el resultado de la cuarta oración también será una fracción equivalente al resultado de la primera, con la cualidad de que tanto el numerador como el denominador se multiplican por diez.
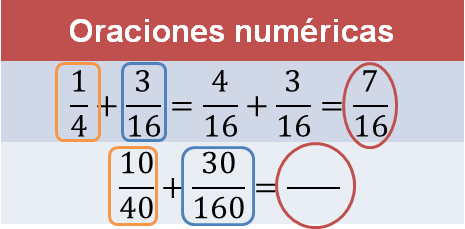
Por lo tanto, si multiplicas el resultado de la primera oración numérica por 10, obtendrás el resultado de la cuarta oración:

Hasta este momento, has resuelto las operaciones basándote en la comparación entre los números, el análisis de los efectos de las operaciones y la idea de equivalencia, con lo que se fortalecen los significados entre las operaciones con números racionales. Analiza el siguiente caso.
Quinta oración numérica 2/4 + 3/16:
¿Qué ocurre al contrastar los sumandos?

Al comparar el segundo sumando de cada una de las dos oraciones numéricas se identifica que se tienen tres dieciseisavos en ambos casos, es decir, estos números son iguales.
Ahora, el primer sumando de cada una de las dos oraciones numéricas es diferente, aunque al tener el mismo denominador, pertenecen al mismo tipo de fracciones.

El numerador del primer sumando de la segunda oración es el doble que el numerador del primer sumando de la primera. Entonces, se puede usar la equivalencia. Si un cuarto es equivalente a cuatro dieciseisavos, entonces dos cuartos será el doble de este último, es decir, ocho dieciseisavos.
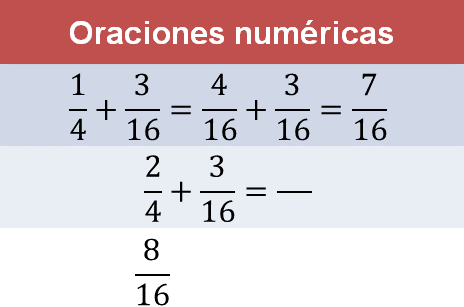
Tienes la respuesta, la suma de ocho dieciseisavos con tres dieciseisavos es once dieciseisavos. La primera oración resuelta vuelve a ser útil.
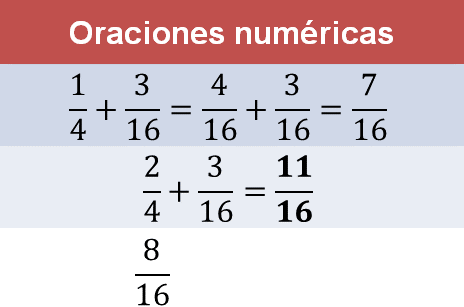
Ahora, analiza una sustracción o resta de fracciones. Se puede diferenciar a las sumas de las restas, no sólo por las características de sus símbolos, sino por los significados que se le han asociado. El ejercicio lo puedes resolver centrándote en la relación inversa que hay entre ellas.
Sexta oración numérica 7/16 – 1/4:

Se reconoce que en ambas operaciones aparecen los mismos números; sin embargo, tanto el signo de la operación, como el orden en el que se encuentran, determinan el efecto de éstos al resolver la oración numérica.
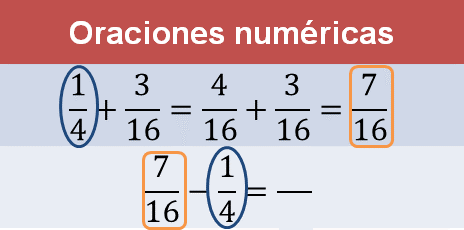
Una manera de resolver la sustracción es pensar: ¿qué número se puede sumar a un cuarto para que el resultado sea siete dieciseisavos? Si se sabe que un cuarto más tres dieciseisavos es igual a siete dieciseisavos, entonces se puede relacionar a tres dieciseisavos como el resultado de la sustracción.
Mientras que en la primera operación numérica tres dieciseisavos es un sumando y el efecto del operador es juntar, en la otra oración numérica es la diferencia que resulta de siete dieciseisavos menos un cuarto.
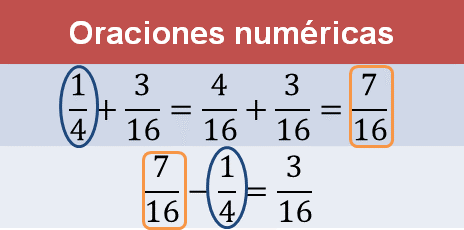
Con las reflexiones anteriores, reconociste relaciones entre los números y las operaciones. Analiza los últimos casos.
Séptima oración numérica 1/4 + 1/4 + 3/16 + 3/16:
Una vez más, compara los sumandos de las oraciones numéricas, ¿y qué identificas?
Anota lo que observas.

En este caso, tanto el primero como el segundo sumando aparecen dos veces y son iguales, por lo tanto, para resolver la segunda operación puedes pensar en sumar dos veces siete dieciseisavos o multiplicarlo por dos y, con ello, obtener el resultado correcto, que es catorce dieciseisavos.
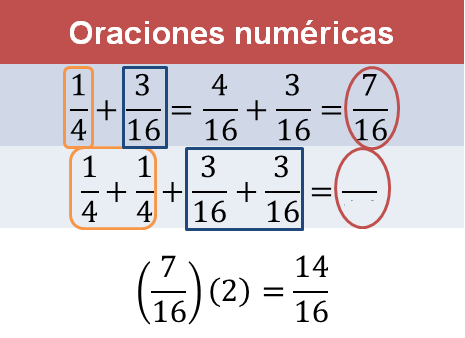
Catorce dieciseisavos es el doble de siete dieciseisavos o siete dieciseisavos es la mitad de catorce dieciseisavos.

Observa el último caso.
Octava oración numérica 1/8 + 3/32:

Al comparar los sumandos, puedes identificar que un octavo es la mitad de un cuarto, o que un cuarto es el doble de un octavo. Se puede multiplicar un cuarto por un medio para comprobarlo.
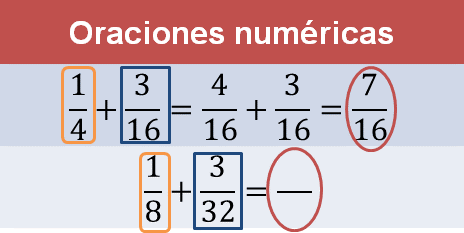
La multiplicación de fracciones tiene ese sentido, es decir, “un medio de un cuarto”. Numéricamente, basta con multiplicar numerador por numerador, ese producto se coloca en el numerador. Se procede de la misma forma con los denominadores, se obtiene el producto y se coloca en el denominador del resultado.
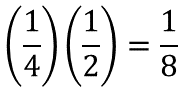
El mismo razonamiento aplica a los segundos sumandos, tres treintaidosavos es la mitad de tres dieciseisavos o tres dieciseisavos es el doble de tres treintaidosavos.
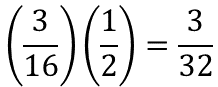
Como los dos sumandos son la mitad de los sumandos originales, el resultado de la segunda oración se puede obtener al demediar (o sacar mitad del resultado de) la oración inicial, siete dieciseisavos. Es decir, multiplicar siete dieciseisavos por un medio, cuyo producto es siete treintaidosavos.

Recapitula lo que has estudiado para formalizar algunas de las propiedades que se han utilizado al resolver las oraciones numéricas. La intención es comprender las relaciones entre los números racionales y sus operaciones. Observa con atención el siguiente cuadro:

Como pudiste darte cuenta, la oración numérica resuelta fue de ayuda para resolver las demás oraciones numéricas de la familia. Por lo tanto, se pueden usar las propiedades de las operaciones para resolver otras oraciones numéricas, de igual o mayor complejidad.
Los números racionales o fracciones se pueden sumar sólo cuando pertenecen al mismo tipo de fracción, es decir, cuando tienen el mismo denominador. Para ello, comprender la equivalencia de fracciones facilita el trabajo operacional con estos números.
También es necesario reflexionar sobre la propiedad conmutativa y la propiedad distributiva de la adición, ya que permite mejorar tus habilidades en la resolución de este tipo de operaciones. Analizar los ejemplos y tratar de identificar las relaciones numéricas permite comprender el tema.
Has concluido la sesión. Para profundizar en el tema, consulta tu libro de texto de segundo de secundaria.
El reto de hoy:
Aplica lo que has aprendido y resuelve las siguientes oraciones numéricas:
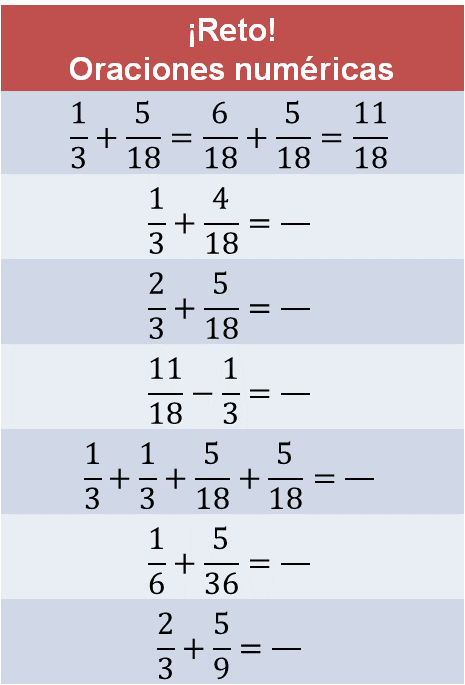
Se tiene una familia de siete oraciones numéricas y una de ellas está resuelta: un tercio más cinco dieciochoavos es igual a seis dieciochoavos más cinco dieciochoavos, lo que es igual a once dieciochoavos.
Con el apoyo de la oración resulta, resuelve las siguientes oraciones.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/