Regla del producto II
Regla del producto II
Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: resolver problemas reales que impliquen el uso de la regla del producto.
¿Qué vamos a aprender?
Los materiales que necesitarás son tu cuaderno de apuntes, un lápiz y goma.
Conoces o has tenido experiencias de aprendizaje sobre la regla del producto, que hace referencia a la probabilidad de que ocurran dos eventos a la vez.
Pero, ¿qué conceptos se requieren para resolver problemas aplicando la regla del producto?
Uno de los conceptos para considerar es el de: Probabilidad, que es una forma de medir la posibilidad de que un evento ocurra.
Se sabe que la medida de la probabilidad es un valor entre cero y uno, lo que incluye a los valores de 0 y 1 como posibles resultados.
Otro concepto es el de “evento”, que se refiere al posible resultado en un experimento aleatorio.
Regularmente se le representa por las primeras letras del abecedario y en mayúsculas.
Se le conoce como “experimento aleatorio” al acontecimiento o fenómeno cuyo resultado no se puede predecir.
Por ejemplo, el experimento de lanzar una pelota a un aro tiene dos posibles eventos, que entre al aro o que no entre. Para este caso se puede determinar como “Evento A” al evento en el que la pelota entra al aro y como “Evento B” al evento en el que la pelota no entre.
Asimismo, se debe comprender el concepto de “espacio muestral”, que se refiere al conjunto de todos los posibles resultados que pueden ocurrir al realizar un experimento aleatorio.
¿Qué hacemos?
¿Conoces las relaciones que se forman entre los eventos? Los hay de dos tipos: eventos que son independientes y los eventos dependientes.
Los eventos independientes son aquellos en donde la probabilidad de ocurrencia de uno no afecta la probabilidad de ocurrencia del otro. Mientras que, en los eventos dependientes, la probabilidad de que ocurra uno de estos eventos impacta directamente en la probabilidad de que ocurra el otro.
Para usar esta definición en la resolución de una situación, se tiene el siguiente ejemplo: si se quiere obtener la probabilidad de que en un grupo de personas se encuentre a una persona que utilice un reloj de pulsera o que le gusten las donas, ¿de qué tipo de eventos se trata?
No afecta en nada que una persona use reloj o que le gusten las donas, por lo tanto, son eventos independientes, ya que la ocurrencia de un evento no depende del otro.
Y para continuar poniendo en práctica se ejemplifica en un problema de aplicación, como se describe en breve:


¿Puedes precisar qué tipo de eventos se tiene para esta situación problemática?
Si se analiza la información, se puede ver que el hecho de que un alumno o alumna se conecte por computadora, o que use audífonos, no afecta la posibilidad de ocurrencia de los eventos entre sí.
Por lo tanto, se identifican dos eventos independientes:
El evento “A” es que un alumno se conecte por computadora.
Y el evento “B” que use audífonos durante la clase.
Y como se trata de eventos independientes se emplea la siguiente fórmula:
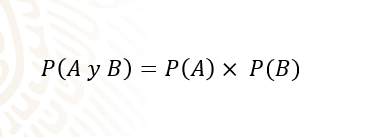
La probabilidad de que ocurran al mismo tiempo, el evento “A” y el evento “B”, es igual al producto de la probabilidad de que ocurra el evento “A”, por la probabilidad de que ocurra el evento B.
Esta es la razón por la que se le conoce como “regla de la multiplicación” o “del producto”.
Para resolver lo anterior, se debe obtener la probabilidad de que ocurra cada uno de los eventos por medio de la fórmula clásica de la probabilidad.
La fórmula clásica de la probabilidad se obtiene dividiendo los eventos favorables entre el total de eventos.
Para el caso del evento “A”, los casos favorables son aquellos alumnos que se conectan utilizando computadora, el problema señala que son 24 de un total de 40 casos posibles.

La operación para obtener la probabilidad del evento “A” es:
Probabilidad del evento “A” es igual a 24 entre 40.
Se reduce a 12 entre 20,
se reduce nuevamente
y es igual a 6 entre 10.
Su representación decimal es igual a 0.6, que equivale a 60 por ciento.
Después, se obtiene la probabilidad del evento “B”, y se utiliza de nueva cuenta la fórmula clásica que, como ya se dijo, consiste en dividir el número de casos favorables entre el total de eventos.
Para la probabilidad del evento “B”, los casos favorables son los 33 alumnos que se conectan usando audífonos. Y se divide entre el total de eventos, que son los 40 alumnos.

De forma tal que la operación es 33 entre 40, que es equivalente a 0.825 y corresponde al 82 por ciento, aproximadamente.
Para calcular la probabilidad en la que ambos eventos ocurran, se realiza la multiplicación de ambas probabilidades:
“tres quintos” por “33 cuarentavos” es igual a 99 entre doscientos.
Si realizas la división obtienes 0.495 y si se multiplican las probabilidades en su equivalente decimal se tiene:
0.6 por 0.825 es igual a 0.495, puedes observar que es el mismo resultado, esto equivale a 49.5 por ciento.
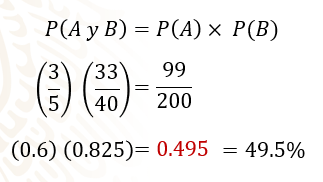
Eso significa que la probabilidad de que al azar se elija a un alumno o alumna que utilice computadora y audífonos al mismo tiempo es de 49.5 por ciento.
Pero ¿qué pasa si se tiene un problema en donde los eventos sean dependientes uno del otro? Es decir, que la probabilidad de ocurrencia de uno dependa o afecte la ocurrencia del otro.
Pasa al siguiente ejemplo para explicar esa situación.

Los antes mencionados son eventos dependientes, ya que la ocurrencia de uno afecta directamente a otro. De este modo, si la primera esfera que sale no se regresa a la caja, afecta al experimento porque ya no son la misma cantidad de esferas, ni la misma cantidad de esferas rojas, azules o blancas, según el color que saliera al inicio.
Como lo refieres, se trata de dos eventos dependientes. Y como no se regresa a la caja la primera esfera extraída, se le llama “sin reemplazo”. De este modo, se analiza el espacio muestral del problema:
Se tiene que la cantidad total de esferas en la urna es de 9. Cuando se ha extraído una bola en el primer evento, se tiene que, para el segundo, al no haber reemplazo en la caja, ya quedan 8 esferas. Por lo tanto, el espacio muestral cambia:
Y la fórmula se interpreta así:
La probabilidad de que ocurra el evento “A” y el evento “B” es igual a multiplicar la probabilidad del evento “A” por la probabilidad de que ocurra el evento “B”, dado que ya ocurrió el evento “A”.
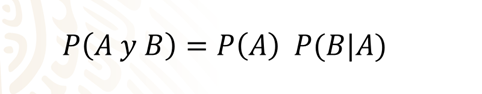
En esta fórmula se toma en cuenta que el evento “A” ya ha ocurrido, a diferencia de lo que ocurre cuando los eventos eran independientes.
¿Qué te parece si se aplica la fórmula a los valores del problema?
En este caso, se obtiene la probabilidad del evento “A”, que es la probabilidad de sacar una esfera amarilla y del evento “B”, que es sacar una esfera azul, para este ejemplo:
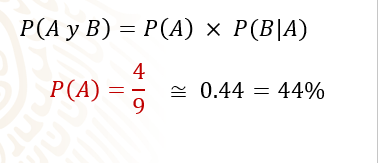
La probabilidad del evento “A” se calcula obteniendo el cociente de 4 entre 9, que tiene por resultado 0.44 o 44 por ciento, aproximadamente.
En el caso de la probabilidad del evento “A”, la división que se realiza es 4 entre 9, ya que 4 son las esferas rojas y en total hay 9 esferas en la urna.
Pero en el caso de que se quiera obtener la probabilidad del evento “B” cuando ocurrió el evento “A”, ya no hay 9 esferas en la urna porque se tomó una de color rojo. Por lo tanto, hay 8 esferas.
De este modo, la división para calcular la probabilidad del evento “B” es de 2 entre 8, que da como resultado 0.25, que se representa como 25 por ciento.

El siguiente paso es multiplicar las dos probabilidades: 0.44 por 0.25 que es 0.11, y que en porcentaje equivale a 11 por ciento.

¿A qué se refiere esta cantidad?
Que la probabilidad de que se saque una esfera roja sin reemplazarla y después una esfera azul es de 0.11 o del 11 por ciento.
- Audiovisual 1
https://youtu.be/2r6Zt32LbHs
(del min. 13.14 al 13.42) - Audiovisual 2
https://youtu.be/2r6Zt32LbHs
(del min.13.45 al 14.07)
En un librero hay 45 videojuegos, de forma tal que hay 10 de acción, 18 de carreras y 17 deportivos.
¿Cuál es la probabilidad de seleccionar al azar un videojuego deportivo y, sin devolver éste, elegir al azar uno de carreras?
Para superar el primer nivel, lo primero debes hacer es obtener la probabilidad de conseguir un videojuego deportivo que, en este caso, es el evento “A”. Esto se obtiene realizando la división 17 entre 45, que es aproximadamente a 0.37.
Mientras que, para obtener la probabilidad del evento “B”, que en este caso es un juego de carreras, se considera la ocurrencia del evento “A”. Por lo tanto, se realiza la división 18 sobre 44, considerando que el experimento es sin reemplazo, se tiene como resultado 0.40, aproximadamente.
Para calcular la probabilidad se tiene que: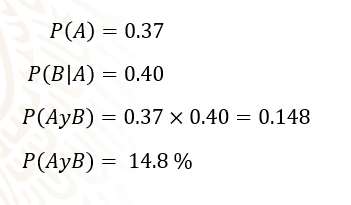
Mientras que, para calcular la probabilidad de obtener ambos eventos se multiplica 0.37 por 0.4 y el resultado es 0.148, que equivale a 14.8 por ciento.
La respuesta correcta resultó ser 14.8 por ciento.
Verifica cómo sigue la transmisión del juego. - Audiovisual 3
https://youtu.be/2r6Zt32LbHs
(del min. 16.09 al 16.34) - Audiovisual 4
https://youtu.be/2r6Zt32LbHs
(del min. 17.58 al 18.18)
El problema al que se enfrenta la jugadora señala lo siguiente:

Para este caso se le llama “Evento A” al evento de seleccionar la caja con las consolas dañadas. Por lo tanto, para obtener la probabilidad del “Evento A” se realiza la división 1 entre 10, pues es sólo una caja en donde se encuentran las consolas dañadas. El resultado es 0.1.
Mientras que para el “Evento B” es extraer una consola dañada, como ya se calculó la probabilidad de extraer la caja con las consolas dañadas. El espacio muestral está definido por la cantidad de consolas en la caja, que son 5.
Entonces, la probabilidad del “Evento B” es 3 entre 5, y el resultado de esta operación es 0.6.
De este modo, la probabilidad de seleccionar una consola dañada en la primera caja que se abra es de 0.06 o 6 por ciento de probabilidad. - Audiovisual 5
https://youtu.be/2r6Zt32LbHs
(del min. 17.59 al 18.18)
El problema para completar el nivel dice así:
Para el tercer problema, la cantidad total de videos que se encuentran en el canal es de 96, de los cuales 45 videos son de Historia.
Entonces, se tiene que el “Evento A” es la reproducción aleatoria de un video de Historia: la probabilidad del evento “A” es igual a 45 entre 96, y da como resultado aproximado 0.46.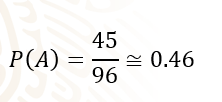
Y el “Evento B” es el caso en el que el siguiente video en reproducirse sea de Matemáticas, dado que ya se reprodujo uno de Historia.
Por lo tanto, se tienen 35 videos de Matemáticas, pero ahora están a disposición 95 videos, porque uno ya se eliminó de la lista de reproducción.
De este modo, la probabilidad del “Evento B” se obtiene al dividir 35 entre 95, dejando como resultado aproximado 0.36.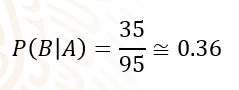
Después, para la probabilidad de ocurrencia de ambos eventos, se calcula el producto de ambas probabilidades:
P (A y B) es igual a la probabilidad del evento “A” por la probabilidad de que ocurra el evento “B”, dado que ya ocurrió el evento “A”.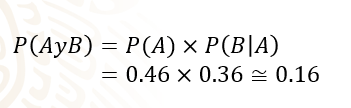
Esto es igual a 0.46 por 0.36, igual a un resultado aproximado de 0.16 o 16 por ciento. - Audiovisual 6
(del min. 20.29 al 20.42)
La jugadora superó los 3 niveles en una sola partida. No hay duda de que las alumnas y los alumnos de secundaria son muy hábiles.
Y, además, resolvió los problemas que se le presentaron con la regla del producto.
Pero revisa un último problema:

¿Qué se considera primero?
Saber si los eventos que estás analizando son dependientes o independientes y para este caso son eventos dependientes, ya que la ocurrencia del primero de ellos afecta a la ocurrencia del otro.
En este problema se tienen los datos en porcentaje. Se sabe la probabilidad de ocurrencia del evento “A”, de los pares de calcetines oscuros equivalen al 64 por ciento.
Como has visto en casos anteriores, si el evento “A2 ya ha ocurrido, entonces en vez de considerar 50 pares de calcetines debes considerar 49, por lo que el porcentaje de calcetines blancos que es de 16 por ciento parece ser poco útil por el momento.
Pero ¿cómo supiste que el porcentaje de calcetines blancos era de 16 por ciento?
El razonamiento fue el siguiente: si el 20 por ciento son estampados y el 64 por ciento son oscuros, eso nos da 84 por ciento y lo que falta para el 100 por ciento es el 16 por ciento.
Averigua entonces, cuántos pares de calcetines corresponden al 16 por ciento.
Calcula mediante una proporción este dato.
Ese concepto se refiere a una relación de igualdad que existe entre dos razones.
Utilizarás una de las propiedades de las proporciones para resolver este problema.
Estableces la proporción, que en este caso será que 50 pares de calcetines es igual al 100 por ciento, por lo que 16 por ciento debe ser igual a equis pares de calcetines.
“x” es igual a 16 por 50 entre 100.
Que es igual a 800 entre 100 igual a 8.

Y de esta forma obtienes el resultado que es ocho, por lo que 16 por ciento de los calcetines es equivalente a 8 pares.
Ahora con ese dato puedes utilizar la fórmula que estudiaste en la sesión, es decir, la regla del producto, considerando que al obtener el primer par de calcetines de color oscuro ahora quedan 49 pares.
Se tiene:
Sea “A” obtener un par de color oscuro.
Sea “B” obtener un par blanco.
Probabilidad del evento “A” es igual al 64 por ciento.
Probabilidad del evento “B” es igual a 8 entre 49.
Que es aproximadamente 0.163, que equivale al 16.3 por ciento.
Se aplica la regla del producto y se tiene 64 por ciento por el 16.3 por ciento.
Lo cual da como resultado el 10.4 por ciento, aproximadamente.
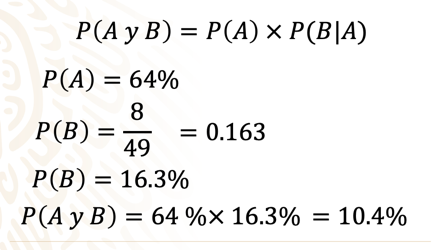
Siendo este el resultado final.
En resumen: Primero, se resolvieron distintos problemas utilizando la “regla del producto”. Con esta, se obtuvo la probabilidad de que ocurra un “evento A” y un “evento B”, tanto para eventos independientes como dependientes.
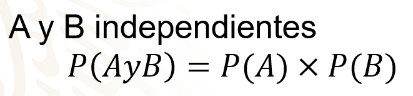
Cuando se trata de eventos independientes, se utiliza la siguiente fórmula:
Probabilidad de que ocurra “A” y “B” es igual a la probabilidad del evento “A”, por la probabilidad del evento “B”.

En caso de eventos dependientes se utiliza: probabilidad de que ocurra “A” y “B” es igual a la probabilidad de “A”, por la probabilidad del evento “B” en cuanto ha ocurrido el evento “A”.
El reto de hoy:
Encuentra a tu alrededor situaciones en que aplique la probabilidad de ocurrencia de dos eventos.
Busca más problemas en tus libros de texto para consolidar tu aprendizaje.
¡Buen trabajo!
Gracias por tu esfuerzo.
