Razones trigonométricas I
Razones trigonométricas I
Aprendizaje esperado: resuelve problemas que implican el uso de las razones trigonométricas seno, coseno y tangente.
Énfasis: dar sentido y significado a las razones trigonométricas.
¿Qué vamos a aprender?
En esta sesión aprenderás a identificar las razones obtenidas a partir de los lados de un triángulo rectángulo, al tomar como referencia uno de sus ángulos agudos.
Para medir una longitud o una distancia, se toma una unidad, por ejemplo, el metro.
Se coloca el instrumento de medición sobre la distancia a calcular para ver cuántas veces cabe.
Sin embargo, esto no es posible en algunos planteamientos, por ejemplo, para medir la distancia de la Tierra a la Luna, el diámetro de la Tierra, la altura de una montaña o la anchura de un lago.
Para medir distancias inaccesibles como las anteriores se utiliza la trigonometría.
La trigonometría es una rama de las matemáticas que estudia la relación entre los lados y los ángulos de los triángulos, en particular, los triángulos rectángulos.

Sin embargo, y como ocurre con frecuencia en las matemáticas, la trigonometría no es creación de un solo individuo o nación. Los resultados sobre las relaciones entre los lados de triángulos semejantes fueron conocidos y utilizados en el antiguo Egipto y en Babilonia.
Durante mucho tiempo el desarrollo de la trigonometría estuvo asociado a la astronomía y no fue una disciplina que sólo los matemáticos árabes practicaron, quienes la preferían sobre cualquier otra parte de las matemáticas, excepto, quizás, el álgebra.
Fue hasta el siglo XV que el matemático del Renacimiento Johann Müller publicó dos textos sobre la trigonometría.

El primero fue un resumen del “Almagesto de Ptolomeo”, el más grande tratado de astronomía, escrito durante el segundo siglo de nuestra era.
El segundo fue un estudio detallado de los diferentes métodos para resolver triángulos arbitrarios.
Estos dos textos pautan el nacimiento de la trigonometría como una parte de las matemáticas independiente de la astronomía.
Conocer la historia de la trigonometría es un recurso para entender el origen de los conceptos aquí planteados.
La sesión se divide en 3 partes:
- Primero se identifica qué es un triángulo rectángulo y cómo se nombran sus lados respecto a sus ángulos.
- Después se presentan las relaciones entre dos longitudes de los lados de un triángulo rectángulo, con respecto a uno de sus ángulos agudos.
- Y al final, una actividad para poner a prueba los conocimientos adquiridos durante la sesión.
¿Qué hacemos?
Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90°.
Los otros dos ángulos son agudos, y si no se conocen sus medidas, se puede utilizar la nomenclatura para nombrarlos. Se sabe que, frecuentemente para las nomenclaturas, se utilizan letras minúsculas del alfabeto griego. En el ejemplo se utilizan alfa y beta.
En el triángulo rectángulo se le denomina “hipotenusa” al lado opuesto del ángulo recto. Si observas, su longitud es la mayor de los tres lados.
Por otra parte, se le llama cateto a cada uno de los lados que forman el ángulo recto.
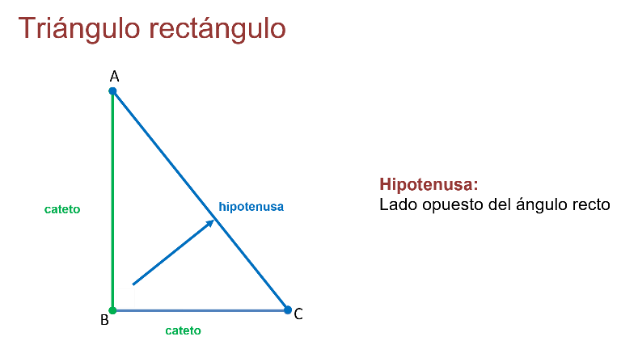
El cateto opuesto de un ángulo es el lado que no forma parte de dicho ángulo, es decir, el lado que está frente al ángulo.
Y el cateto adyacente de un ángulo es el lado que forma parte de dicho ángulo.
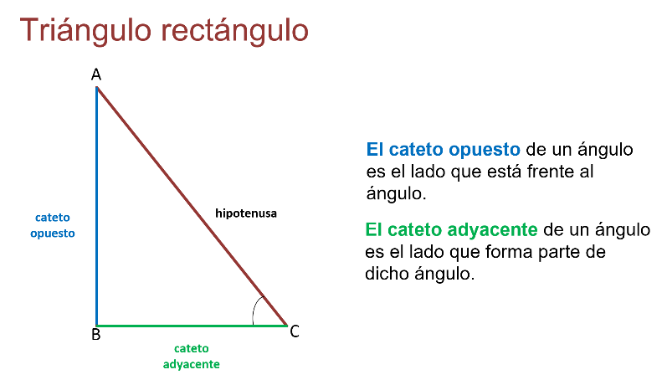
Observa el siguiente ejemplo para aplicar lo anterior.
En el triángulo ABC, la hipotenusa es el lado BC por ser el lado opuesto al ángulo recto.
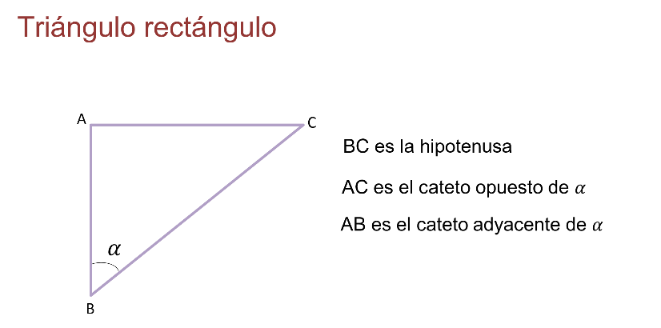
Si se quiere saber cuál es el cateto opuesto del ángulo alfa, basta con observar el lado que no forma parte del ángulo, es decir, el lado AC. Observa cómo AC está frente al ángulo alfa.
Por lo tanto, el cateto adyacente es el lado AB, y se reconoce porque es un lado que forma parte de ese ángulo sin ser la hipotenusa.
En el mismo triángulo, si se toma como referencia el ángulo beta, la hipotenusa sigue siendo el lado BC, al ser el lado opuesto al ángulo de 90°.
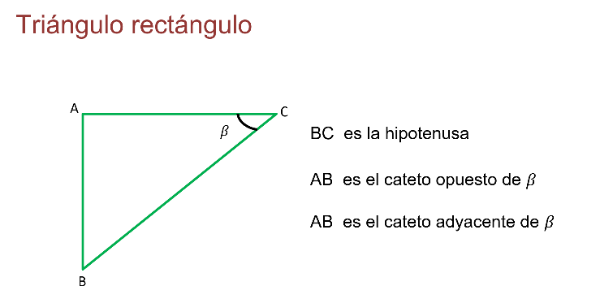
Si se quiere saber cuál es el cateto opuesto del ángulo beta, se observa el lado que no forma parte del ángulo beta. Este es el lado AB, porque el lado AB está frente al ángulo beta.
El cateto adyacente del ángulo beta es el lado AC, al formar parte de este ángulo.
El nombre que reciben los lados de un triángulo rectángulo son cateto opuesto y cateto adyacente; depende del ángulo al que se hace referencia.
En el caso de la hipotenusa, ésta siempre será el lado opuesto al ángulo de 90°.
Ya sabes cómo identificar la hipotenusa, el cateto opuesto y el cateto adyacente de un triángulo rectángulo. Resuelve la siguiente actividad.
En los siguientes triángulos, ¿cuál es la hipotenusa?

Se debe analizar cada triángulo y sus características. ¿Son todos triángulos rectángulos?
En el primer triángulo se observa el lado opuesto al ángulo de 90°, el cual mide 15 cm. Por lo tanto, este lado es la hipotenusa.
En el segundo triángulo, la hipotenusa es el lado que mide 8.5 cm, al ser el lado opuesto al ángulo de 90°.
En el tercer triángulo no es posible determinar la hipotenusa al no ser un triángulo rectángulo.
Identifica el cateto opuesto del ángulo alfa y del ángulo de 35°, respectivamente.
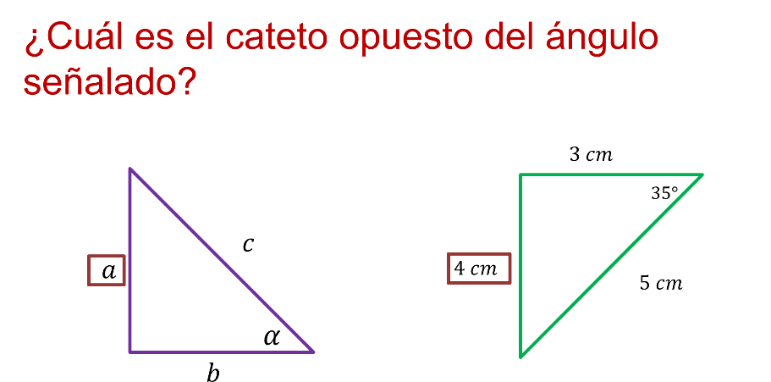
En el primer triángulo, el ángulo marcado es alfa. Para identificar el cateto opuesto, se identifica el lado que no pertenece al ángulo, o bien el lado frente a él.
¿Cuál lado es?, ¿lado “a”, “b” o “c”?
Si contestaste “lado a”, estás en lo correcto. El lado “a” es el cateto opuesto del ángulo alfa.
En el segundo triángulo, ¿cuál es el cateto opuesto del ángulo de 35°? Si respondiste que es el lado de 4 cm, al estar opuesto al ángulo de 35°, estás en lo correcto.
El siguiente ejemplo, un nuevo desafío: identifica cuál es la hipotenusa, el cateto opuesto y el cateto adyacente de los siguientes triángulos.
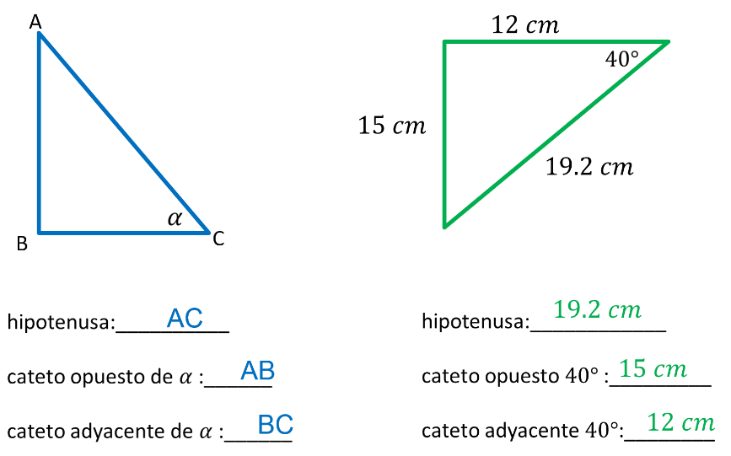
Hay dos triángulos: en el primero está marcado el ángulo alfa, y en el segundo, un ángulo de 40°.
En ambos triángulos se quiere identificar la hipotenusa, el cateto opuesto y el cateto adyacente.
Del primer triángulo ABC, la hipotenusa es el lado AC, al ser el lado opuesto al ángulo de 90°.
El cateto opuesto al ángulo alfa es el lado AB, al no pertenecer a los lados del ángulo alfa y estar frente al ángulo alfa.
El cateto adyacente al ángulo alfa es el lado BC.
En el segundo triángulo, la hipotenusa es el lado de medida 19.2 cm, al estar opuesto al ángulo.
El cateto opuesto del ángulo de 40° es el lado de 15 cm, y el cateto adyacente es el lado de 12 cm.
Relaciona las medidas de dos de los lados de un triángulo rectángulo con respecto a uno de sus ángulos agudos.
Observa qué sucede al variar la longitud de uno de los catetos de un triángulo rectángulo.
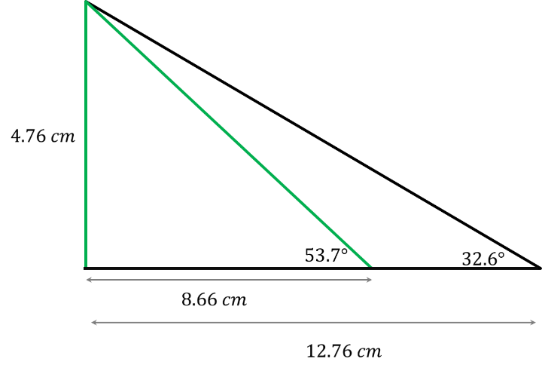
Como se observa, cambia la longitud de la hipotenusa.
Si se fija el valor de dos longitudes o de una longitud y un ángulo agudo, entonces existe un único triángulo rectángulo.
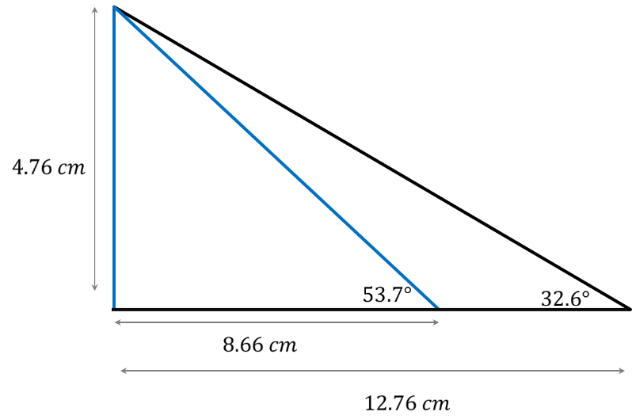
En este caso, se tienen dos longitudes: las que corresponden a los catetos. Se calcula entonces la tercera longitud con el teorema de Pitágoras.
Pero si se tiene la longitud de un cateto o de la hipotenusa, y la medida de un ángulo agudo del triángulo rectángulo, se necesita una herramienta para averiguar las longitudes desconocidas.
Estas herramientas reciben el nombre de “razones trigonométricas”. Se les llaman “razones” porque establecen una relación en forma de cociente entre dos longitudes. Y son “trigonométricas” porque estas longitudes pertenecen a los lados de un triángulo.
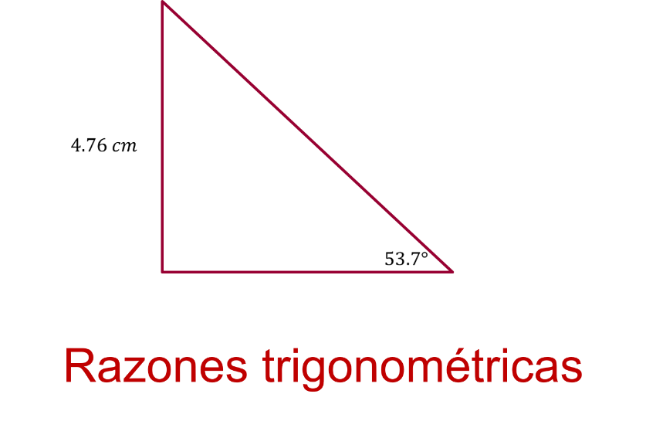
Para encontrar las razones trigonométricas, se deben relacionar las medidas de dos de los lados de un triángulo rectángulo, con respecto a uno de sus ángulos agudos.
Por ejemplo, se relacionan las medidas de dos de los lados del triángulo rectángulo ABC con respecto al ángulo alfa.
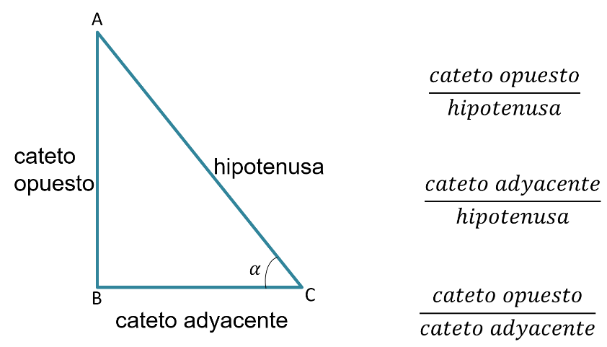
Se tiene el cateto opuesto sobre hipotenusa y el cateto adyacente sobre hipotenusa.
Pero ¿existe otra relación de las medidas de dos de los lados del triángulo con respecto al ángulo?
El cateto opuesto sobre cateto adyacente.
Entonces es posible obtener tres razones al relacionar las medidas de dos de los lados de un triángulo rectángulo con respecto a un ángulo.
A las razones se les conoce como razones trigonométricas.
Dado el ángulo alfa, al cociente de la longitud del cateto opuesto entre la hipotenusa se le conoce como seno, y se expresa con la palabra “sen”.
Dado el ángulo alfa, al cociente de la longitud del cateto adyacente entre la hipotenusa se le conoce como coseno y se representa con la palabra “cos”.
Dado el ángulo alfa, al cociente de la longitud del cateto opuesto entre el cateto adyacente se le conoce como tangente y se denota con la palabra “tan”.
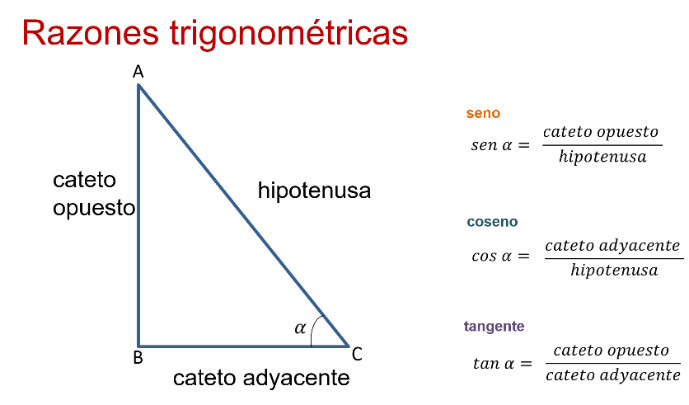
Las razones trigonométricas son seno, coseno y tangente, y su uso permite resolver diversas situaciones. Analiza una de ellas.
Identifica las razones trigonométricas. Toma como referencia el ángulo beta.
La razón trigonométrica “seno” es igual al cateto opuesto sobre hipotenusa.
Al identificar el ángulo beta en el triángulo, se tiene al lado BC como el cateto opuesto, y el lado AC como la hipotenusa.
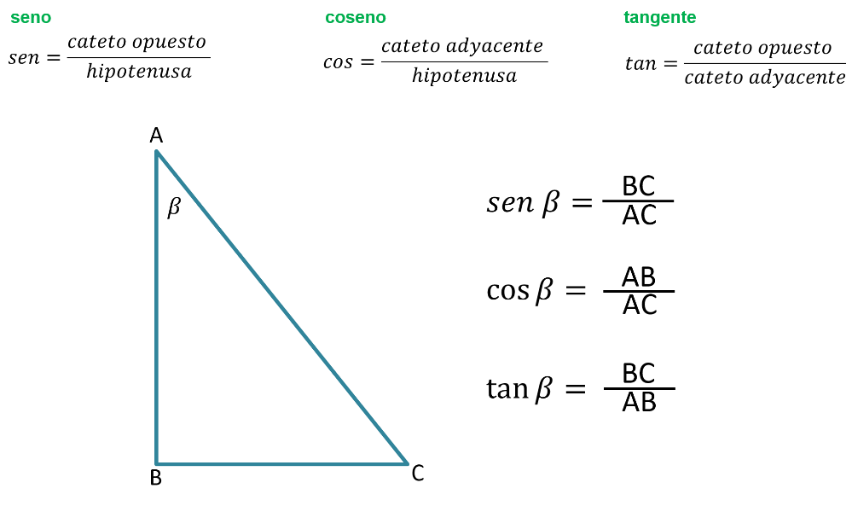
Por lo tanto, el “seno de beta” es igual a BC sobre AC.
Se continúa con el coseno igual al cateto adyacente sobre hipotenusa.
Al identificar el ángulo beta en el triángulo, se tiene el lado AB como cateto adyacente, y el lado AC como la hipotenusa.
Por lo tanto, el “coseno de beta” es igual a AB sobre AC.
Al final, la tangente es igual al cateto opuesto sobre cateto adyacente.
El lado BC es el cateto opuesto al ángulo beta, el lado AB es el cateto adyacente y la “tangente de beta” es igual a BC sobre AB.
Tres razones trigonométricas fundamentales son: seno, coseno y tangente.
Pero ¿qué otros cocientes se obtienen a partir de las medidas de los lados de un triángulo rectángulo?
Existen las razones trigonométricas inversas cosecante, secante y cotangente.
- Cosecante es la razón inversa del seno.
- Secante es la razón inversa del coseno.
- Cotangente es la razón inversa de la tangente.

Es importante saber que existen las razones trigonométricas inversas; sin embargo, a lo largo de las siguientes sesiones te enfocaras únicamente en trabajar con las razones seno, coseno y tangente.
¿Alguna vez has intentado calcular alguna distancia inaccesible, como la altura de un árbol, la de una casa de dos pisos o el ancho de un río?
Las situaciones anteriores ilustran cómo se procede usando trigonometría.
Las diversas situaciones se traducen en problemas de triángulos y se resuelven al utilizar las razones trigonométricas; es decir, las relaciones entre los lados y los ángulos de un triángulo.
Resolver un triángulo significa:
- Dados los tres lados, encontrar los ángulos.
- Dados dos lados y el ángulo comprendido entre ellos, encontrar el tercer lado y los otros dos ángulos.
- Dados un lado y los ángulos adyacentes, encontrar los otros dos lados y el ángulo faltante.
Las razones trigonométricas sirven para resolver problemas donde se requiera encontrar los lados o ángulos de un triángulo rectángulo.
Recapitula lo aprendido con Juan Palomo, quien, desde la costa del Pacífico mexicano, explica la anatomía de su aleta en triángulo rectángulo.
- Juan Palomo – Triángulos
https://youtu.be/E9XBTZZ14bg?t=1203
Del minuto 20:03 a 21:40
Se conocen como razones trigonométricas a las obtenidas a partir de la razón entre los lados de un triángulo rectángulo y, como referencia, uno de sus ángulos agudos.
Las tres razones trigonométricas fundamentales son seno, coseno y tangente:
- Al cociente de la longitud del cateto opuesto entre la hipotenusa se le conoce como seno y se denota con la palabra “sen”.
- Al cociente de la longitud del cateto adyacente entre la hipotenusa se le conoce como coseno y se denota con la palabra “cos”.
- Al cociente de la longitud del cateto opuesto entre el cateto adyacente se le conoce como tangente y se denota con la palabra “tan”.
Las razones trigonométricas sirven para resolver situaciones que se traducen en problemas de triángulos, es decir, para encontrar los lados o ángulos de un triángulo rectángulo.
La siguiente actividad pone a prueba tus conocimientos adquiridos durante esta sesión.
Anota las respuestas en el cuaderno para verificar los resultados al final.
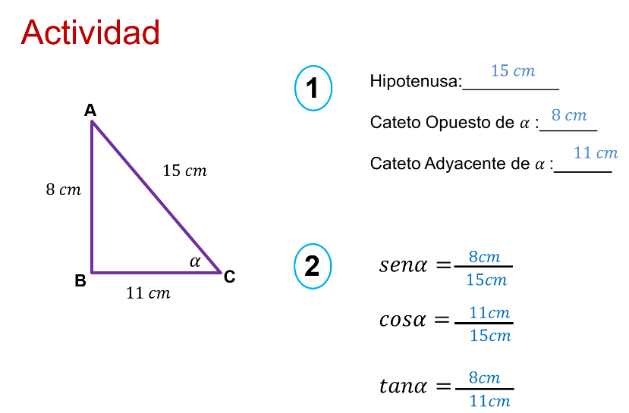
La actividad consta de 2 partes.
La primera parte, con base en el triángulo rectángulo, se debe ubicar la hipotenusa, el cateto opuesto del ángulo alfa y el cateto adyacente del ángulo alfa.
La segunda parte es identificar del mismo triángulo las razones seno, coseno y tangente con respecto al ángulo alfa.
Las respuestas de la primera parte son:
- La hipotenusa es el lado de 15 cm, el cateto opuesto al ángulo alfa es de 8 cm y el cateto adyacente al ángulo alfa es de 11 cm.
Las respuestas de la segunda parte son: - Seno de alfa es igual a 8 cm sobre 15 cm, coseno de alfa es igual a 11 cm sobre 15 cm y tangente de alfa es igual a 8 cm sobre 11 cm.
Si tienes dudas o quieres ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
El reto de hoy:
Se tiene la medida de un lado y un ángulo agudo en un triángulo rectángulo. Con esta información se pueden obtener las medidas de los otros lados.
Se quiere calcular la altura del árbol. ¿Qué razón trigonométrica utilizarías: seno, coseno o tangente para saber la altura del árbol?
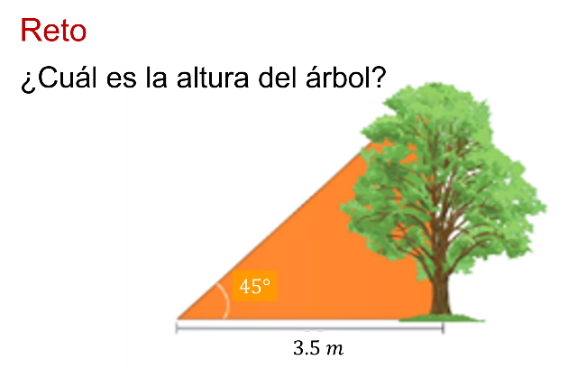
Una vez seleccionada la razón trigonométrica, ¿qué operaciones se realizan?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas