Razones de cambio entre dos conjuntos de cantidades
Razones de cambio entre dos conjuntos de cantidades
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: encontrar las razones de cambio de dos conjuntos de cantidades que están en una relación de proporcionalidad directa.
¿Qué vamos a aprender?
Es importante que realices las actividades y notas en tu cuaderno sobre lo aprendido, así como tus dudas en torno a la sesión.
Lo que vas a necesitar es tu cuaderno, regla, lápiz o bolígrafo y lápices de colores.
Un estudiante de la Secundaria #23 para Trabajadores platicó lo útil que le son las matemáticas. Por ejemplo, su familia se dedica a vender botellones con agua, y la cantidad de ganancia recibida en pesos al final del día es directamente proporcional al número de botellones que vende.
Pero ¿qué significa que dos cantidades sean directamente proporcionales?
Examina lo que es una relación de proporcionalidad directa, que es con lo que iniciarás.
¿Qué hacemos?
Analiza la siguiente situación. Aída de 6 años y Samuel de 12 años, con una diferencia de edades entre ellos de 6 años.
Ellos se preguntan si sus edades están relacionadas proporcionalmente.
A continuación, observa en la tabla algunos datos relacionados con las edades de estos estudiantes.
En la tabla se han colocado las edades de Aída y Samuel a lo largo de varios años:
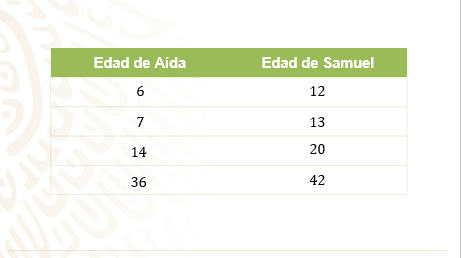
Es verdadera o falsa cada una de las siguientes afirmaciones:
¿La edad de Samuel es igual a la edad de Aída multiplicada por 2 en cualquier año?
Con el primer dato, si Aída tiene 6 años, entonces 6 por 2 es igual a doce. Esta afirmación es verdadera porque la edad de Aída y la de Samuel son iguales.
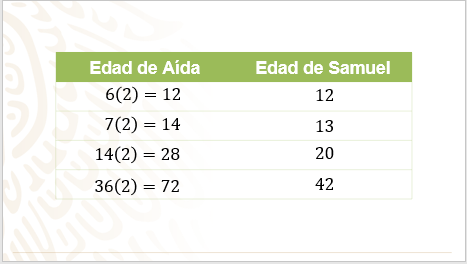
En el segundo resultado, las edades no coinciden. Porque 7 por 2 son 14, y Samuel en ese año tendría sólo 13 años.
Y en el tercer resultado, sucede algo similar, no corresponden las edades. Aída con 14 años por 2 es igual a 28 años, y Samuel tendrá 20 años.
Del mismo modo, cuando Aída tenga 36 años por 2 son 72 años, y Samuel apenas tendrá 42 años.
En conclusión, la edad de Aída multiplicada por dos para cualquier año no corresponde a la edad de Samuel. Los valores asociados a las edades no están relacionados a través de la proporcionalidad directa.

En la tabla se observa que la edad de Samuel es siempre igual a la edad de Aída más seis.
Es decir, todos los valores de la segunda columna se pueden obtener sumando 6 a los valores de la primera.
Esto se puede expresar con una regla de correspondencia: la edad de Samuel es igual a la edad de Aída más 6, o bien, si se usan letras: “s” es igual a “a” más 6
Por lo tanto, la tabla muestra una relación entre dos conjuntos de cantidades, más no son una relación proporcional directa.
Si analizas el ejemplo de la Secundaria #23: se sabe que cada botellón o garrafón con agua cuesta 40 pesos y por cada botellón vendido su familia gana 8 pesos. Pero ¿cuánto gana si hoy vende 10 botellones con agua?
Si por cada botellón gana 8 pesos y vende 10 botellones, 8 por 10 es igual a 80. Entonces, ganaría 80 pesos.
Piense en que mañana será un muy buen día y venderá 20 botellones con agua, es decir, el doble de hoy. ¿Cuánto será su ganancia?
Si se multiplica 8 por 20 igual a 160 pesos; ganaría exactamente el doble.
En conclusión, la cantidad de botellones vendidos es directamente proporcional a la ganancia recibida.
Porque si la cantidad de un conjunto aumenta dos veces, tres veces o “n” cantidad de veces, y la cantidad correspondiente a otro conjunto aumenta el mismo número de veces, se dice que las cantidades de ambos conjuntos son directamente proporcionales.
Para comprender mejor este concepto observa el siguiente video del inicio al minuto 02:12
- Gráficas, tablas y expresiones algebraicas
Cuando dos conjuntos de cantidades están relacionados entre sí, se puede estudiar el cambio o incremento de una cantidad con respecto al cambio o incremento de la otra.
Al cociente que se obtiene de dividir el incremento de una cantidad, entre el incremento correspondiente a la otra, se le llama razón de cambio.
Es decir, la razón de cambio en el caso de los botellones de agua es que, por 1 botellón se tienen 8 pesos de ganancia.
¿En qué otros casos se emplea la razón de cambio entre dos cantidades directamente proporcionales?
Por ejemplo, en las tarifas y el costo de las llamadas por teléfono.
Una compañía decidió no cobrar renta mensual y sólo cobrar por las llamadas realizadas.
Ángel, que vive con sus padres y tres hermanos, contrató el servicio telefónico durante el mes de diciembre. En ese mes, cada miembro de la familia hizo una llamada telefónica y anotó el costo y la duración.
En una ocasión, anotaron el costo de 15 pesos de una llamada con duración de 5 minutos, ¿cuánto costó cada minuto de esa llamada?
La llamada costó 15 pesos y duró 5 minutos. Se realiza una división, 15 entre 5 igual a 3. Cada minuto costó 3 pesos
En la tabla descrita a continuación se colocan los datos conocidos: la llamada de 5 minutos y su costo de 15 pesos; la llamada de 1 minuto y su costo de 3 pesos.
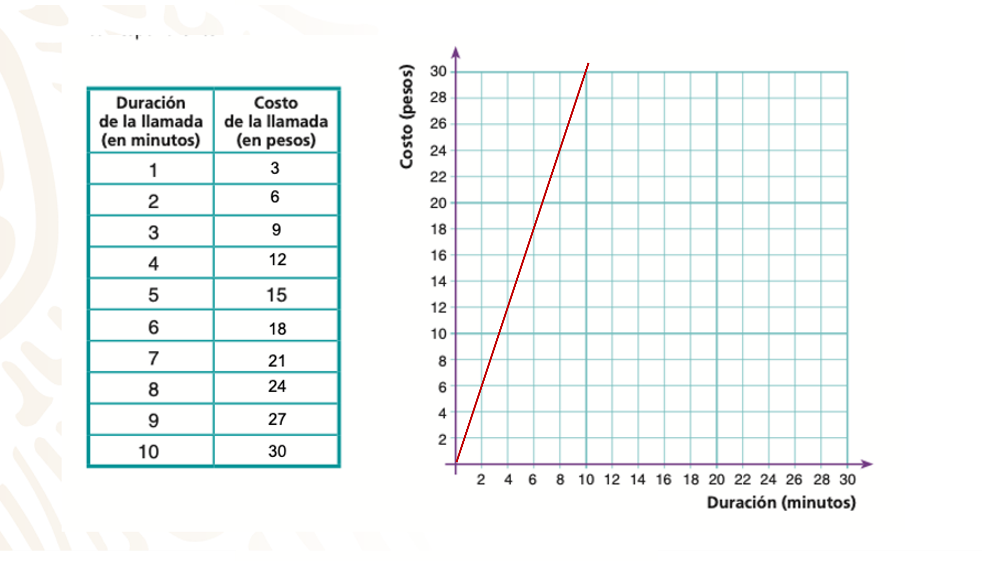
Coloca los valores faltantes en la tabla y realiza la gráfica correspondiente a los datos.
Al observar la gráfica, ¿consideras que las cantidades que representan el costo de las llamadas por minuto están en proporción directa?
Son proporcionales porque al aumentar el tiempo de la llamada, por ejemplo, al doble o al triple, también aumenta su costo al doble o al triple, según corresponda.
Por otra parte, observa que la gráfica de las dos cantidades en proporción directa es una colección de puntos sobre una línea recta que pasa por el origen.
La razón de cambio entre dos cantidades es el cociente del incremento de una cantidad entre el incremento correspondiente a la otra cantidad. ¿Cuál es la razón de cambio sobre la duración de las llamadas y su costo?
La razón de cambio se obtiene de la duración de las llamadas con respecto a su costo, es decir: 5 minutos es a 15 pesos.
Se sabe que las razones de cambio no representan cantidades que se operen entre sí, sino sólo es la comparación entre ellas.
Por lo tanto, ocupando el máximo común divisor de ambas cantidades, que es 5, se simplifica y queda:
5 minutos es a 15 pesos, igual que 1 minuto es a 3 pesos.
La razón de cambio es: por cada minuto el costo es de 3 pesos. Lo cual coincide con los datos obtenidos en la tabla anterior.
Una segunda situación es sobre la relación entre la distancia recorrida y la cantidad de gasolina consumida por tres automóviles.
Recuerda que el rendimiento de gasolina de un automóvil es la cantidad de kilómetros que recorre con un litro de gasolina.
Un auto rinde 18 kilómetros por litro de gasolina.
Y si el rendimiento del auto es constante, la distancia recorrida y la cantidad de gasolina que se consume son cantidades.
Directamente proporcionales.
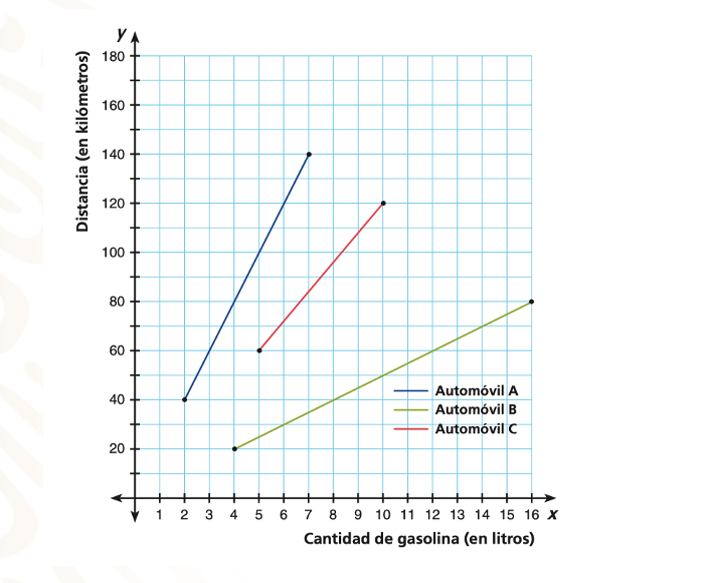
De acuerdo con la información de la gráfica, ¿cuál de los tres automóviles tiene mayor rendimiento?
En las gráficas se observa que el automóvil “A” tiene un mayor rendimiento a diferencia del automóvil “C”, que es el de menor rendimiento.
Analiza la siguiente tabla para comprobar la respuesta.
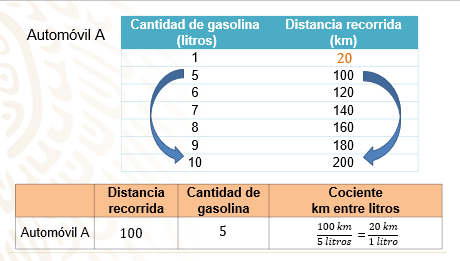
En ella se muestra la relación de la distancia recorrida por el automóvil “A” a partir de la cantidad de gasolina consumida con base en los datos de la gráfica.
¿Cuál es la diferencia de kilómetros recorrida por el automóvil “A” de 5 a 10 litros de gasolina?
Son 100 km.
¿Y cuál es la diferencia de litros que se consumen entre 100 a 200 km?
Son 5 litros.
Se tiene la razón de cambio: 100 km recorridos es a 5 litros.
¿Cuál es la razón de cambio para un litro de gasolina?
Se simplifica, 100 km recorridos es a 5 litros como 20 km es a 1 litro.
¿Y cuál es la razón de cambio entre los litros de gasolina consumidos y la cantidad de kilómetros recorridos para el automóvil “C”?
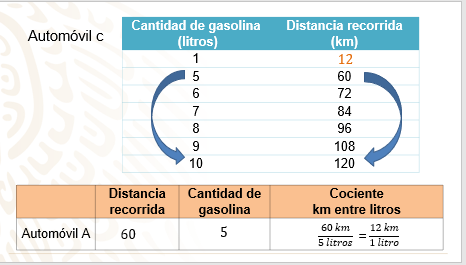
Para el automóvil “C” la diferencia de kilómetros recorridos de 5 a 10 litros son 60 km.
Y la diferencia en litros consumidos es de 5
La razón de cambio es: 60 km es a 5 litros.
Al simplificar se tiene que 12 km es a 1 litro, es decir, por cada litro de gasolina el automóvil “C” rinde 12 km.
Coloca los datos en la tabla, considerando las distancias recorridas del quinto litro al séptimo litro de gasolina consumida para ambos automóviles.
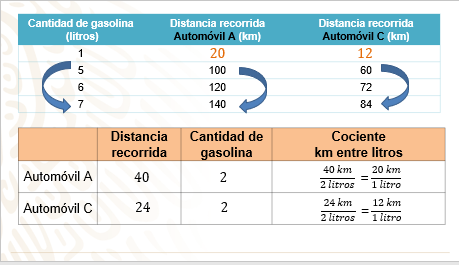
Para el automóvil “A”: la diferencia entre los km recorridos es de 40 km, con una diferencia de 2 litros de gasolina.
La razón de cambio es 40 km es a 2 litros; al simplificar, por cada litro de gasolina se obtienen 20 km recorridos.
Y para el automóvil “C”, la diferencia es de 24 km con una diferencia de 2 litros de gasolina.
La razón de cambio es: 24 km es a 2 litros, es decir, por cada 12 km recorridos se gasta 1 litro de gasolina.
Pero las razones de cambio encontradas en las dos tablas para el automóvil “A”, son iguales.
Y, las razones de cambio para el automóvil “C”, también son iguales
¿Qué automóvil tuvo un mejor rendimiento?
El automóvil “A”, que rinde 20 kilómetros por litro.
Para el automóvil “B”, ¿cuál es la razón de cambio entre la distancia recorrida y los litros de gasolina consumidos?
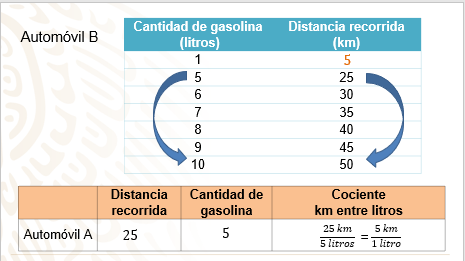
La diferencia entre los kilómetros es de 25 km con una diferencia de 5 litros.
La razón de cambio es: 25 km es a 5 litros de gasolina; por lo tanto, por cada litro de gasolina se recorren 5 km.
Y ahora, de los tres automóviles, ¿cuál tiene un mayor rendimiento?
El automóvil “A” rinde 20 km por litro; el automóvil “B” rinde 5 km por litro, y el automóvil “C” rinde 12 km por litro.
En definitiva, el automóvil “A” tiene mayor rendimiento al dar 20 km por litro de gasolina.
Tal como se interpretó en la gráfica al inicio de la sesión.
Recapitula lo aprendido hasta aquí.
Cuando dos conjuntos de cantidades están relacionados entre sí, se puede estudiar el cambio o incremento de una cantidad respecto al cambio o incremento de la otra.
Por ejemplo, la distancia recorrida está relacionada de manera directamente proporcional a la cantidad de gasolina consumida. Los incrementos de esas cantidades se pueden comparar a través de una razón.
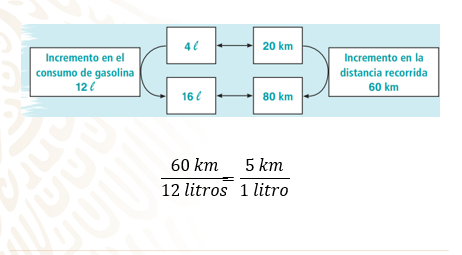
Por ejemplo: si el incremento en el consumo de gasolina son 12 litros, y el incremento de la distancia recorrida son 60 km, el cociente que se obtiene con el incremento de una cantidad entre el incremento correspondiente a la otra se le llama “razón de cambio”.
En este caso, la razón de cambio es: 60 kilómetros es a 12 litros, es decir, el rendimiento del automóvil son 5 kilómetros por litro de gasolina.
Un ejemplo más
¿Sabes cuál es el costo del viaje por persona en el metro de la Ciudad de México?
El costo del viaje por persona es de cinco pesos.
Es decir, la razón de cambio del costo por viaje es 5 pesos por persona.
¿Cuánto pagará una familia de cuatro personas por un viaje?
Si la razón de cambio es de 5 pesos por persona, son veinte pesos
¿Y cuánto pagarás si compran los boletos de ida y vuelta?
40 pesos.
¿Y cuántas personas viajaron si se pagaron 30 pesos por un solo viaje?
6 personas
Los siguientes datos del número de viajes y el monto pagado en cada caso. También observa la gráfica.
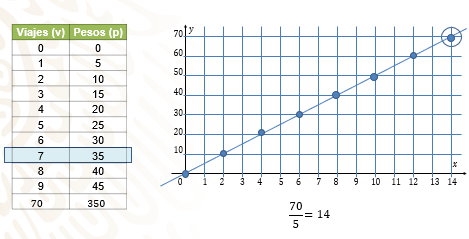
Si se gastaron 35 pesos, ¿cuántos viajes se compraron?
Siete viajes.
Ahora, ¿cuál será la máxima cantidad de viajes que se pueden comprar con 70 pesos?
70 pesos, 14 viajes.
¿Cómo se obtuvo ese resultado?
Como cada viaje cuesta 5 pesos, que es la razón de cambio, entonces dividí 70 entre 5 y obtuve el número de viajes posibles y son 14
Observa la gráfica y al ubicar 14 viajes con 70 pesos, el punto pertenece a la gráfica, lo cual indica que los valores son correctos.
Ahora, obtén el cociente: 350 pesos entre 70 viajes y de cada uno de los renglones de la tabla.
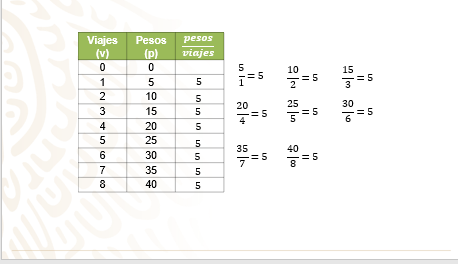
Como podrás darte cuenta, existe una relación proporcional entre las variables: número de viajes y costo en pesos.
Al realizar los cocientes se obtiene la razón de cambio igual a 5 pesos.
Así, la cantidad a pagar aumenta 5 pesos por cada viaje.
Se demostró que una relación de proporción directa es lineal; sin embargo, no todas las relaciones lineales son proporcionales.
Aprendiste que las razones de cambio de dos conjuntos de cantidades que están en una relación de proporcionalidad directa.
El reto de hoy:
Resuelve dudas y ejercita lo aprendido, apóyate de tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.