Proporcionalidad inversa y su expresión general
Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.
Énfasis: diferenciar el tipo de proporcionalidad (directa e inversa) que representa una situación a partir de la forma en que varía, y reconocer la expresión general de una relación de proporcionalidad inversa.
¿Qué vamos a aprender?
Reconocerás cómo diferenciar los tipos de proporcionalidad, directa o inversa que representa una situación, a partir de cómo se relacionan las variables a través del registro de datos en tablas. Profundizarás en la relación de proporcionalidad inversa.
Además, analizarás y resolverás algunos problemas de proporcionalidad directa para diferenciarla de la proporcionalidad inversa.
¿Qué hacemos?
Para comenzar con la sesión, revisa el siguiente planteamiento:
Ejercicio 1. Los limones.
En un negocio de jugos quieren saber, ¿cuánto deben pagar por 1, 2, 3, 4, y 5 kilogramos de limones?
Observa la siguiente tabla, en la cual se registra el precio que se pagaría por 1, 2, 3, 4, y 5 kg de limones.
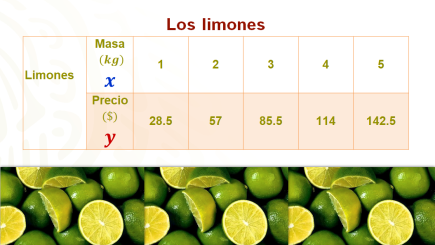
Ahora, responde la siguiente pregunta:
¿Qué tipo de proporcionalidad observas entre los datos de la tabla? ¿Por qué?
Analiza la situación para determinar si corresponde a una relación de variación proporcional directa, o bien, si es un ejemplo de variación proporcional inversa.
Al observar con detenimiento la tabla, es posible establecer la relación que existe entre un kilogramo de limones y el precio de 28.5 pesos, que se paga por ellos; por dos kilogramos se pagan 57 pesos, por tres kilogramos se pagan 85.5 pesos.
Lo que significa que, a mayor cantidad de kilogramos de limones comprados, es mayor la cantidad de pesos por pagar. Esto es, las cantidades relacionadas: masa y precio, o bien, sus correspondientes unidades que son kilogramos y pesos aumentan en la misma proporción; esta es una propiedad de la proporcionalidad directa.
Para comprobar que se trata de una relación de proporcionalidad directa, es importante calcular cuánto se paga por 1, 2, 3, 4 y 5, kilogramos.
Una manera de justificar la proporcionalidad directa es verificando la igualdad entre cada una de las razones, dividiendo cada uno de los valores, es decir, el precio en pesos entre su respectiva masa expresada en kilogramos; como se muestra a continuación:
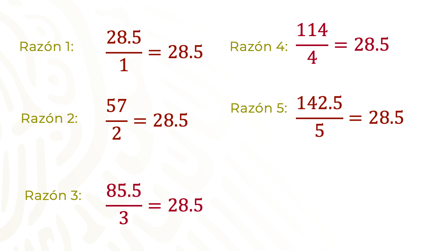
De acuerdo con los datos de la tabla anterior, se establecen las siguientes expresiones aritméticas en forma de razón, es decir, la relación del precio de los limones entre la masa en kilogramos. Por lo tanto:
Para la primera razón o relación, se tienen veintiocho punto cinco entre uno, que es igual a veintiocho punto cinco.
Para la segunda razón o relación, se tienen cincuenta y siete entre dos, que es igual a veintiocho punto cinco.
Para la tercera razón o relación, se tienen ochenta y cinco punto cinco entre tres, igual a veintiocho punto cinco.
Para la cuarta razón o relación, se tienen ciento catorce entre cuatro, que es igual a veintiocho punto cinco.
Para la quinta razón o relación, se tienen ciento cuarenta y dos punto cinco entre cinco, que es igual a veintiocho punto cinco.
En todas estas relaciones se obtuvo el mismo resultado. El 28.5 representa el valor de la unidad. Es decir, corresponde al precio de un kilogramo. A este resultado se le llama constante de proporcionalidad.

En el planteamiento:
“x” es la cantidad de kilogramos de limones.
“y” es el costo por pagar en pesos
“k” es la constante de proporcionalidad
Entonces, se establece que cuando se divide cada uno de los costos de limones “y”, entre su correspondiente masa “x” de la tabla, obtendrás a la constante de proporcionalidad “k”, con un valor de 28.5, Por lo que:
“y” entre “x” es igual a la constante de proporcionalidad “k”
Se sustituye el valor de “k” por veintiocho punto cinco y queda la expresión “y” entre “x” igual a veintiocho punto cinco.

Ahora, se despeja la literal “y”
Se retoma la expresión, veintiocho punto cinco es igual a “y” entre “x”. Se despeja “y”, es decir, dejarás sola a la literal “y”.
Como “x” está dividiendo a “y”, ahora pasará al otro lado del signo igual, multiplicando a veintiocho punto cinco.
Por lo tanto, queda la expresión:
“y” igual a veintiocho punto cinco por “x”.
La expresión representa una relación de proporcionalidad directa, entre el costo de los limones y la cantidad de kilogramos vendidos, esto es “y” es igual al producto de 28.5 por el valor de “x”.

Por ejemplo: ¿cuánto se pagará por 20 y 30 kilogramos de limones?
Para calcular el resultado, partirás de la expresión de proporcionalidad directa “y” igual a veintiocho punto cinco por “x”.
Después, se sustituye el valor de “x” en la expresión, por lo tanto, tienes que la expresión “y” es igual a veintiocho punto cinco por veinte. Multiplicando estos valores, obtendrás el producto que es quinientos setenta.
y= 28.5 (20)
y = 570
¿Qué significa este valor?
Significa que, por 20 kilogramos de limones se pagarán 570 pesos.
¿Cuánto se pagará por 30 kilogramos de limones?
Para calcular el resultado, se parte de la expresión de proporcionalidad directa “y” igual a veintiocho punto cinco por “x”. Después, se sustituye el valor de “x” en la expresión, por lo tanto, la expresión es igual a veintiocho punto cinco por treinta, multiplicando estos valores, se obtiene el producto de ochocientos cincuenta y cinco.
¿Qué significa este valor?
Significa que, por 30 kilogramos de limones se pagarán 855 pesos.
y = 28.5 (30),
y = 855
Con estos ejemplos, analizaste la resolución de situaciones-problema de proporcionalidad directa para que puedas diferenciarla de la proporcionalidad inversa.
Ahora analizarás y resolverás una situación de proporcionalidad inversa, y trabajar con su correspondiente expresión algebraica.
Ejercicio 2. La excursión.

¿La relación entre los datos es igual que la anterior o cambia? ¿Por qué?
A mayor cantidad de alumnos dispuestos a asistir a la excursión menos será el costo que deben pagar por su pasaje. A este tipo de relación se le llama proporcionalidad inversa, porque el aumento de un valor coincide con la disminución del otro, en la misma proporción.
Para demostrar que se trata de una relación de proporcionalidad inversa, debes multiplicar cada una de las cantidades de estudiantes que asistirán a la excursión con su respectivo costo, de la siguiente manera:
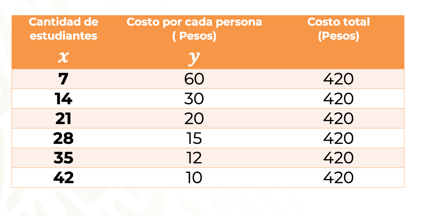
Se identifica a la variable independiente, representada con la literal “x”, en este caso corresponde a la cantidad de estudiantes, porque en relación con el número de asistentes, será el costo por pagar de cada uno. Este último representa la variable dependiente, representada por la literal “y”.
Después, se ordenan los datos como se indica en la tabla y se multiplica (la cantidad de estudiantes) por (el costo por cada estudiante).
En todas las multiplicaciones se obtiene el mismo resultado. Es decir: 420. A esta constante se le llama la constante de proporcionalidad.
¿Qué representa el resultado de las multiplicaciones realizadas en el contexto?

Ahora se despeja la literal “y”
Partiendo de la expresión cuatrocientos veinte igual a “x” por “y”

Por ejemplo, ¿cuánto pagarán si van 30 alumnos a la excursión?

Para calcular el valor de “y”, se utiliza la expresión “y” igual a cuatrocientos veinte entre “equis”, ahora debes sustituir el valor de “equis” en la expresión. Por lo tanto, ahora la expresión es igual a cuatrocientos veinte entre treinta, dividiendo, se obtiene como cociente catorce.
¿Qué significa este valor?
Significa que, por 30 estudiantes que asistan a la excursión el boleto costará 14 pesos.
A continuación, aplica lo aprendido y resuelve el siguiente problema.
Ejercicio 3. El ciclista.
Un ciclista realizó un recorrido en su bicicleta, en los primeros tres cuartos de hora (cuarenta y cinco minutos) alcanzó una rapidez de cien kilómetros por hora, pero posteriormente su rendimiento fue descendiendo.
Su entrenador registró los tiempos y la rapidez alcanzada en la tabla de recorrido.
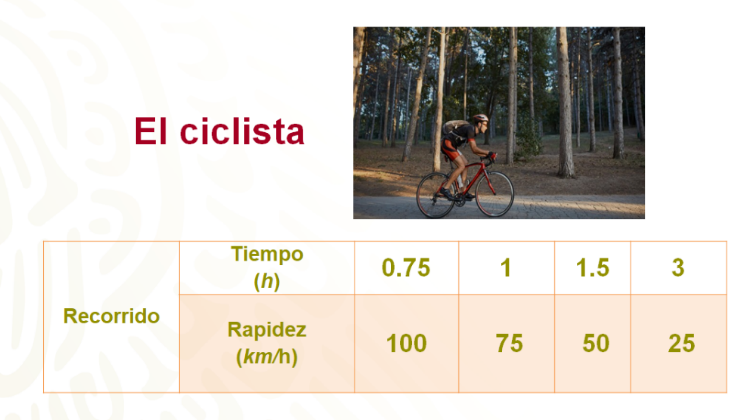
¿Qué tipo de proporcionalidad observas en la tabla de datos? ¿Por qué?
Los datos en la tabla se relacionan con la proporcionalidad inversa, porque a medida que aumenta el tiempo del ciclista durante su recorrido, la rapidez se reduce en la misma proporción.
Para verificar que se trata de una relación de proporcionalidad inversa, multiplica cada una de las cantidades, es decir, el tiempo por la rapidez, de la siguiente manera:
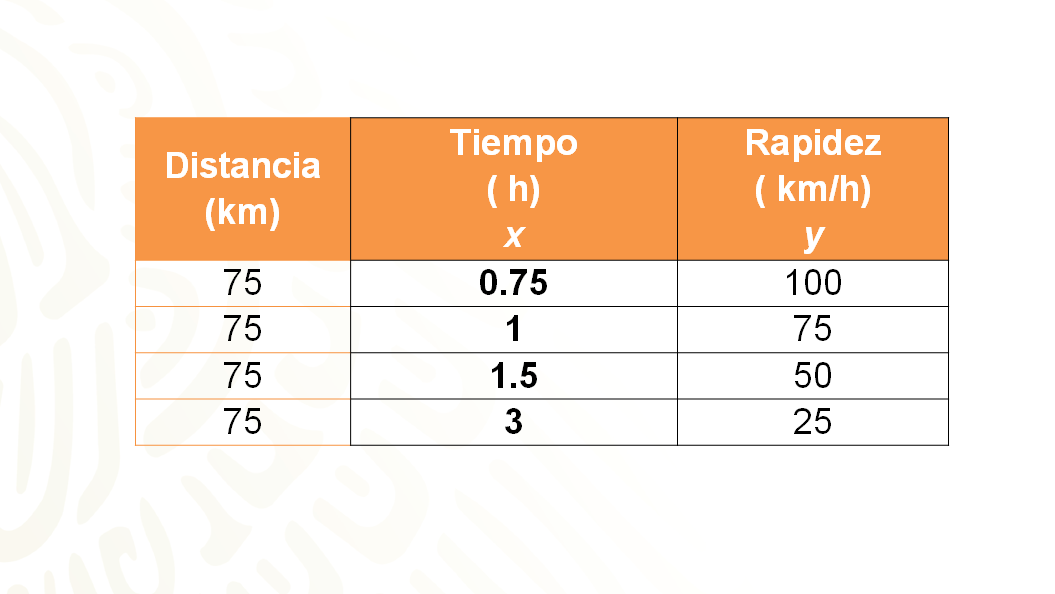
Identifica la variable independiente representada con la literal “x”, en este caso, corresponde al tiempo del recorrido, y la rapidez representa la variable dependiente representada con la literal “y”, la distancia es un dato que no está cambiando, su valor es 75 km.

Ahora, despeja la literal “y”.
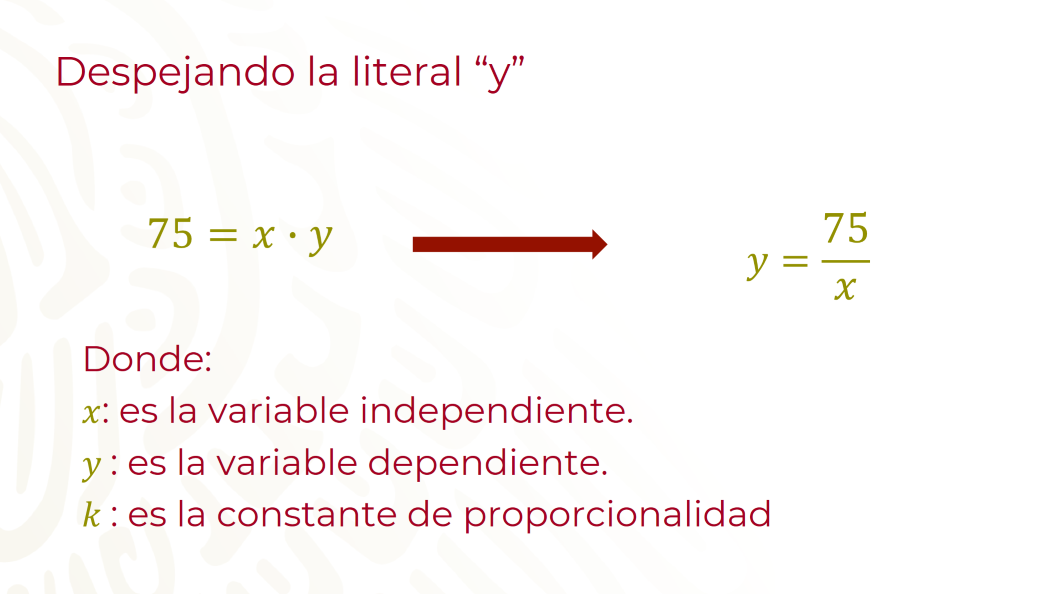
A partir de esta expresión algebraica puedes calcular la rapidez alcanzada por el ciclista.
Ahora, se quiere saber ¿qué rapidez alcanzó el ciclista en un tiempo de dos horas?
Para calcular la rapidez, partirás de la expresión “y” igual a setenta y cinco entre “x”.
Después, debes sustituir el valor de “x” en la expresión, por lo tanto, la expresión es igual a setenta y cinco entre dos, dividiendo estos valores, obtendrás como cociente treinta y siete punto cinco.

¿Qué significa este valor?
Significa que, en el recorrido de 75 km en un tiempo de 2 horas el ciclista alcanzó una rapidez de 37.5 kilómetros por hora.
Aplicando lo aprendido, realiza el siguiente ejercicio y completa la siguiente tabla de proporcionalidad:
Ejercicio 4. Los rectángulos.
Observa esta tabla, en donde se indican parte de las medidas de tres rectángulos. Uno de ellos, el rectángulo R1 tiene como base 8 cm y 3 cm de altura.

Responde lo siguiente:
¿Cuál es la base del rectángulo R2, si su altura es de 4cm?
¿Cuál es la altura del rectángulo R3, si su base es 2 cm?
¿Qué tipo de proporcionalidad observas al relacionar los datos de la tabla?
¿Qué sucede con la medida de la base de los tres rectángulos?
¿Qué sucede con la medida de la altura? ¿por qué?
A mayor medida de la altura de los rectángulos es menor la medida de la base. Si se piensa en una relación de proporcionalidad inversa, tienes que verificar que el aumento de un valor coincida con la disminución del otro, en la misma proporción.
Ordena los datos como se indica en la tabla, y multiplica (la base) por (la altura), en este caso solo puedes multiplicar una relación y es la del rectángulo uno.
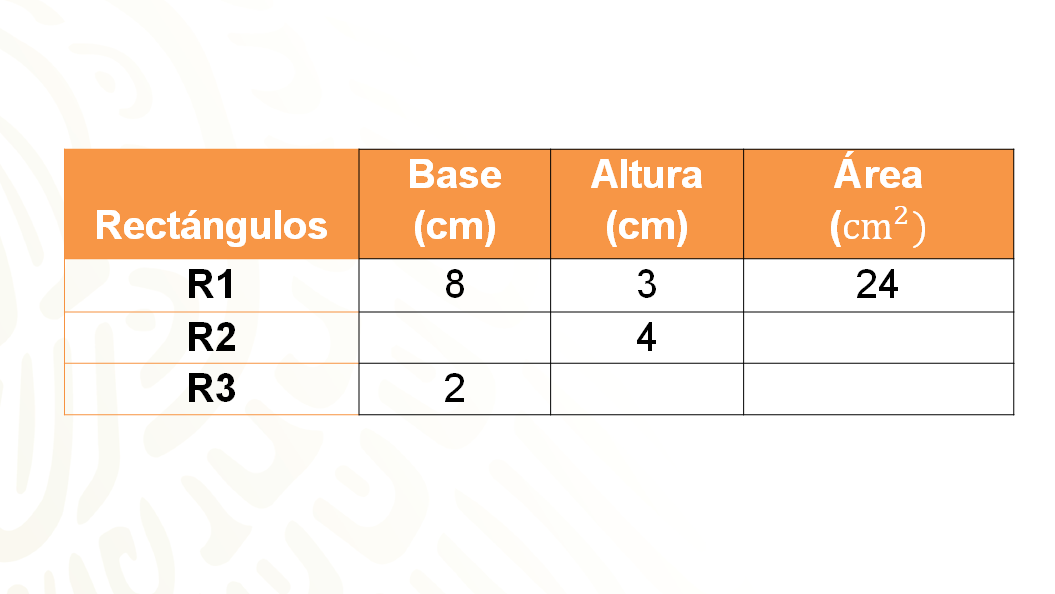
Solo se cuenta con un valor, veinticuatro, el cual tomarás como muestra constante de proporcionalidad.

Ahora despejarás el valor de “y”
Retomando la expresión veinticuatro igual a “x” por “y”.


¿Cuál es la media de la base (x) del rectángulo R2?

Para calcular la medida de la base del rectángulo R2, utilizarás la expresión “y” igual a veinticuatro entre “x”, ahora deberás sustituir el valor de “y”, que representa la altura del rectángulo en la expresión, es decir, y=4, queda cuatro igual a veinticuatro entre “x”.
Paso 1: Despejarás la “x”, es decir, dejar a la “x” sola con respecto al signo igual, como está dividiendo al veinticuatro pasara multiplicando con el cuatro y queda la expresión cuatro “x” igual a veinticuatro.
Paso 2: Para que la “x” quede sola pasaras el número cuatro a la derecha del signo igual, como está multiplicando con “x” ahora va a pasar dividiendo con el veinticuatro entonces, queda la expresión “x” igual a veinticuatro entre cuatro, al dividir las dos cantidades obtendrás como cociente 6.
¿A qué corresponde este valor? Corresponde al valor de la base del rectángulo dos (R2).

Calcula la altura del rectángulo 3 cuando la medida de la base, es decir x=2, utilizarás la expresión “y” igual a veinticuatro entre “x”, ahora deberás sustituir el valor de “x”, por lo tanto, la expresión queda “y” igual a veinticuatro entre dos, dividiéndolas dos cantidades, veinticuatro entre dos el resultado obtenido es doce.
¿A qué corresponde este valor?
Corresponde al valor de la altura del rectángulo tres (R3).
En conclusión:
¿Qué tipo de proporcionalidad observaste al relacionar a los datos de la tabla, es decir, qué sucede con la medida de la base de los tres rectángulos?
¿Qué sucede con la medida de la altura? ¿Por qué?
Puedes afirmar que se tiene una proporcionalidad inversa, ya que al disminuir la base aumenta la altura o al disminuir la altura aumenta la base, porque aritméticamente al multiplicar las relaciones de cada rectángulo el producto es veinticuatro.
A continuación, practica para seguir avanzando en tu aprendizaje.
Problema 1. Retoma el problema del ciclista:

Recuerda que esta expresión algebraica se representa de la siguiente manera:

Ahora el entrenador ha desafiado al ciclista a un nuevo reto, como parte de su entrenamiento, desea saber:
¿Qué rapidez alcanzará el ciclista en cuatro horas?
Anota todas las operaciones y responde a la pregunta anterior.
Ahora resuelve otro problema.
Problema 2. Completa la siguiente tabla con todo lo que has aprendido hasta el momento.
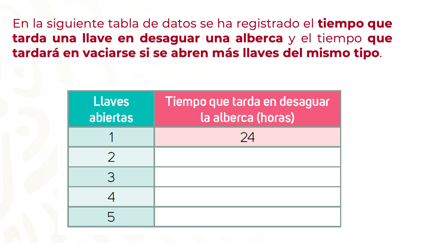
En esta clase reconociste cómo diferenciar una variación de proporcionalidad directa de otra llamada variación de proporcionalidad inversa, con base en el análisis de la correspondencia y variación entre los datos de las magnitudes que se presentan en una situación problema.
La constante proporcionalidad inversa está definida por la expresión k igual a “x” por “y”. Con esta expresión se puede encontrar el valor de las variables relacionadas en una situación de proporcionalidad inversa, y se expresan como:
“y” igual a “k” entre “x” ó “x” igual a “k” entre “y”, es decir son inversamente proporcionales.
El reto de hoy:
Pon a prueba lo aprendido hasta ahora, resolviendo algunas de las actividades de proporcionalidad directa a inversa contenidas en tu libro de texto de matemáticas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: