Proporcionalidad inversa

Proporcionalidad inversa

Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.

Énfasis: resolver problemas de proporcionalidad inversa.

¿Qué vamos a aprender?

Continuarás con el estudio de las relaciones de proporcionalidad. En esta sesión, conocerás cómo resolver problemas de proporcionalidad inversa a través de diferentes procedimientos.

¿Qué hacemos?

Para iniciar, resuelve el siguiente problema.

Problema, jardín

Se quiere construir un jardín que cumpla con ciertas condiciones: que sea de forma rectangular, que tenga un área de 24 metros cuadrados y que, el ancho del jardín pueda medir 2 metros u 8 metros; o bien, el largo del jardín pueda medir 6 metros o 5 metros.

¿Cuáles son las dimensiones que debe tener el largo y el ancho del jardín, para que se cumplan estas condiciones?

Mientras mayor es la medida del ancho del jardín, ¿la medida del largo del jardín aumenta o disminuye?

Responde las preguntas y argumenta tus respuestas.

Analiza, ¿cuál es la forma de resolver el problema? Después, describe el procedimiento que utilizarías para calcular las magnitudes que piden.

Una forma de resolver el problema es, a través del uso de una tabla de datos, la cual permite relacionar los valores conocidos para determinar los desconocidos.

El registro de datos se realiza de la siguiente manera:

En la primera columna se anotan los datos de la magnitud (a), que corresponden a la medida del ancho del jardín en metros, en la segunda columna se registran los datos de la magnitud (l), que corresponden a la medida del largo del jardín en metros; y en la tercera columna, se escribe el área que debe tener el jardín en metros cuadrados, como producto de todas las combinaciones posibles que resulten.

Toma un momento para analizar los datos de la tabla.

Observa que faltan valores que corresponden a la medida del ancho del jardín. También, faltan valores que corresponden a la medida del largo del jardín.

Sin embargo, se tiene un valor constante, el 24, que corresponde al área que debe tener el jardín. Esto se debe a que, aunque se desconozca cuanto mide el ancho o el largo del jardín, al multiplicar la medida del ancho por la medida del largo, para este caso siempre debe dar (como resultado del producto), 24.

Entonces, a partir de los datos de la tabla, ¿qué operación puedes hacer para calcular los valores que faltan?

Una división. Puedes dividir el área del jardín entre la medida del ancho, o la medida del largo del jardín; según el dato que haga falta.

Para saber, cuánto debe medir el largo del jardín cuando el ancho mide 2 metros, se debe dividir el área del jardín entre la medida del ancho del jardín, es decir, dividir 24 metros cuadrados entre 2 metros y obtienes como resultado 12 metros, que representan la medida del largo del jardín.

Ahora, para calcular la medida del ancho del jardín, cuando la medida del largo del jardín es de 6 metros, debes dividir el área del jardín entre la medida del largo del jardín; es decir, dividir 24 metros cuadrados entre 6 metros, que es igual a 4 metros, que representan la medida del ancho del jardín.

Después se repite el procedimiento para calcular, cuánto debe medir el ancho del jardín cuando la medida del largo del jardín es de 5 metros, es decir, 24 metros cuadrados entre 5 metros, que es igual a 4.8 metros, que representan la medida del ancho del jardín.

Por último, se calcula la medida del largo del jardín cuando la medida del ancho del jardín es de 8 metros; es decir, se dividen 24 metros cuadrados entre 8 metros, dando como resultado 3 metros, que representan la medida del largo del jardín.

Presta especial atención a los dibujos que representan las dimensiones del ancho y largo del jardín y compara los resultados obtenidos.

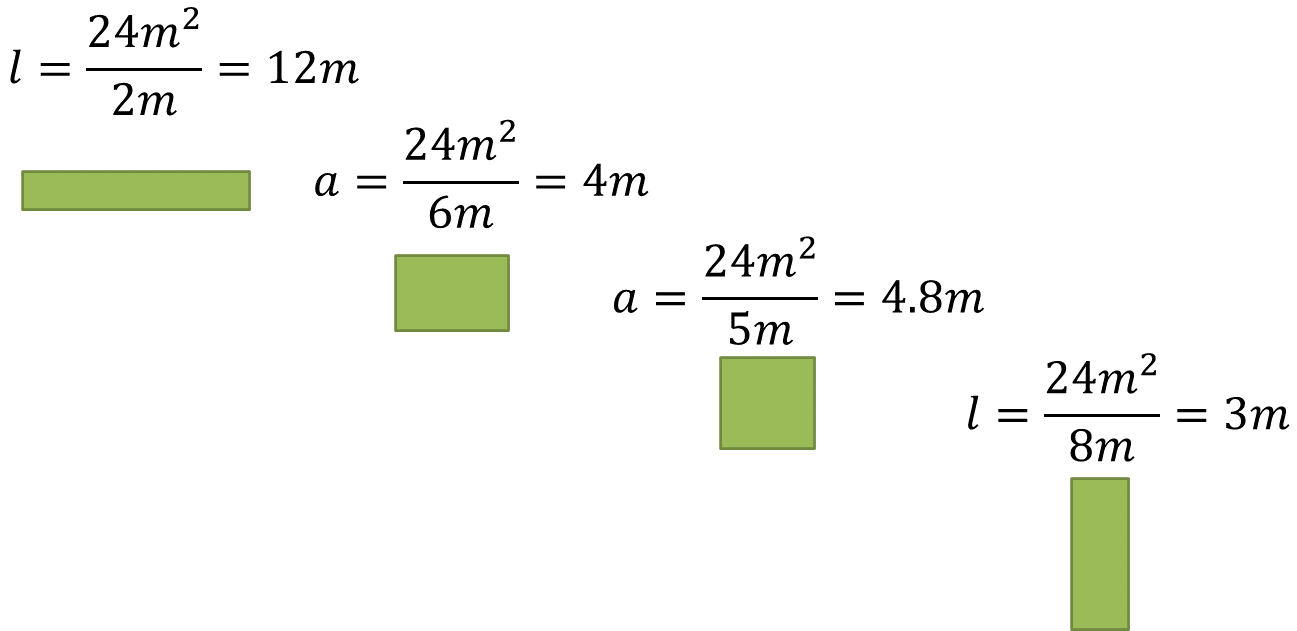
¿Notaste cómo disminuye la medida del largo mientras la medida del ancho del jardín aumenta? ¿Te diste cuenta de que el área del jardín nunca cambió?, ¿Por qué piensas que sucede eso?

Con los cálculos realizados y escritos en la tabla, ya has respondido la primera pregunta. Estos datos van a servir para responder a la segunda pregunta:

Mientras mayor es la medida del ancho del jardín, ¿la medida del largo del jardín aumenta o disminuye?

Toma un momento para reflexionar sobre la situación y después argumenta tu respuesta.

Observa cómo quedó la tabla.

Como puedes ver en la tabla, a medida que aumenta la medida del ancho del jardín, la medida del largo disminuye.

Por ejemplo, cuando el ancho del jardín aumenta de 2 metros a 4 metros, el largo del jardín disminuye de 12 metros a 6 metros, y lo mismo pasa con los demás valores.

Por lo que la respuesta a la pregunta es: la medida del largo del jardín disminuye, ya que al aumentar una de las cantidades, la otra cantidad deberá disminuir, para guardar la proporción inversa y cumplir con la condición de que el área siempre sea de 24 metros cuadrados.

Para resolver este problema, se usa la constante de proporcionalidad que se simboliza mediante la letra “k”, y la expresión algebraica para obtenerla es:

k = yx

Donde “y” representa el largo del jardín, “x” representa el ancho del jardín y “k” representa el área del jardín, que al ser un valor constante nunca va a cambiar y se obtiene del producto de “x” por “y”. Por eso, al multiplicar la medida del ancho por la medida del largo del jardín, siempre obtendrás 24 metros cuadrados.

Para calcular la medida del ancho o la medida del largo del jardín, bastará con despejar “y” o “x”, y resolver las operaciones tal como se realizó hace un instante.

En este tipo de problemas, ¿piensas que al multiplicar las cantidades correspondientes siempre obtendrás el mismo resultado? Escribe una conclusión al respecto.

Ahora, continúa con un problema más.

Problema, obreros trabajando

Observa la siguiente gráfica que muestra los días que tardan cierto número de obreros para elaborar un producto.

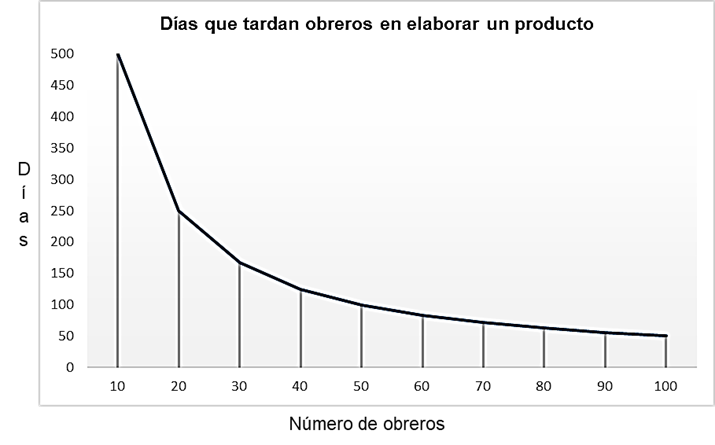
Toma unos instantes para observar la gráfica y analizarla. Después, responde las preguntas que se plantean:

¿Cuántos obreros se necesitan para elaborar el producto en 50 días? Considerando que los obreros trabajan al mismo ritmo.

Para responder a la pregunta, es necesario identificar que, en 50 días cierto número de obreros son capaces de elaborar el producto. Considerando que los obreros trabajan al mismo ritmo.

Por lo tanto, se debe ubicar ese dato en la gráfica y leer el valor que le corresponde en el número de obreros.

La respuesta es 100 obreros. Es decir, se necesitan 100 obreros para elaborar el producto en 50 días, todos trabajando al mismo ritmo.

Con 20 obreros trabajando, ¿en cuántos días se elaboraría el producto?

Ahora debes centrar tu atención en el eje “x”, que corresponde al número de obreros y ubicar los 20 obreros ahí, para después identificar el valor que le corresponde en el eje “y”, que indica los días de trabajo.

La respuesta es 250 días. Es decir, si sólo 20 obreros trabajan, el producto se elaboraría en 250 días.

Ahora, si se duplica el número de obreros de la pregunta anterior:

¿El número de días para elaborar el producto también se duplica?

Toma un momento para pensar, y argumenta tu respuesta.

En la pregunta anterior se contaba con 20 obreros, ahora se pide que se duplique esa cantidad, por lo tanto, habrá 40 obreros trabajando.

Al disponer de más obreros trabajando, se espera que, el número de días de trabajo disminuya, eso significa que la respuesta a la pregunta es: no se duplica, porque a mayor número de obreros trabajando, menor es el número de días que tardarán en elaborar un producto, y eso se puede ver en la gráfica.

Identifica en la gráfica, la línea que une los 20 obreros y los días de trabajo. Después sigue el recorrido de la gráfica que va de 20 a 40 obreros y te darás cuenta de que, al duplicarse el número de obreros, los días de trabajo disminuyen de manera inversamente proporcional. Lo que significa que, si los obreros se duplican; por ejemplo, por dos; los días de trabajo se disminuyen por la mitad, es decir, entre dos.

Por lo tanto, al aumentar una cantidad al doble, la cantidad correspondiente a ella hace lo opuesto. Es decir, si una cantidad se duplica, la otra se divide por la mitad. Y si se triplica o cuadriplica, ¿Qué pasa con la cantidad correspondiente? Escribe una conclusión al respecto.

A continuación, resuelve el siguiente problema.

Problema, pintura de un muro

3 personas tardan 12 horas en pintar un muro, ¿cuántas personas trabajando de manera constante serían necesarias si se quiere pintar el mismo muro en 4 horas?

Cuando no cuentas con el apoyo de una tabla de valores o de una gráfica para resolver problemas de proporcionalidad inversa, existen algunos algoritmos matemáticos que te ayudarán a resolver estos problemas, uno de ellos es mediante la representación de las proporciones.

El valor que se pretende conocer es el del número de personas y puedes representarlo con una “x”, que simboliza el número de personas que se requieren para pintar el muro en 4 horas.

Lo que debes hacer ahora es, acomodar los datos en forma de tabla, posteriormente, generar los productos de las dos cantidades que representen la constante de proporcionalidad. Para finalmente, realizar los cálculos necesarios y resolver el problema.

Se representan las magnitudes en dos columnas. La primera se titulará como “personas” y se escriben los datos que corresponden al número de personas, en este caso 3 y x.

La segunda columna se titulará como “horas” y ahí se escribe 12 y 4, que son las horas que tardarían en pintar el muro 3, y “x” número de personas respectivamente.

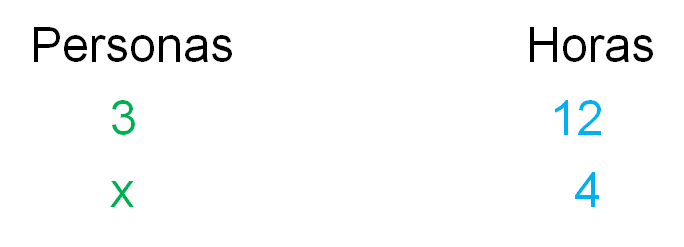
La relación de que 3 personas tardan 12 horas genera el producto 3 por 12. La relación de que “x” personas tardan 4 horas, genera el producto x por 4. Después, se igualan los productos y se tiene que 3 por 12 es igual a 4x. Se resuelven los productos y se obtiene treinta y seis es igual a 4x.

Aplica las propiedades de la igualdad, para despejar “x” y encontrar su valor, y se obtiene que treinta y seis cuartos es igual a x. Resuelve el cociente para calcular el valor de “x” y se obtiene que “x” es igual a 9.

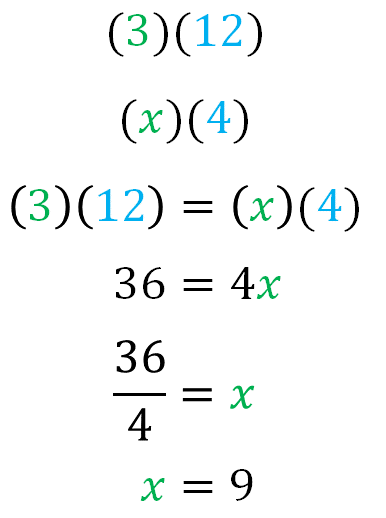
Con este valor calculado se puede responder la pregunta y dar solución al problema. Entonces se puede decir que, 9 personas serían necesarias para pintar el muro en 4 horas, todas ellas trabajando al mismo ritmo.

Pero ¿qué pasa si se quiere que el muro sea pintado en menos tiempo?, por decir, en 2 horas.

¿Se necesitarían un mayor número de personas o un menor número de personas?

Al disminuir el tiempo aumenta el número de personas que pintan el muro. Ahora, sólo tienes que realizar los cálculos, para comprobar el resultado.

Como se sabe que se necesitan 9 personas para pintar el muro en 4 horas, ya tienes la primera relación: que es 9 por 4. La segunda estará dada por la relación, “x” personas tardan 2 horas, es decir, “x” por 2. Se resuelven las operaciones y se obtiene, treinta y seis es igual a 2x. Ahora, aplica las propiedades de la igualdad para despejar “x” y se obtiene que, treinta y seis medios es igual x.

Resuelve el cociente y se obtiene que, “x” es igual a 18.

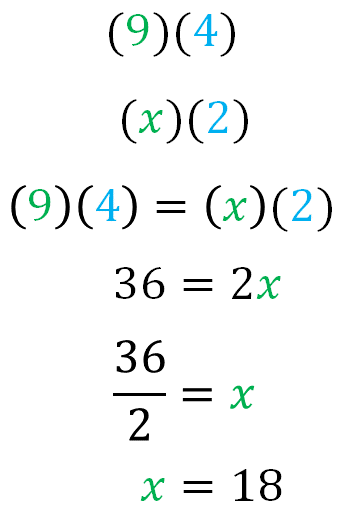
Entonces, se puede decir que, para pintar el muro en 2 horas se necesitarían 18 personas. Es decir, la cantidad de personas aumenta para poder pintar el muro en menos tiempo.

Resuelve un último problema.

Problema, magnitudes

La siguiente tabla muestra cómo se relacionan dos magnitudes diferentes, de manera inversamente proporcional. En la primera fila se tienen los valores de la magnitud “A”. En la segunda fila están los valores de la magnitud “B”.

Analiza los datos que aparecen en la tabla y cómo es que están relacionados tanto en forma horizontal como en forma vertical.

Reflexiona sobre si la manera en que están relacionados los datos de la magnitud “A”, es la misma forma en que están relacionados los datos de la magnitud “B”. También reflexiona sobre la relación que existe entre cada pareja de datos de diferentes magnitudes.

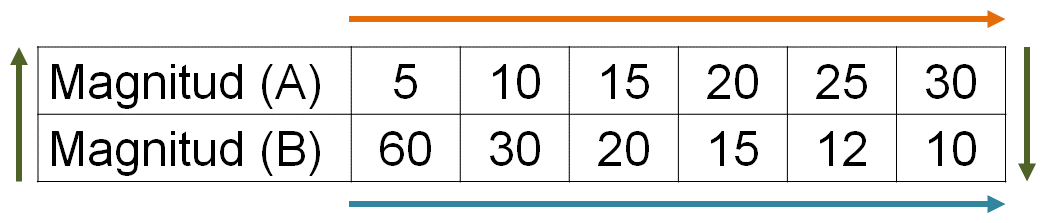
Ahora, vas a explorar las relaciones que existen entre los datos de la tabla.

A partir de los datos de la tabla:

¿Puedes justificar porque están relacionados de manera inversamente proporcional?

Toma un momento para pensar tus respuestas.

Observa nuevamente la tabla, analiza cada pareja de datos de diferentes magnitudes y reflexiona:

¿Qué sucede con ellos?

Por ejemplo:

¿El primer dato de la magnitud A es el doble o la mitad del primer dato de la magnitud B, o viceversa?

Si se divide cada pareja de datos de las diferentes magnitudes, ¿se obtiene como resultado siempre el mismo valor?

Si se multiplica cada pareja de datos de las diferentes magnitudes, ¿se obtiene como resultado siempre el mismo valor?

Si por lo menos una de tus respuestas es sí, ¿eso qué significa?

Observa qué sucede y responde las preguntas anteriores.

A simple vista puedes darte cuenta de que, el primer dato de la magnitud “A”, no es el doble ni la mitad de la magnitud “B” y viceversa. Es decir, el 5 no es el doble de 60, ni 60 es el doble de 5. Tampoco el 5 es la mitad de 60, ni 60 es la mitad de 5.

Ahora, si se realizan los cocientes de cada pareja de datos, por ejemplo 5 entre 60 y 10 entre 30, te puedes dar cuenta que el resultado es diferente; y lo mismo pasa con las demás parejas de datos.

Lo mismo pasa si se cambia el dividendo por el divisor, ya que 60 entre 5 es diferente de 30 entre 10. Sucede lo mismo con las demás parejas de datos.

Ahora, multiplica cada pareja de datos de diferente magnitud:

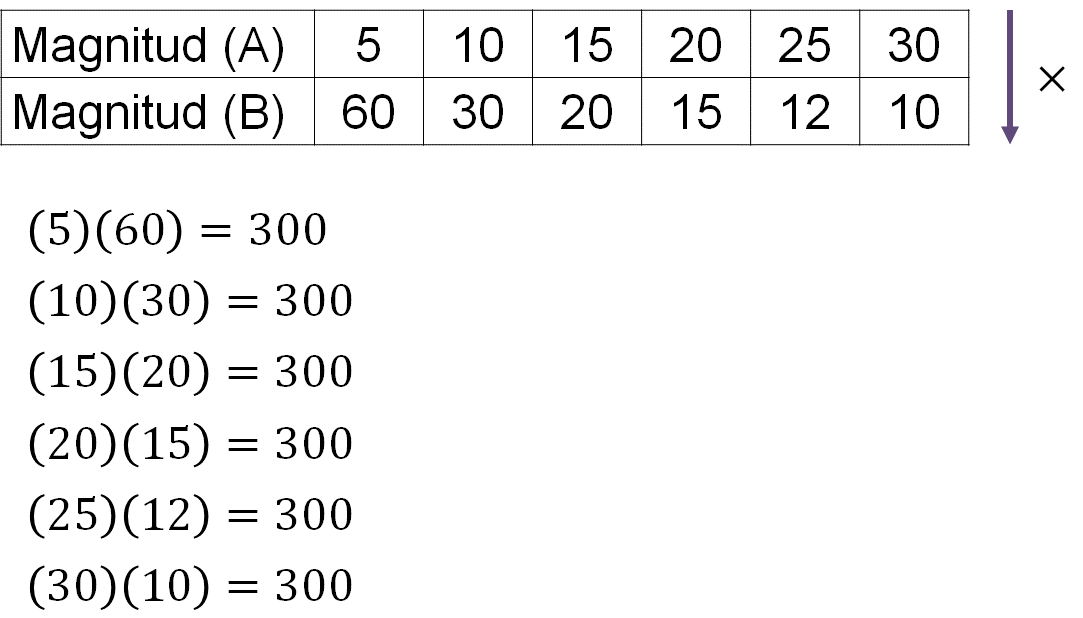
¿Estos resultados qué significan?

En el problema del jardín el área siempre era 24 metros cuadrados. En los datos de esta tabla sucede lo mismo con el resultado, siempre será el mismo.

Esto significa que se cuenta con un valor que se repite y se llama constante de proporcionalidad inversa, por lo tanto, se puede decir que los datos de la tabla son inversamente proporcionales, porque el producto de sus variables es constante.

Otra manera de saber si los datos de dos magnitudes están relacionados de manera inversamente proporcional, es analizando los datos horizontalmente a través de las razones de cada magnitud. Observa la tabla.

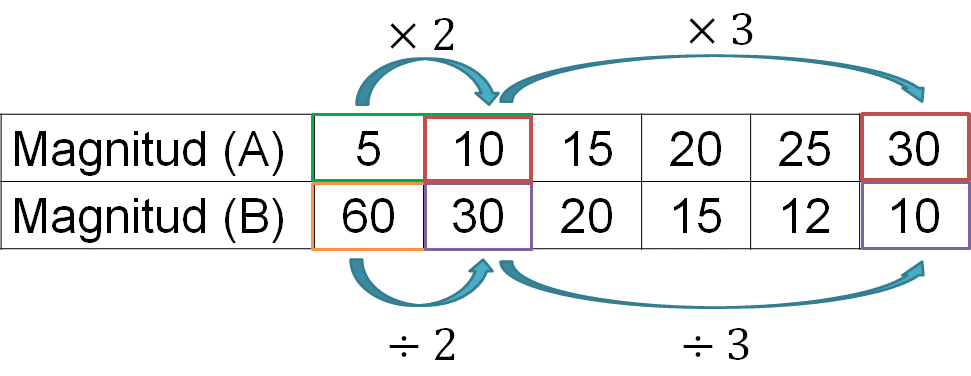
Observa la primera pareja de números de la magnitud “A” y la primera pareja de números de la magnitud “B”, analiza los datos preguntándote, ¿cuántas veces aumentó la magnitud A? y ¿qué pasa con los datos de la magnitud B?

Como pudiste darte cuenta, la primera cantidad de la magnitud A se duplicó, mientras que la primera cantidad de la magnitud B disminuyó por la mitad.

Continúa con otra pareja de datos, la razón 10 a 30 de la magnitud “A” y la razón 30 a 10 de la magnitud “B”.

La primera cantidad de la razón de la magnitud “A” se triplicó. Entonces, esto quiere decir que ya sabes que la segunda cantidad de la razón de la magnitud “B” es, un tercio de la primera cantidad de la misma magnitud.

Lo anterior quiere decir que, en una relación de proporcionalidad inversa, si un valor de una magnitud se multiplica por cualquier número, el valor de la cantidad correspondiente (de la otra magnitud), queda dividido por el mismo número. Por ejemplo, si se triplica un valor, su correspondiente se divide por tres.

Ahora, piensa que los valores de la magnitud “A” corresponden a la magnitud tiempo, y también que, los valores de la magnitud “B” corresponden a la magnitud de la velocidad, es decir, a la rapidez.

¿Podrías hacer algunas afirmaciones sobre los valores de la tabla y las magnitudes?

Toma un momento para pensarlo.

Una afirmación puede ser que el tiempo y la magnitud de la velocidad son magnitudes inversamente proporcionales porque a mayor tiempo, menor es la magnitud de la velocidad para una misma distancia recorrida.

Otra afirmación podría ser que la distancia recorrida es una constante de proporcionalidad inversa, porque el producto del tiempo por la magnitud de la velocidad siempre da el mismo resultado, es decir, la distancia siempre es la misma.

Otra afirmación puede ser que, al quíntuple del tiempo le corresponde una quinta parte de la magnitud de la velocidad.

Escribe tus afirmaciones en tu cuaderno y coméntenlas a distancia con tus compañeras y compañeros.

Hasta este momento has logrado resolver diferentes problemas de proporcionalidad inversa.

El primero usando la constante de proporcionalidad (k), el segundo a través del análisis de una gráfica de proporcionalidad inversa, el tercero a través de su representación algebraica por medio de sus proporciones, y el último a través del análisis de los valores de las magnitudes.

También analizaste el comportamiento de las relaciones de las magnitudes y cantidades involucradas, por lo que se puede concluir que:

Los productos de las cantidades que son correspondientes son constantes, a esa característica se le conoce como, constante de proporcionalidad inversa. Por ejemplo, en el problema del jardín, siempre que se multiplicaba la medida del ancho del jardín por la medida del largo del jardín, se obtenían 24 metros cuadrados.

También se puede concluir que dos cantidades son inversamente proporcionales sí, y sólo si, al aumentar una de las cantidades la otra cantidad disminuye en la misma proporción. Por ejemplo, en el problema de la gráfica pudiste ver que cuando se duplica el número de obreros de 20 a 40, los días de trabajo disminuían por la mitad.

Otra conclusión es que dos cantidades son inversamente proporcionales sí, y sólo si al disminuir una de las cantidades la otra cantidad aumenta en la misma proporción. Por ejemplo, en el problema del muro y las personas para pintarlo, se disminuyó el tiempo de 4 horas a 2 horas para pintar el muro, por lo que el número de personas aumentó de 9 a 18.

Con todo el trabajo que has realizado y las conclusiones que se han elaborado, ya cuentas con las herramientas necesarias para resolver problemas de proporcionalidad inversa.

Hemos llegado al final de la sesión, dedicada a la resolución de problemas de proporcionalidad inversa.

Recuerda que este es un material de apoyo y para complementar lo estudiado, puedes consultar otras fuentes como tu libro de texto de Matemáticas de segundo grado.

El reto de hoy:

Resuelve el siguiente problema de proporcionalidad inversa.

Problema, planta purificadora

Toda el agua que produce una planta purificadora se puede envasar en 840 envases de medio litro de capacidad.

¿Cuántos envases de 1.5 litros, un cuarto de litro y 3 litros de capacidad se necesitarían para envasar la misma cantidad de agua?

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/