Proporcionalidad directa e inversa
Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.
Énfasis: analizar situaciones problemáticas que se resuelven mediante relaciones de variación de proporcionalidad y argumentar el resultado obtenido.
¿Qué vamos a aprender?
Identificarás diferentes situaciones a través de problemáticas que se resuelven mediante relaciones de proporcionalidad para definir a qué tipo de variación corresponden: directa, inversa o múltiple. Asimismo, aplicarás varios de los conocimientos que has adquirido en las últimas sesiones.
¿Qué hacemos?
Analizar el siguiente problema.
Luis elabora cajas artesanales que tienen forma hexagonal para venderlas en su negocio familiar: tienen una tienda de regalos. Para la realización de cada caja debe cortar 2 plantillas como las siguientes:

De un pliego de cartoncillo logra obtener 10 cajas pequeñas. ¿Cuántos pliegos de cartoncillo necesita para elaborar 35 de esas cajas?
Antes de dar respuesta a la pregunta planteada, verifica si existe una relación de proporcionalidad entre las cantidades o magnitudes implicadas en el problema.
En caso de que haya una relación de proporcionalidad, ¿es directa o inversa? Recuerda que dos magnitudes son proporcionales cuando cumplen con una relación de correspondencia entre dos razones que son equivalentes.
Primero, analiza las razones.
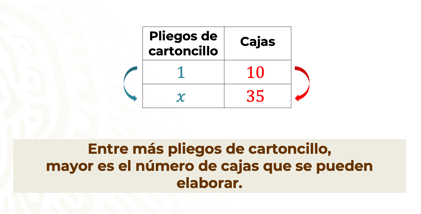
En los datos de la tabla se identifica que con un pliego de cartoncillo se elaboran 10 cajas. Y si se compara el número de cajas que se obtienen de un pliego de cartoncillo con la cantidad de cajas que se necesita obtener, se observa que, entre más pliegos de cartoncillo, mayor es el número de cajas que se pueden elaborar:
Con 1 pliego se elaboran 10 cajas
Con 2 pliegos se elaboran 20 cajas.
Con 3 pliegos se elaboran 30 cajas.
Con 4 pliegos se elaboran 40 cajas.
Los datos de la columna “pliegos de cartoncillo” están relacionados proporcionalmente con los datos de la columna “Cajas”, pues sus razones o factores internos son iguales; la razón entre 1 y 10 es la misma que entre 2 y 20.
Por lo tanto, se identifica que sí existe una relación de proporcionalidad. Y además se trata de una relación de proporcionalidad directa.
Porque al aumentar los pliegos de cartoncillo, también aumenta la cantidad de cajas, pues las dos magnitudes aumentan en la misma proporción.
Entonces, ¿Cuántos pliegos de cartoncillo se necesitan para elaborar 35 cajas?
Resuelve el problema: Comienza por establecer la proporción a partir de los datos que conoces:
(1 es a 10 como “x” es a 35).

Multiplica 1 por 35 y luego divide el producto entre 10, de tal manera que tienes: 3.5 como cociente.
Esto significa que para hacer 35 cajas se necesitan 3 y un medio pliegos de cartoncillo.
No olvides que, en una relación de proporcionalidad directa, siempre se cumple que el cociente de la división de cualquiera de las magnitudes en “y” entre su correspondiente magnitud en “x”, es constante. Al valor obtenido de esta operación se le conoce como constante de proporcionalidad.
Lo anterior se verifica. Cuando al dividir el número de cajas entre la correspondiente cantidad de pliegos de cartoncillo se obtiene como constante 10. Tal como se puede observar en la imagen.
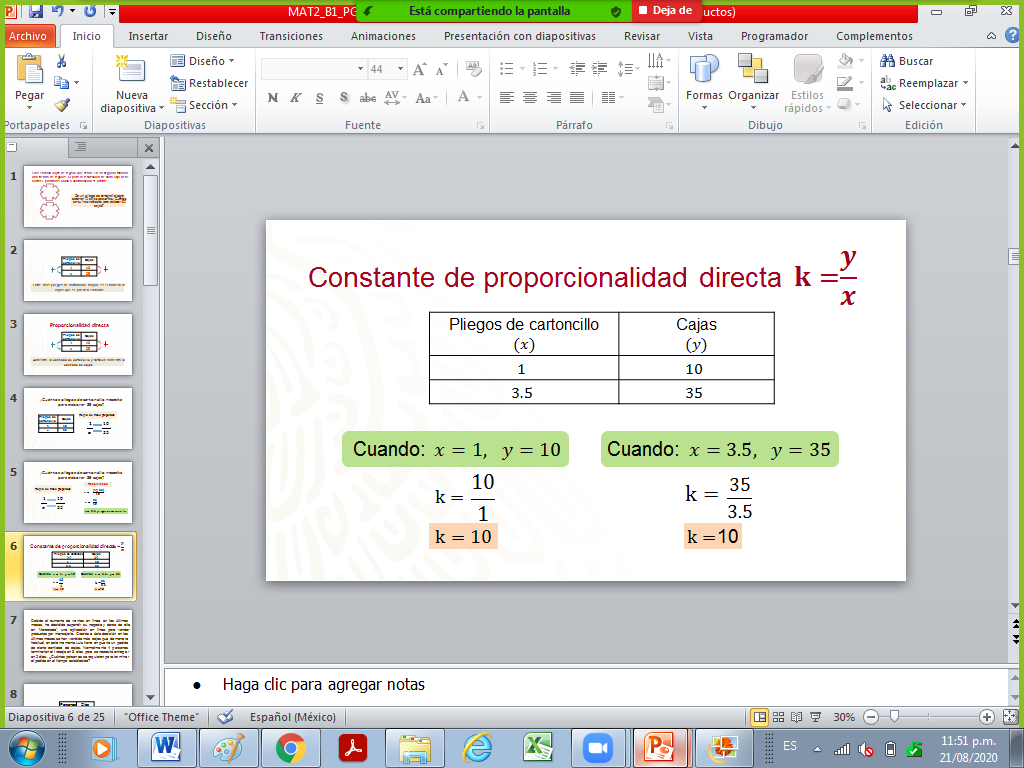
La resolución de este problema te ayudó a saber que Luis necesitará tres y medio pliegos de cartoncillo para 35 cajas.
Ahora observa otro desafío que enfrenta Luis.

Primero, revisa las condiciones establecidas para ver si existe o no una relación de proporcionalidad.
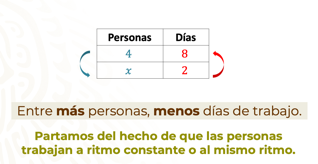
Si analizas detenidamente la situación, te darás cuenta de que cuando aumentan el número de personas, disminuyen los días invertidos en la elaboración de cajas y al considerar que las personas trabajan a ritmo constante o al mismo ritmo, se puede decir que se trata de una relación de proporcionalidad inversa.
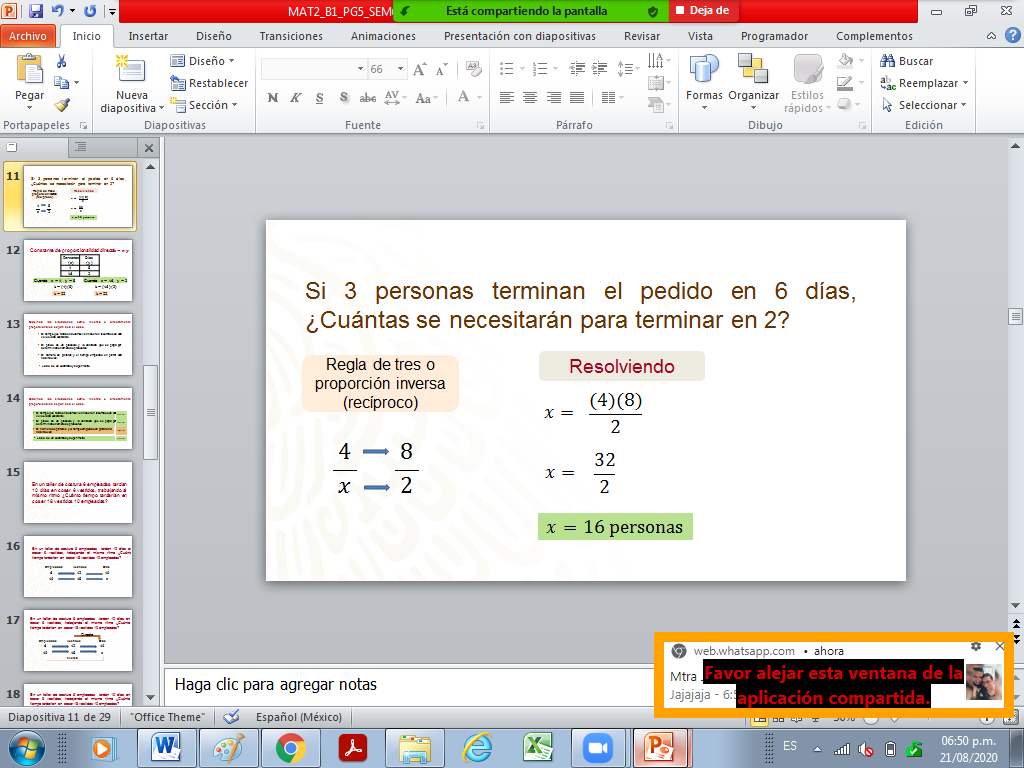
Recuerda que, para resolver una proporción inversa el proceso de resolución es distinto, en este caso, se trabaja con el recíproco de una fracción. Como a continuación se observa.
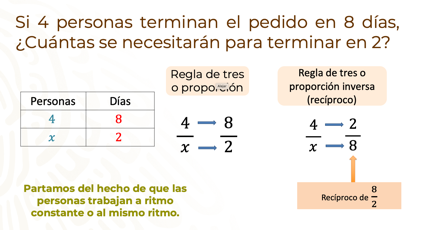
Se necesita el recíproco de que es para establecer la proporción y resolverla. Multiplica 4 por 8, y divide el resultado entre 2, de esta manera sabrás que se necesitan 16 personas para terminar el pedido en el tiempo establecido, es decir, en dos días.
Entonces, si dos magnitudes son inversamente proporcionales, se cumple que el producto de la multiplicación de cualquiera de las magnitudes en “x” por su correspondiente magnitud en “y”, siempre será constante. Al valor obtenido se le conoce como constante de proporcionalidad inversa.
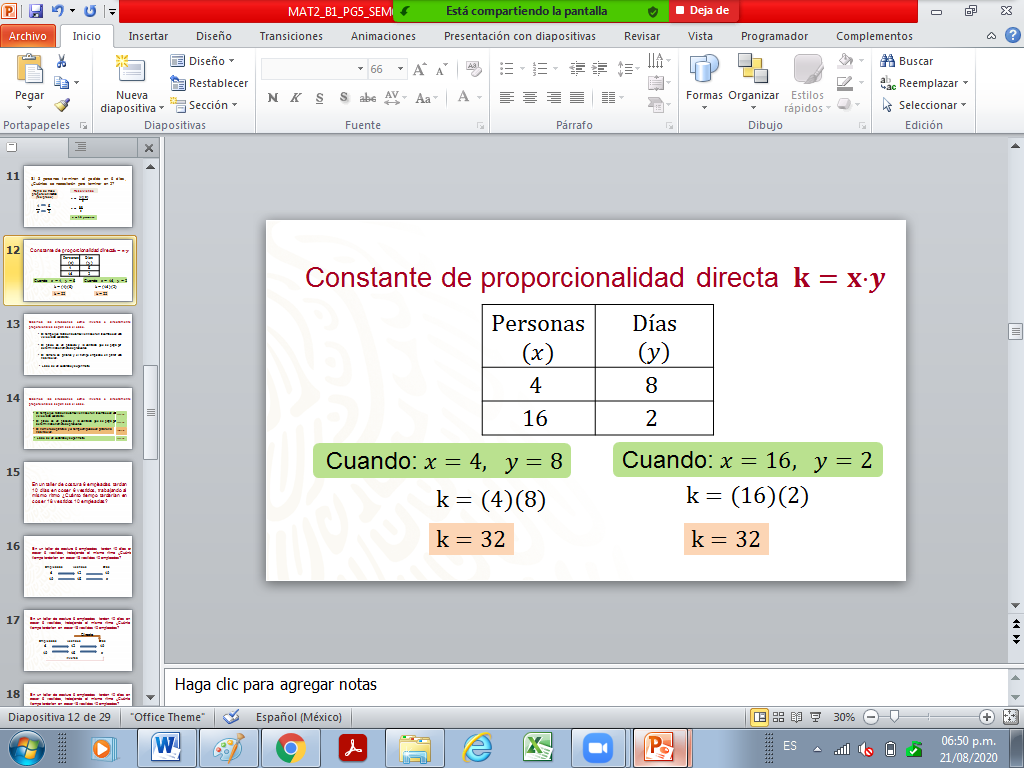
En este caso la constante de proporcionalidad inversa es 32.
A continuación, realiza la siguiente actividad.
Observa y analiza las siguientes situaciones. Y responde ¿en qué caso se trata de una relación de proporcionalidad directa y en qué caso de una relación de proporcionalidad inversa?

Después de haber terminado la actividad, verifica tus resultados con la siguiente imagen y analiza.
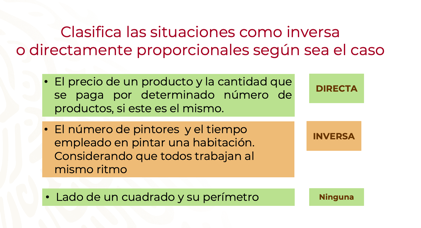
Primera situación:
- El precio de un producto y la cantidad que se paga por determinado número de productos, si este es el mismo, representa una relación de proporcionalidad directa, ya que el precio por producto es constante, de manera tal que, entre más productos, mayor es el precio por pagar.
Segunda situación: - El número de pintores y el tiempo empleado en pintar una habitación, considerando que todos trabajan al mismo ritmo. Representa una relación de proporcionalidad inversa, debido a que, al aumentar el número de pintores, disminuye el tiempo de trabajo, en la misma proporción.
Tercera situación - Por último, la medida del lado de un cuadrado y su perímetro, no representa una relación de proporcionalidad directa ni inversa, pues para que tenga sentido hablar de proporcionalidad es necesario que haya al menos 4 cantidades en juego: dos que se relacionan con otras tantas. No tiene sentido decir que el lado de un cuadrado y su perímetro están en relación proporcional.
A continuación, revisarás diferentes situaciones de proporcionalidad. Analiza el siguiente planteamiento.

Ahora reflexiona en lo siguiente:
¿Identificas alguna diferencia en éste nuevo planteamiento?
Se trata de una relación de proporcionalidad, pero a diferencia del problema anterior, ahora intervienen 3 magnitudes. A este tipo de relación en donde existe proporcionalidad, no solo entre dos sino entre más de dos magnitudes, se le conoce como proporcionalidad múltiple, de manera que, a partir de las relaciones establecidas, se obtiene la desconocida.
Es importante saber que, en una relación de proporcionalidad múltiple pueden estar presentes relaciones de proporcionalidad directa y relaciones de proporcionalidad inversa, o ambas.
Resolver un problema de este tipo, requiere de análisis, pero no es tan complicado si se utiliza lo que has aprendido hasta ahora.
Para comenzar, tienes que analizar las condiciones que se establecen. Con el fin de facilitar el proceso, primero ordena los datos como se muestra en la imagen:

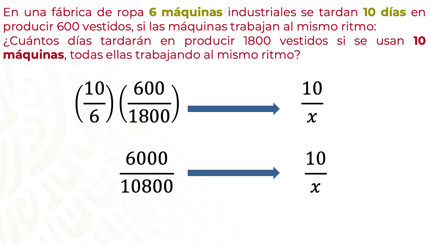
Se escriben los datos del problema de manera que queden de la siguiente manera: número de máquinas con máquinas, vestidos con vestidos y días con días, de tal forma que: 6 máquinas producen 600 vestidos en 10 días; como 10 máquinas, producen 1800 vestidos en un número desconocido de días.
Ya que cuentes con esta información, procede a identificar si se trata de una relación de proporcionalidad directa, inversa, o ambas.

Entre las razones establecidas, hay una en la que se desconoce un valor, esta razón es la que tomarás como referencia para compararla con las otras dos.
De esta manera, sólo se compara la cantidad de máquinas con el tiempo de producción de vestidos.
Si analizas cuidadosamente la situación te puedes dar cuenta de que, a mayor número de máquinas, menor será el tiempo invertido en la producción de los vestidos. Por lo tanto, la cantidad de máquinas y la cantidad de días representan una relación de proporcionalidad inversa.
En primer lugar, compara las dos razones de las que se conocen todas las magnitudes con la razón en donde aparece el dato faltante.
Después de haber acomodado los datos, considera que la relación entre la cantidad de máquinas de coser y la cantidad de días es inversamente proporcional, y se escribe el recíproco de qué es , esto con la finalidad de resolver la proporción.

Multiplica las magnitudes; en este caso 10 por 600 y 6 por 1800.
De esta manera obtendrás
Entonces se tiene que 6000 es a 10, como 10800 es a “x”.
La segunda relación establecida entre las magnitudes es de proporcionalidad directa. Por este motivo, se resuelve con la regla de tres como una proporción directa.
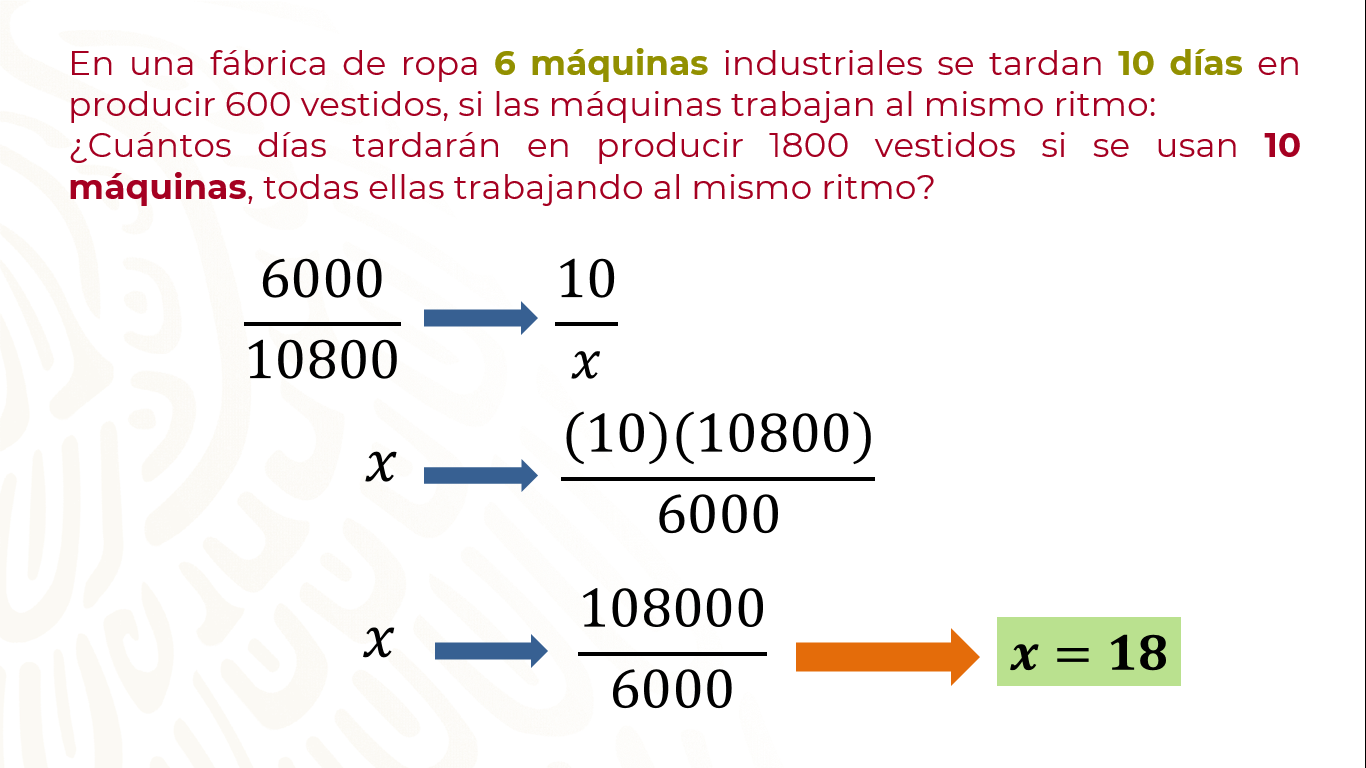
Entonces, se multiplica 10 por 10800 y al resultado se divide entre 6000. Obteniendo el valor de 18.
Así sabrás que en 18 días las 10 máquinas terminarían de producir los 1800 vestidos.
Ahora, observa un ejemplo más. Pon a prueba lo que hasta ahora has aprendido con el siguiente problema.

Considera que el problema plantea que los trabajadores mantienen un ritmo de trabajo constante. Nuevamente se trata de una relación de proporcionalidad múltiple, ya que en ella se relacionan 3 magnitudes, siendo necesario establecer una comparación entre las cantidades que intervienen en el problema.
Con este propósito, se organiza la información en: días, trabajadores y metros; como se muestra en la siguiente imagen para establecer las razones, y se representa al valor desconocido con la letra “x”.

Identifica la razón en la que está el dato faltante y la comparas con cada una de las razones restantes para definir el tipo de relación que existe entre ellas.
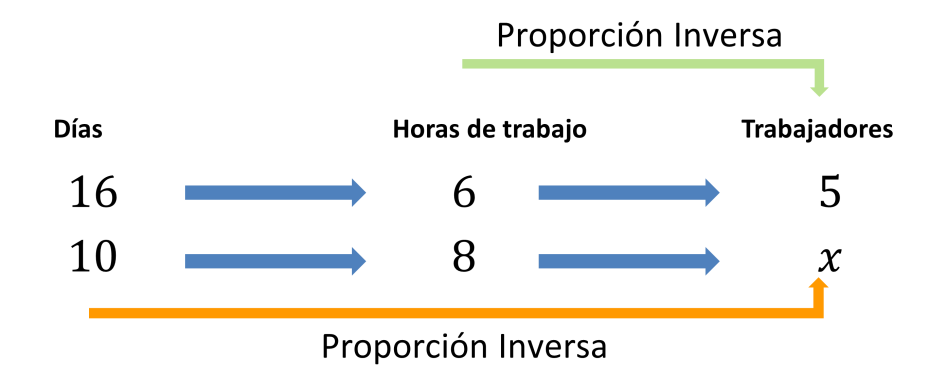
Si comparas la cantidad de días con el número de trabajadores, te darás cuenta de que, entre menos días, se requiere mayor cantidad de trabajadores, por lo tanto, se establece una relación de proporcionalidad inversa.
Y si comparas las horas de trabajo con el número de trabajadores, enseguida notaras que, si aumentan las horas de trabajo, disminuye la cantidad de trabajadores. Por lo tanto, también representa una relación de proporcionalidad inversa.
Ahora resuelve. Al tratarse de una relación de proporcionalidad inversa-inversa, se opera con los recíprocos de las magnitudes días y horas de trabajo, es decir y , de las que sus recíprocos son: y respectivamente.
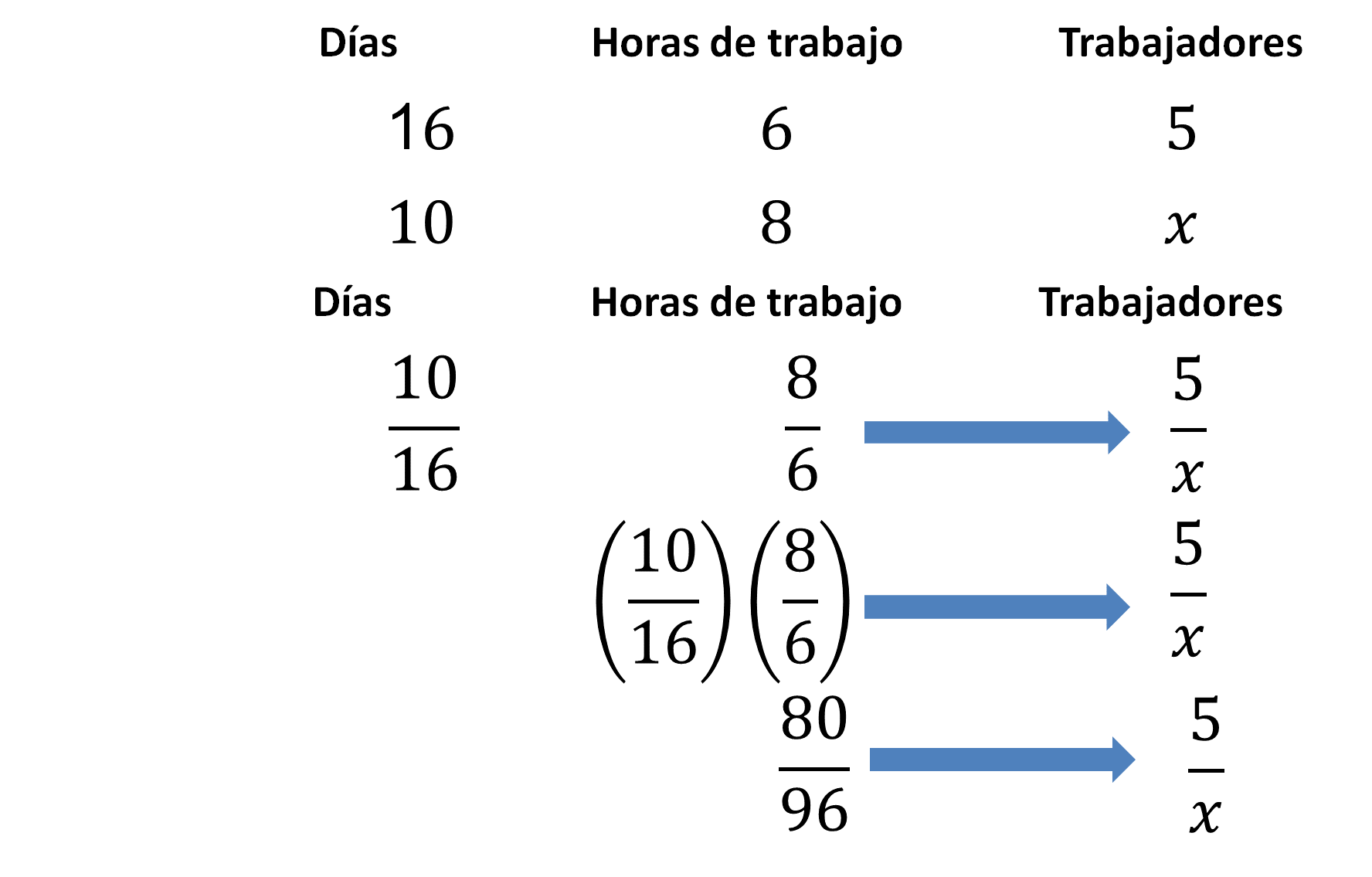
De esta manera se multiplica por y se obtiene como resultado
Ahora solo resuelve la proporción que se ha establecido. Para hacer más fácil el proceso, puedes simplificar la fracción hasta su mínima expresión que es:
Y resolverás la proporción multiplicando 6 por 5 y dividiendo el resultado entre 5.
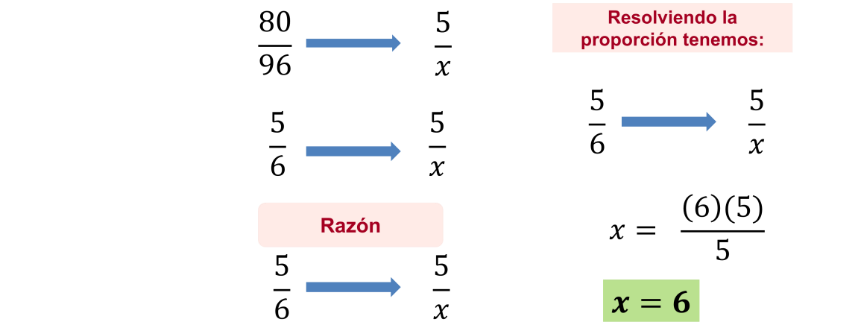
De esta manera sabrás que se necesitan 6 trabajadores para poder construir la bodega. Trabajando 8 horas diarias durante 10 días, manteniendo un ritmo de trabajo constante.
Una dificultad frecuente es resolver aditivamente los problemas en lugar de aplicar la constante multiplicativa. Para ello, en cada problema identifica las magnitudes o razones involucradas, y verifica su igualdad al compararlas.
Otra dificultad es tratar de memorizar las reglas o procedimientos sin comprenderlos previamente. La memoria ocupa un papel importante en tu aprendizaje, pero sobre todo necesitas comprender el sentido de las reglas y las relaciones que hay entre los procedimientos. Por ello, debes de aclarar todas tus dudas antes de continuar avanzando en los temas. La aplicación mecánica de los pasos puede ayudar, siempre y cuando hayas comprendido el significado de ellos.
Por último, recuerda que una vez que hayas obtenido la respuesta de un problema, hay que buscar que esta tenga sentido y significado en el contexto; lo que implica comprender los saberes matemáticos necesarios para que tu encuentro con las matemáticas sea grato, satisfactorio y placentero.
Para dar seguimiento a esta lección, anotar tus reflexiones sobre lo visto. Además, revisa y profundiza lo aprendido en tu libro de texto de Matemáticas de segundo grado.
El reto de hoy:
Reto de lógica. “La lente biconvexa”.
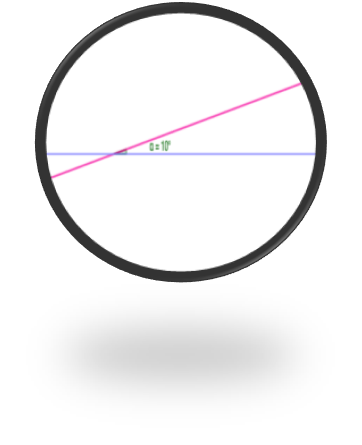
Con una lupa, que aumenta cinco veces, se están observando dos rectas que forma un ángulo de diez grados.
Responde a la pregunta: ¿Con qué magnitud se ve el ángulo?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
