Propiedades de traslación de una figura
Propiedades de traslación de una figura
Aprendizaje esperado: explica el tipo de transformación (reflexión, rotación o traslación) que se aplica a una figura para obtener la figura transformada. Identifica las propiedades que se conservan.
Énfasis: analizar las propiedades de traslación de figuras.
¿Qué vamos a aprender?
Estudiarás las propiedades de traslación y rotación de una figura; identificarás las propiedades que se conservan en la simetría; construirás diseños que combinaran la simetría axial y central, la rotación y traslación de figuras, hasta lograr que puedas trasformar una figura por medio de la homotecia.
Comenzarás por saber que es la traslación, cómo puedes llevarla a cabo, para que más adelante puedas construirla. Necesitarás tu cuaderno, lápiz y las escuadras de tu juego de geometría.
¿Qué hacemos?
Antes de empezar lee el siguiente texto, es del libro “El hombre que calculaba”. En el capítulo 2, Beremís cuenta la historia de su vida y de los prodigiosos cálculos que realizaba.
“Me llamo Beremís Samir y nací en la pequeña aldea de Khoy, en Persia, a la sombra de la gran pirámide formada por el monte Ararat. Siendo muy joven todavía, me empleé como pastor al servicio de un rico señor de Khamat. Todos los días, al salir el Sol, llevaba el gran rebaño al campo, debiendo ponerlo al abrigo, al atardecer. Por temor de extraviar alguna oveja y ser por tal negligencia castigado, las contaba varias veces durante el día. Fui, así, adquiriendo, poco a poco, tal habilidad para contar que, a veces, instantáneamente, calculaba sin error el rebaño entero. No contento con eso, pasé a ejercitarme contando además los pájaros cuando, en bandadas, volaban por el cielo. Me volví habilísimo en ese arte. […], mi bondadoso patrón acaba de concederme algunos meses de descanso, y por eso voy ahora a Bagdad pues deseo visitar a algunos parientes y admirar las bellas mezquitas y los suntuosos palacios de esa bella ciudad. Y para no perder el tiempo, me ejército durante el viaje, […].
Y señalando una vieja y grande higuera que se erguía a poca distancia, prosiguió:
– Aquel árbol, por ejemplo, tiene doscientas ochenta y cuatro ramas. Sabiendo que cada rama tiene, término medio, trescientas cuarenta y siete hojas, se deduce fácilmente que aquel árbol tendrá un total de noventa y ocho mil quinientas cuarenta y ocho hojas. ¿Qué le parece, amigo?
– ¡Qué maravilla! –exclamé atónito-. ¡Es increíble que un hombre pueda contar todos los gajos de un árbol, y las flores de un jardín! Tal habilidad puede proporcionar a cualquier persona un medio seguro de ganar envidiables riquezas.
– ¿Cómo es eso? –preguntó Beremís-, ¡Jamás pasó por mi imaginación que pudiera ganarse dinero contando los millones de hojas de los árboles o los enjambres de abejas! ¿Quién podría interesarse por el total de ramas de un árbol o por el número de pájaros que cruzan el cielo durante el día?
– Vuestra admirable habilidad – expliqué- podría ser empleada en veinte mil casos diferentes. En una gran capital como Constantinopla, o aún en Bagdad, seríais un útil auxiliar para el Gobierno. Podríais calcular poblaciones, ejércitos y rebaños. Fácil os sería evaluar las riquezas del país, el valor de las colectas, los impuestos, las mercaderías y todos los recursos del Estado.”
¿Quieres saber qué sigue y de las soluciones que Beremís da a las situaciones a las que se enfrenta? Continúa la lectura de “El Hombre que Calculaba” de Malba Tahan de los Libros del Rincón.
¿Conoces la palabra traslación? Podrías imaginar, ¿dónde la utilizas en tu vida cotidiana?
Escribe en tu cuaderno dos ejemplos, donde consideres que estás usando la traslación y más adelante podrás verificar si lo que hiciste está correcto.
Recuerda que debes escribir lo primero que se te ocurra. En las siguientes imágenes, observa cuáles son las que mantienen la forma y el tamaño. Anota en tu cuaderno las que hayas elegido.

Revisa tus respuestas.
Si respondiste que las imágenes eran: el camión, la motoneta, el globo aerostático, el avión y el carro, estás en lo correcto, ya que esas figuras además de ser las mismas, se encuentran en la misma dirección.
Recuerda que la traslación es el movimiento de un cuerpo de un lugar hacia otro lugar.
Teniendo en cuenta este concepto, ¿qué ejemplos son los que anotaste en tu cuaderno y que consideraste cómo traslación?
- Un elevador cuando sube o cuando baja.
- Una puerta corrediza cuando se abre o se cierra.
- La ventana de un automóvil cuando la abres o la cierras.
- Cuando juegas ajedrez y mueves algunas de sus piezas.
Ahora bien, la traslación de figuras en el campo de la geometría (una rama de las matemáticas), consiste en el movimiento de una figura geométrica, pero sin cambiar su forma ni su tamaño, es decir, la figura geométrica no gira ni cambia de tamaño, solo se traslada dentro de un plano.
Realiza la siguiente actividad:
En tu cuaderno, traza el plano cartesiano como se muestra en la siguiente imagen:
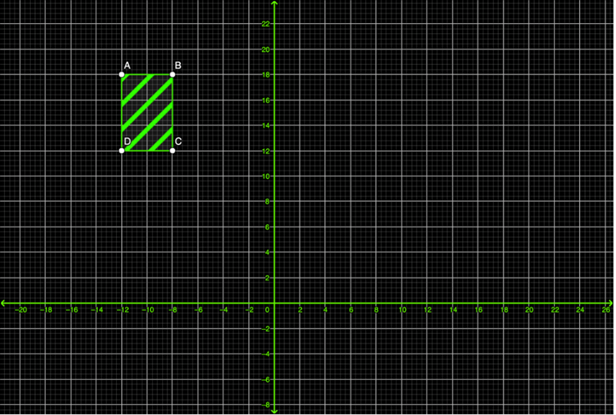
Traza el rectángulo que está de color verde. Cuando termines realiza lo siguiente:
Mueve el rectángulo 7 cuadros hacia la derecha y 4 hacia abajo.
Recuerda que la figura no gira, ni cambia de tamaño. ¿Cómo te quedó la figura?
¿Lograste trasladarla?
Observa si lo hiciste de la siguiente manera:
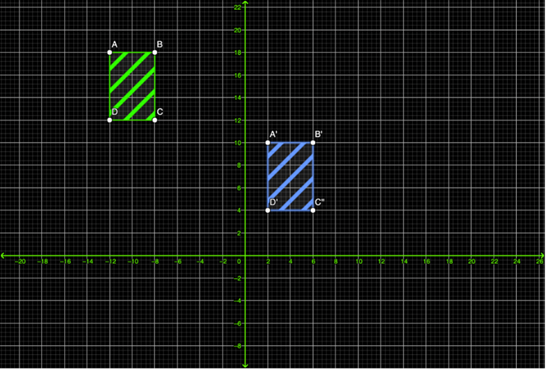
Lo que hiciste fue mover la figura y cambiarla de lugar conservando la misma forma y tamaño, es decir, sigue siendo la misma figura, pero a una cierta distancia.
Observa que el cuadrilátero ABCD, al trasladarlo obtuviste el cuadrilátero A prima, B prima, C prima y D prima en donde sus vértices, lados y ángulos son homólogos, es decir, los elementos de cada cuadrilátero corresponden a los elementos del otro cuadrilátero.
Ahora bien, observa cuales son las características de las figuras cuando han sido trasladadas.
Las propiedades de traslación son las siguientes:

La directriz nos indica hacia dónde moverás la figura, todos los vértices se mueven en la misma dirección.
La longitud es la distancia del movimiento de la figura. La longitud que une dos puntos homólogos, también se le conoce como amplitud del movimiento.
Observa estas propiedades en la siguiente figura:
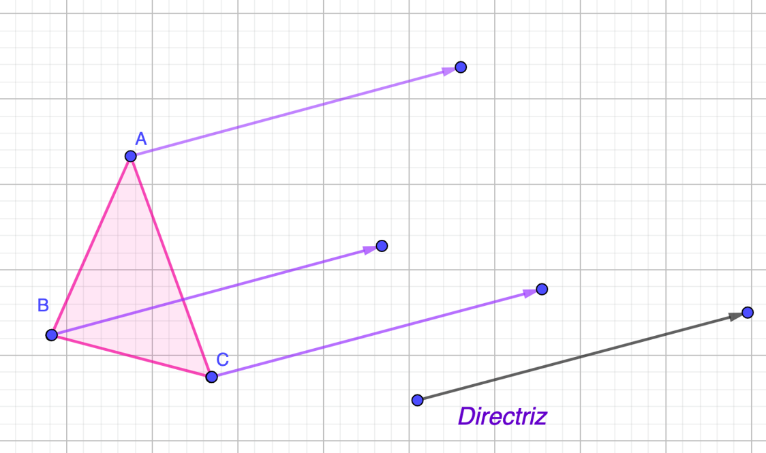
En este caso, el triángulo indica cual será la directriz del movimiento, es decir, la dirección hacia dónde moverás la figura.
Cómo puedes observar el siguiente triángulo, lo trasladarás 7 unidades, lo cual es indicado por la longitud. Todos los vértices deben tener la misma longitud, para que la figura sea la misma.
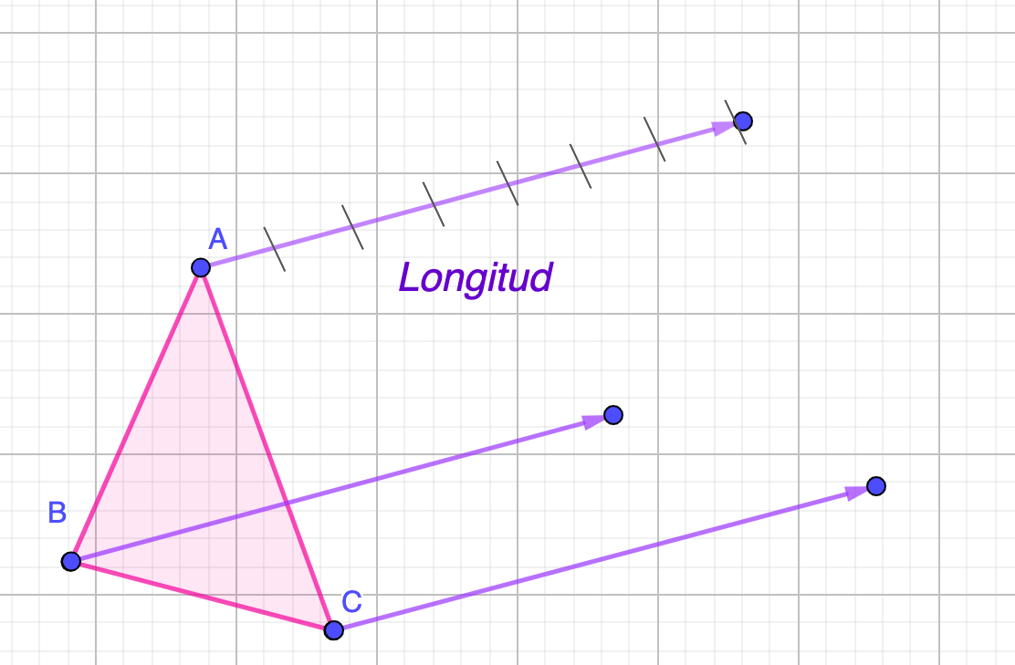
Lo que falta, es unir los vértices homólogos para formar la figura trasladada. Todos los puntos del triángulo describen trayectorias que son segmentos iguales y paralelos entre sí.
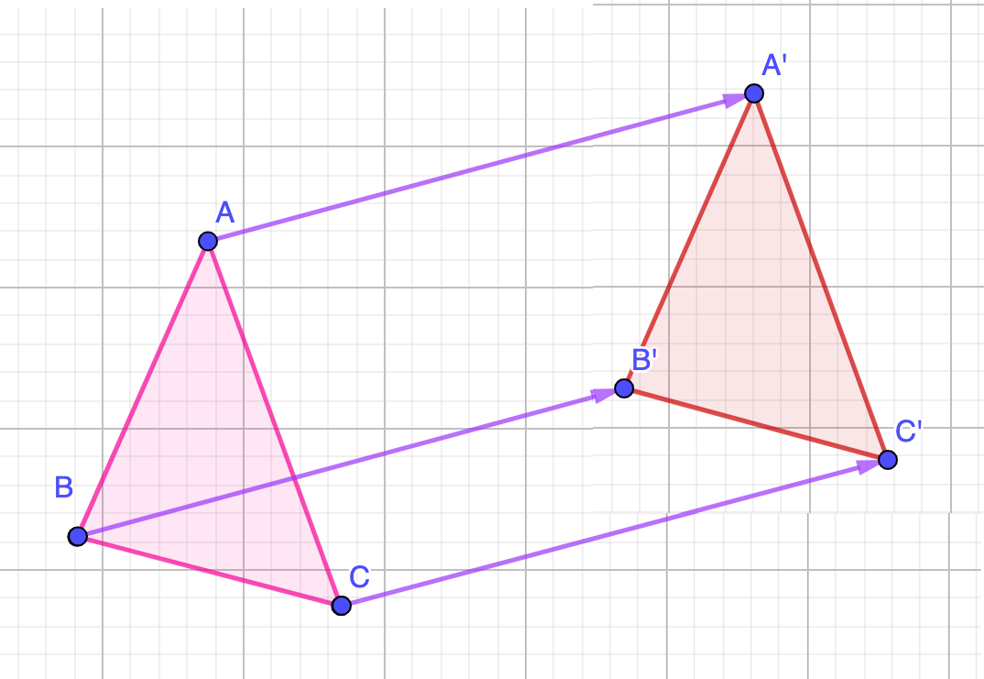
Como podrás darte cuenta, se conserva la medida de sus lados, la medida de sus ángulos, su tamaño y su forma.
Cualquier segmento de la figura es paralelo al mismo segmento de su imagen.
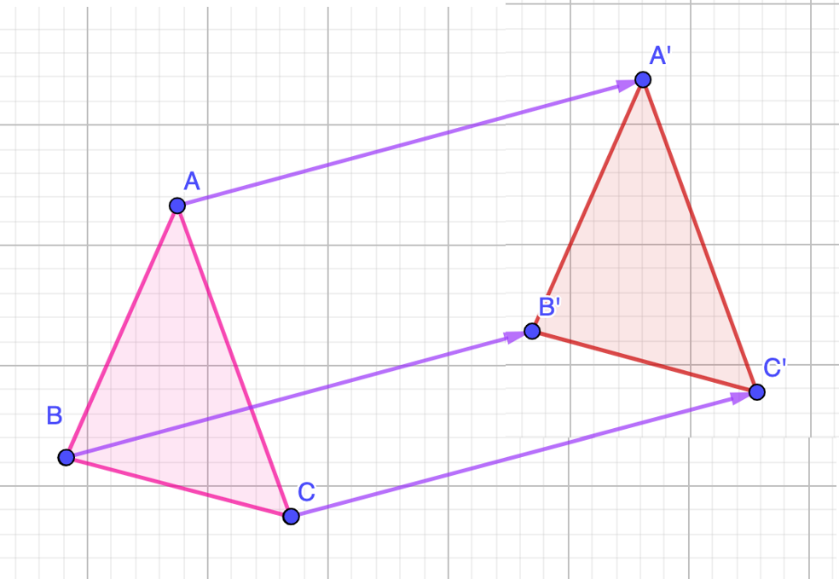
A continuación, conocerás algunas situaciones que resolverás para conocer más de este tema.
Situación 1.
José Manuel va llegando de su escuela y encuentra a su papá muy entretenido, se acerca a él y le pregunta, ¿Qué es lo que haces?
A lo que el papá le responde, estoy buscando la manera de acomodar unas figuras de un juego que yo jugaba hace algunos años.
José Manuel le pregunta ¿Podrías explicarme en qué consiste el juego?
El papá le dice que el juego consiste en ir acomodando las figuras que van saliendo, de tal manera que no queden espacios entre ellas. Ya que el objetivo del juego es ir formando líneas de manera horizontal.
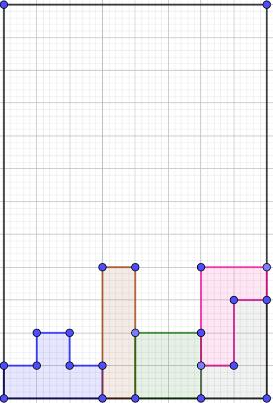
En ese momento el papá de José Manuel le pregunta ¿cómo le harías para acomodar la figura que va saliendo?, si deseo acomodarla en la parte punteada.
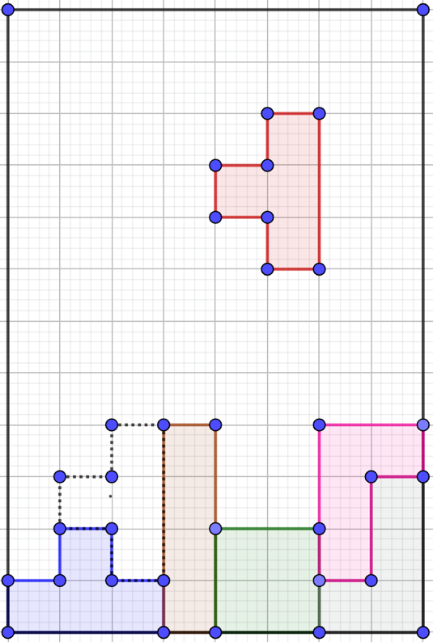
¿Cuál crees que sea la respuesta que dé José Manuel a su papá?
Y tú, ¿qué respuesta le darías?
¿Hacia dónde se tendría que mover la figura, hacia la derecha o hacia la izquierda?
¿Cuántos espacios tendría que bajar la figura José Manuel para que quede en el lugar que le dijo su papá?
Observa la respuesta que dio José Manuel a su papá.
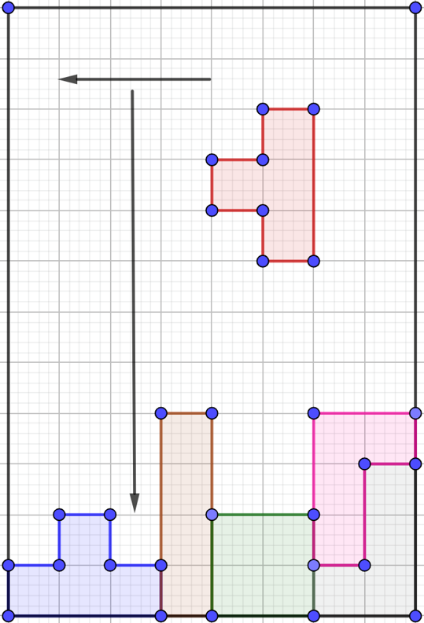
Primero la figura tiene que avanzar 3 espacios hacia la izquierda y 6 espacios hacia abajo.
¿Coincidiste en tus respuestas?
Situación 2.
Observa ahora un ejercicio de un libro de texto de tercer grado de secundaria, recuerda que puedes buscar el tema en tu libro y realizar los ejercicios que tengan que ver con el tema.

Responde:
¿Cuál es la diferencia entre el cuadrilátero 1 y el 2? ¿Y entre el 1 y el 3?
¿Qué puedes observar aquí?
¿Lograste identificar las diferencias?
Los tres cuadriláteros son los mismos, sin embargo, entre el cuadrilátero 1 y 2, la diferencia es que están en diferente posición. En cambio, entre el cuadrilátero 1 y 3, se encuentran en la misma posición.
Resuelve el siguiente ejercicio:
En tu cuaderno traza un plano cartesiano donde contemples los 4 cuadrantes, y que los valores de ambos ejes vayan desde 7 negativo hasta 7 positivo, una vez que lo tengas dibuja el polígono como se muestra a continuación:
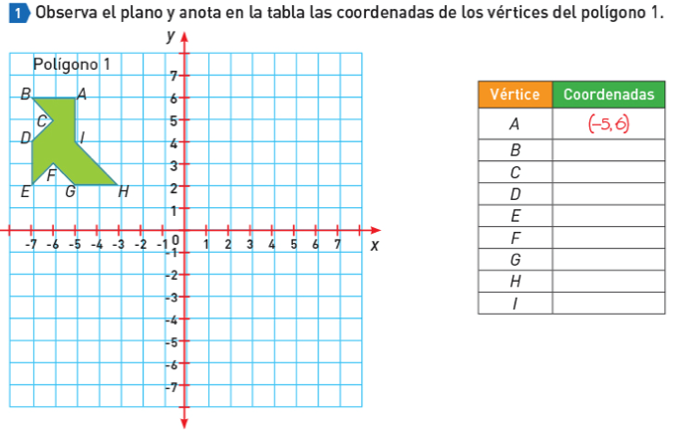
La indicación que es: observa en el plano y anota en la tabla las coordenadas de los vértices del polígono 1.
Si te fijas bien en el polígono 1, está trazado en el segundo cuadrante del plano cartesiano, por lo que los valores de las abscisas, es decir, los valores en el eje x, serán negativos y los de las ordenadas, los valores en el eje y, serán positivos.
Por lo que, para el vértice A, las coordenadas son 5 negativo y 6 positivo.
Recuerda que, para ubicar las coordenadas, primero ubicas el valor de las abscisas y luego ubicas el valor que está en las ordenadas.
Entonces, ¿cuáles son las coordenadas para los demás vértices?
Resuelve:
Observa el polígono 1 y ubica el vértice B.
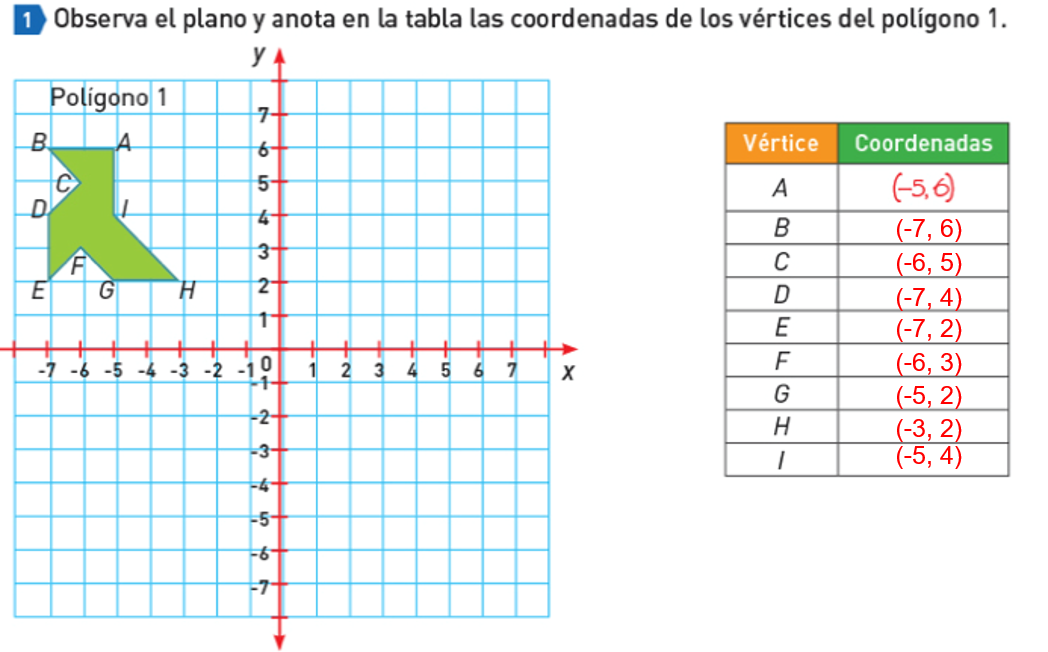
Ahora bien, traslada el polígono 8 lugares a la derecha de su actual posición. ¿Qué implica este movimiento? ¿Cuáles son las nuevas coordenadas del polígono?
Observa bien, como antes el valor de la abscisa era 5 negativo y se piden que se traslade 8 lugares a la derecha, el resultado será 3 positivo. El valor de la ordenada se deja tal cual.
Y así encontraste la nueva coordenada para A prima.

Recuerda que las abscisas corresponden a los valores de x. Por lo que, para el vértice A prima, las coordenadas ahora serían 3 positivo y 6 positivo.
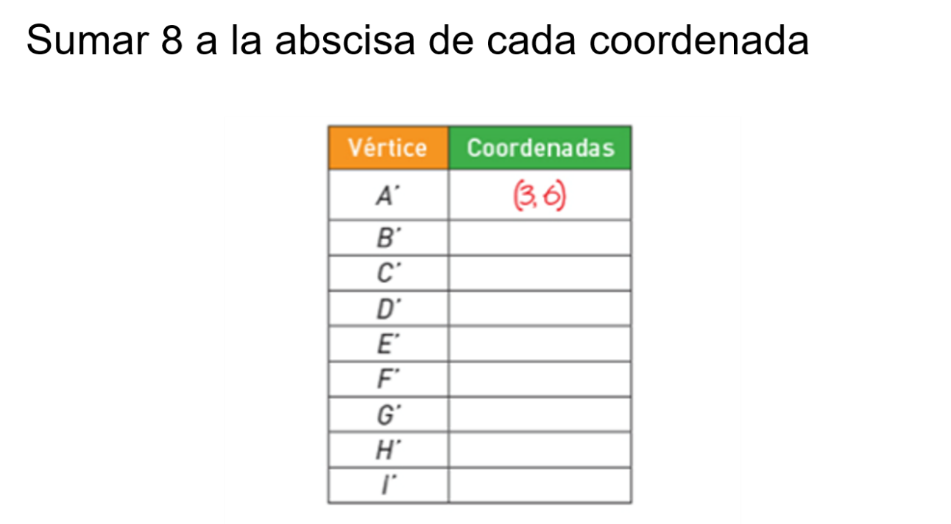
Ahora haz lo mismo con todas las coordenadas.
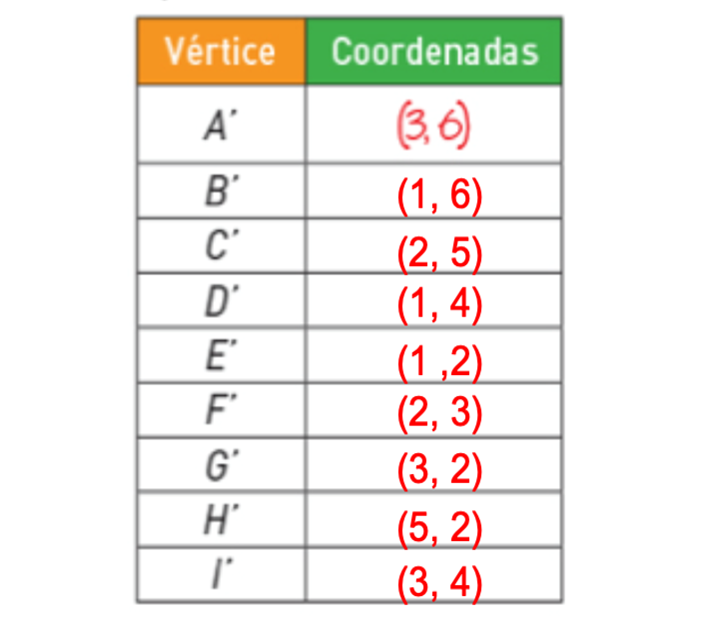
¿Lograste obtener estos valores en todas sus coordenadas?
Ahora bien, localiza las coordenadas A prima, B prima, C prima…hasta I prima, en el plano cartesiano y únelos ordenadamente con segmentos para formar el polígono 2.
¿Cómo fue el polígono que acabas de formar?
Compáralo con lo que realizaste. ¿Lograste formar la misma figura?
Si comparas el polígono 1 con el polígono 2, ¿son iguales?
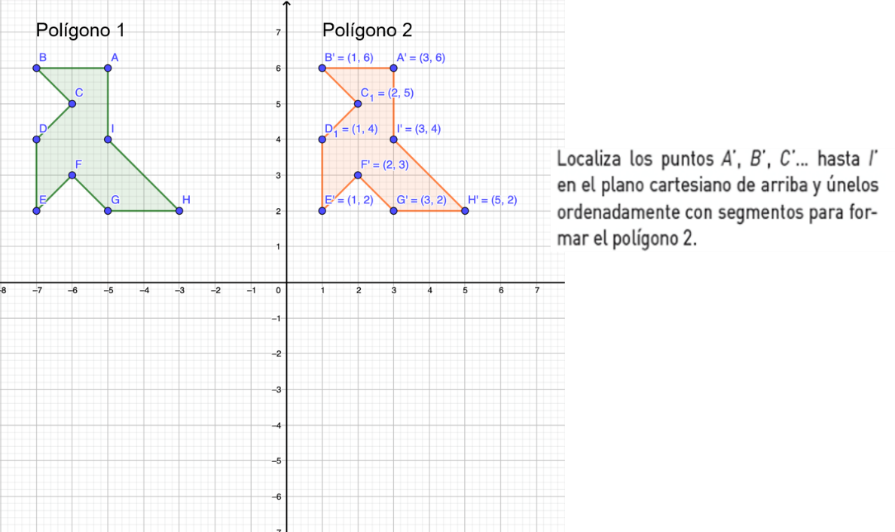
Si tú respuesta fue afirmativa quiere decir que lo que hiciste fue trasladarlo. Ya que el polígono 2 sigue conservando la medida de sus lados, la medida de sus ángulos, su tamaño y su forma.
Ahora traslada al segundo polígono 7 lugares hacia abajo.
Para tener las nuevas coordenadas del vértice Abi prima.
Observa bien, el valor de la ordenada de la coordenada A prima era 6 positivo y se pide que se mueva 7 hacia abajo,

por lo que el resultado será 1 negativo. Al valor de la abscisa no le haces nada, se queda tal cual.
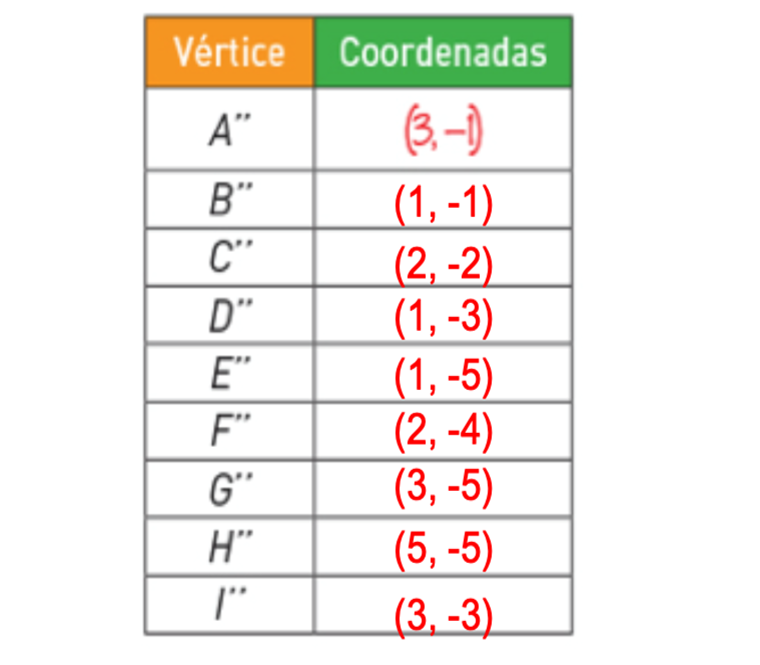
Haz lo mismo con todas las coordenadas. Recuerda que la ordenada corresponde a los valores de y. Por lo que, para el vértice Abi prima las coordenadas ahora serían, 3 positivo y 1 negativo.
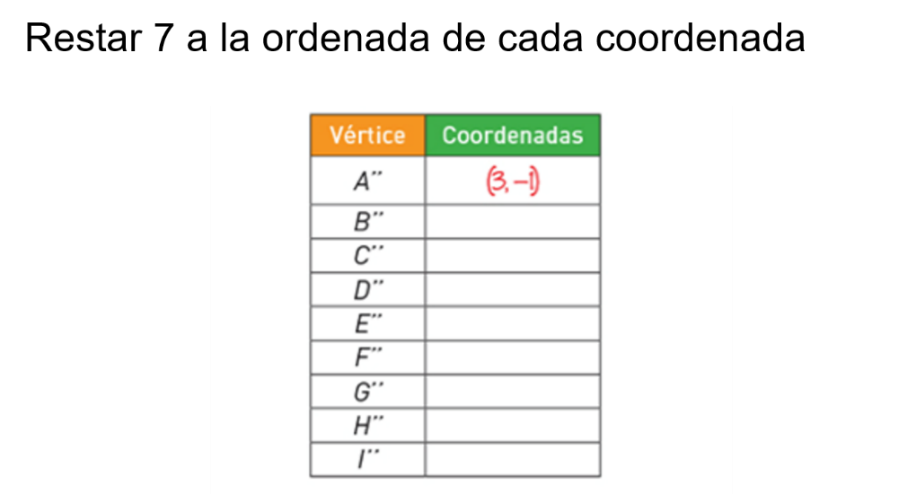
Observa si llegaste al mismo resultado.
Ahora, localiza los puntos Abi prima, Bbi prima, Cbi prima…hasta Ibi prima, en el plano cartesiano y únelos ordenadamente con segmentos para formar el polígono 3. ¿Cómo fue el polígono que formaste? Compara lo que realizaste.
Si comparas al polígono 2 con el nuevo polígono formado que es el 3, ¿Qué puedes determinar? Efectivamente que el polígono 3, no giró ni cambió de tamaño, solo se traslada dentro de un plano.
Y al igual que cuando formaron el polígono 2, sigue conservando la medida de sus lados, la medida de sus ángulos, su tamaño, y su forma, las cuales son propiedades de la traslación de figuras.
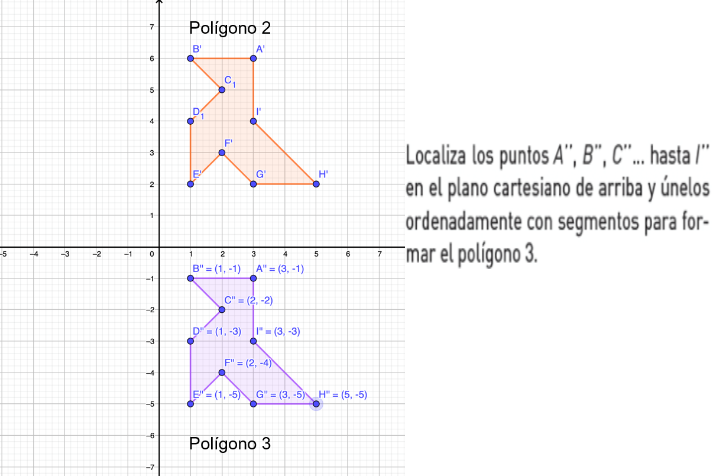
Recuerda las preguntas del inicio. ¿Conoces la palabra traslación?
Con lo que has visto hasta ahora, tienes una idea más clara de lo que esto significa. Ahora bien, quizás en este momento podrías imaginar más situaciones, ¿Dónde utilizas la traslación en tu vida cotidiana?
Si reflexionas, encontrarás una gran variedad de ejemplos de traslación en tu vida cotidiana; en la arquitectura, puedes encontrar objetos donde se ve reflejado este tema, en los puentes, monumentos, edificios, casas, etcétera; en el arte, al hacer combinaciones en el juego de figuras; en los animales, al realizar diversos movimientos para trasladarse.
Situación 3
Un maestro de matemáticas se puso como reto construir diversos diseños con sus alumnas y alumnos de secundaria.
El primer diseño que hicieron fue trasladar un triángulo, en diferentes direcciones para formar una figura más grande sólo con triángulos.
Irás construyendo y comparando, lo que el maestro hizo con sus alumnas y alumnos, utilizarás lápiz, papel, y de tu juego de geometría el compás y una regla.
Comienza construyendo un triángulo equilátero.
¿Qué característica tienen los triángulos equiláteros? Todos sus lados son iguales. Apóyate con el compás para construirlo.
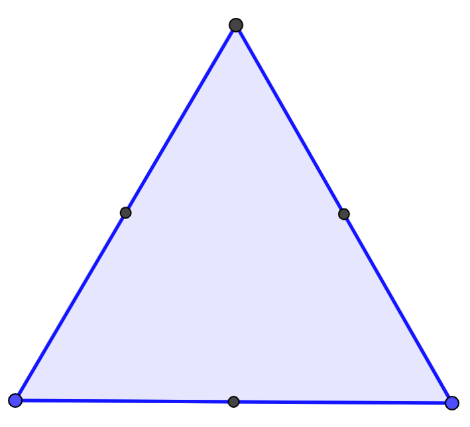
Una vez que tengas construido tu triángulo equilátero, busca el punto medio de cada uno de sus lados.
Posteriormente conecta los puntos medios con segmentos y así comenzarás a formar la primera figura.
Lo que harás ahora es comenzar a trasladar, la figura en diferentes direcciones.

Recuerda que para trasladar debes tener en cuenta las propiedades de traslación que aprendiste en el inicio.
La directriz y la longitud; la primera te indicará hacia donde moverás el triángulo y la segunda la distancia que va a recorrer.
Comenzarás trasladando el triángulo 4 unidades hacia la derecha.
Recuerda que todos los vértices se mueven en la misma dirección, así como la misma distancia.
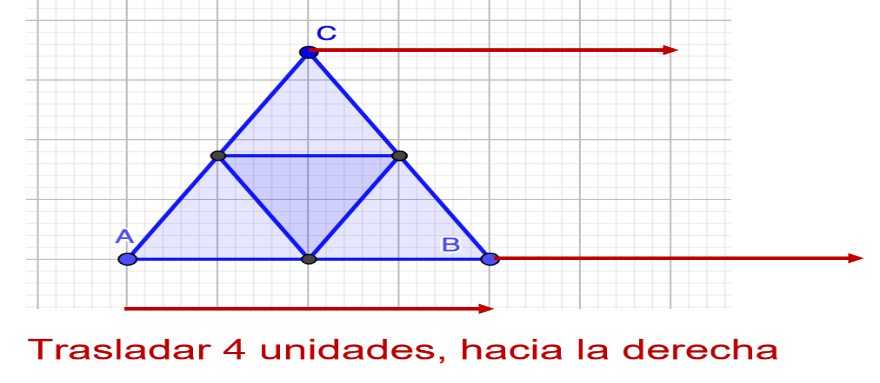
Cómo puedes observar la nueva figura formada se obtuvo trasladando el triángulo ABC 4 unidades hacia la derecha y obtuvimos el triángulo A prima, B prima y C prima.
Como te puedes dar cuenta el vértice A prima del nuevo triángulo coincide con el vértice B de la figura inicial.
Ahora realiza lo mismo solo que en diferente dirección, es decir, trasladarás el triángulo A prima, B prima y C prima, 4 unidades hacia arriba y luego 2 unidades hacia la izquierda.
Siempre debes recordar que todos los vértices se mueven en la misma dirección y distancia.
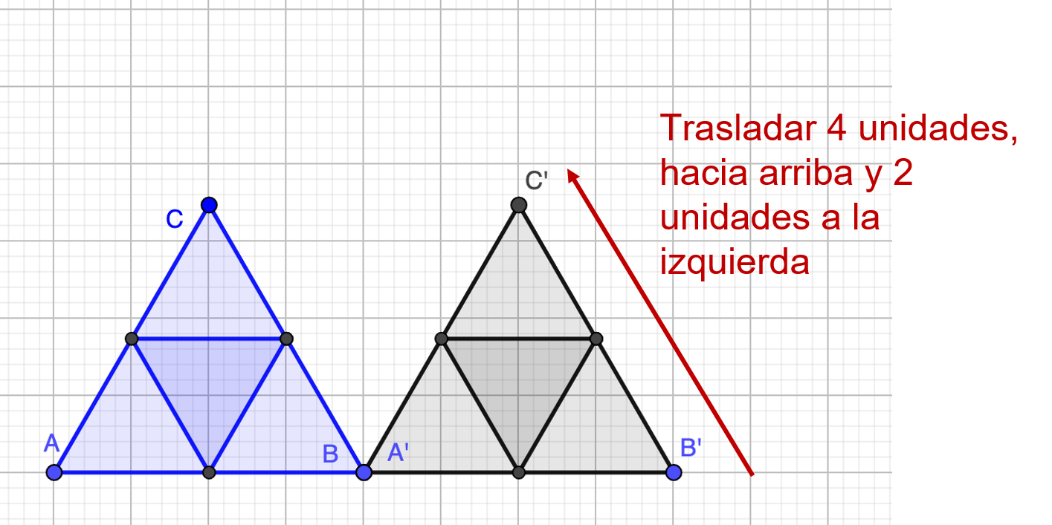
¿Cómo te quedó tu figura? ¿Lograste trasladarla?
Recuerda que el triángulo que se formará ahora será el triángulo Abi prima, Bbi prima y Cbi prima.
Compara las figuras: cómo puedes darte cuenta, el triángulo mayor se forma con la traslación de figuras, cada triángulo que fue trasladado, sigue conservando la medida de sus ángulos, la medida de sus lados, su tamaño y su forma.
Ahora bien, lo que estás haciendo. ¿Se va pareciendo a lo que el maestro realizó con sus alumnos?
Observa los trabajos de tus compañeros de secundaria.
Las alumnas y los alumnos del maestro de matemáticas lograron hacer figuras realmente increíbles.
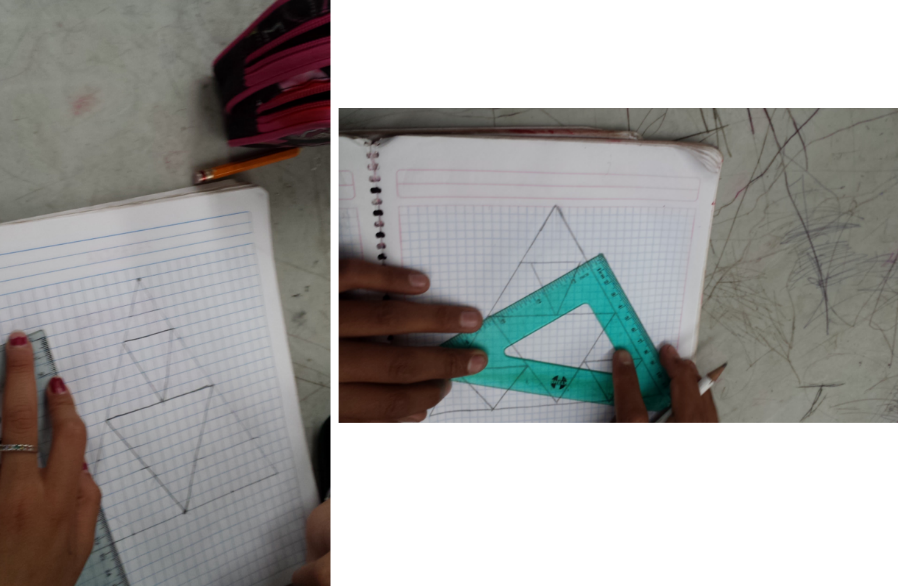
Solamente siguieron los pasos que acabas de hacer.

Para continuar con esta actividad, construye un triángulo equilátero de 5 mm por lado, y repite el proceso anterior varias veces alternando los movimientos a la derecha y a la izquierda de la manera en que se presenta a continuación.
Podrás darte cuenta de que existe un desplazamiento de cada punto entre las figuras geométricas. Realmente te vas a sorprender, cuando veas lo pueden llegar a formar.
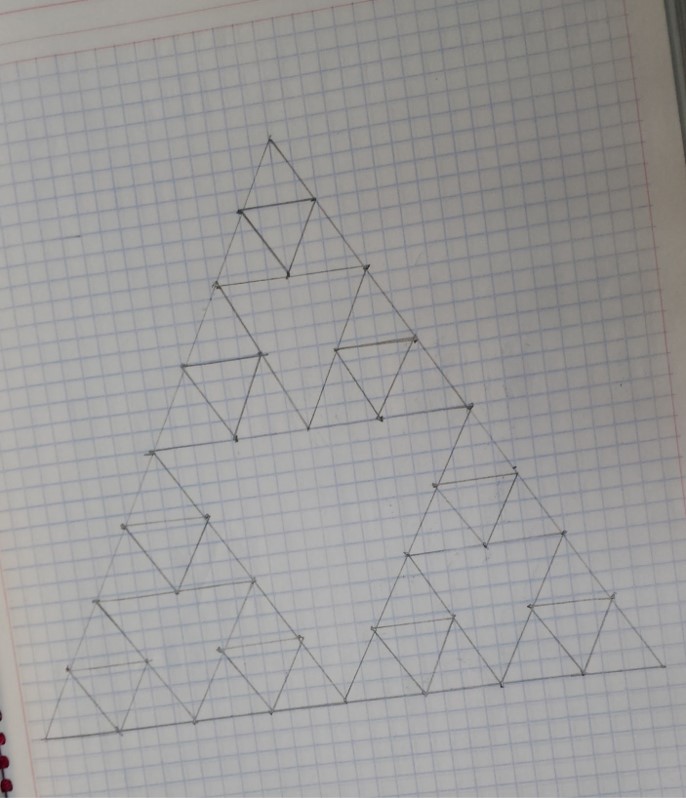
Una vez que lo tengas, ilumina los triángulos.

Te imaginas ¿hasta dónde podrías seguir trasladando el triángulo en el plano?
Cuando lo tengas, podrías compartirlo con tu familia y explicarles cómo lo hiciste y quizás más adelante, mostrárselo a sus compañeros y maestros.

Recuerda que en esta sesión estudiaste las propiedades de traslación de una figura.
La traslación tiene entre sus elementos la directriz y la longitud, conociste cual es el significado de traslación, el cual, es el movimiento de un cuerpo de un lugar hacia otro lugar.
Es importante que tomes en cuenta que la traslación conserva la medida de sus lados, la medida de sus ángulos, su tamaño, pero sobre todo su forma.
El reto de hoy:
Realiza dos retos:
El primero, es que busques en tu libro de texto de Matemáticas de tercer grado, problemas y ejercicios similares a los que estudiaste hoy, para que los resuelvas y practiques lo que aprendiste.
El segundo reto, es que pienses un tema que está muy relacionado con el que acabas de aprender. Una pista que te puede ser de ayuda, es que tiene que ver con los movimientos de la tierra.
¿Ya sabes qué tema?
Bien, con esto trabajarás la siguiente ocasión.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: