Propiedades de rotación de una figura
Propiedades de rotación de una figura
Aprendizaje esperado: explica el tipo de transformación (reflexión, rotación o traslación) que se aplica a una figura para obtener la figura transformada. Identifica las propiedades que se conservan.
Énfasis: analizar las propiedades de rotación de figuras.
¿Qué vamos a aprender?
Trabajarás con propiedades de traslación, las cuales te permiten mover una figura sin que esta cambie de forma, ni de tamaño, es decir, conservando la medida de sus lados y las medidas de sus ángulos.
Conocerás las propiedades de rotación en una figura, para que puedas llegar a entender más sobre el concepto.
¿Qué hacemos?
Antonio es un excelente alumno de una secundaria rural del estado de Oaxaca, después de asistir a la escuela como todos los días ayuda a su mamá a cuidar sus animales, ya que, entre chivos, borregos, toros y demás, la mamá no puede con todo. En una ocasión, le agarró la noche camino a su casa, en ese momento Antonio se preguntó ¿cómo se produce el ciclo del día y la noche?
Al día siguiente en la escuela, le pregunta a su maestro, cómo se da este fenómeno.
El maestro le contesta que es un fenómeno natural que tiene lugar en la Tierra, ya que los planetas del sistema solar están en constante movimiento girando alrededor del sol, todos los planetas incluyendo a la tierra giran sobre su propio eje y gracias a ese movimiento se hacen el día y la noche en la Tierra.
El maestro le muestra a Antonio una recreación de ese movimiento.
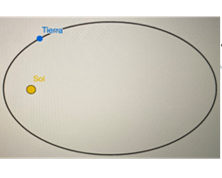
Observa como lo hizo:
- Movimientos de la tierra-rotación
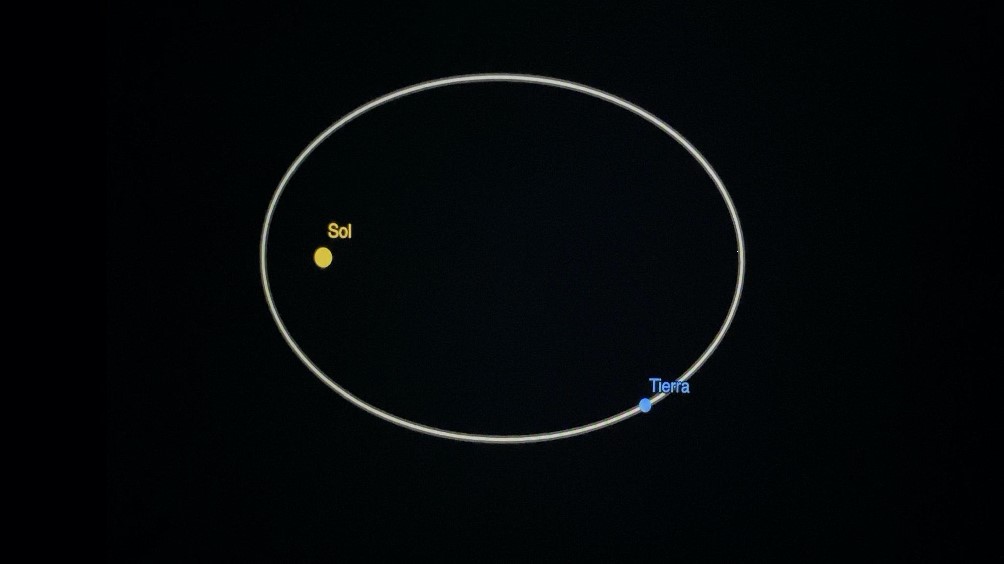
“Mira Antonio como puedes observar, el día y la noche se da por un fenómeno natural, la posición del sol en el sistema solar es fija, la tierra es la que gira alrededor del sol, y el tiempo para que esto suceda es de un año.
Al mismo tiempo que va girando alrededor del sol, está girando sobre su propio eje, y para dar un giro completo tarda 24 horas, a este movimiento se le llama rotación.
Solo una parte de la Tierra está de cara al sol en un momento determinado, es cuando está de día, mientras que la parte contraria es de noche. Gracias al movimiento de rotación, hace que cause el día y la noche en la Tierra.”
Acabas de aprender el movimiento que la tierra hace sobre su propio eje, a lo cual llamamos rotación.
La rotación, es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original.
Una rotación se determina por tres elementos:

- Un ángulo. Que determina la amplitud de la rotación.
- Un punto. Llamado centro de rotación.
- Un sentido de rotación. Que puede ser en el mismo sentido de las manecillas del reloj o en sentido contrario.
Conociste lo que significa la rotación y cuales sus propiedades. podrías decir, ¿dónde utilizas la rotación en la vida cotidiana?
Escribe en tu cuaderno dos ejemplos, donde consideres que usan la rotación.
Es importante escribir lo primero que se te venga a la mente, ya conociste un ejemplo con el caso de Antonio.
Otros ejemplos pueden ser:
Un rehilete de un niño al moverse con el aire.

Las llantas de un automóvil cuando va en movimiento.

La hélice de un helicóptero

Pero, ¿cómo se podría rotar el siguiente triangulo 90º en sentido contrario a las manecillas del reloj?
En tu cuaderno traza un plano cartesiano, utiliza solo el primer cuadrante, una vez que lo tengas, construye el triángulo como se muestra a continuación:
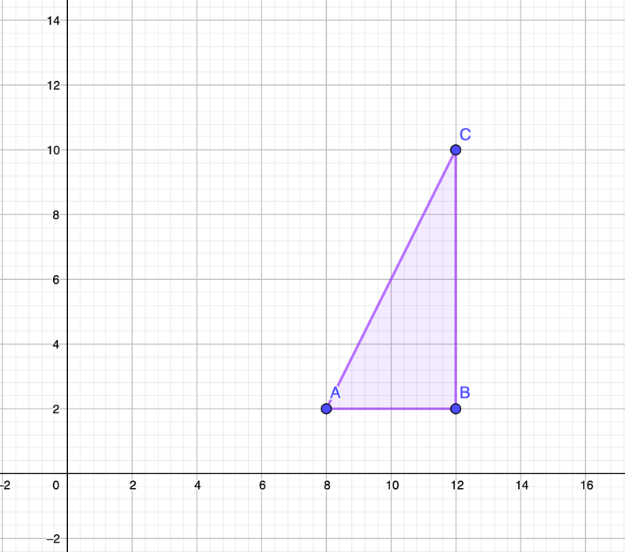
Primero debes observar cuales son las coordenadas de cada vértice que forman al triángulo. Recuerda que para ubicar cada vértice en el plano cartesiano tienes que la intersección entre el valor de x con el valor de y.
Efectivamente, las coordenadas del vértice A son 8 positivo y 2 positivo, las coordenadas del vértice B son 12 positivo y 2 positivo, y las del punto C son 12 positivo y 10 positivo. Recuerda que, al estar trabajando el primer cuadrante del plano cartesiano, todos los valores tanto de las abscisas como de las ordenadas serán positivos.
Ahora bien, comienza por rotar la figura, respecto al punto A, 90º en sentido contrario a las manecillas del reloj.
¿Hacia dónde girará el triángulo?
Realiza la rotación.
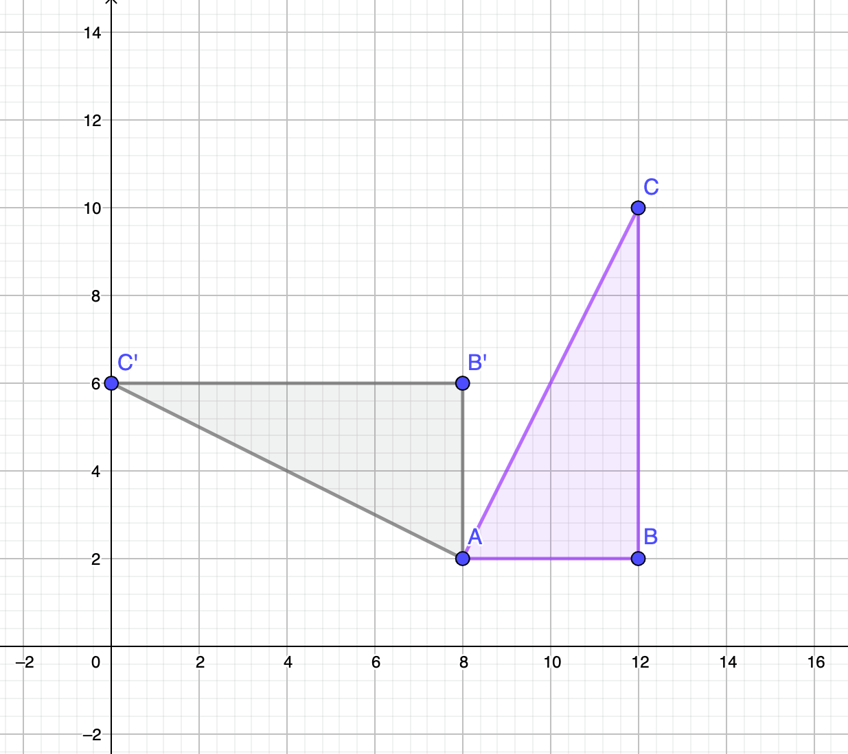
Cómo puedes observar la figura hizo un giro de 90º grados en sentido contrario a las manecillas del reloj, pero el triángulo sigue siendo el mismo, conserva la medida de sus lados, la medida de sus ángulos y tiene el mismo tamaño.
Al hacer la rotación solo cambió de posición. Observa cuáles son sus nuevas coordenadas, para el vértice A prima conserva la posición ya que ese fue el punto que utilizaste para rotar, sus coordenadas son 8 positivo y 2 positivo, para el vértice B prima ahora son 8 positivo y 6 positivo, y para el vértice C prima, sus coordenadas son cero y 6 positivo.
Ahora rota el triángulo de su posición actual, 105º grados en sentido contrario a las manecillas del reloj, de igual manera tomando al vértice A prima como centro de rotación.
Piensa ¿cómo se vería la figura?
¿Se parece a la que construiste?
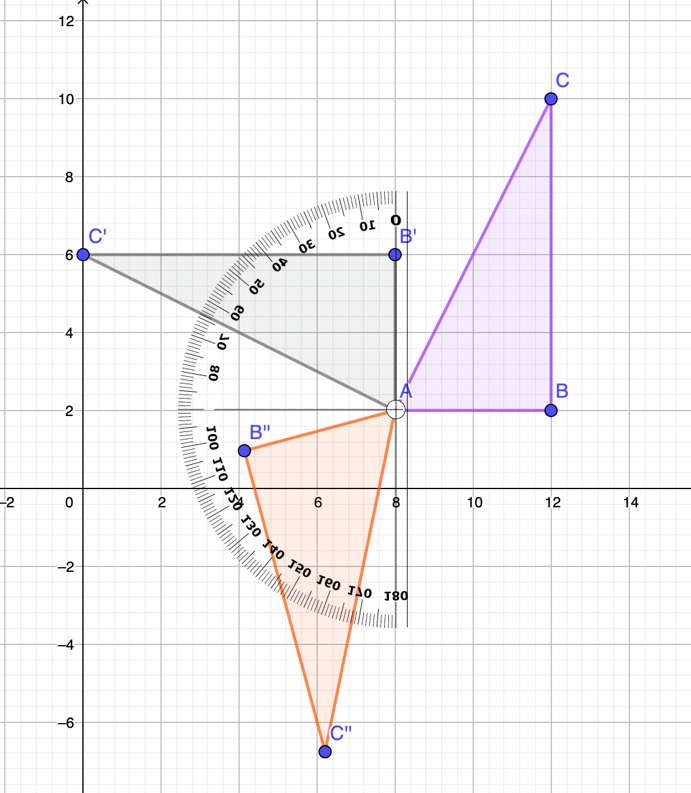
Cómo puedes observar, cuando haces la rotación, debes tener en cuenta sus propiedades, es decir, el ángulo el cual determina la amplitud de la rotación, para este caso fue de 105º grados, el centro de la rotación, que para esta figura fue el vértice A prima, así como el sentido hacia donde será la rotación, para este ejercicio fue en sentido contrario a las manecillas del reloj.
Realiza la siguiente actividad.
Vuelve a rotar el triángulo, pero ahora 60º grados, en sentido contrario a las manecillas del reloj, tomando como posición al punto Abi prima.
A continuación, observa algunas situaciones que resolverás para conocer más de este tema.
Situación 1.
Mi prima Yasmín que le gusta viajar por el mundo, visitó la plaza de los milagros en Pisa, Italia, para conocer una de las 7 maravillas del mundo moderno, se refiere a la Torre inclinada de Pisa.
¿Sabías que la Torre de Pisa se comenzó a construir en el año de 1173, y que cuando el tercer aro o círculo fue construido, el edificio comenzó a inclinarse debido a la estructura del peso en las bases?

Esta fue la razón principal por la cual interrumpieron la construcción y luego continuaron en el año de 1275. Esta torre mide 55.86 m de altura.
La Torre de Pisa tiene 3.97 grados de inclinación.
¿Podrías realizar una simulación de la inclinación de esta torre? ¿cómo se te ocurre realizarlo? Trata de plasmarlo en tu cuaderno. Puedes utilizar el plano cartesiano, para hacer la simulación.
Los pasos para hacer la simulación son los siguientes:
Para comenzar traza un plano cartesiano y dibuja un rectángulo lo más parecido a la imagen, esta será tu torre de Pisa, el eje de las abscisas simulará el suelo, la parte que está por debajo del eje, serán los cimientos de la torre.
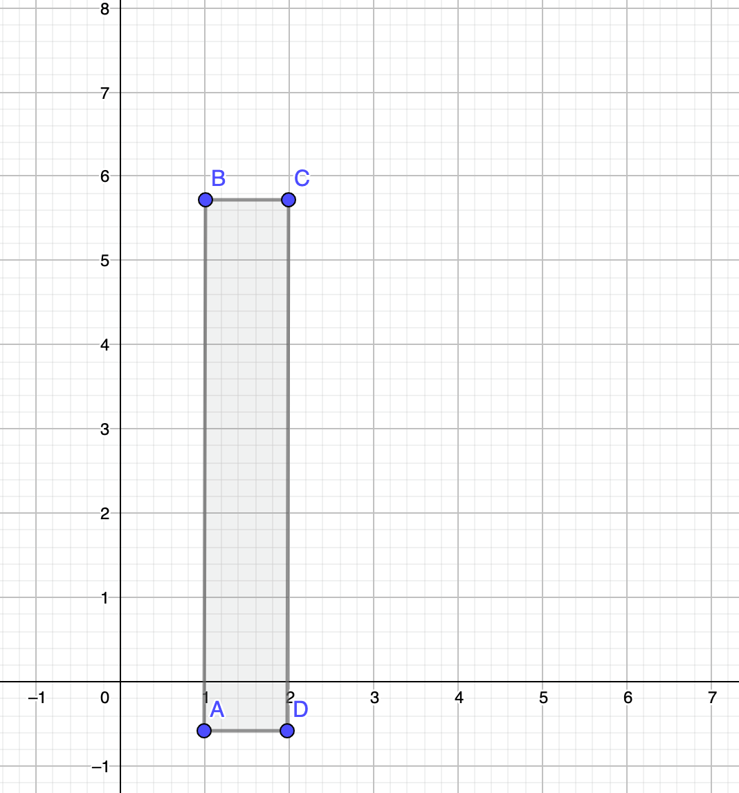
¿Recuerdas hacia donde se encuentra la inclinación de la torre?
Efectivamente, la inclinación va en sentido horario, es decir, en el mismo sentido que giran las manecillas del reloj.
Ahora bien, sabes que la torre de Pisa tiene una inclinación de 3.97 grados. Toma como centro de rotación al vértice D.
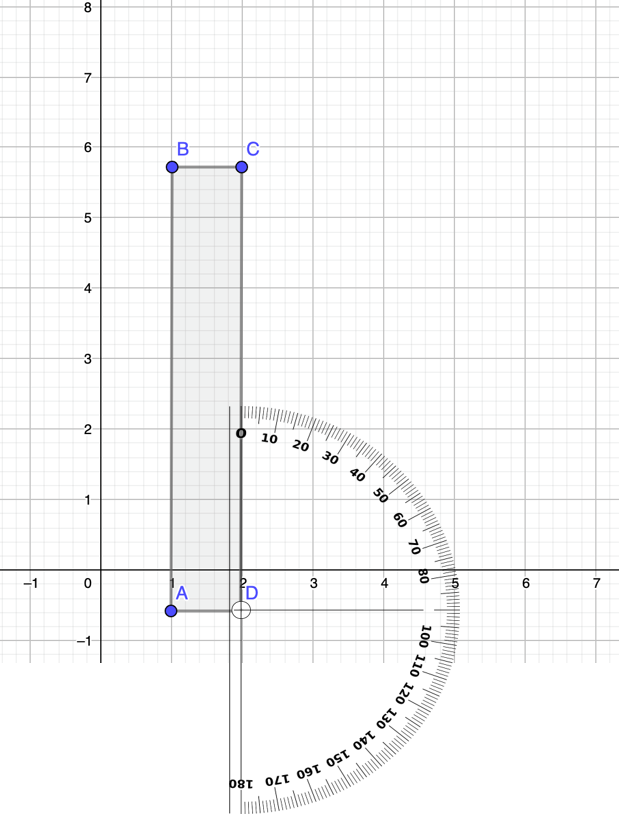
Ahora rota cada uno de los vértices de la figura, 3.97 grados. Después une los vértices en el mismo orden. Y listo tu simulación está hecha.
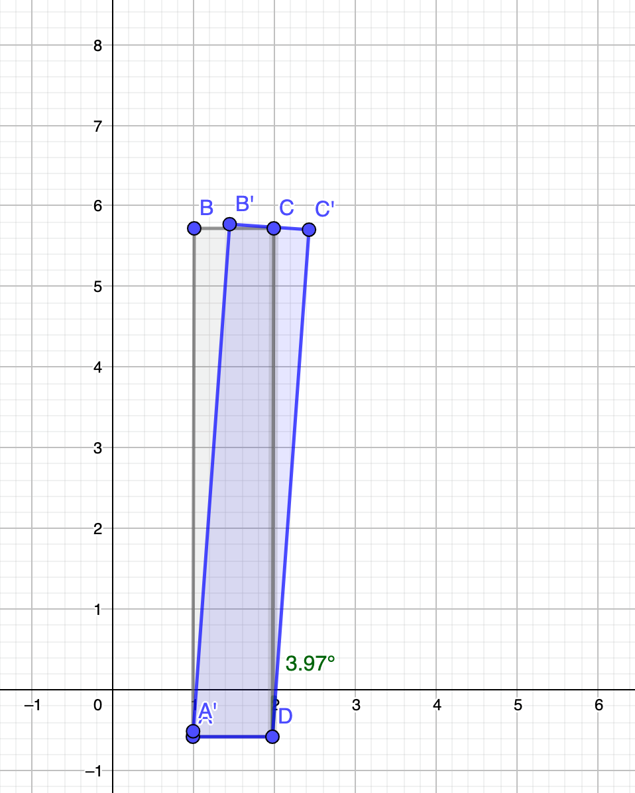
Esa es la inclinación que ha sufrido la Torre de Pisa.
Realiza lo siguiente: Supón que, con el paso del tiempo, la torre de Pisa, se inclinará dos grados más, ¿podrías hacer la simulación y determinar cómo se vería?
Realízalo y compártelo con tu familia y explícales cómo lo hiciste.
Un dato interesante es que la torre de Pisa no es la más inclinada del mundo.
Investiga cual es la torre más inclinada del mundo y realiza la rotación de la figura.
Recuerda que en la rotación la figura se mueve, alrededor de un punto, pero manteniendo la forma y el tamaño original.
Situación 2.
Don Roberto es un albañil, y lo contrataron para poner el piso del palacio municipal de su pueblo. Le recomendaron poner adoquines con dos figuras diferentes. El decidió utilizar hexágonos, pero le falta otra figura para poder rellenar el plano.
¿Qué otra figura podría utilizar?
¿Podría escoger cuadrados?
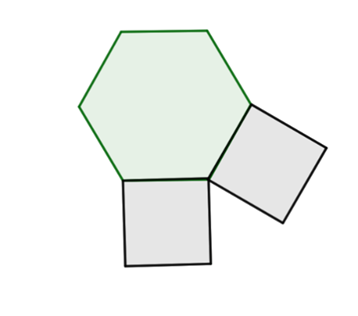
Don Roberto, no podría escoger los cuadrados porque tendría que utilizar una figura más para recubrir el plano. Después de un tiempo se dio cuenta que las dos figuras a utilizar eran hexágonos regulares y triángulos equiláteros. Si don Roberto coloca el primer triángulo en la parte superior del hexágono, y desea que el giro sea a la izquierda.
¿Cuántos grados tendría que rotar al triángulo KLM?, ¿cuál sería el sentido? si se toma como centro, el vértice K.
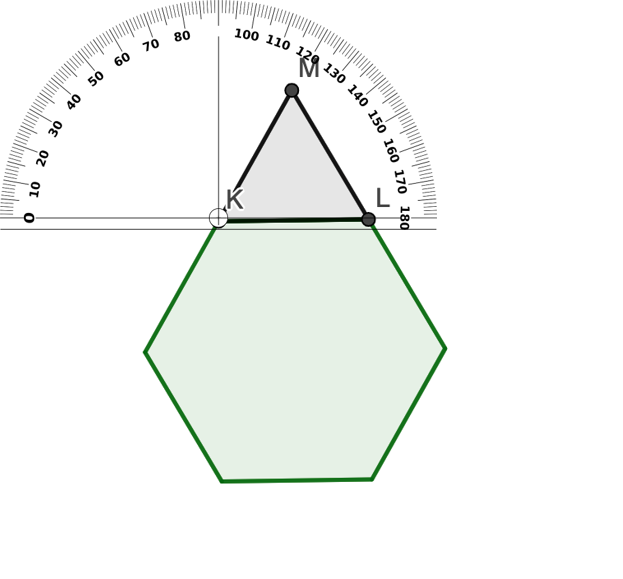
El triángulo tendría que rotar 180º grados. Y el sentido sería contrario a las manecillas del reloj.
En tu cuaderno traza el hexágono y el triángulo equilátero en la parte superior, junto con la rotación que acabas de hacer, tal cual lo hizo don Roberto.
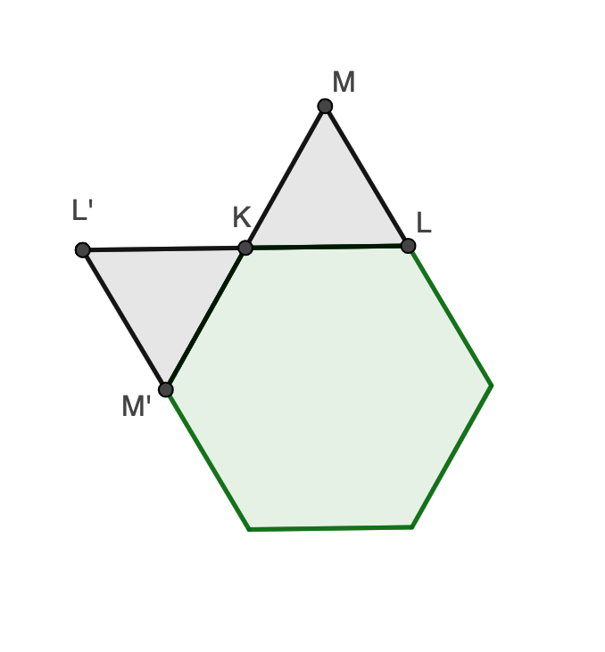
Ahora te toca trasladar el triángulo KLM, pero hacia el lado derecho.
¿Cuál sería el vértice que tomarías como centro de rotación?
¿Cuántos grados girará el triángulo?
¿Cuál es el sentido del giro?
En este caso el vértice que tomarías como centro de rotación sería el vértice L. El ángulo de rotación sería 180º grados, y en sentido horario, es decir, en sentido a las manecillas del reloj.
Una vez que tengas los vértices únelos en orden para que se vaya formando el nuevo triángulo equilátero, y así sucesivamente.
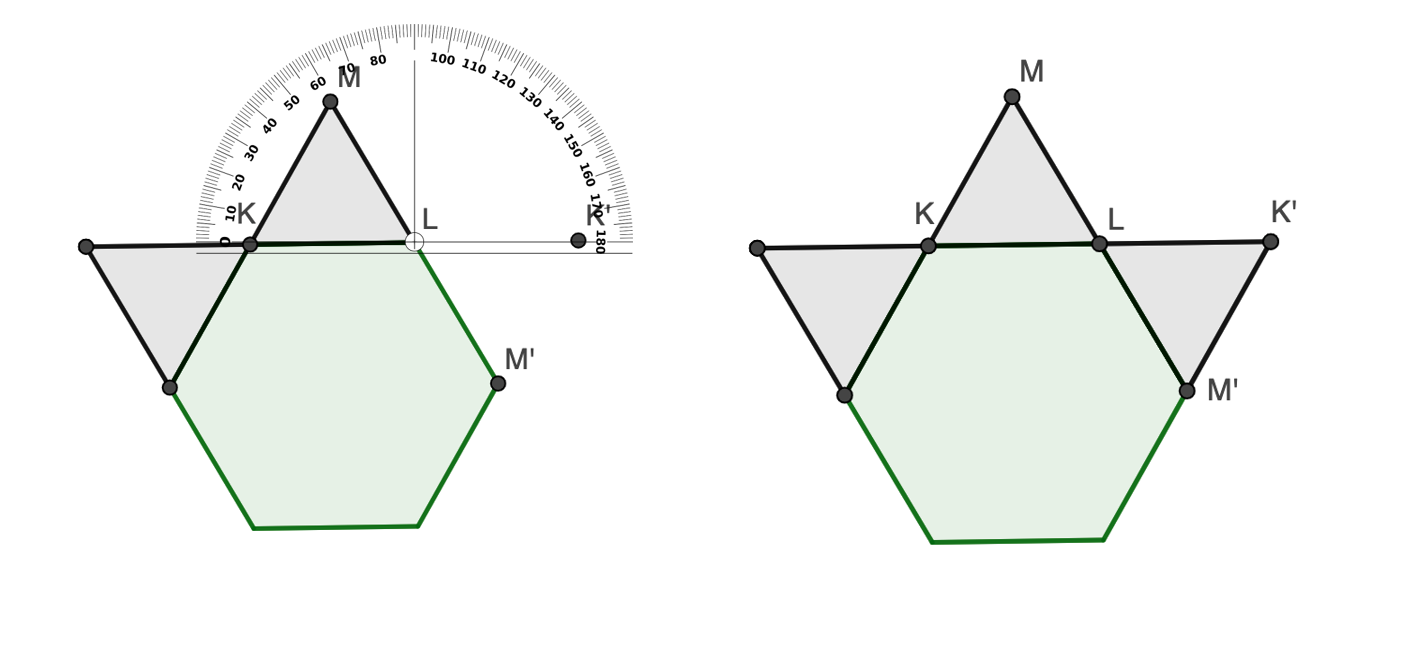
Descubre el plano para observar cómo le quedaría a don Roberto.
¿Cuántos triángulos equiláteros tendría que rotar alrededor de la figura?
Efectivamente son 6 triángulos los que tendrías que rotar alrededor de cada hexágono.
Para que te des una idea, así es como tendrías que ir llenando el plano.
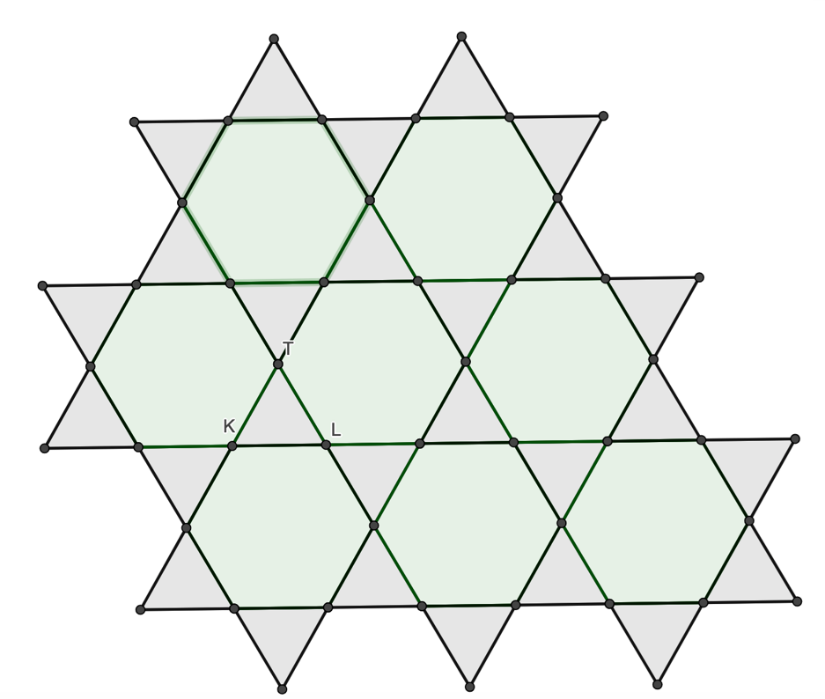
Una vez que lo termines no olvides compartirlo con tu familia, quizás hasta podrías explicarles cómo lo hiciste.
Observa la siguiente situación.
Situación 3
¿Recuerdas cuando José le ayudó a su papá a buscar la manera de acomodar figuras de un juego, que su papá jugaba?
Donde el juego consistía en ir acomodando figuras que van saliendo, de tal manera que no queden espacios entre ellas. Porque el objetivo del juego era ir formando líneas de manera horizontal.
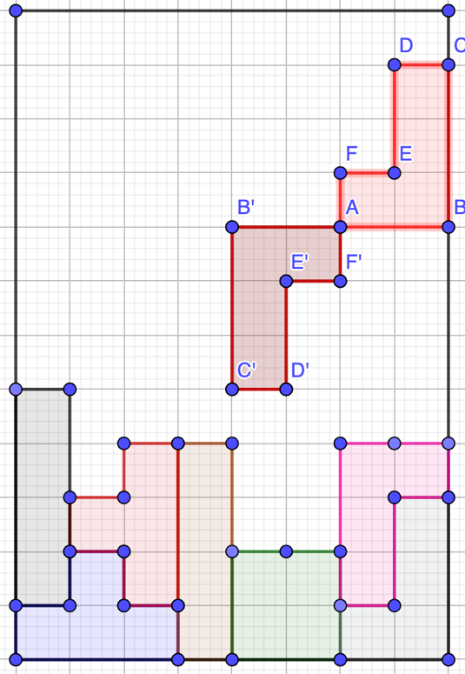
Si quisieras acomodar la siguiente figura: ¿Cómo le harías para acomodar el cuadrilátero, de tal manera que pudieras colocarla en la parte punteada?
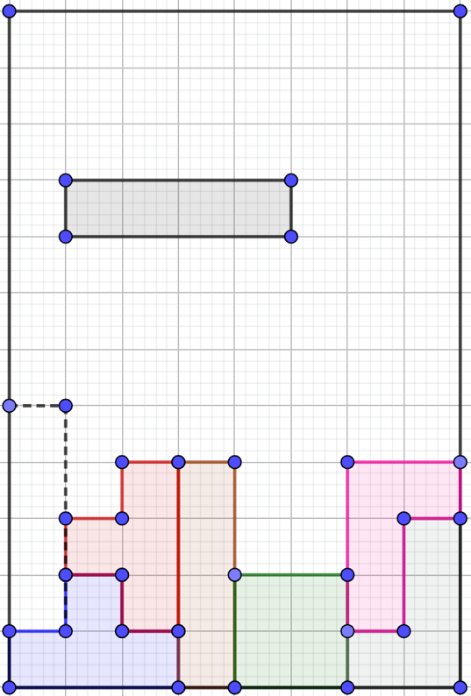
¿La harías rotar? ¿Hacia dónde sería el sentido de rotación? Debes poner en práctica lo aprendido para poder realizarlo.
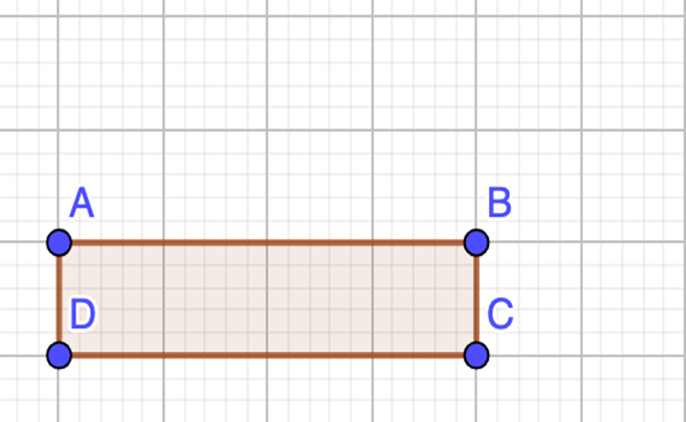
Observa: Tienes un cuadrilátero que lo nombrarás: el cuadrilátero ABCD.
Para dar respuesta a las preguntas anteriores, tienes que rotar al cuadrilátero, en el sentido contrario a las manecillas del reloj.
Debes rotarla 90º grados. Ahora bien, ¿qué vértice tomarías como eje de rotación?
El vértice que se toma como eje de rotación sería al D.
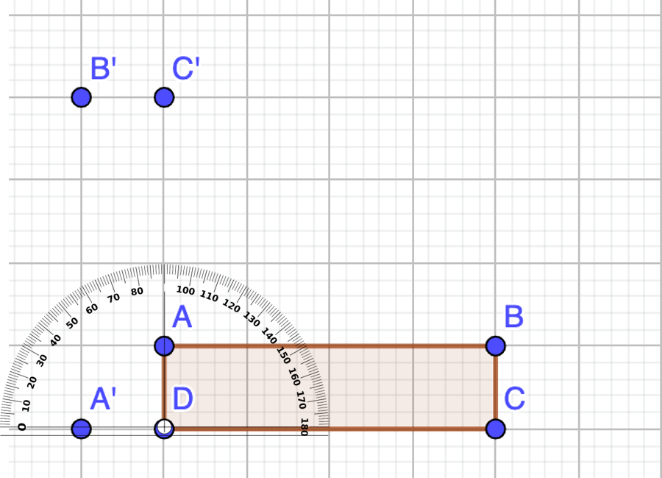
La figura está lista para ser colocada, solo la trasladarás 7 unidades hacia abajo.
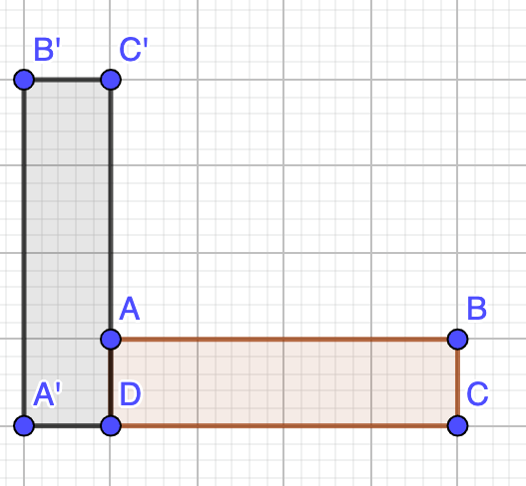
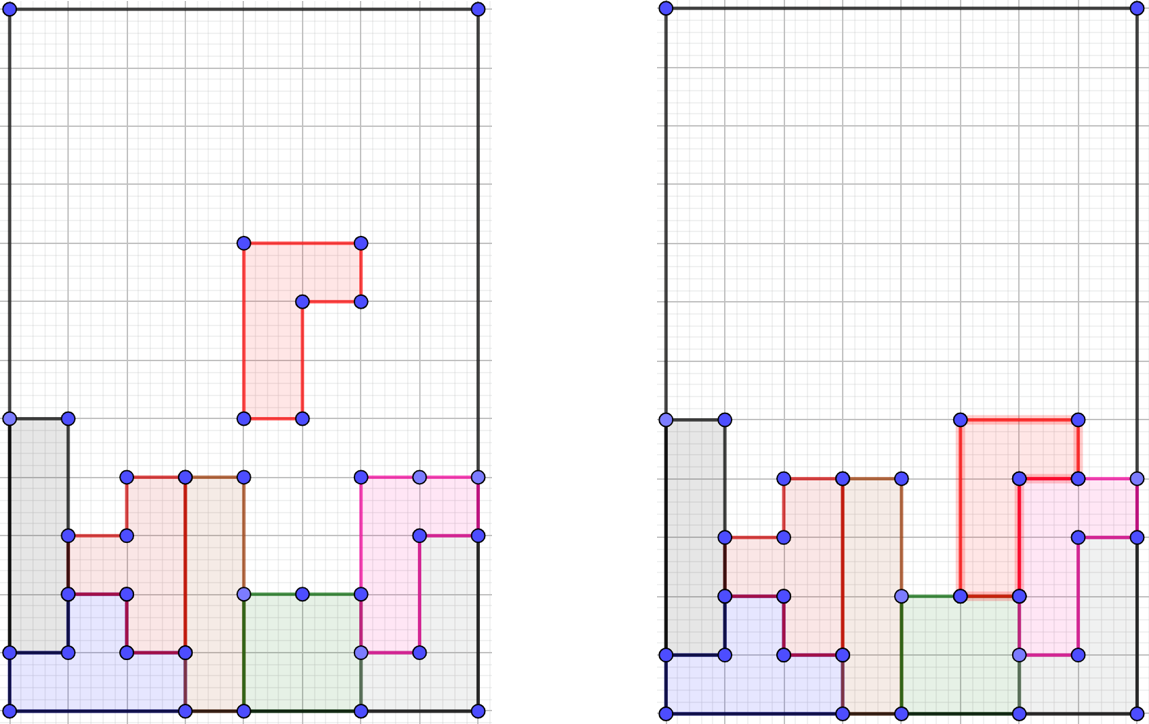
Coloca la siguiente figura:
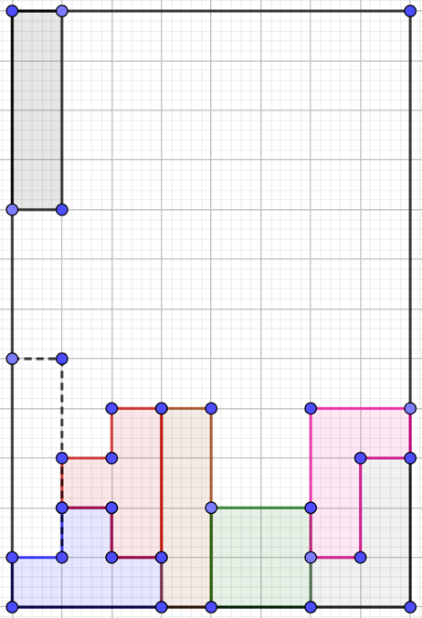
Piensa cuáles son los pasos a seguir, para colocarla en el lugar que se te indica.
¿Hacia dónde harías la rotación?
¿Cuántos grados rotarías la figura?
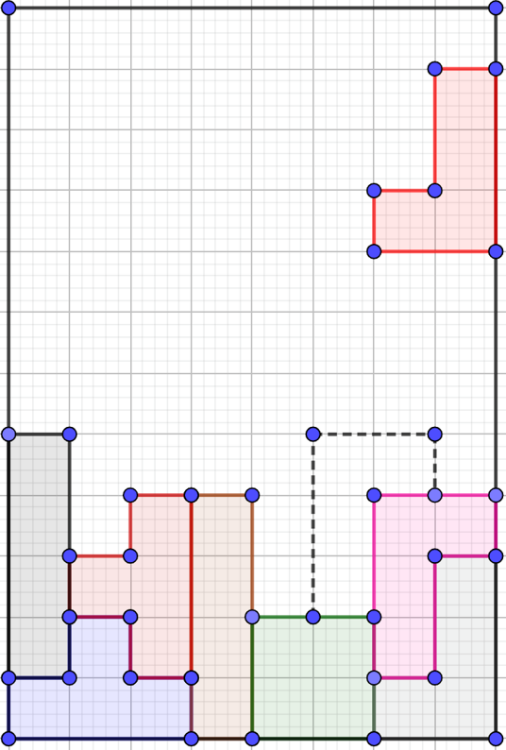
Se te recomienda que lo primero que hagas sea nombrar a la figura. Cuando tengas los nombres de los vértices, observa sobre qué punto harías la rotación.
Si realizas la rotación sobre el vértice B, ¿la figura quedaría lista solo para hacer la traslación hacia abajo?
¿Cuál sería el mejor punto para rotar?
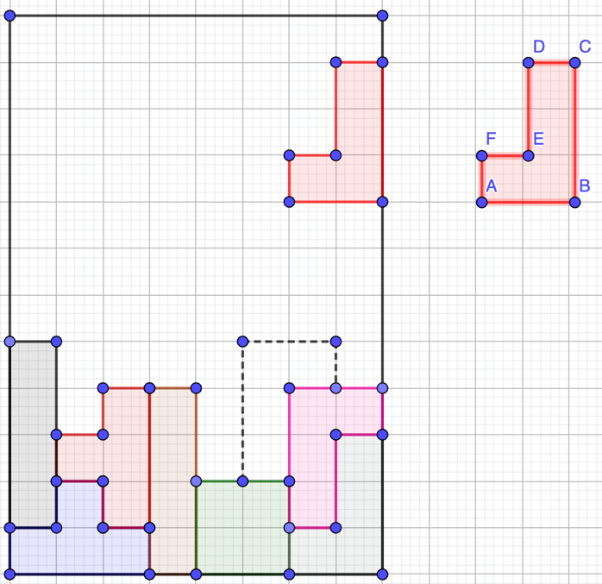
Rota por el vértice que desees, siempre y cuando todos los giros vayan hacia el mismo sentido.
El ejemplo será tomando como centro de rotación al vértice A. Ahora bien, la rotación sería en contra del sentido de las manecillas del reloj. Los grados que giraría la figura, tendría que ser de 180º grados.
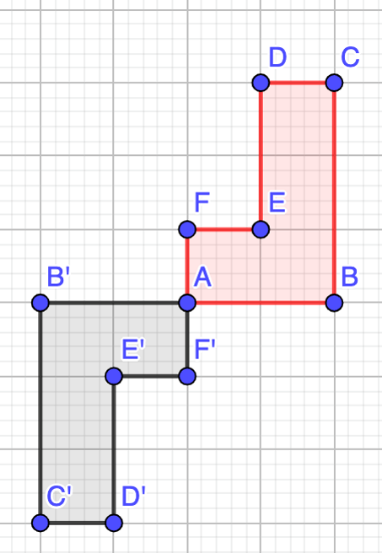
Por último, solo resta trasladar la figura una unidad hacia la derecha y 3 unidades hacia abajo.
Situación 4
Danaé es una alumna de tercer grado de secundaria, y va a presentar un examen muy importante para conseguir una beca y continuar con sus estudios, sin embargo, tiene dudas con algunos ejercicios relacionados con la rotación de figuras.
Podrías ayudarle a corroborar que las respuestas que ella está escogiendo son las correctas.
EJERCICIO 1
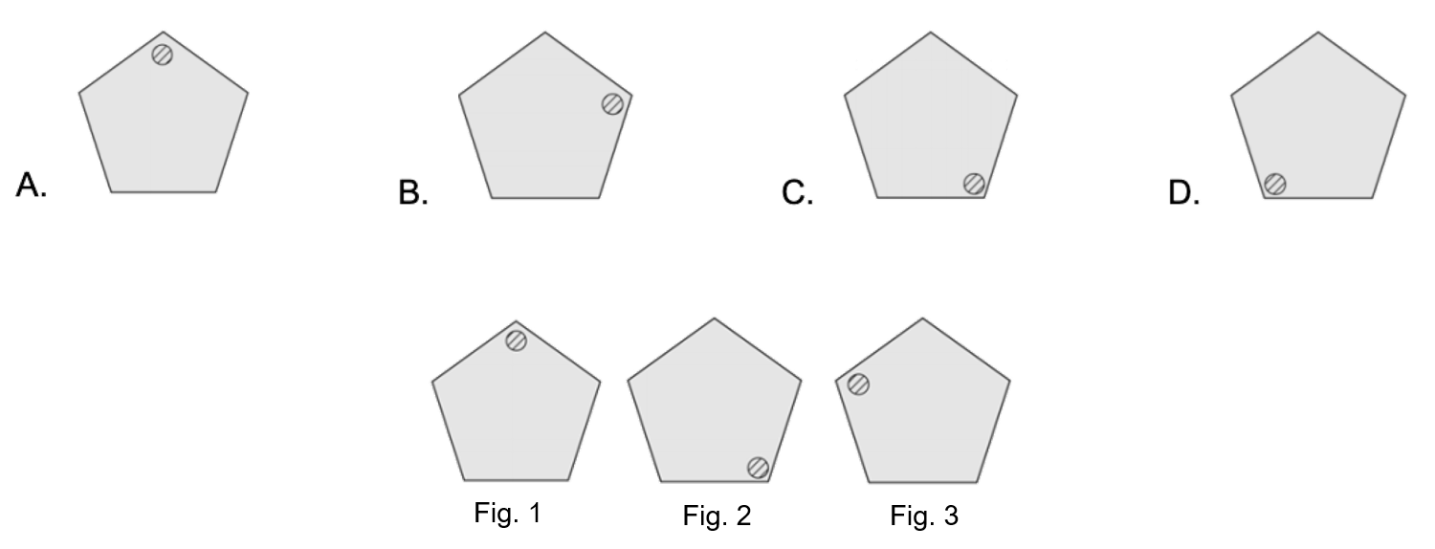
Observa las siguientes figuras, y determina, ¿cómo sería el pentágono que seguiría en la posición E?
¿Cuántos grados va rotando la figura en cada inciso?
¿Hacia dónde gira la figura?
Logras identificar ¿Cómo debe ser la siguiente figura que está buscando Danaé?, aquí lo interesante es cómo podrías argumentar tu respuesta, para explicársela a Danaé.
Construye la primera figura para contestar las preguntas del inicio.
Realiza lo siguiente:
Construye un pentágono para saber cómo sería el movimiento de rotación. Una vez que lo tengas, nómbrenlo como pentágono ABCDE.
Ahora bien, ¿Cuál sería el sentido de rotación para el pentágono?
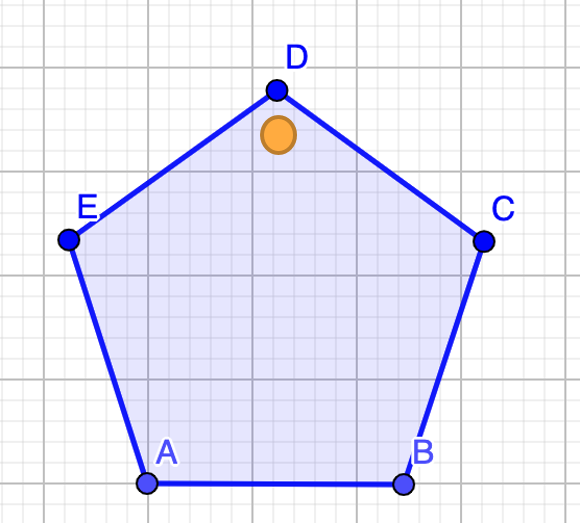
Sería en sentido horario, es decir, en el mismo sentido que giran las manecillas del reloj.
¿Qué vértice utilizarías para hacer rotar la figura?
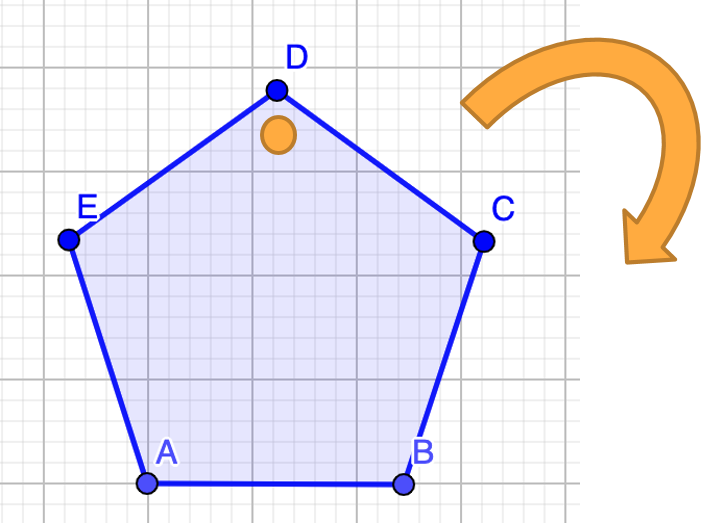
Para rotar el pentágono ABCDE tendrías que tomar como centro de rotación al vértice B.
Ahora bien, ¿Cuántos grados tendrías que rotar la figura?
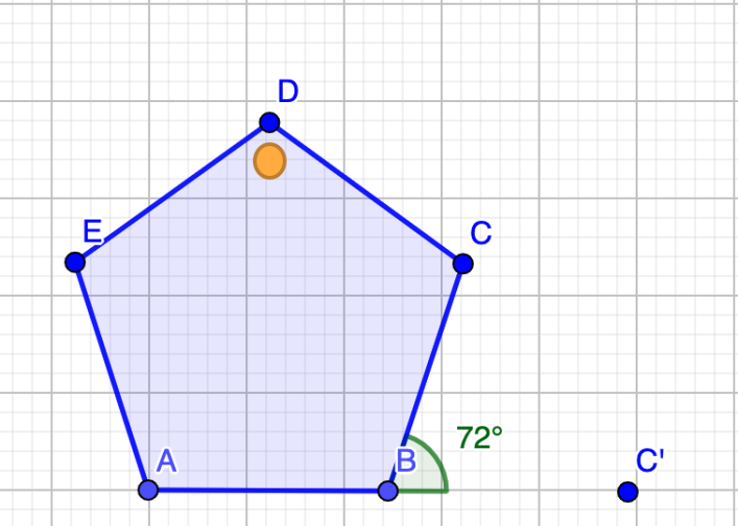
Si tomas como centro de rotación al vértice B, tendría que girar 72º grados.
Ahora lo único que resta por hacer es rotar todos los puntos y obtendrás el pentágono A prima, B prima, C prima, D Prima, E prima, que corresponde al pentágono del inciso B. Ya solo lo trasladarás tres unidades hacia la derecha.
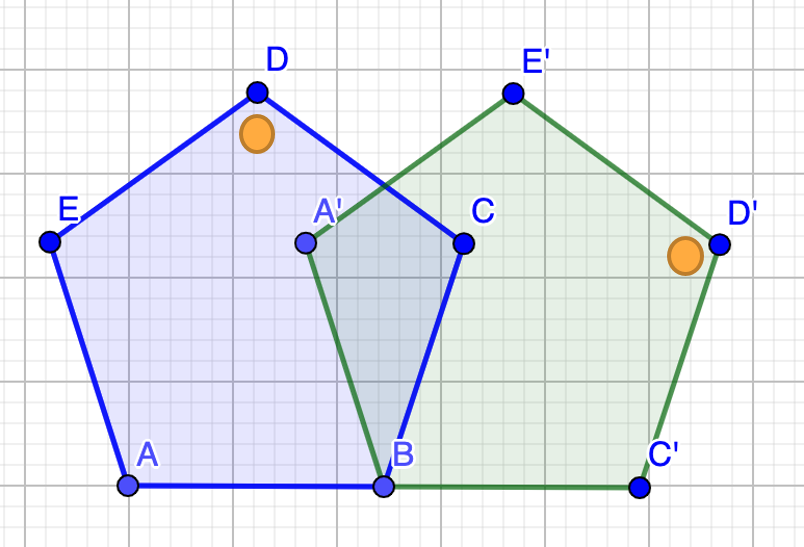
Lo que tendrías que hacer a continuación, es el mismo proceso para obtener los siguientes pentágonos.
Ahora sí podrías explicarle a Danaé, que el pentágono que sigue después del inciso D, sería la figura número 3.
¿Cuántos grados rotó en total el polígono? Piensa en tu respuesta.
Recuerda, que de la primera a la segunda figura rotó 72º grados, es decir, de la figura A a la B, y si me están solicitando hasta la letra E, entonces, ¿Cuántos grados giro en total?
El polígono original, en total rotó 288º grados.
EJERCICIO 2
Observa con atención la siguiente imagen, pon en práctica lo que hasta ahora sabes de la rotación de figuras, para ayudar a Danaé.
Cómo puedes darte cuenta, el modelo tiene un triángulo en la parte superior, en el centro un círculo, en la parte inferior un cuadrado sombreado y a la izquierda un cuadrado.
Selecciona la figura, que no sea exactamente igual al modelo.
Observa detenidamente cada uno de los incisos.
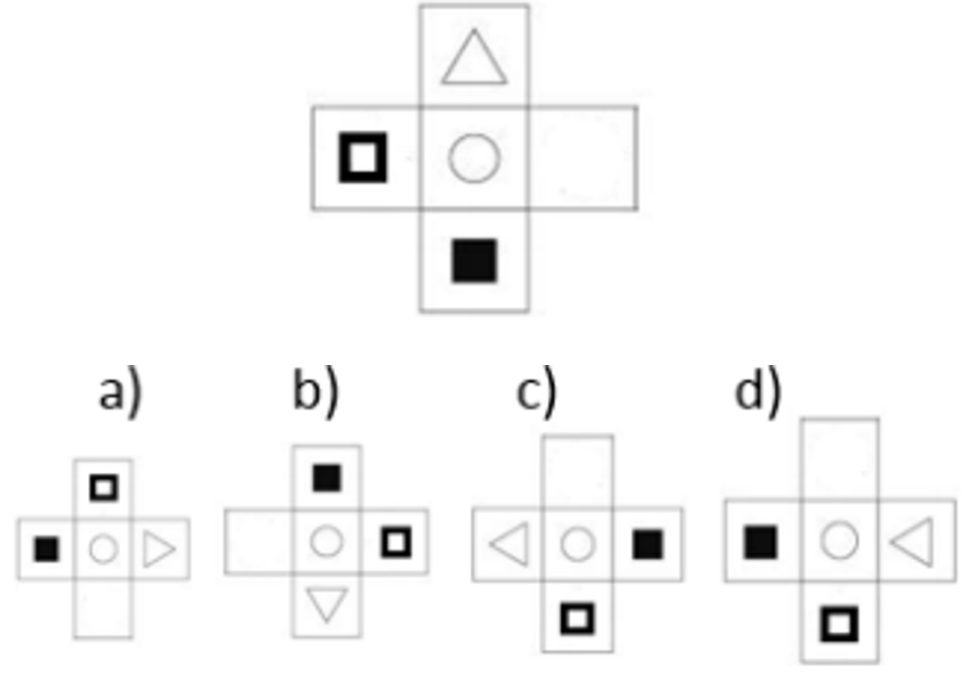
Como puedes darte cuenta la figura está rotando en cada uno de ellos.
Lograste identificar, ¿qué inciso no corresponde al modelo?
Al rotar la figura el inciso d) es el que no corresponde.
EJERCICIO 3
Observa el siguiente dado.
¿Cuál de las siguientes figuras corresponden a la anterior después de haberla girado 90º grados en sentido contrario a las manecillas del reloj?
Recuerda que lo primero es observar el dado detenidamente y analizar la posición de los números.
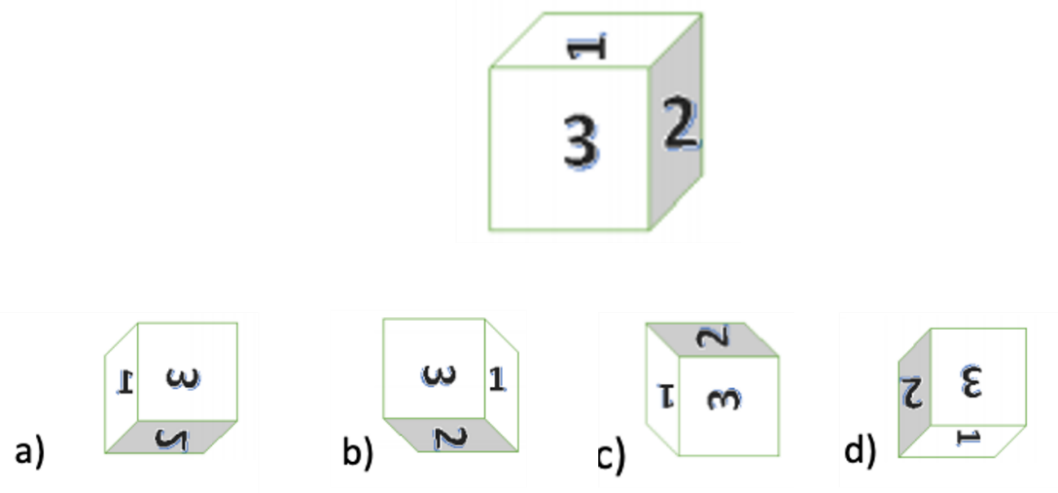
¿Cuál fue la estrategia que utilizaste, para llegar a la respuesta?
Danaé lo que hizo fue tomar como referencia un solo número, por ejemplo, ella tomó al número 2 e imaginó como sería la posición de ese número al girar el dado 90º grados a la izquierda. Posteriormente lo que hizo fue observar que los demás números también coincidieran después de que el dado haya rotado los 90º grados.
EJERICIO 4
En el siguiente ejercicio observa detenidamente la figura modelo.
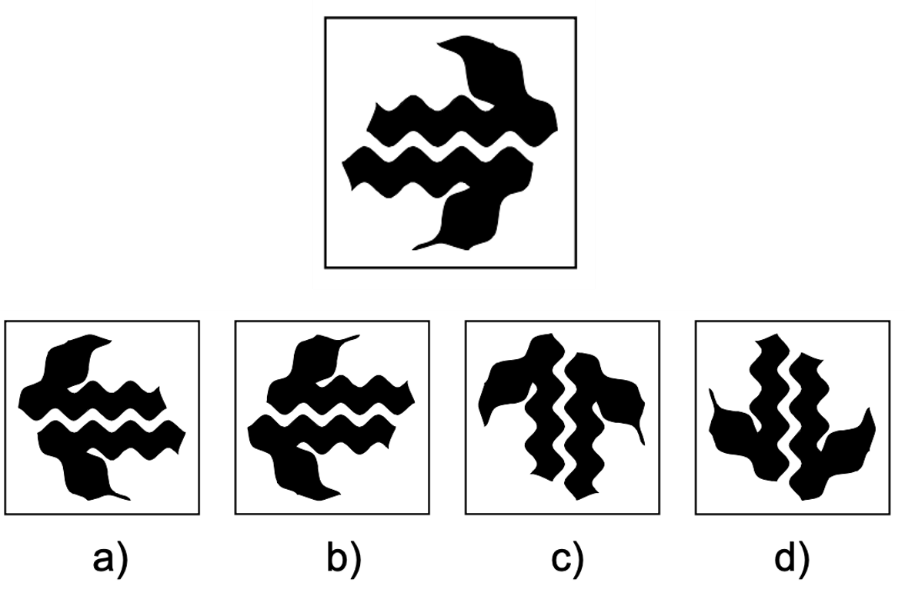
De las cuatro opciones al rotarlas ¿Qué figura no corresponde con las demás?
Una de las opciones de respuesta, no coincide con esta figura modelo y por lo tanto no es igual, ayuda a Danaé, a identificar cuál es la figura diferente.
¿Lograste identificarla?
¿Qué figura piensas que no corresponde con las demás?
Analiza cada una de las respuestas y observa detenidamente los detalles.
Comienza por el inciso d).
Si observas la figura modelo, puedes darte cuenta que en este inciso la figura sí coincide con el modelo, ya que lo único que está haciendo es rotar 90º grados en sentido horario.

Ahora bien, para el inciso c), si comparas la figura modelo con este inciso, la figura también coincide, solo que, en este caso, está rotando 90º grados en sentido contrario a las manecillas del reloj.

Compara la figura modelo, ahora con el inciso b).

¿Qué puedes observar en este inciso? ¿Hacia dónde está girando la figura? ¿Cuántos grados está rotando?
La figura está rotando 180º grados, en sentido contrario a las manecillas del reloj
Observa por último el inciso a). ¿Qué puedes observar en este inciso? ¿La figura está rotando?

En este inciso, por más que rotes a la figura, jamás coincidirá con la figura modelo, por lo tanto, esta es la respuesta que no coincide.
Recuerda lo que se mencionó al inicio, que la rotación es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original.
EJERCICIO 5
¿Qué figura no corresponde con las demás?
Observa detenidamente.
¿Podrías decir, hacia dónde están girando las figuras?
Las figuras A, B, C, y E son las correctas en la rotación del triángulo, la cuales van en sentido contrario a las manecillas del reloj, por lo tanto, la figura que no corresponde a esta rotación es la figura D.
Resuelve un último ejercicio de rotación de figuras, para ayudarle a Danaé.
Observa las siguientes figuras:
¿Qué figura no tiene relación con las demás?
Recuerda siempre imaginar cómo podrías ir rotando la figura.
Observa que todas las figuras son iguales; sin embargo, al girar las figuras en sentido horario o anti horario, todas podrían tomar la posición de la figura E, a excepción de la figura C. Debido a que esta se encuentra colocada de diferente manera.
Debes tener presente lo que aprendiste: “las propiedades de rotación de una figura”.
Las cuales tienen que ver con un ángulo, un punto y un sentido.
Un ángulo, porque es el que determina la amplitud de la rotación, un punto, ya que este será el centro de rotación y un sentido, que puede ser el mismo sentido de las manecillas del reloj o en sentido contrario.
Conociste cual es el significado de rotación, el cual, se refiere al movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original.
Es importante que recuerdes que la rotación conserva la medida de sus lados, la medida de sus ángulos, su tamaño y forma, aun cuando la figura cambie de posición.
El reto de hoy:
Busca en tu libro de texto de Matemáticas de tercer grado, problemas y ejercicios similares a los que aprendiste hoy, para que los resuelvas y practiques lo que aprendiste.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: