Propiedades de los polígonos regulares
Propiedades de los polígonos regulares
Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: desarrollar el razonamiento deductivo al examinar las propiedades de los polígonos regulares.
¿Qué vamos a aprender?
Continuarás con el estudio de las figuras geométricas. En esta sesión, conocerás cómo resolver problemas que implican obtener el número de diagonales que pueden trazarse desde un vértice, el número de diagonales en total y la suma de los ángulos interiores en polígonos regulares.
¿Qué hacemos?
Analiza la siguiente situación:
Problema 1
Alma tiene una casa en el interior de un terreno cuadrado, como se muestra en la siguiente figura:
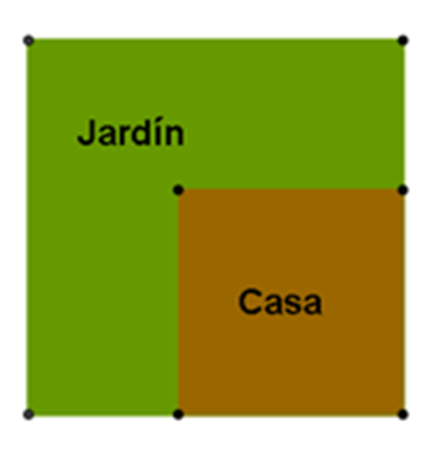
- ¿Qué polígonos puedes encontrar en la imagen?
- ¿Qué forma tienen la casa y el jardín?
Ella tiene dudas acerca del tipo de figuras que conforman su terreno. Su hijo pequeño le ha dicho que su jardín tiene forma rectangular y que su casa está construida sobre un terreno que tiene forma cuadrada, pero su hija, que está en la secundaria, no está de acuerdo, expresando que el jardín no tiene forma de un rectángulo, aunque tenga forma irregular.
Para salir de dudas, determina quién tiene la razón. Analiza:
¿Qué polígonos puedes encontrar en la imagen?
Para contestar esta pregunta, reflexiona un poco acerca de la forma que tienen los terrenos sobre la casa y el jardín:
¿Qué forma tienen la casa y el jardín?
Si se separa la casa y el jardín, puedes identificar dos polígonos diferentes.
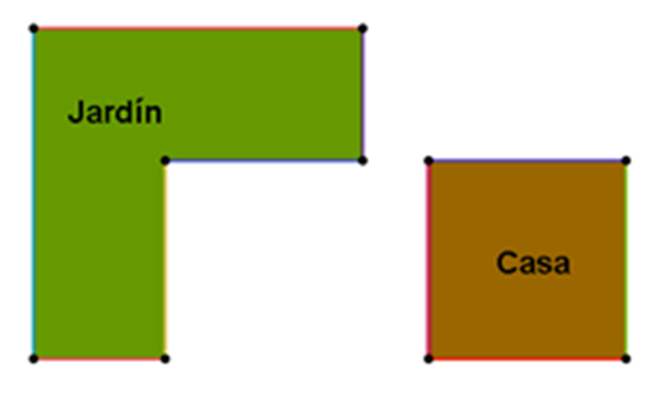
Analiza primero el terreno sobre el que está construida la casa.
¿Cuántos lados tiene el terreno sobre el que está construida la casa?
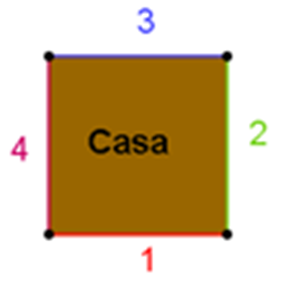
Al contar el número de lados, te puedes percatar de que son cuatro los lados del terreno sobre el que está construida la casa, entonces, es un cuadrilátero. Ahora, para determinar qué tipo de cuadrilátero es, necesitamos saber cuáles son las medidas de sus lados y de sus ángulos.
¿Cuáles son las medidas de sus lados entre sí?, ¿iguales o diferentes?
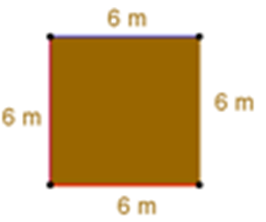
El primer lado mide 6 metros; el segundo, el tercero y el cuarto lado también miden 6 metros.
Como puedes observar, todos los lados tienen la misma medida, miden 6 metros, pero ¿esto quiere decir que se trata de un cuadrado? ¿Cómo puedes saberlo?
Para determinarlo, puedes recurrir a la medida de sus ángulos interiores.
Observa en el cuadrilátero ¿Cuál es la medida de sus ángulos interiores?
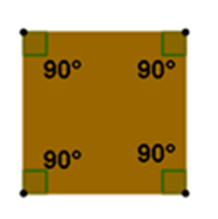
En el primer vértice, su ángulo mide 90 grados, el siguiente ángulo también es de 90 grados, en el tercer vértice su ángulo mide 90 grados y el cuarto ángulo es de 90 grados.
Entonces, como la medida de todos los ángulos interiores de este cuadrilátero es de 90°, puedes concluir que la casa de Alma está construida sobre un terreno cuadrado que representa un polígono regular.
De acuerdo con lo anterior, reflexiona en lo siguiente:
¿Cómo deben ser los ángulos interiores de un polígono para que éste sea regular?
¿Cómo deben ser los lados de un polígono para que éste sea regular?
Para poder dar respuesta a las preguntas anteriores sobre la casa de Alma, analiza lo siguiente y conoce más sobre los polígonos:
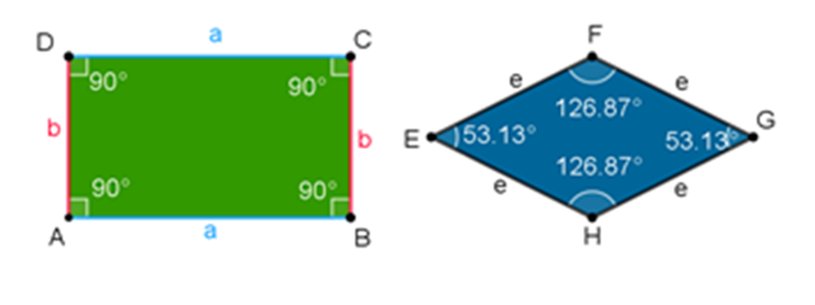
¿Por qué estos polígonos no son regulares?
El rectángulo no es regular porque, aunque sus ángulos interiores miden 90 grados, los lados no tienen la misma medida.
El rombo tampoco es regular porque, aunque la medida de sus lados es igual, la de sus ángulos interiores no lo es.
Regresando al problema inicial, ¿identifica qué tipo de polígono tiene el jardín de Alma?
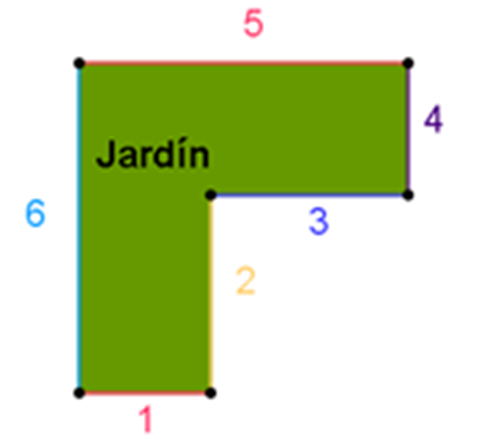
Por tener seis lados, el jardín es un hexágono, ¿y qué tipo de polígono es, regular o irregular?
Al analizar los lados, puedes observar sin necesidad de medirlos, que su longitud es diferente, por lo tanto, se trata de un polígono irregular.
Has analizado que, para que un polígono sea regular, es necesario que se cumplan a la vez las dos condiciones:
- Que la longitud de todos sus lados sea igual.
- Que la medida de todos los ángulos interiores sea igual.
Ahora analiza las diagonales que pueden trazarse desde un vértice y las diagonales totales que tienen los polígonos regulares.
Para esto, resuelve la siguiente situación.
Problema 2
En el parque hay tres diferentes áreas para juegos infantiles en forma de pentágonos regulares seccionados, como se muestra en la siguiente figura.
Identifica en cuál de ellos se utilizan las diagonales.
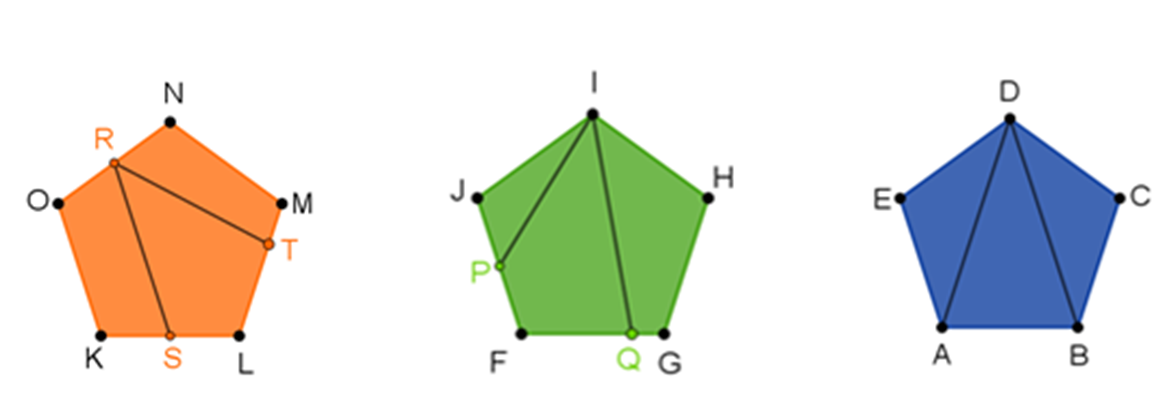
Después de haber leído el problema, analiza el primer polígono.
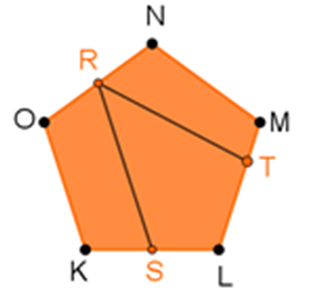
¿Cómo es que está seccionado este polígono?
Primero identifica los puntos que se encuentran marcados en el polígono.
- Los vértices del polígono son los puntos K, L, M, N y O.
- R es el punto medio del lado (NO).
- S es el punto medio del lado (KL).
- T es un punto que pertenece al lado (LM).
Este polígono está seccionado por dos segmentos de recta, el primero es el segmento “RS” y el segundo es el segmento “RT”.
El origen de la palabra diagonal hace alusión a los vértices de un polígono, por lo tanto, los segmentos RS y RT no pasan por los vértices, entonces no son sus diagonales.
Analiza el segundo polígono, ¿está seccionado por sus diagonales?
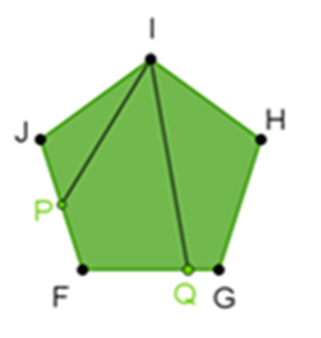
- Los vértices del polígono son los puntos F, G, H, I y J.
- P es el punto medio del segmento (JF).
- Q es un punto que pertenece al segmento (FG).
- Los segmentos con los que está seccionado el pentágono son “IP” e “IQ”.
Reflexiona sobre la siguiente pregunta:
¿Los segmentos que dividen el polígono pasan por dos vértices?
El segmento “IP” y el segmento “IQ” pasan por un solo vértice, esto quiere decir que esos segmentos no son sus diagonales.
Analiza el tercer pentágono y determina si está dividido por sus diagonales.
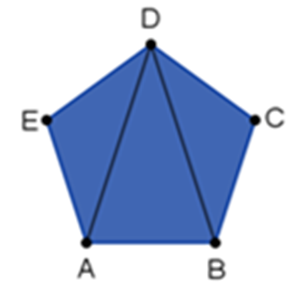
Los vértices del polígono son los puntos A, B, C, D y E.
¿Cuáles son los segmentos que dividen el pentágono?
Los segmentos que dividen al pentágono son (DA) y (DB).
¿Estos segmentos van de un vértice a otro vértice?
Estos segmentos pasan por dos vértices y dividen el polígono, entonces puedes concluir que los segmentos (DA) y (DB) son las dos diagonales del vértice D.
¿Todos los segmentos que van de vértice a vértice son diagonales?
Observa el pentágono, los segmentos “DE” y “DC” no son diagonales, ya que forman parte de los lados del pentágono. Entonces, las diagonales son segmentos de recta trazados de un vértice a otro vértice, no contiguos o no consecutivos.
A continuación, presta atención al siguiente problema.
Problema 3
¿Cuántas diagonales pasan por un vértice en cualquier polígono regular?
Analiza cuántas diagonales se pueden trazar desde un solo vértice en un cuadrado, un pentágono y un hexágono.

Los cuatro vértices del cuadrado son A, B, C y D, ahora considera el vértice A y traza todas sus diagonales.
¿Cuántas diagonales se pueden trazar?
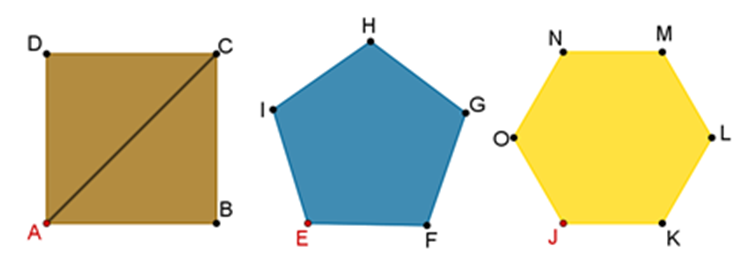
En el cuadrado, sólo se puede trazar una sola diagonal partiendo del vértice A, correspondiente al segmento (AC).
Ahora, traza las diagonales que sean posibles desde el vértice E en el pentágono.
¿Cuántas diagonales se pueden trazar desde el vértice E?
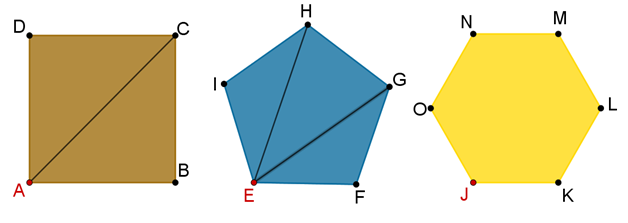
En el pentágono se pueden trazar dos diagonales, correspondientes a los segmentos (EH) y (EG).
¿Cuántas diagonales consideras que se pueden trazar en el hexágono desde el vértice “J”? y ¿cuáles son?
Traza las diagonales en el hexágono desde el vértice “J”.
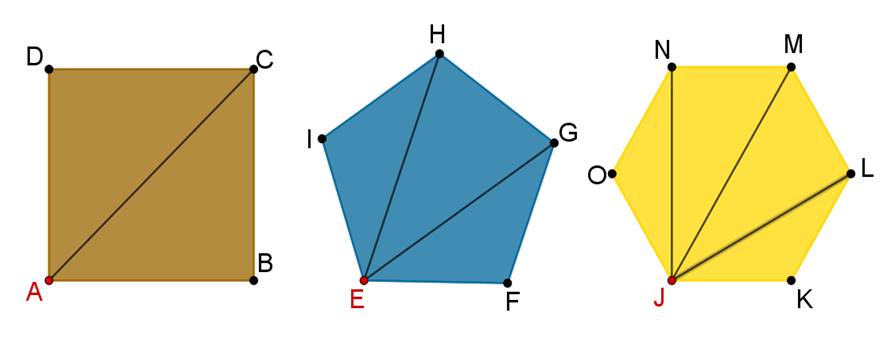
Las diagonales son 3, (JN), (JM) y (JL).
Da seguimiento a las preguntas anotándolas en tu cuaderno. Traza las figuras y usa colores para diferenciar las diagonales.
¿Cuántas diagonales se pueden trazar desde un vértice para cualquier polígono regular de “n” lados?
Para responder esta pregunta, elabora una tabla, ésta te ayudará a encontrar un patrón y te permitirá hallar el número de diagonales que se pueden trazar desde un solo vértice, aplicable a cualquier polígono regular.
En la primera columna anotarás el nombre del polígono regular; en la segunda, el número de vértices que tiene cada polígono, y en la tercera, el número de diagonales que se pueden trazar desde un vértice.
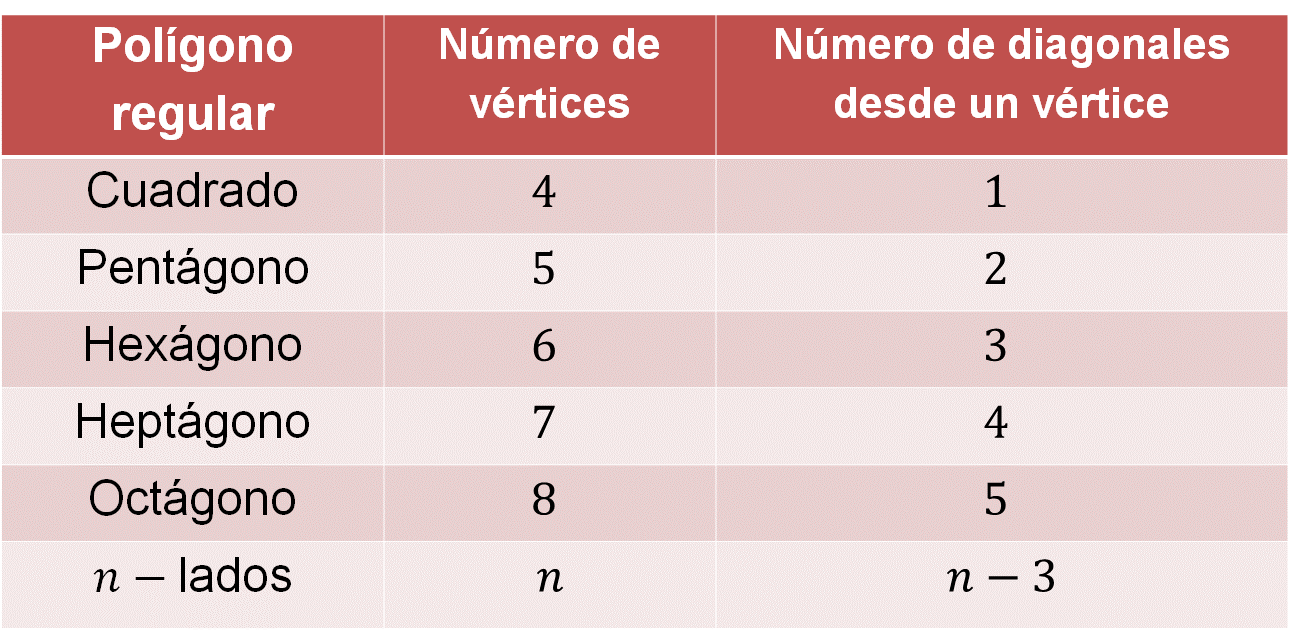
Al trazarse las diagonales desde un vértice y al no poderse trazar con los dos vértices contiguos, debes considerar tres vértices menos para encontrar el número de diagonales que se pueden trazar desde un solo vértice.
Por lo tanto, para cualquier polígono regular de “n” lados, tendrás:
n – 3 diagonales que pueden trazarse desde un vértice
Has aprendido a identificar los polígonos regulares, y a encontrar el número de diagonales que pueden trazarse desde un vértice en un polígono regular.
Ahora, examina todas las diagonales que se pueden trazar.
En tu cuaderno bosqueja un cuadrado, un pentágono y un hexágono, y traza todas las diagonales que te sean posibles en todos los vértices.
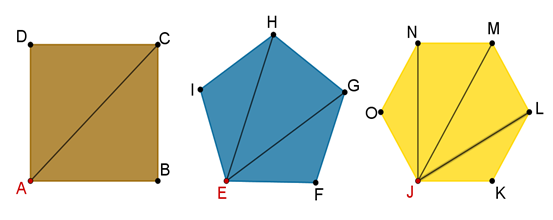
Ya que tengas todos tus trazos de las tres figuras, compáralos; seguramente tus trazos son parecidos a los que se presentarán a continuación:
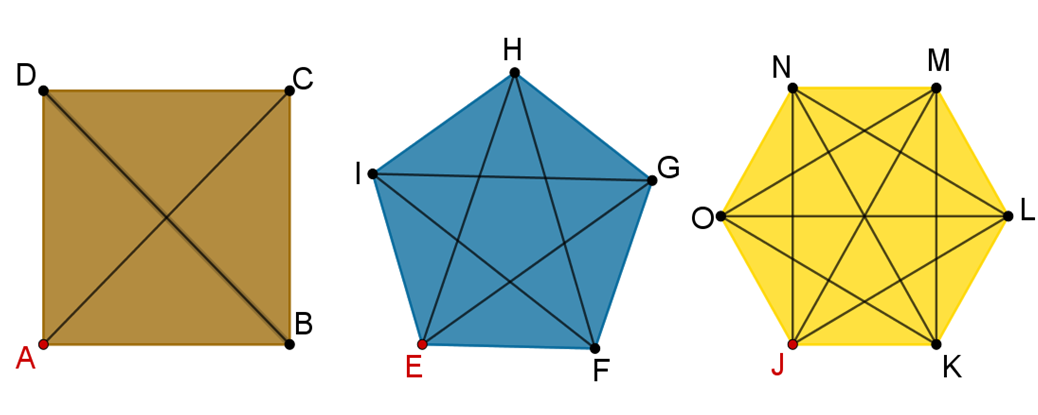
Te habrás dado cuenta de que, al trazar todas las diagonales de todos los vértices, las diagonales se repitieron. Por ejemplo, en el cuadrado, la diagonal que se trazaron desde “A” hasta “C” es la misma que se trazó de “C” hasta “A”, y esto mismo ocurre para todas las diagonales.
Ahora remarca de diferente color cada una de las diagonales para cada polígono sin repetirlas, para así poder contabilizar el número de diagonales totales. Observa el ejemplo:
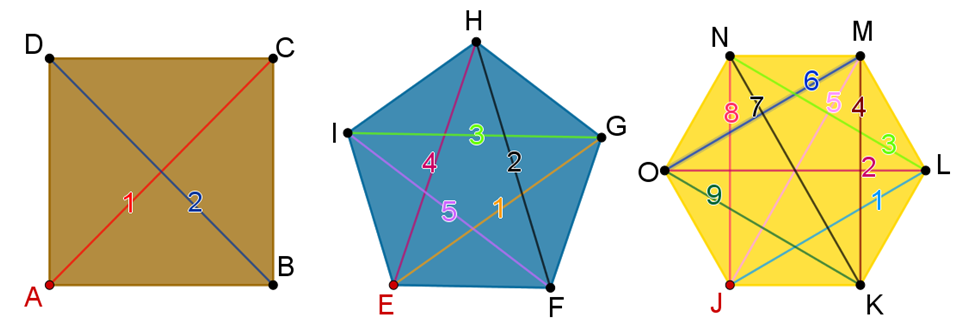
¿Cuántas diagonales tiene el cuadrado?
Para el cuadrado se tienen: dos diagonales totales.
Ahora cuenta cuántas diagonales totales tiene el pentágono:
Son cinco las diagonales totales del pentágono.
Finalmente, realiza lo mismo con el hexágono:
Son nueve las diagonales totales que tiene el hexágono.
Recapitulando, para el cuadrado se tienen dos diagonales totales, para el pentágono son cinco y para el hexágono son nueve.
¿Cómo puedes obtener el número de diagonales totales de cualquier polígono sin realizar los trazos y el conteo?
Analiza a detalle la información que has obtenido.
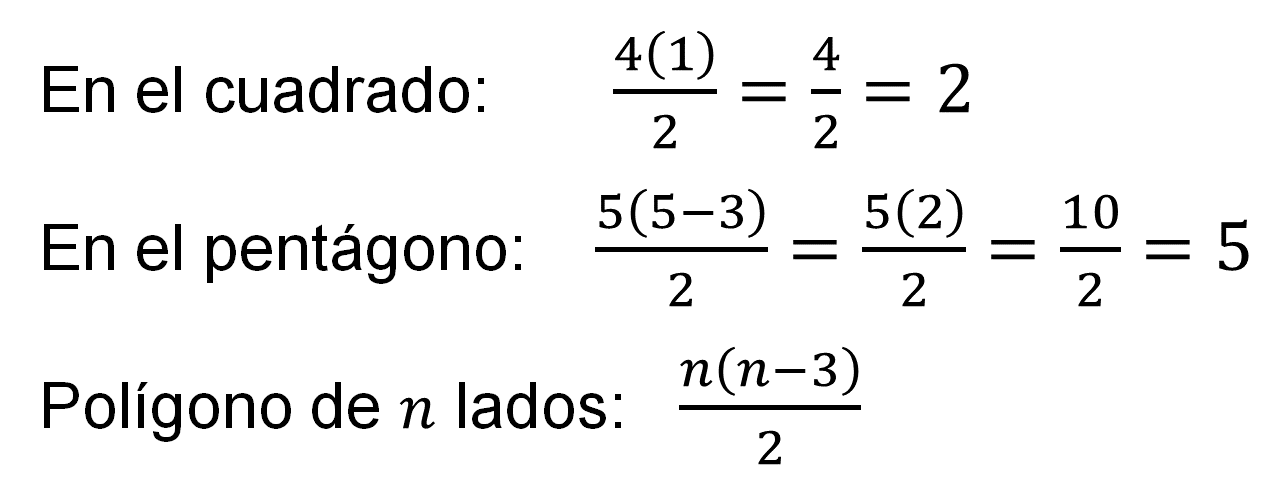
En el cuadrado, si se trazan las diagonales de todos los vértices, que son 4, a cada vértice se le podría trazar (1) diagonal, de forma que se podrían considerar 4 diagonales totales, sin embargo, se repiten el doble de diagonales; para evitar repetirlas, se dividen entre dos, por ello aparecen sólo dos.
En el pentágono, si se trazan todas las diagonales desde cada vértice, se deben multiplicar el número de vértices (5), por el número de diagonales que se pueden trazar desde cada vértice (5 – 3), es decir, 5(2) que son 10. Pero aquí se están considerando el doble de las diagonales porque éstas se duplican, y para no duplicarlas, tienes que dividir entre dos el producto, esto es: 10/2, igual a 5.
Generalizando, para un polígono regular de “n” lados. Si para un vértice se pueden trazar “n – 3” diagonales, para “n” vértices serán “n (n – 3)” diagonales, pero no se ha considerado que las diagonales se duplican y para no duplicarlas tienes que dividir entre dos este producto, quedando la expresión:
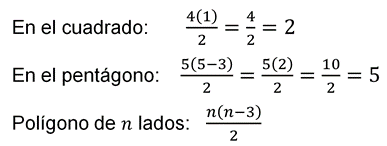
Para corroborar que la generalización es correcta, puedes realizar una sustitución numérica y verificar que se cumple para los polígonos que has analizado.
A continuación, realiza la comprobación.
Para un cuadrado que tiene cuatro vértices, “n” es igual a cuatro, y al sustituirlo en la generalización se tiene que el número total de diagonales es igual a “n”, por lo tanto:

Realiza la siguiente actividad:
Corrobora en tu cuaderno los polígonos regulares de 5 y 6 lados al sustituir “n” igual a cinco y “n” igual a seis, respectivamente.
Como ésta es una generalización, ahora puedes calcular el número de diagonales totales que tiene un icoságono regular, que es un polígono de veinte lados. Realízalo.
Hasta este momento has aprendido a identificar los polígonos regulares, a encontrar el número de diagonales que pueden trazarse desde uno de sus vértices y a encontrar el número de sus diagonales totales.
Ahora, explorarás diferentes polígonos para obtener la suma de los ángulos interiores en un polígono regular.
Analiza los siguientes polígonos regulares:
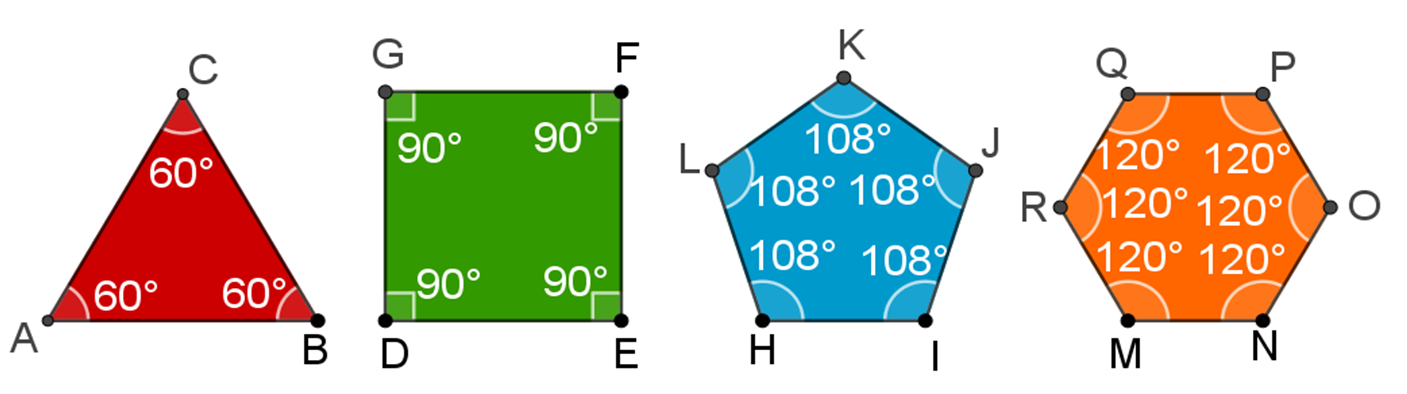
Recuerda que, para que sean polígonos regulares, la longitud de todos sus lados es igual y, además, todos sus ángulos interiores también son iguales.
Comienza con el triángulo equilátero:
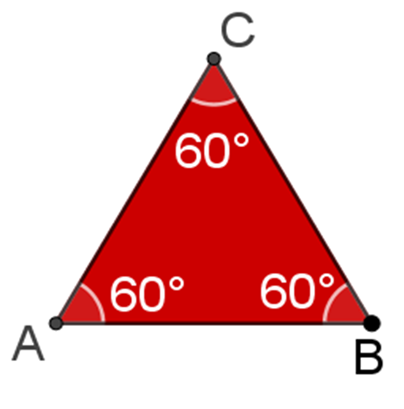
Este triángulo tiene tres lados y tres vértices, y además mide 60 grados en cada uno de sus ángulos interiores.
¿Cómo puedes encontrar la suma de sus ángulos interiores?
Se puede obtener de dos formas: sumando 60 grados 3 veces o multiplicando tres por sesenta grados, es decir, 180 grados.
60° + 60° + 60° = 3 (60°) = 180°
Continúa con el cuadrado:
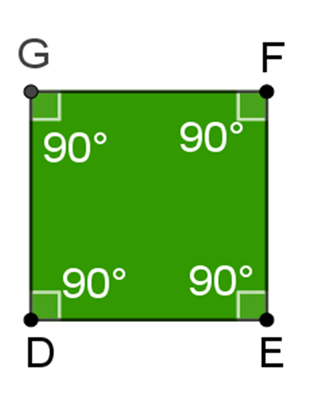
Este polígono tiene cuatro lados y cada uno de sus ángulos interiores mide 90 grados, entonces la suma de sus ángulos interiores se obtiene multiplicando 4 por 90 grados, igual a 360 grados.
4 (90°) = 360°
Ahora con el pentágono:
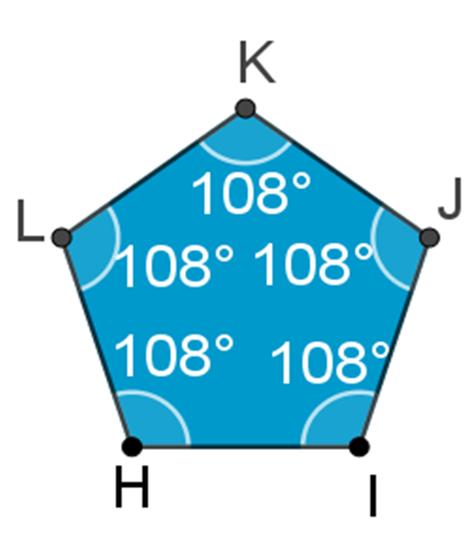
Como tiene cinco ángulos interiores y cada ángulo interior tiene una amplitud de 108 grados, entonces la suma de los ángulos interiores corresponde al producto de 5 por 108 grados, es decir, 540 grados.
5 (180°) = 540°
Finalmente, con el hexágono.
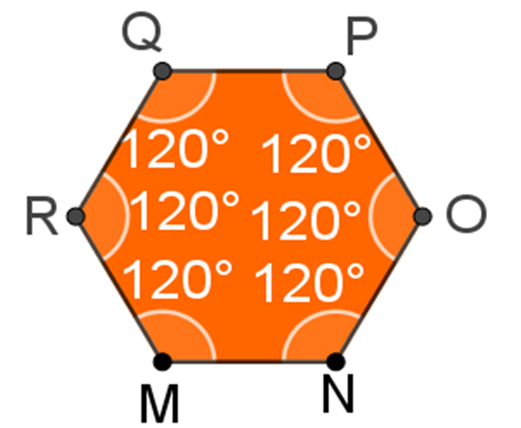
El hexágono, es un polígono de seis lados con seis vértices, y cada ángulo interior mide 120 grados, entonces la suma de sus ángulos interiores es 6 por 120 grados, o la multiplicación de 6 por 120 grados, es igual a 720 grados.
6 (120°) = 720°
Recapitulando:
La suma de los ángulos interiores de:
- un triángulo equilátero es: 3(60°) = 180°
- un cuadrado es: 4(90°) = 360°
- un pentágono regular es: 5(108°) = 540°
- un hexágono regular es: 6(120°) = 720°
Generalizando, se tiene que la suma de los ángulos interiores de un polígono regular es el producto del número de lados o vértices por la amplitud de uno de sus ángulos interiores.
A continuación, analiza los polígonos y traza en uno solo de sus vértices todas las diagonales posibles.
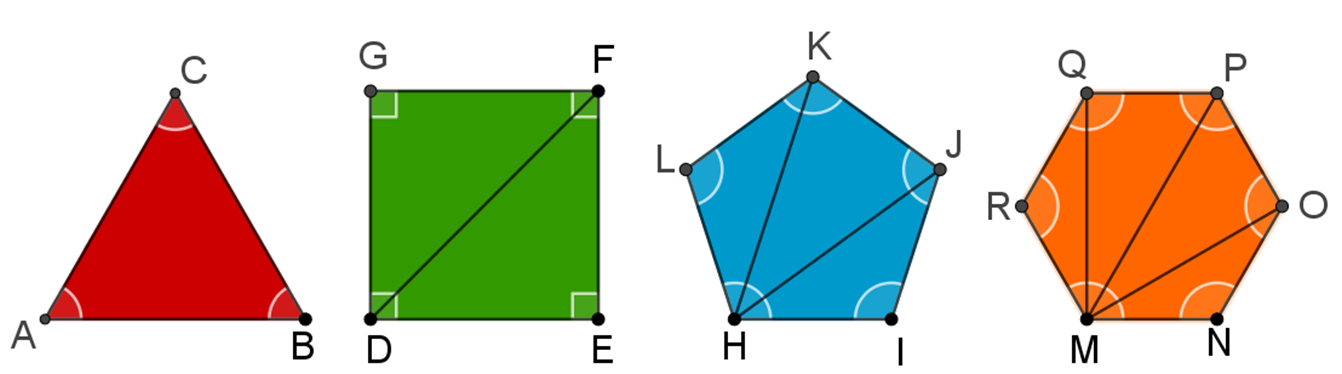
En el triángulo no se tienen diagonales, por lo tanto, el número de diagonales es cero, en el cuadrado el número de diagonales es 1, en el pentágono es 2, en el hexágono hay 3 y así sucesivamente.
Examina cuántos triángulos se pueden formar en un cuadrado al seccionarlo por medio de su diagonal.
¿Cuántos triángulos se forman en un cuadrado?
Dos triángulos.
Si se sabe que la suma de los ángulos interiores de un triángulo es de 180 grados, en un cuadrado que está conformado por dos triángulos, ¿cuánto medirá la suma de sus ángulos interiores?
Si en un triángulo la suma de los ángulos interiores es de 180 grados, la de un cuadrado conformado por dos triángulos será el doble de 180 grados, esto es, dos por 180 grados, es decir, 360 grados.
Analiza el pentágono.
Al trazar las diagonales que pasan por uno solo de sus vértices, ¿cuántos triángulos se forman?
Se forman tres triángulos
Por lo tanto, ¿cómo puedes obtener la suma de los ángulos interiores de un pentágono?
Como el número de triángulos que se forman al trazar las diagonales desde un vértice son tres, entonces la suma de los ángulos interiores del pentágono regular se obtiene al multiplicar 3 por 180 grados, que es igual a 540 grados.
Para el hexágono.
La suma de los ángulos interiores es 4 por 180 grados, que es igual a 720 grados.
Generalizando, se tiene que la suma de los ángulos interiores de un polígono regular se obtiene al multiplicar el número de triángulos que se forman al trazar desde un solo vértice todas sus diagonales por 180 grados.
¿Cómo puedes relacionar el número de triángulos que se pueden formar con el número de lados o vértices?
Organiza tu información en la siguiente tabla.
En la primera columna anotarás el polígono; en la segunda, el número de lados; en la tercera, el número de triángulos, y en la cuarta columna, la suma de los ángulos interiores del polígono regular.
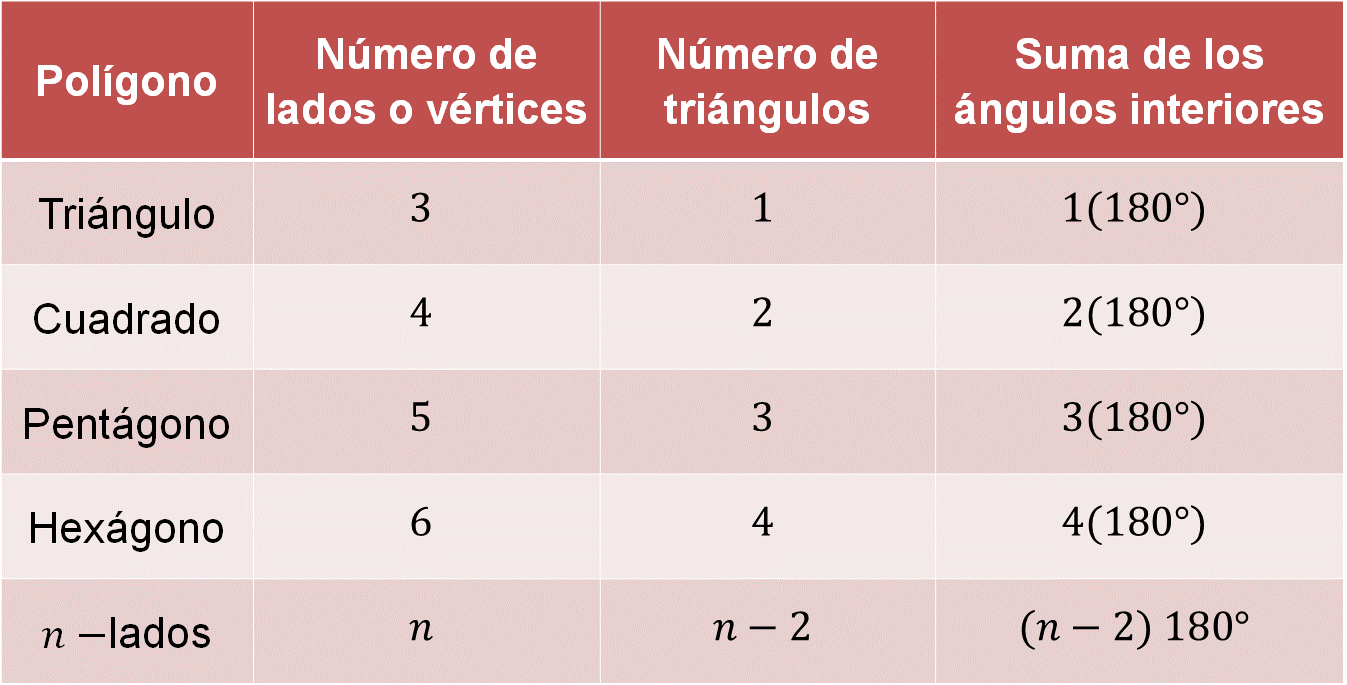
Para un triángulo con 3 lados, el número de triángulos es 1 y la suma de los ángulos interiores es 1 por 180 grados.
En un cuadrado el número de lados es 4, el número de triángulos es 2 y la suma de los ángulos interiores es 2 por 180 grados, y así sucesivamente.
Observamos que, para un polígono de “n” lados, el número de triángulos que se pueden formar es el número de lados menos dos, y la suma de los ángulos interiores de un polígono es el número de triángulos que se pueden trazar desde un vértice que es “n – 2” por 180 grados.
El reto de hoy:
Traza un decágono regular y las diagonales de todos sus vértices en tu cuaderno. Corrobora que el número de diagonales totales coincidan con el obtenido por medio de la generalización.
Finalmente, utilizando la generalización, responde cuánto debe medir el ángulo interior para el polígono y confírmalo midiendo uno de los ángulos interiores del polígono que trazaste.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/