Problemas que se resuelven mediante ecuaciones de segundo grado
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: modelado de ecuaciones de segundo grado.
¿Qué vamos a aprender?
Trabajarás problemas que se resuelven mediante ecuaciones de segundo grado, con la intención de identificar el modelo de dichas ecuaciones, a través del planteamiento de una situación real.
¿Recuerdas el problema de los dos reinos y el dragón? Recuerda el cuento: El mundo de las ecuaciones

Hasta hoy has trabajado con una forma para hallar el valor de la incógnita.
¿Qué hacemos?
Observarás la siguiente cápsula que te ayudará a determinar la forma de la ecuación.
- Identificar tipos de ecuaciones cuadráticas
https://pruebat.org/sabermas/miclase/inicia/9610/c5c15cef4825929e62345928b33fe76d/158743/2-156
Continua con el trabajo para solucionar la ecuación del dragón Operagron.
Es importante que ahora que conoces la solución de problemas por medio de ecuaciones cuadráticas, establezcas que son una herramienta planteada al traducir el enunciado del problema en una ecuación de estas.




Observa el siguiente video para retomar todo lo que has aprendido. - Resolver ecuaciones cuadráticas puras
https://aprende.org/pages.php?r=portada_course_view&tagID=1677&load=3723
Las ecuaciones cuadráticas o de segundo grado se resuelven agrupando los términos semejantes y despejando la incógnita.
Resuelve un problema de Física de caída libre. Observa qué ocurre en un clavado. - Clavado de Paola Espinosa. acervo televisión educativa:
Ciencias y Tecnología. Física.
Segundo grado. Bloque 1.
https://www.youtube.com/watch?v=BRhoWtjzoYE
¿Pudiste identificar la expresión obtenida como una ecuación de segundo grado?
Aquí el término cuadrático o elevado al cuadrado fue el tiempo. Reflexiona cómo cambia la velocidad a medida que varía, y cómo se acelera la caída debido a la gravedad.
¿Y qué pasó con la distancia?
Si Paola hubiera seguido cayendo y llegado a los siguientes 100 metros, hubiera quedado algo así:
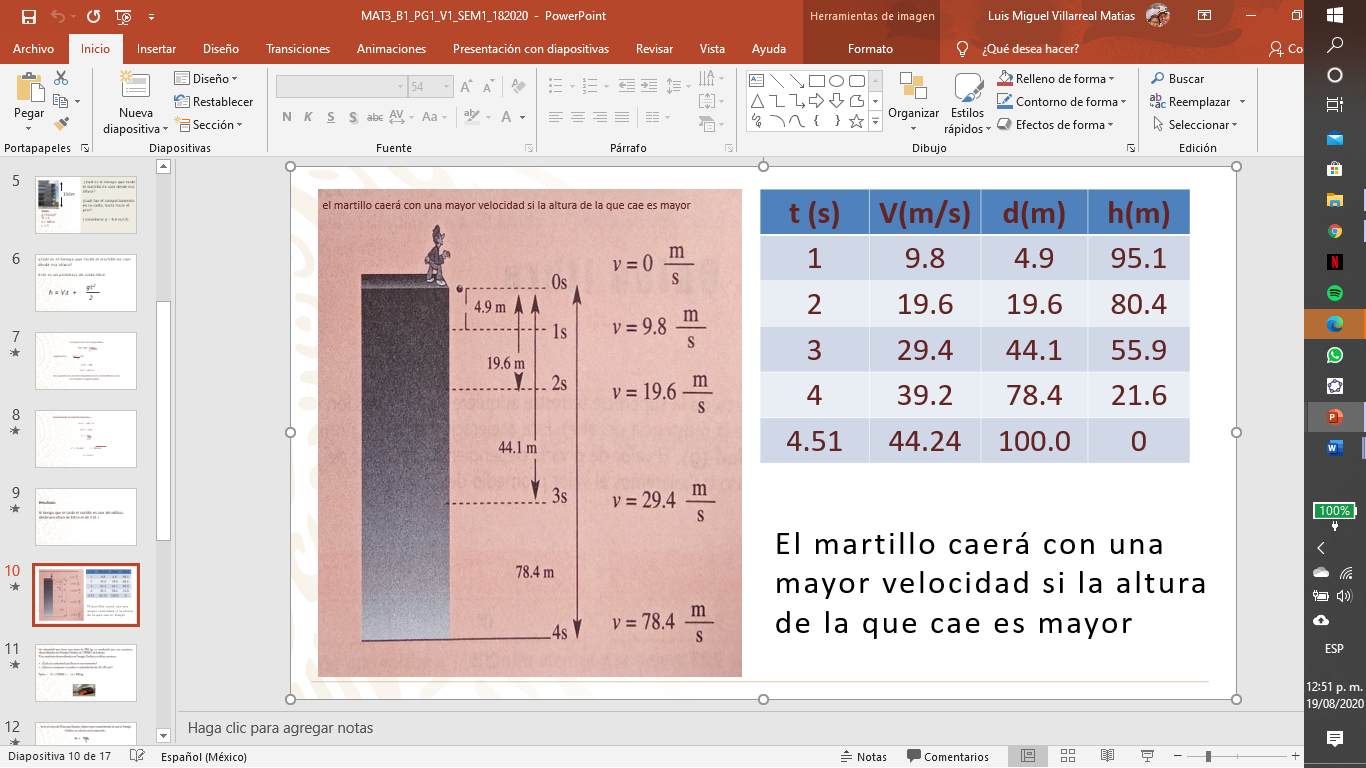
Estas son las características de un comportamiento cuadrático.
El reto de hoy:
A lo largo de estas clases, has visto desde cómo puedes plantear un problema con una ecuación cuadrática simple y las diferentes formas en que esta se resuelve, hasta las respuestas a las preguntas que surgen del mismo.

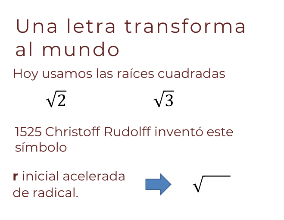
Usas las raíces cuadradas √2, √3, colocando al pobre número debajo de una especie de uve con raya, como si de un paraguas numérico se tratara. Esto es así desde 1525 cuando Christoff Rudolff inventó este símbolo √ que no era otra cosa que una escritura acelerada de la letra r inicial de radical.
Puedes consultar tu libro de texto de Matemáticas de Tercer Grado, buscar el tema de ecuaciones cuadráticas y practicar con los ejemplos propuestos en él.
¡Buen trabajo!
Gracias por tu esfuerzo.