Pensamiento proporcional
Pensamiento proporcional
Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.
Énfasis: dar sentido y significado a las propiedades del razonamiento proporcional.
¿Qué vamos a aprender?
Estudiarás y comprenderás cómo se resuelven problemas de proporcionalidad directa. Asimismo, aprenderás a dar sentido y significado a situaciones relacionadas con el razonamiento proporcional.
¿Qué hacemos?
Para iniciar, resuelve las siguientes situaciones cotidianas.
Situación, lápiz
Si un lápiz cuesta 6 pesos, ¿cuánto costarán dos, tres, cuatro o cinco lápices?
Si un lápiz cuesta en promedio 6 pesos, entonces dos lápices costarán el doble de lo que cuesta un lápiz, esto es, 2 por 6, es igual a 12 pesos. Y tres lápices costarán el triple de lo cuesta un lápiz, es decir, 3 por 6, 18 pesos. Cuatro lápices costarán, 4 por 6 igual a 24 pesos. Y 5 lápices costarán 5 por 6 igual a 30 pesos.
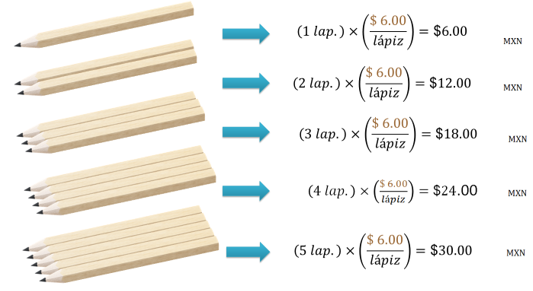
¿Contestaste correctamente? Si no es así, revisa la fuente del error y corrige.
Continúa con la siguiente situación.
Situación, tortillas
Si un kilogramo de tortillas cuesta en promedio 13 pesos, ¿cuánto cuestan 3 kilogramos?, ¿medio kilogramo? y ¿3 kilogramos y medio?
Si un kilogramo de tortillas cuesta 13 pesos, entonces tres kilogramos cuestan el triple de lo que cuesta 1 kilogramo, esto es, 3 por 13, igual a 39.
De la misma forma, como 1 kilogramo cuesta 13 pesos, medio kilogramo costará la mitad, es decir, 6 pesos con cincuenta centavos.
Si tres kilogramos cuestan 39 pesos y medio kilogramo cuesta 6 pesos con cincuenta centavos, entonces 3 kilogramos y medio costarán 39 más 6 cincuenta, igual a 45 pesos con 50 centavos.
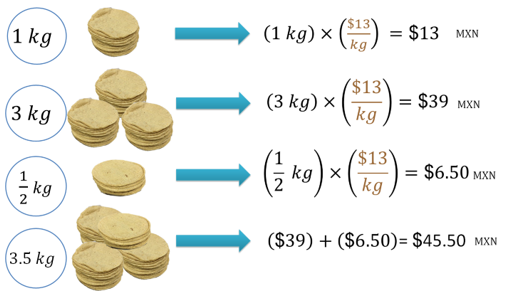
¿Ya comparaste tus resultados?
¿Lo resolviste correctamente?
Si no fue así, analiza el origen del error y corrígelo. Recuerda que esta es una oportunidad para aprender a resolver este tipo de problemas.
Ahora, analiza a detalle el siguiente problema relacionado con la producción de computadoras y sus accesorios.
Situación-problema, computadoras y accesorios
Con 10 metros de cable se fabrican los conectores a corriente para 4 computadoras portátiles. De acuerdo con la información anterior, contesta las siguientes preguntas.
- ¿Cuántas computadoras se pueden ensamblar si se cuenta con 20 metros de cable conector?
- ¿Cuántos metros de cable se requieren para fabricar los conectores de 12 computadoras?
- ¿Cuál es la razón unitaria?
- ¿Cómo puedes determinar el tipo de proporcionalidad que se requiere para resolver el problema?
Después de anotar las preguntas y de analizarlas, ¿ya sabes cómo resolver el problema?
Analiza lo que se plantea.
La información presentada en el problema la puedes organizar en una tabla. En la primera columna anota el número de computadoras y en la segunda columna anota la longitud de cable requerido en metros para determinado número de computadoras. De acuerdo con la información que se proporciona en el problema, en la primera columna se anotará 4, que corresponde al número de computadoras y en la segunda columna anotarás 10, que son los metros de cable que le corresponden a esas 4 computadoras.

Resuelve la primera pregunta:
¿Cuántas computadoras se pueden ensamblar si se cuenta con 20 metros de cable conector?
Anota la información que tienes en el siguiente renglón de la tabla.
¿En qué columna se anotan los 20 metros de cable?
Los anotarás en la segunda columna, porque en ella se anota la longitud del cable, puesto que su encabezado lo está indicando.

Analiza los datos en la tabla. Se sabe que para que se ensamblen 4 computadoras se requieren 10 metros de cable, entonces, ¿cuántas computadoras se ensamblan si se cuenta con 20 metros de cable?
Antes de dar solución a la pregunta, debes reflexionar acerca de si el número de computadoras debe ser mayor o menor que 4.
El número de computadoras que se pueden ensamblar con 20 metros de cable es mayor que 4.
Por lo tanto, puedes darte cuenta de que como la longitud 20 es el doble de 10, entonces el número de computadoras que se pueden ensamblar con 20 metros de cable debe ser el doble de 4, que es 8.

Esto quiere decir que al doble de la longitud del cable le corresponde el doble del número de computadoras que se pueden ensamblar y empaquetar.
Puedes concluir entonces que, a mayor longitud del cable, mayor será el número de computadoras que se pueden ensamblar y empaquetar.
Continúa con el siguiente cuestionamiento:
¿Cuántos metros de cable se requieren para fabricar los conectores de 12 computadoras?

Al preguntarle a Georgina y a Manuel, dos estudiantes de secundaria, cómo resuelven este problema, muestran dos estrategias diferentes de solución.
Georgina dice que, como para obtener 12 se multiplica 4 por 3, entonces para obtener la longitud del cable requerido se tendrá que multiplicar 10 por 3.
Por su parte, Manuel dice que para obtener 12 suma 4 más 8, por lo tanto, para obtener la longitud del cable suma 10 más 20.
Verifica quién está en lo correcto, si Georgina o Manuel.
Interpreta lo que Georgina dice:
Ya que para 4 computadoras se requieren 10 metros de cable y como el triple de 4 es doce, entonces la longitud que le corresponde a esas doce computadoras será el triple de 10 metros, que son 30 metros.
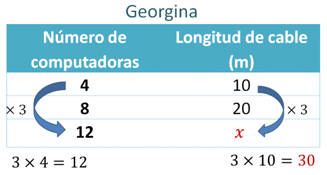
De acuerdo con lo que desarrolló Georgina, se puede inferir que, para el triple del número de computadoras, le corresponde el triple de la longitud del cable que para 4 computadoras. Por lo tanto, ella está en lo correcto.
Ahora, interpreta lo que dice Manuel.
Como para 4 computadoras se requieren 10 metros de cable y para 8 computadoras se requieren 20, entonces para 12 computadoras (que es la suma de 4 más 8) se requerirán 30 metros, que es la suma de los 10 metros correspondientes a las 4 computadoras, más los 20 metros correspondientes a las 8 computadoras.
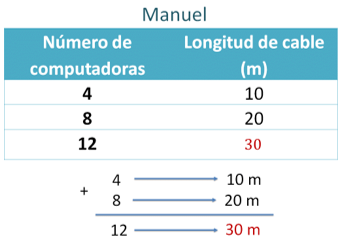
Puedes darte cuenta de que ambos obtuvieron que se requieren 30 metros de cable para ensamblar 12 computadoras, utilizando estrategias diferentes, y tanto Manuel como Georgina están en lo correcto.
Ahora obtén la razón unitaria, es decir, cuántos metros de cable se requieren para la producción de una sola computadora.
Si utilizas el razonamiento de Georgina, se puede decir que, como la cuarta parte de 4 computadoras es 1, entonces, la cuarta parte de su correspondiente, 10 metros de cable es 2.5 metros.
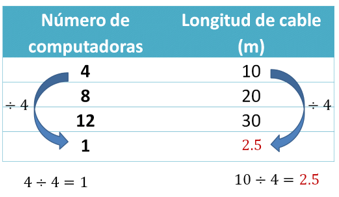
Ahora ya sabes que para una computadora se requieren 2.5 metros de cable y con esta información puedes determinar la razón unitaria; esto quiere decir que se requieren de 2.5 metros por cada computadora que se fabrique.
Para contestar la siguiente pregunta, es necesario que reflexiones acerca del tipo de problema que has resuelto.
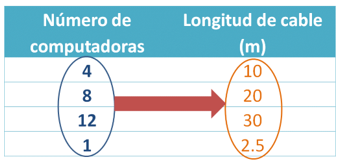
Con la información anterior puedes saber que, a mayor número de computadoras, mayor es la longitud del cable que se requiere y, como consecuencia, a menor número de computadoras, es menor la longitud del cable que se requiere.
¿Ya sabes qué tipo de problema es éste?
Para ello, analiza cómo está relacionado el número de computadoras con la longitud del cable.
¿Cómo puedes obtener la longitud del cable a partir del número de computadoras?
Al multiplicar 4, que es el número de computadoras, por 2.5, que es la razón unitaria, se obtiene 10, que es la longitud de cable en metros que se requiere para su fabricación.
Esto implica que, al relacionar la longitud del cable de 10 m entre el número de computadoras, 4, se obtiene la razón 2.5 metros por computadora.
Pero ¿sucede lo mismo con todas las parejas de la tabla?
Observa lo siguiente:

Al relacionar 20 metros con 8 computadoras, se obtiene una razón de 2.5 metros por computadora.
Y al relacionar 30 metros con 12 computadoras, también se obtiene una razón de 2.5 metros por computadora.
Por lo tanto, es un problema de proporcionalidad porque las variables están relacionadas por medio de una razón. Y como esa razón es constante, se le llama constante de proporcionalidad “k”. Entonces, la constante de proporcionalidad en este caso es de 2.5 metros de cable por computadora.
Con lo anterior, ya puedes contestar la última pregunta del problema.
¿Cómo puedes determinar el tipo de proporcionalidad que se requiere para resolver el problema?
Las variables (que son el número de computadoras y la longitud del cable que se requiere para su fabricación) están relacionadas directamente por medio de la constante de proporcionalidad. Esto quiere decir que cuando aumenta el número de computadoras para ensamblar, también aumenta la longitud del cable requerida para su fabricación. De la misma forma, cuando disminuye el número de computadoras, también disminuye de manera proporcional la longitud del cable. Por estar relacionadas de manera directa, se dice que la proporcionalidad entre estas variables es directa.
Has finalizado la resolución de este problema.
Resuelve un nuevo problema para que pongas en práctica lo aprendido.
Situación-problema, auto
Un auto subcompacto recorre 101 km con 5 litros de gasolina.
¿Cuántos litros se requieren para recorrer 202 km?
¿Cuántos kilómetros se pueden recorrer con 15 litros?
¿Cuál es la constante de proporcionalidad?
¿Qué significa esa constante?
Para resolver lo que se plantea, organiza la información en una tabla como lo hiciste en el problema anterior.
¿Ya sabes cuántas columnas tendrá la tabla?, y ¿cuál es el encabezado de ésta?
Analiza las variables que intervienen en el problema. Se enuncian dos variables: los litros de gasolina que utiliza el auto y la distancia que se puede recorrer. Entonces la tabla consta de dos columnas con su correspondiente encabezado, el primero de ellos se refiere a los litros de gasolina y el segundo a la distancia en kilómetros.
En el primer renglón de la tabla anota los datos del problema. Con 5 litros de gasolina se recorre una distancia de 101 kilómetros.

Entonces, se puede decir que, a 5 litros, le corresponden 101 kilómetros.
Para contestar la primera pregunta referente a cuántos litros se requieren para recorrer 202 kilómetros, puedes reflexionar con el siguiente cuestionamiento:
Si a 5 litros le corresponden 101 kilómetros, ¿cuántos litros les corresponderán a 202 kilómetros?

Seguramente ya identificaste que como 202 es el doble de 101, los litros que se requieren para recorrer esa distancia son el doble de 5, es decir, 10.

Ahora piensa: ¿cuántos kilómetros se pueden recorrer con 15 litros?

Al analizar la tabla, se identifica que se puede utilizar la estrategia de Georgina.
Ella decía que al triple le toca el triple. Es decir, como el triple de 5 es 15, entonces el triple de 101 es 303.
También se puede usar la estrategia de Manuel, esto es, como 15 es 5 más 10, entonces la distancia que le corresponde a 15 será 101 más 202, que son 303 kilómetros.
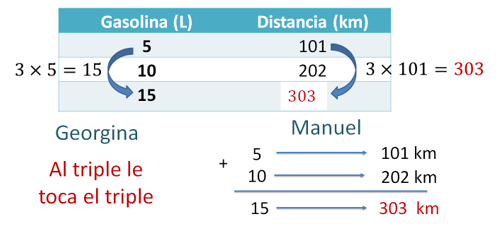
Ahora obtén la constante de proporcionalidad.
¿Ya sabes cómo calcularla?
Recuerda que la constante de proporcionalidad se obtiene al relacionar las variables que se están analizando, en este caso, se relaciona la distancia en kilómetros con los litros de gasolina requeridos para recorrerla.
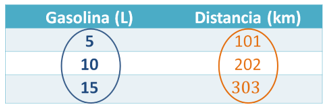
Entonces, se puede obtener de cualquiera de las tres parejas con las que se cuenta. Hazlo con los datos originales enunciados en el problema. La constante de proporcionalidad “k” es igual a 101 kilómetros entre 5 litros, esto es igual a 20.2 kilómetros por litro.
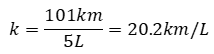
Y si divides 202 kilómetros entre 10 litros, también obtienes la misma razón; por eso se le llama constante: porque su valor no varía.
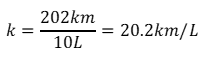
Ya has calculado el valor de la constante de proporcionalidad, pero ¿cuál es el significado que tiene este número?
Es el rendimiento, esto quiere decir que el auto subcompacto por cada litro de gasolina puede recorrer o rendir hasta 20.2 kilómetros.
¿Para qué sirve esta información?
Respondiendo a esta pregunta, debes saber que cada auto tiene un rendimiento especificado por el fabricante y esta es una de las variables que puede ayudar a tomar decisiones cuando se realiza la compra del auto.
Para tener una idea de lo importante que es realizar una buena elección con base en la información que proporciona un fabricante de autos, analiza detenidamente la siguiente información.
Algunos autos compactos tienen un rendimiento de 15 kilómetros por litro. Si se compara el rendimiento de algunos autos subcompactos y de autos compactos, se tiene que el auto subcompacto del problema tiene un rendimiento del 20.2 kilómetros por litro.

¿Cuál auto conviene si lo que se quiere es economizar gasolina?
Al comparar los rendimientos de ambos autos, puedes obtener cuántos litros de gasolina se requieren para recorrer la misma distancia.
Se puede suponer que recorrerán 10 kilómetros.
¿Cuántos litros de gasolina requieren ambos autos para recorrer esa distancia?
Comienza con el auto subcompacto.
En la tabla que relaciona los litros de gasolina con la distancia que se puede recorrer, se identifica que la distancia recorrida “y” en kilómetros es igual a los litros de gasolina “x”, por su rendimiento, 20.2.
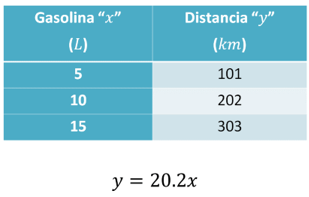
Esto puedes comprobarlo fácilmente con los datos de la tabla.
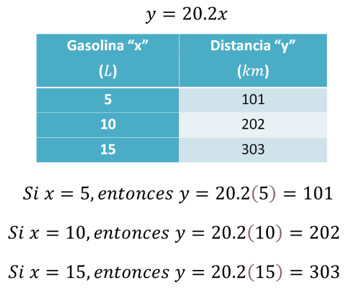
Entonces, ¿cuánto debe valer “x” para que “y” sea de 10 kilómetros?
Al sustituir “y” igual a 10, en la relación proporcional, se tiene que 10 es igual a 20.2 “x”.
Para encontrar un número “x” tal que al multiplicarlo por (20.2) obtengas como resultado 10, se resuelve con el inverso de la multiplicación, que es la división, es decir, “x” es igual a 10 entre 20.2, que aproximadamente es 0.495 L, un poco menos de medio litro.

Ahora obtén cuántos litros se requieren para que un auto compacto recorra 10 kilómetros con un rendimiento de 15 kilómetros por litro.
La relación para este tipo de autos es “y”, en kilómetros es igual a 15, que es el rendimiento, por los litros de gasolina “x”.
Al sustituir “y” igual a 10, en la relación proporcional, se tiene que 10 es igual a 15 “x”.
Para obtener el valor de “x” divide 10 entre 15, que aproximadamente es igual a 0.666 litros.
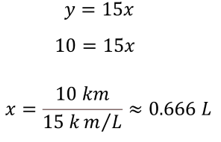
Finamente, compara los litros que se requieren para recorrer la misma distancia en ambos autos.

El auto subcompacto requiere 0.495 litros de gasolina aproximadamente, mientras que el auto compacto requiere 0.666 litros de gasolina, aproximadamente.
¿Cuál de los dos conviene comprar si lo que quiere es economizar gasolina?
Obviamente es el auto subcompacto, ya que requiere menor cantidad de gasolina, y si se gasta menos gasolina, se gasta menos dinero que se puede ahorrar.
Con lo anterior, puedes darte cuenta de que conviene comprar un auto que tiene mayor rendimiento que otro con menor rendimiento, ya que el gasto que se requiere por la compra de gasolina será menor. Por ello es que el rendimiento es una especificación muy importante que proporcionan los fabricantes de autos.
Para finalizar, recapitula lo que has estudiado.
Una relación es de proporcionalidad directa cuando se relacionan dos variables por medio de una razón llamada constante de proporcionalidad, siempre que su forma algebraica sea “y” igual a “k” por “x”, en donde “x” y “y” son las variables, y “k” es la constante de proporcionalidad.
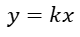
Con esto has finalizado la sesión, dedicada a dar sentido y significado a las propiedades del razonamiento proporcional.
Recuerda que este es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.
El reto de hoy:
Resuelve la siguiente situación-problema.
Situación-problema, construcción
Tres albañiles tardan en construir 6 metros cuadrados de pared en un día, ¿cuánto tiempo se tardarán en construir una pared de 15 metros cuadrados?
Primero identifica si la relación entre las variables presentadas en el problema es de proporcionalidad directa o no, y argumenta por qué. Antes de realizar los cálculos, realiza una estimación y posteriormente procede a realizar el cálculo. Finalmente, verifica si tu resultado es coherente o no, y compáralo con tu estimación.
Finalmente, piensa en otras situaciones cotidianas en las que se utilice el razonamiento proporcional. Escríbelas en tu cuaderno, analízalas y, de ser posible, identifica la expresión algebraica que las modela.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas