Pendiente y tangente
Pendiente y tangente
Aprendizaje esperado: resuelve problemas que implican el uso de las razones trigonométricas seno, coseno y tangente.
Énfasis: analizar la relación entre la pendiente y la recta tangente en problemas geométricos.
¿Qué vamos a aprender?
Analizarás la relación entre la pendiente y la recta tangente en algunos problemas geométricos.
Los materiales que utilizarás es tu cuaderno, lápiz, goma, y de contar con ella, una calculadora científica.
Toma nota en tu cuaderno de las ideas o inquietudes que surjan durante la sesión.
Conocerás la relación que tienen entre si la tangente y la pendiente de una recta,
¿Qué hacemos?
Inicia con el concepto de ¿qué es una pendiente de una recta?
Y para ello, Moisés, que es estudiante de secundaria te lo dirá:
- Video 1 Moisés
https://youtu.be/1Hfas20aiU8
(del min. 1.25 al 1.43)
Esa es una definición técnica, retoma entonces la definición de Moisés con las siguientes imágenes.
Imagina que el alumno en la imagen camina por una recta inclinada. Posiciona la misma en el plano cartesiano y, si está caminando de izquierda a derecha ¿sobre qué eje del plano está caminando?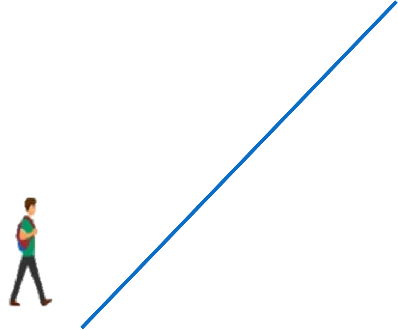
Si está caminando de izquierda a derecha, es decir, de manera horizontal, ese es el eje de las equis, también conocido como: el eje de las abscisas.
El eje de las equis es el nombre del eje del plano cartesiano, que corresponde a las distancias horizontales: el eje de las abscisas positivas. Sin embargo, se reconoce una particularidad.
Si se avanza sobre la recta inclinada, de izquierda a derecha, se está avanzando tanto de forma horizontal como de forma vertical. Es decir, se avanza en los ejes de las abscisas y de las ordenadas al mismo tiempo.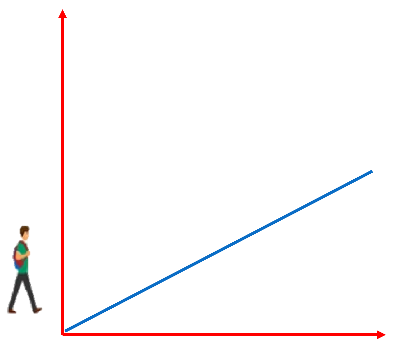
En la imagen se observa que, si la recta fuera más inclinada, la altura o la posición final recorrida en el eje de las ordenadas sería mayor que en el ejemplo anterior.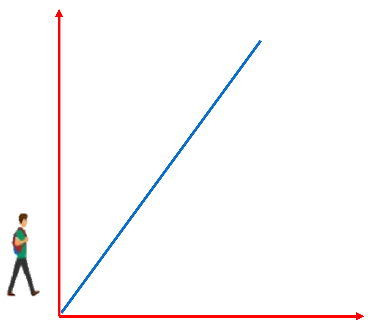
Pero ¿qué sucede con la pendiente en este caso?
Si la pendiente es la medida de inclinación de una recta, entonces la pendiente debe ser mayor al caso anterior.
Ahora, pasa al siguiente ejemplo.
Se tiene que la inclinación de la recta es menor ¿qué ocurre con la pendiente en este caso?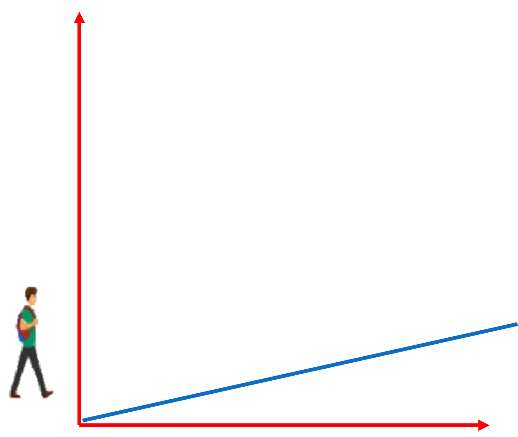
Que la pendiente es menor al caso anterior.
Si la pendiente mide la altura que avanza, entonces ¿la pendiente será siempre positiva?
Usa algunos ejemplos para comprobarlo.
En los casos anteriores observaste que la pendiente aumenta, por lo que se afirma que la pendiente será positiva cuando subas.
Sin embargo, imagina que se camina sobre una recta totalmente horizontal. En ese caso, la altura no aumenta, por lo que se refiere a un ejemplo de pendiente cero.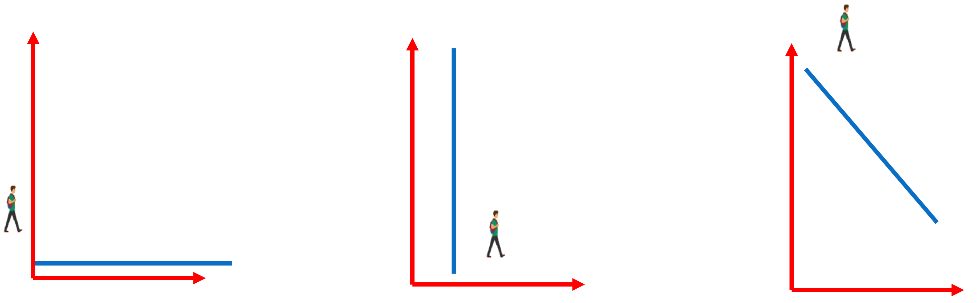
En otro caso, imagina una recta en completa vertical. En ese caso, se considera que la pendiente es infinita.
Y si caminas en una recta que tiene una inclinación, y que al ir avanzando de izquierda a derecha en vez de subir o aumentar tu altura, fuera disminuyendo la distancia hacia el eje de las abscisas, entonces se considera que la pendiente es negativa.
Sin embargo, son distintos conceptos ¿cómo se hace para tenerlos presentes?
Un alumno te ayudará a este respecto de un modo muy especial. - Video 2
https://youtu.be/1Hfas20aiU8
(del min. 5.13 al 6.19)
Se espera que con este rap queden más claros los tipos de pendientes, y cómo la posición de la recta es la que determina el valor que esta tendrá en su pendiente.
Se debe considerar que la pendiente es un valor numérico que se puede calcular, y para ello observa el siguiente ejemplo.
En el plano cartesiano se tiene una recta que, como ya se sabe, una línea recta se puede determinar por dos puntos: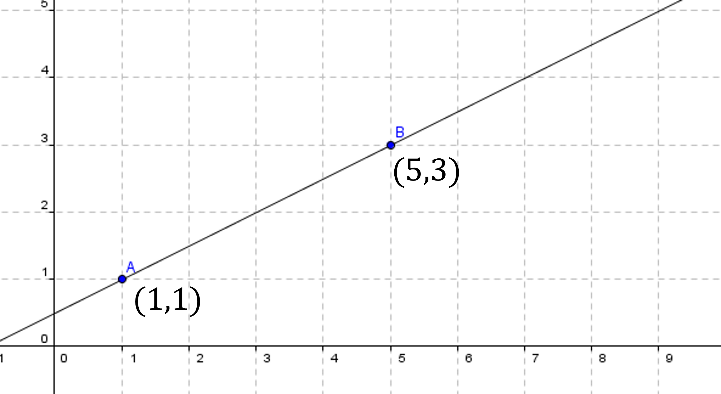
Sean A y B dos puntos en el plano
¿cuáles son las coordenadas de los puntos?
En cada punto, la primera entrada corresponde a la distancia en el eje horizontal, mejor denominado como eje de las abscisas. Mientras que la segunda entrada corresponde a la distancia en el eje vertical, el eje de las ordenadas, por lo que la coordenada del punto A corresponde a uno coma uno.
Y la coordenada del punto B es cinco coma tres.
De esta forma es como se denominan las coordenadas de los puntos en un plano cartesiano.
A continuación, se calcula la pendiente, es decir ¿qué tanto varía la distancia vertical conforme la distancia horizontal aumenta al desplazarse del punto A al punto B?
Para analizar la situación, se traza un segmento horizontal paralelo al eje de las abscisas, y un segmento vertical paralelo al eje de las ordenadas. Los dos segmentos permiten calcular la distancia entre los dos puntos, pero sólo lo que corresponde a cada eje.
Para calcular la distancia en el eje de las abscisas ¿qué datos se pueden utilizar?
Las cantidades que corresponden al eje de las abscisas de cada coordenada.
Se utiliza la primera entrada de cada coordenada. En el punto A es uno y en el punto B es cinco.
¿Y qué operación se utiliza para conocer la distancia entre las dos cantidades?
Para calcular la distancia entre el 5 y el 1, se buscar la diferencia entre ambas cantidades.
Lo mismo para la distancia sobre el eje de las ordenadas, sólo que ahora se obtiene la diferencia entre los valores que corresponden a la segunda entrada de cada coordenada.
Realiza las siguientes operaciones.
Después de realizar las operaciones, los resultados obtenidos son 4 en la distancia horizontal y 2 en la distancia vertical.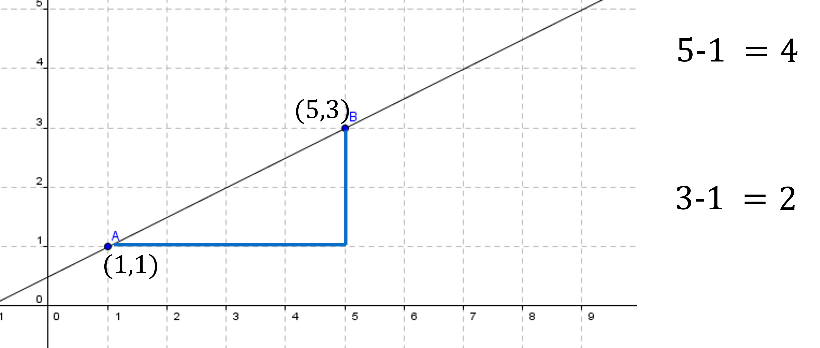
El siguiente paso es dividir el valor de la distancia vertical entre el valor de la distancia horizontal. El resultado es 2 entre 4, que se simplifica a 1 entre 2, y se representa con la letra “eme” minúscula.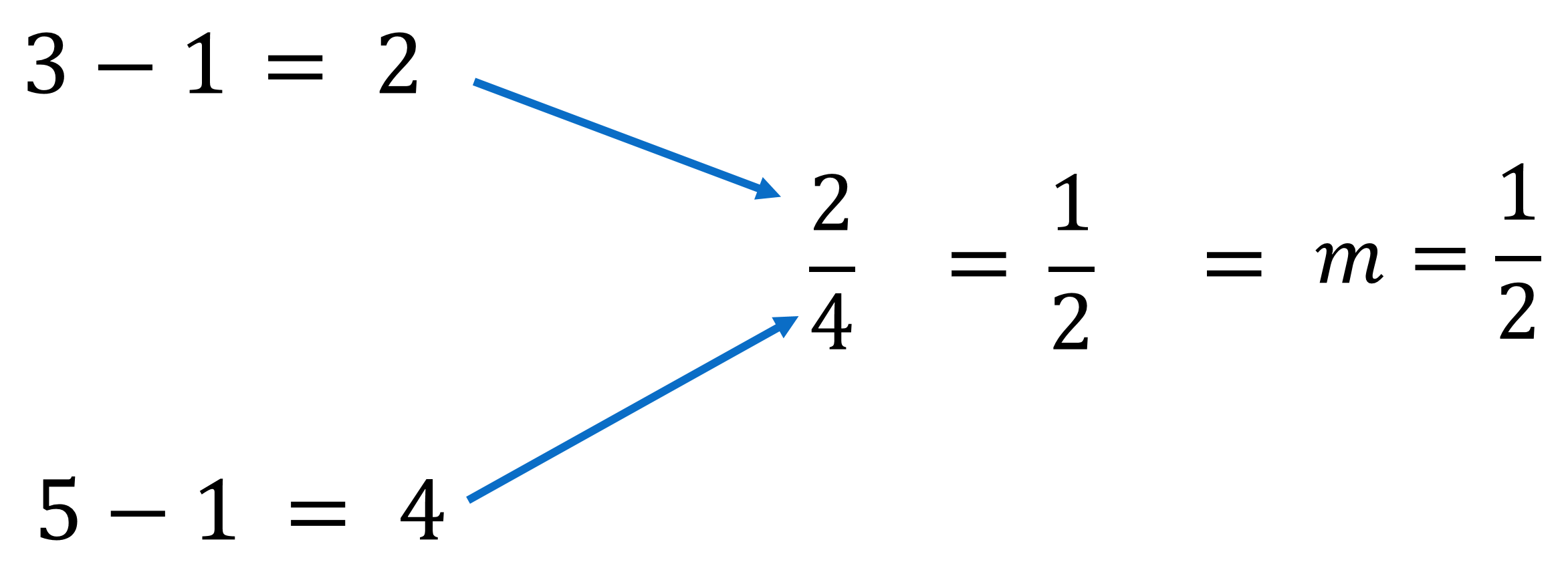
Este valor encontrado significa que el resultado de la pendiente sea de un medio y que por cada unidad que se mueva de izquierda a derecha, se debe mover la mitad de la unidad en el eje de las ordenadas.
El que una cantidad varíe con respecto a otra, es una razón de cambio. En este caso, es el resultado de dividir la diferencia en el eje de las ordenadas entre la diferencia en el eje de las abscisas.
A continuación, otro aspecto de esta situación.
Se puede ver que las rectas que se trazan, al unirse, forman un triángulo.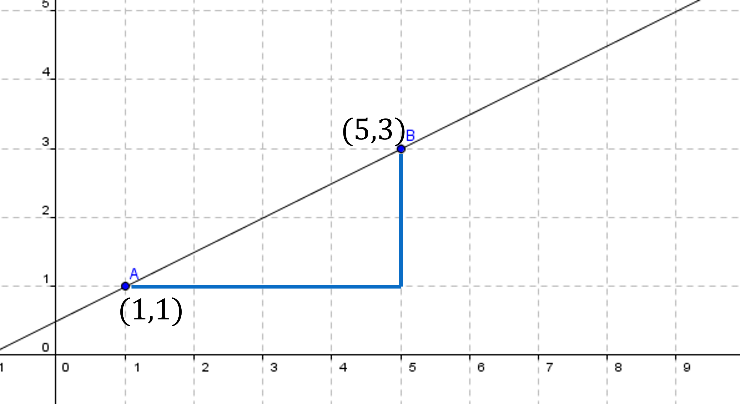
Si unes las dos rectas que se trazan para medir la inclinación de la pendiente, se genera un triángulo, pero no cualquier triángulo, sino un triángulo rectángulo.
Y como sabes, los lados de un triángulo rectángulo reciben un nombre en específico, son la hipotenusa y los catetos.
Atento al ángulo que se forma en el vértice donde se encuentran la hipotenusa y el cateto paralelo al eje de las abscisas.
Si observas con cuidado, se nota que los lados que se resaltaron, son los catetos tanto opuesto como adyacente.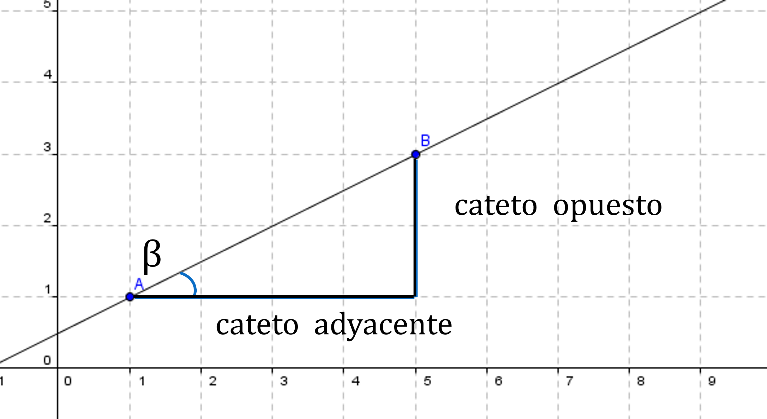
Pero ¿cuál es la fórmula para obtener la tangente de un ángulo?
La tangente de un ángulo se obtiene al dividir cateto opuesto entre cateto adyacente.
En otras palabras, el cateto opuesto es la distancia vertical, y el cateto adyacente la distancia horizontal.
Parece ser que utilizas la misma operación para obtener la pendiente que la operación que se realiza si quieres obtener la tangente.
Entonces, se puede afirmar que la pendiente de una recta es igual a la tangente del ángulo que la recta forma con una paralela, o con el propio eje de las abscisas o eje de las equis.
Dicho de otro modo: Si se obtiene el valor de la tangente del ángulo que la recta forma con el eje de las abscisas, se puede obtener la pendiente de una recta.
Resuelve los siguientes cuestionamientos, y ten a la mano tu calculadora científica.
Conociendo el ángulo teta que se forma al cortar el eje de las abscisas, que en este caso mide 40 grados ¿cómo se puede saber cuánto mide la pendiente de la recta que va del punto A al punto B?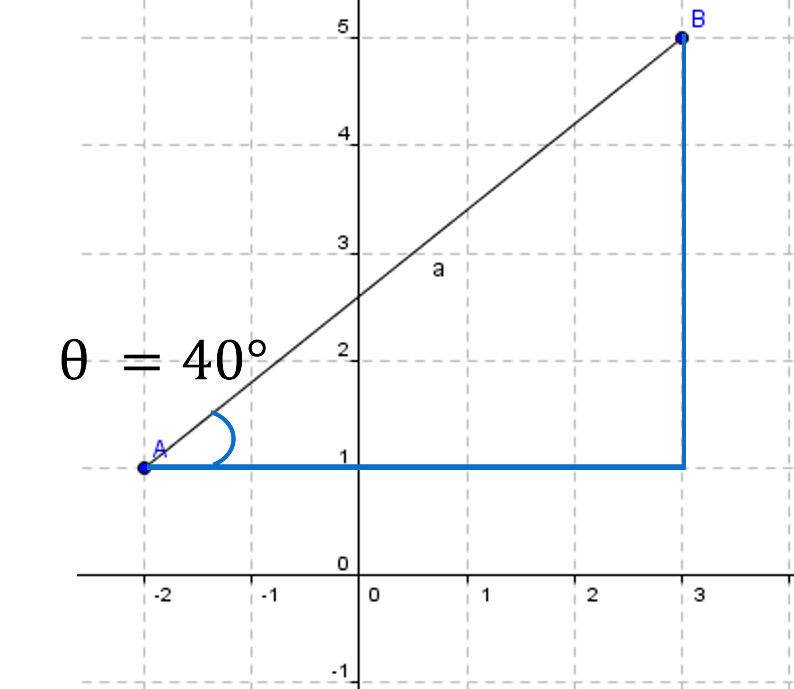
Utiliza tu calculadora científica, se busca el valor de la pendiente, que en este caso es la tangente de 40 grados.
El valor resultante es 0.8390 con muchos más decímales. Si se redondea a tres decimales, el valor resultante es cero punto ochocientos treinta y nueve.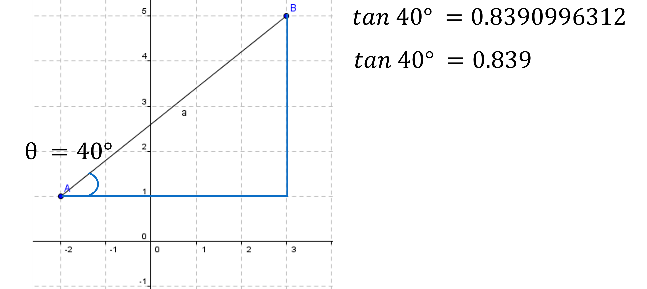
El uso de la calculadora científica resulta útil para encontrar la tangente de un ángulo. Sin embargo, ¿se puede calcular el valor de la tangente, conociendo el desplazamiento horizontal y el desplazamiento vertical?
Resuélvelo de la forma que mejor sepas hacer, puede ser mediante la resolución de problemas. Observa un ejemplo para ello.
Hace unos años, cuando visité la Ciudad de México, me encontré con uno de los monumentos característicos de la ciudad: ¡El ángel de la independencia!, y tomé esta foto.
En ese momento, se restauraba el monumento, y para tomar la foto, me acomodé junto a una grúa con un cable que sostenía la cima del ángel hasta mi costado.
Yo me encontraba a 60 metros de la base. No les diré el ángulo de inclinación que formó el cable, sin embargo, le pregunté al operador de la grúa y lo anoté en este sobre.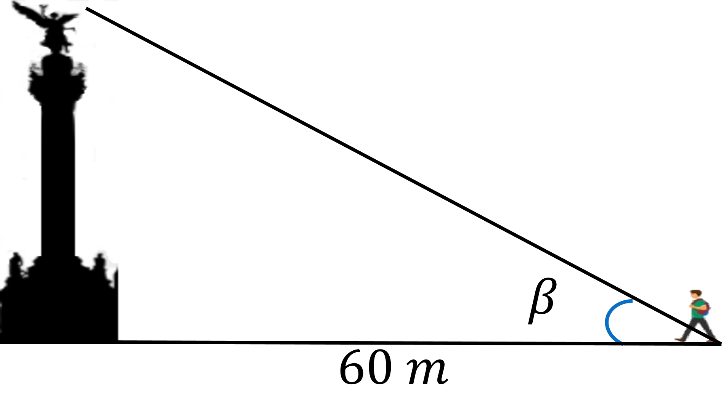
Realiza el ejercicio:
La altura del monumento son 45 metros. Con esta información, se necesita conocer el ángulo de inclinación del cable de la grúa.
Entonces, analiza los datos.
Como se reconoce, hay un triángulo, pero cualquier triangulo sino un triángulo rectángulo.
Lo que se quiere encontrar es el valor del ángulo de inclinación. Le llamarás beta.
La altura de la estructura, que, para este caso, será el cateto opuesto.
Y la distancia del que tomó la foto, es el cateto adyacente.
El siguiente punto consiste en saber qué función trigonométrica es posible utilizar.
Para la función son útiles el cateto opuesto y el cateto adyacente. Esta fue la función tangente.
Entonces, lo siguiente es calcular la tangente de beta.
Y la igualdad queda de la siguiente forma
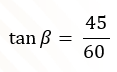
Observa cómo se han sustituido los valores que se conocen.
Al realizar la división del cateto opuesto sobre el cateto adyacente, el resultado que obtienes es 0.75 ¿Eso quiere decir que el ángulo mide 75 grados?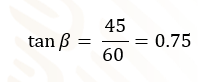
Es común pensar eso, pero el valor 0.75 es la tangente del ángulo, no el ángulo.
Para obtener el valor del ángulo, se utiliza la calculadora científica.
El procedimiento depende del modelo de esta. Sin embargo, la mayoría de las calculadoras tienen un pequeño botón como el que se muestra en pantalla, SHIFT, que permite usar las funciones secundarias de cada botón.
La secuencia SHIFT más tan, deja como resultado la función tan a la menos uno, que es la función recíproca de la tangente. Esto da como resultado el ángulo del que tienes su valor tangente.
Y el resultado final mostrado es aproximadamente de 36.86
El ángulo en cuestión medía 36.86 grados.
Con el uso correcto de las funciones trigonométricas se ha resuelto el problema.
Si no cuentas con una calculadora científica puedes emplear las tablas de equivalencias trigonométricas, que están en tu libro de tercero de secundaria, y que son iguales de útiles y confiables.
Este ejercicio fue óptimo para practicar las funciones trigonométricas. Sin embargo, las aplicaciones para la función tangente de un ángulo no se detienen ahí. En el siguiente video del inicio al minuto 04:18, se explica otras de las aplicaciones de las funciones trigonométricas. - Construcción de rampas de acceso y carreteras
https://www.youtube.com/watch?v=CwAeubih9nk&feature=youtu.be
En el video se utilizó la misma relación que se empleó durante la sesión para establecer el ángulo de inclinación de las rampas. Es decir, la altura que se denominó cateto opuesto, y la distancia horizontal que se nombró cateto adyacente.

Y en este caso, se calcula la pendiente de la rampa se utiliza la misma fórmula.
Resuelve el siguiente ejercicio:
Al inicio se dijo que una recta que se encuentra totalmente de forma vertical, el valor de su pendiente es el infinito.
¿Por qué es así? Como sugerencia, utiliza la definición de pendiente de una recta.
Para recapitular la sesión, se aprendió que el uso de la tangente en triángulos rectángulos ayuda a calcular distancias inaccesibles.
También existe una relación de igualdad entre el valor de la pendiente de una recta con la tangente del ángulo que forma la recta con el eje de las abscisas.
El reto de hoy:
Investiga en tu libro de texto el tema y resuelve nuevos problemas con el propósito de consolidar lo aprendido.
En caso de no contar con calculadora científica, puedes consultar tus libros de tercero de secundaria, mostradas en el índice como tablas de funciones trigonométricas.
¡Buen trabajo!
Gracias por tu esfuerzo.
