Pendiente. Problemas reales
Pendiente. Problemas reales
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: resolver problemas reales usando la tangente y la fórmula de la pendiente.
¿Qué vamos a aprender?
Para iniciar reflexiona la siguiente pregunta:
¿Qué es la razón de cambio entre dos cantidades que están relacionadas?
Una manera de definir la razón de cambio es el incremento o decremento de una cantidad respecto al incremento o decremento de otra; cuando ambas están relacionadas entre sí, se puede representar gráficamente como una recta y se observa en su pendiente “m”.
También se conoce que la pendiente “m” de una recta es igual a la tangente del ángulo de inclinación alfa de la recta.
Cuando no se sabe el valor del ángulo de inclinación “alfa” de la recta, es posible calcular el valor de la pendiente “m”. Si se conocen dos puntos pertenecientes a la recta, es decir, “m” es igual a “y2”, menos “y1”, entre “x2”, menos “x1”.
¿Qué hacemos?
Se analizan de forma práctica las características y el cálculo de la pendiente a través del siguiente ejercicio.
Una vela tiene una altura inicial de 10 centímetros, 30 minutos después de haber sido encendida; su altura es de 7 centímetros.
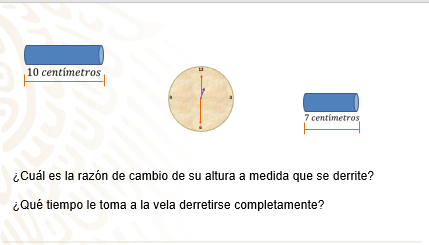
Se realiza el trazo de la gráfica que representa el problema para contemplar los datos y las características de la pendiente.
En el eje de las abscisas o “x” se grafica la duración del tiempo de la vela encendida.
En el eje de las ordenadas o “y” se grafica la altura de la vela conforme se va consumiendo.
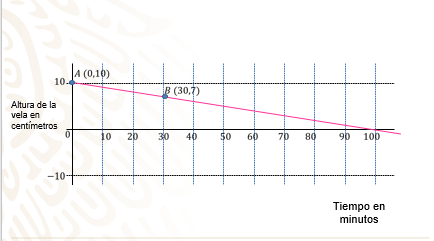
El primer punto para graficar es (0, 10), porque “0” es el instante en que se enciende la vela y mide 10 centímetros de altura inicial.
El segundo punto para graficar es (30, 7), es decir, transcurridos 30 minutos, la vela tiene una altura de 7 centímetros.
Como la altura de la vela está en función del tiempo que permanece encendida, se prolonga la recta para analizar el comportamiento de la vela.
La razón de cambio entre la altura y el tiempo que permanece encendida la vela es la pendiente de la recta.
Como se conocen dos puntos de la recta, aplica en la fórmula de la pendiente de una recta y sustituye valores.
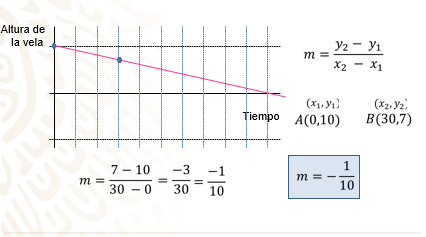
La pendiente es la diferencia entre “y2”, menos “y1”, entre “x2”, menos “x1”.
Las coordenadas son (0,10) y (30,7), entonces…
Es igual a 7, menos 10, entre 30, menos “0”.
Igual a 3 negativo entre 30.
Se simplifica la fracción, y la pendiente “m” de la recta es igual a un décimo negativo.
La pendiente obtenida es negativa, es decir, la recta desciende de izquierda a derecha.
La razón de cambio es la diferencia en la altura de la vela, entre la diferencia en el tiempo transcurrido.
Por lo tanto, la razón de cambio de la vela es que cada 10 minutos se consume o disminuye un centímetro de altura, un décimo de su altura.
Esto es, la pendiente es igual a un décimo negativo.
Para concluir el ejercicio, se analiza el tiempo que le toma a la vela derretirse totalmente.
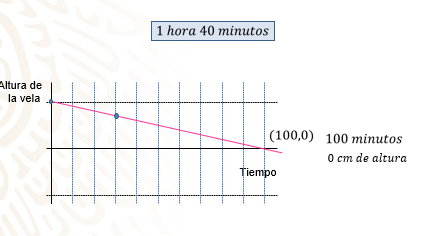
Observa la prolongación de la recta: ¿en qué punto corta al eje de las “x”?
Si tu respuesta fue “en el punto (100,0)” están en lo correcto, porque a los 100 minutos la vela tuvo “0” centímetros de altura.
Por lo tanto, el tiempo que tardó la vela en derretirse completamente fue 1 hora con 40 minutos.
Esto corresponde si se toma en cuenta que cada 10 minutos se consume un centímetro de altura. Es decir, se requieren 100 minutos para consumir 10 centímetros de la altura de la vela.
Hasta el momento, se obtuvo la pendiente conociendo dos puntos de la recta. Pero al inicio de la sesión se mencionó el poder calcular una pendiente por medio de la tangente del ángulo de inclinación de la recta.
Analiza el siguiente ejercicio para comprobarlo:
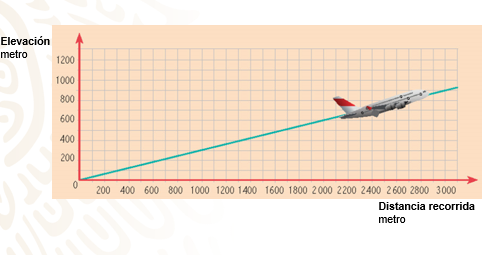
Con base en la gráfica, calcula el ángulo de inclinación de la trayectoria de ascenso del avión, la pendiente de la recta correspondiente y su ecuación.
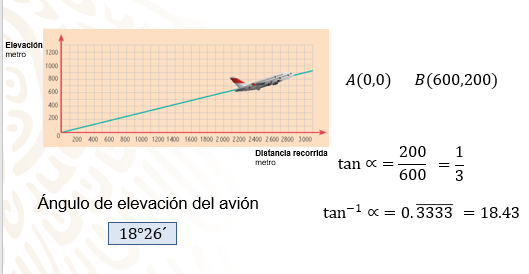
Para conocer el ángulo de inclinación de la trayectoria de ascenso del avión ubica dos puntos cualesquiera de la gráfica.
En este caso, se toman los puntos (0,0) y (600, 200).
La tangente del ángulo “alfa” es igual a cateto opuesto sobre cateto adyacente.
Se sustituye: tangente de “alfa” es igual a 200 entre 600.
Se simplifica, y la tangente de “alfa” es igual a 0.33 periódico.
En la calculadora, una vez colocada en modo sexagesimal (DEG), se elige la función “arco tangente”, representada con la tecla “tan” menos 1; se teclea la cantidad truncada 0.3333 y la tecla igual: el resultado es 18.43, que se puede expresar como 18 grados más 0.43 grados.
Cada grado consta de 60 minutos, por lo tanto, 0.43 grados es igual a 0.43 por 60 minutos. Esto es igual a 25.8 minutos, que se redondea a 26 minutos.
De este modo, una vez realizada la conversión a minutos, se tiene que la inclinación de la trayectoria de ascenso del avión es de 18 grados 26 minutos.
Ya se sabe que el avión tiene un ángulo de ascenso en su trayectoria de 18 grados 26 minutos.
Pero ¿cuál es la pendiente de la recta que representa la situación?
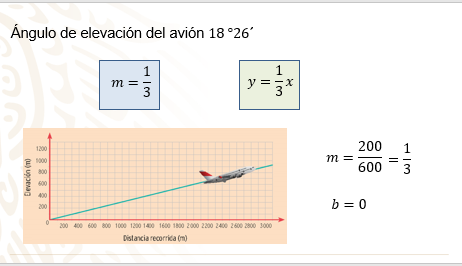
Como se sabe que la pendiente “m” de una recta es igual a la tangente del ángulo de inclinación de ésta, entonces “m” es igual a un tercio.
Comprueba este resultado empleando los dos puntos elegidos en la fórmula de la pendiente:
En este caso, “m” es igual a 200, menos “0”, entre 600, menos “0”.
Se simplifica y se obtiene un tercio, con lo que se confirma el razonamiento anterior.
¿Cuál es ahora la ecuación que representa la gráfica de la trayectoria del avión?
Para la ecuación de la recta de la forma “y” igual a “m,” por “x”, más “b”, “m” es igual a 1/3; y, en este caso, “b” es igual a “0” dado que la gráfica pasa por el origen.
Obtuviste la ecuación: “y” es igual a un tercio de “x”.
Calcula ¿qué tanto asciende el avión por cada unidad de distancia que recorre horizontalmente?
Es decir, ¿cuál es la razón de cambio entre la elevación y la distancia horizontal recorrida?

Se sabe que la razón de cambio es igual a la pendiente de la recta; si ésta es igual a 1/3, entonces:
Se sustituye en la ecuación:
“y” igual a un tercio por x.
“y” igual a 1 por (100) entre 3, igual a 33.33.
El avión asciende 33.33 metros por cada 100 metros recorridos.
Hasta el momento, se han resuelto ejercicios que implican una sola recta. Realiza un ejercicio más donde se conjuguen cuatro rectas.
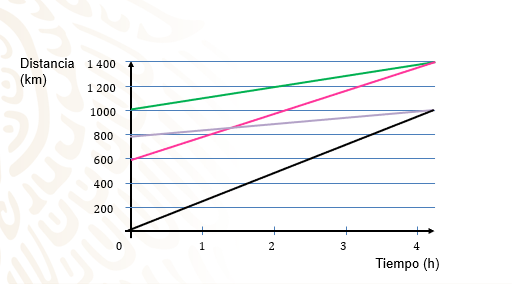
Cuatro trenes viajan con velocidad constante. Las rectas de la gráfica relacionan el tiempo transcurrido y la distancia que recorre cada tren.
Toma en cuenta que cada tren está representado con un color diferente.
Con la información anterior, se analizan las siguientes interrogantes:
Sin realizar cálculos, ¿de qué color es la recta que representa el tren más rápido?
¿De qué color es la recta que representa el tren más lento?
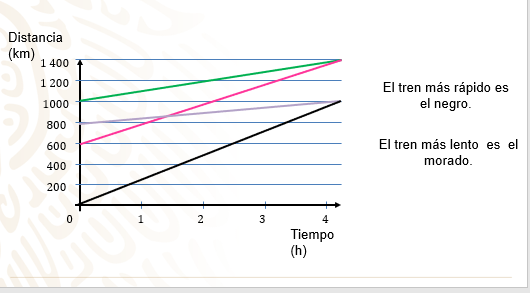
Al observar el ángulo de inclinación de cada una de las rectas en la gráfica, se puede decir:
Que el tren más rápido es el de color negro y el tren más lento es el de color morado.
A continuación, valida estos resultados con el cálculo de la pendiente de cada tren; los datos se obtienen de la gráfica.
Es decir, se obtiene el valor de dos puntos en cada recta para sustituirlos en la fórmula de la pendiente, la cual es igual a la diferencia entre “y2”, menos “y1”, entre “x2”, menos “x1”.
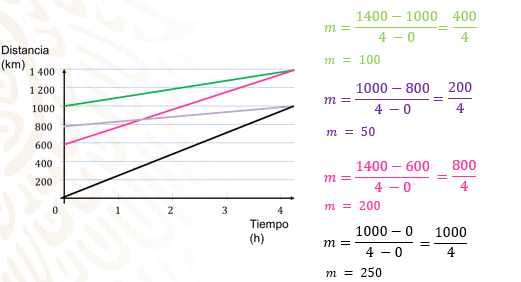
Todos los trenes viajan durante 4 horas, y la variante es la distancia que recorren en ese tiempo.
Al sustituir en la fórmula, para el tren verde la pendiente es 1 400, menos 1 000, entre 4, menos “0”, igual a 400, entre 4, igual a 100.
En el tren morado la pendiente es igual a 1 000, menos 800, entre 4, menos “0”, igual a 200, entre 4, igual a 50.
La pendiente del tren rosa es igual a 1400, menos 600, entre 4, menos “0”, igual a 800 entre 4, igual a 200.
La pendiente del tren negro es igual a 1 000, menos “0”, entre 4, menos “0”, igual a 1 000 entre 4, igual a 250.
Como se demostró, las pendientes son iguales a la velocidad de cada tren: el tren más rápido es el negro, con una velocidad de 250 km/h; y el tren más lento es el morado, con una velocidad de 50 km/h.
El siguiente ejercicio lo verás en el siguiente video del inicio al minuto 04:18. Anota en tu cuaderno las razones de cambio para cada ciudad, así como la ecuación de la recta para cada caso.
En la gráfica se muestra el precio de un viaje en taxi en relación con la distancia recorrida en una ciudad al norte de México a la que se llamara ciudad “A”.
- Ejemplos de razones de cambio significativas
https://youtu.be/p0bH22p47XM
La tarifa de los taxis no es igual en todas las ciudades.
Continúa observando el video, pero ahora del minuto 04:25 al 05:35. - Ejemplos de razones de cambio significativas
https://youtu.be/p0bH22p47XM
¿En dónde son más baratos los viajes en taxi?
Continua con el video del minuto 05:45 a 07:09. - Ejemplos de razones de cambio significativas
Anota en tu cuaderno las razones de cambio para cada ciudad. Compara las respuestas:
Para la ciudad “A”, la razón de cambio fue 16 pesos por kilómetro, mientras que para la ciudad “B” fue de 12 pesos por kilómetro.
Si se expresa la pendiente en términos de pesos por metro, la ecuación de la recta para la ciudad “A” es: “y” igual a “0.016x”, y la ecuación para la ciudad “B” es: “y” igual a “0.012x” más 12.
Verifica si tus respuestas coinciden con las anteriores.
Observa un nuevo ejercicio.
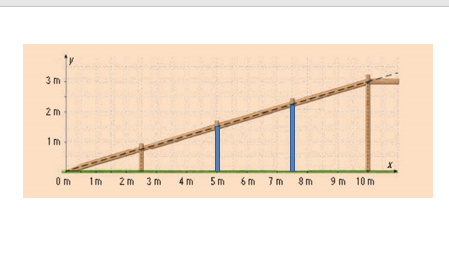
En la imagen se muestra el esquema de la rampa que se construirá en la central de abastos para facilitar el traslado de mercancía.
Antes de construir la rampa es necesario saber qué altura debe de tener el poste a la mitad de la rampa. Además, qué altura debe de tener el poste a tres cuartos de la longitud de la rampa.
Anota los datos necesarios para que resuelvas este ejercicio en tu cuaderno.
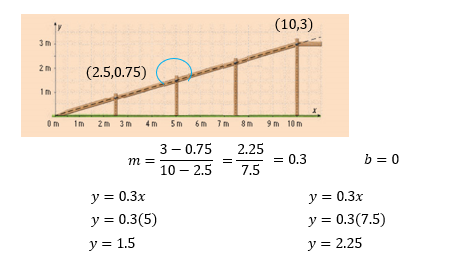
Con sólo observar la gráfica, ¿se puede saber la altura del poste a 5 metros de la base?
Se observa que el valor está entre 1 y 2 metros, pero ¿cómo se puede conocer el valor exacto?
Si respondiste que, con la ecuación de la recta, estás en lo correcto.
Por lo tanto, se debe obtener la pendiente de la recta. Los dos puntos conocidos son: (2.5, 0.75) y (10, 3).
Al sustituir se obtiene: “m” es igual a 3, menos 0.75, entre 10, menos 2.5.
Es igual a 2.25 entre 7.5, igual a 0.3.
Como ya se tiene el valor de “m”, ¿cuál es el valor de la ordenada al origen “b”?
Se sabe que la gráfica pasa por el origen, así que el valor de “b” es 0.
Anota la ecuación de la recta y sustituye el valor buscado de “x” igual a 5.
Esto lleva a decir que “y” es igual a 0.3, por 5, igual a 1.5. Entonces, la altura del poste a la mitad de la rampa es de 1.5 metros.
Y para la segunda pregunta, se realiza el mismo procedimiento para la altura del poste a 3/4 de longitud de la rampa:
“y” es igual a 0.3 por 7.5, igual a 2.25.
Se tiene como resultado que la altura del poste a tres cuartos de longitud de la rampa es de 2.25 metros.
Pero ¿a qué altura se asciende al subir la rampa por cada metro que se avanza en sentido horizontal? Es decir, ¿cuál es la razón de cambio entre la diferencia entre la altura y la diferencia entre los metros de la base de la rampa?
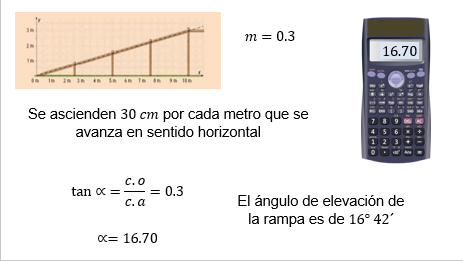
Se calcula la pendiente igual a 0.3, y la razón de cambio es igual a la pendiente de la recta.
Entonces, se ascienden 30 centímetros por cada metro que se avanza en sentido horizontal.
Encontraste la razón de cambio, pero falta por conocer el ángulo de inclinación de la rampa.
Ya se sabe que la tangente del ángulo “alfa” es igual al cateto opuesto sobre el cateto adyacente, es decir, a la pendiente. Ésta ya se conoce y es igual a 0.3.
Se usa la calculadora científica en modo “DEG” y en pantalla se tiene que el arco tangente de la pendiente 0.3 es igual a 16.70 redondeado, que se puede expresar como 16 grados más 0.70 grados.
Cada grado consta de 60 minutos, por lo tanto, 0.70 grados es igual a 0.70 por 60 minutos, igual a 42 minutos.
Una vez realizada la conversión a minutos, se tiene que el ángulo de elevación de la rampa es de 16 grados 42 minutos.
Realiza el último ejercicio de la sesión:
En un laboratorio se calentó un trozo de hielo durante 2 minutos, mostrando su comportamiento, como se observa en la gráfica.
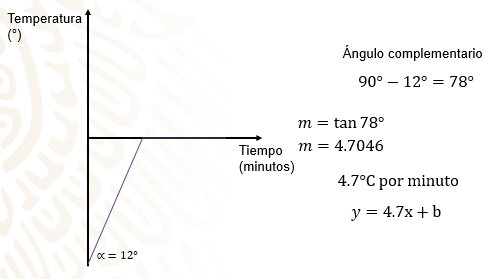
Sin embargo, no se tiene el registro de la temperatura del experimento, pero se cuenta con el ángulo de inclinación de la recta, que es de 12 grados en la parte inferior con respecto al eje “y”.
Con los datos de la gráfica no es posible determinar dos puntos de la recta para calcular la pendiente con la fórmula de razón de cambio, como se ha analizado hasta ahora, pero sí es posible calcular su valor a través de la tangente del ángulo.
Para la pendiente del ángulo se debe considerar el ángulo complementario de 12 grados porque es el ángulo de la pendiente con la horizontal. Es decir, 90 grados menos 12 grados, igual a 78 grados.
Siguiendo la fórmula de la pendiente, es igual a la tangente de 78 grados, igual a 4.7046.
Si se obtiene este resultado es porque se realizó el cálculo de la pendiente por medio de la tangente del ángulo.
Después, con este cálculo, es posible determinar el valor de la temperatura a través del tiempo por medio de la ecuación que relaciona a las dos variables.
Si se considera a la temperatura como la variable “y” y al tiempo como la variable “x”, por tratarse de una recta con pendiente igual a 4.7 se sustituye en la expresión general de una recta que pasa fuera del origen y se obtiene: “y” igual a “4.7x” más “b”.
El reto de hoy:
Plantea un problema donde se requiera calcular el ángulo de elevación.
La pendiente de una recta brinda información para interpretar o analizar las variables involucradas, pues tal como decía Aristóteles: “La inteligencia consiste no sólo en el conocimiento, sino también en la destreza de aplicar los conocimientos en la práctica”.
Aplica lo analizado durante la sesión.
Busca en tu libro de texto todo lo relacionado con este tema y resuelve los ejercicios que ahí se proponen para enriquecer tu conocimiento.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas