Multiplicación y división de fracciones y números decimales
Aprendizaje esperado: resuelve problemas de multiplicación y división con fracciones y decimales positivos.
Énfasis: obtener los factores escalar y recíproco.
¿Qué vamos a aprender?
Profundizarás en la resolución de problemas de multiplicación y división de fracciones y números decimales.
¿Qué hacemos?
Analiza el siguiente problema de multiplicación:
Problema de multiplicación con números fraccionarios y decimales.
Imagina que tienes que diseñar una zona de juegos en el siguiente terreno, y necesitas conocer la medida del área para saber que juegos puedes comprar.
Las medidas del terreno son las siguientes:
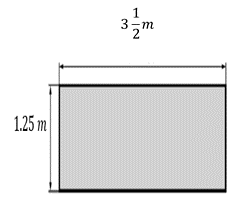
¿Cuál será la medida del área del terreno? Observa cómo puedes calcularla.
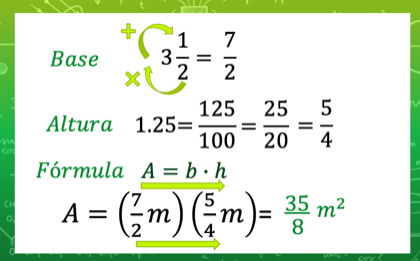
Primero, tienes que convertir 3½ a fracción impropia. Como sabes, el 2 multiplica al 3 y se le suma 1, lo que da como producto 7/2.
Luego, convierte el número decimal, en este caso 1.25, a fracción, para operar con fracciones.
Escribe el 125 en el numerador y se divide entre 100, porque tienes dos cifras a la derecha del punto decimal, es decir, centésimos.
Después, simplifica la fracción 125/100, en este caso. Le sacas la quinta parte al 125 y al 100, ya que 5 es divisor de ambos, y queda la fracción 25/20.
Posteriormente divide 25 y 20 entre 5 para simplificar la fracción a 5/4.
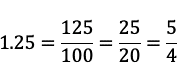
Toma en cuenta que la fórmula de un rectángulo se calcula de la siguiente manera:
A = b*h
Al multiplicar dos fracciones, multiplicas numerador por numerador y denominador por denominador.
Así sabrás que el área del terreno es igual a 35/8 de metros cuadrados.
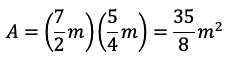
Al final, puedes convertir el resultado a número mixto o número decimal. Observa el ejemplo:
Ahora ya sabes cómo multiplicar una fracción por un número decimal.
El procedimiento para dividir números decimales entre fracciones, se puede aplicar a la solución del siguiente problema.
Problema de división con números fraccionarios y decimales.
Para confeccionar los sombreros de una obra de teatro, la vestuarista requiere cortar tramos de listón de 3/4 m de una pieza que mide 4.5 m de longitud. ¿Cuántos tramos de listón se obtienen de la pieza?
La operación que permite realizar un reparto equitativo es la división. En este caso, para conocer cuántos tramos de listón se obtienen, se divide 4.5 entre 3/4. Al igual que con la multiplicación, vas a operar con fracciones.
Primero convierte 4.5 a fracción decimal y se simplifica.
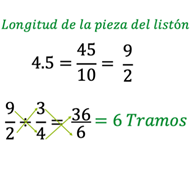
Ya que convertiste el número 4.5 a fracción decimal, divide las fracciones con las que cuentas. 9/2 entre 3/4.
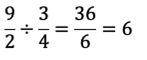
Se multiplica de manera cruzada. El numerador de la primera fracción por el denominador de la segunda fracción, y el producto se coloca en el numerador.
Ahora, multiplica el denominador de la primera fracción por el numerador de la segunda fracción y el producto se coloca en el denominador.
Obtienes 36 entre 6, y como 36 es divisible entre 6, procede a dividirlo, lo que te dará como resultado 6.
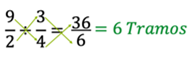
Por lo tanto, puedes concluir que el resultado de 4.5 entre 3/4 es igual a 6. Es decir, se obtienen 6 tramos de esa pieza de listón, todos con la misma medida.
Ahora que ya sabes cómo resolver problemas de multiplicación y división de números fraccionarios con decimales, resuelve el siguiente ejercicio.
Problema de decimales con fracciones.
El diseño de los recipientes que se muestran en la siguiente figura aprovechan el espacio de almacenamiento, ya que cuando están vacíos pueden guardarse uno dentro de otro.

Si el recipiente 2 tiene un tamaño proporcional de 3/4 respecto al recipiente 1. ¿cuánto mide su diámetro?
Primero, se convierte el número decimal, en este caso 22.5 a fracción, para operar con fracciones.
Escribe el 225 en el numerador y lo divides entre 10, porque tienes una cifra a la derecha del punto decimal, es decir, décimos.
Después, simplifica la fracción 225/10. Le sacas la quinta parte al 225 y al 10, ya que el 5 es divisor de ambos, y queda la fracción 45/2.
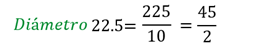
Finalmente, multiplica las fracciones para obtener el resultado del diámetro. Al multiplicar dos fracciones, se lleva a cabo el producto de numerador por numerador y denominador por denominador.
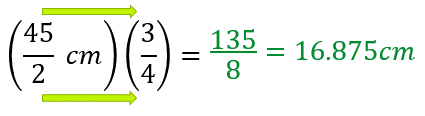
Ya que calculaste el diámetro, realiza las operaciones necesarias para conocer cuál será su altura.
Como en el desarrollo de la primera operación que realizaste en este problema. Primero, convierte el número decimal, en este caso 12.7 a fracción, para operar con fracciones.
Escribe el 127 en el numerador y se divide entre 10, porque tienes una cifra a la derecha del punto decimal, es decir, décimos.

Para concluir con la altura, multiplica las fracciones que corresponden. Al multiplicar dos fracciones, se lleva a cabo el producto de numerador por numerador y denominador por denominador.
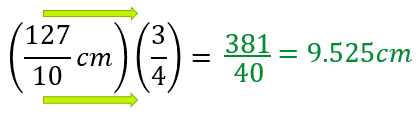
Ahora ya sabes cómo realizar las operaciones necesarias para multiplicar y dividir decimales con fracciones.
El reto de hoy:
Si tuvieras que trazar el terreno del problema de “multiplicación con números fraccionarios y decimales” a escala, ¿qué información debes considerar?, ¿qué características debe tener su trazo comparado con el terreno original?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/
