Multiplicación de números positivos y negativos
Aprendizaje esperado: resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos.
Énfasis: la regla de los signos de la multiplicación de números enteros y el plano cartesiano
¿Qué vamos a aprender?
Ampliarás tus conocimientos de la multiplicación de números positivos y negativos e identificarás las reglas de los signos en la multiplicación.
En la sesión anterior, profundizaste en las multiplicaciones de números enteros con base en las sumas iteradas y utilizaste los números positivos y negativos para representar las ganancias y pérdidas en diversos ejemplos. También, conociste el resultado de multiplicar dos números positivos y un número positivo por uno negativo.
Ahora aprenderás a resolver multiplicaciones de números positivos y números negativos, pero en esta ocasión lo realizarás para representar movimientos: avances y retrocesos.
¿Qué hacemos?
Para iniciar, retomarás algunos temas de la sesión anterior. De acuerdo con los conocimientos que adquiriste, responde las siguientes preguntas:
¿Qué sucede al multiplicar un número negativo por un número positivo?
¿Qué tipo de número tendrá el producto de estas multiplicaciones?
¿Qué sucederá al multiplicar dos números negativos?
Para corroborar tus respuestas, utilizarás la siguiente recta numérica que simula el desplazamiento de un móvil, tal como se muestra en las siguientes imágenes.
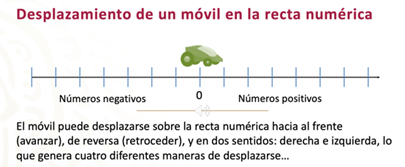
Ya que conoces los desplazamientos que puede realizar el móvil, analiza en qué consiste cada uno.
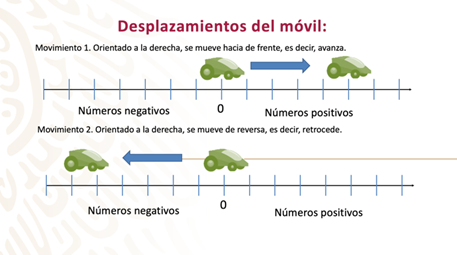
Movimiento 1:
El móvil se coloca en el cero orientado hacia la derecha (hacia los números positivos) y se mueve al frente, es decir: avanza. Con este desplazamiento, cuando el móvil se detiene, queda ubicado sobre los números positivos.
Movimiento 2:
El móvil se vuelve a colocar en el cero, orientado a la derecha, y se mueve en reversa, es decir, retrocede. Este desplazamiento hace que, cuando el móvil se detenga, quede ubicado sobre los números negativos.
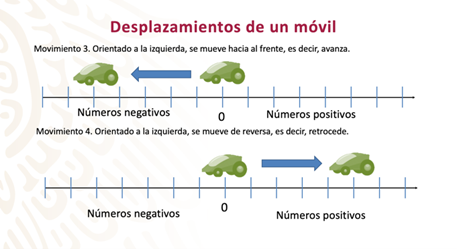
Movimiento 3:
El móvil se coloca en el cero, pero en esta ocasión orientado a la izquierda (hacia los números negativos) y se mueve hacia el frente, es decir, avanza. Con este desplazamiento el móvil se ubicará sobre los números negativos cuando se detenga.
Movimiento 4:
Finalmente, el móvil se coloca orientado a la izquierda y se mueve en reversa, es decir, retrocede. Este desplazamiento hace que el móvil quede sobre los números positivos después de detenerse.
Ahora que ya conoces los desplazamientos del móvil, los utilizarás para representar y justificar los resultados de multiplicar números positivos y negativos.
Reflexiona en el movimiento 1 y 2.
En el movimiento 1. El móvil está en cero, orientado a la derecha y se desplaza 3 veces, avanzando 2 unidades en cada desplazamiento.
¿A qué número llega el móvil?
¿Qué signo tiene ese número?
¿Con qué multiplicación se puede representar la situación?
Al moverse hacia la derecha tres veces, dos unidades en cada desplazamiento, el móvil queda situado sobre el número: seis positivo.
Este movimiento puede representarse con la multiplicación:
(+3) (+2) = (+6)
Recuerda que los números positivos pueden considerarse como “avances” y los números negativos, como “retrocesos”.
En el movimiento 2. El móvil está en el cero, orientado hacia la derecha y se mueve de reversa tres veces dos unidades, en cada movimiento.
¿A qué número llega el móvil?
¿Qué signo tiene ese número?
¿Con qué multiplicación podemos representar la situación?
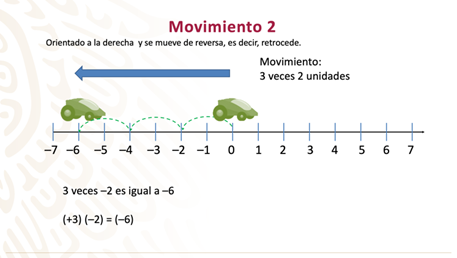
Al realizar los movimientos mencionados, se observa que el móvil queda sobre el número: seis negativo.
Este movimiento se puede representar con la multiplicación:
(+3) (–2) = (–6)
En las operaciones anteriores (movimiento 1 y 2), el tipo de número o el signo de cada factor, están determinados por la orientación y el movimiento del móvil. Observa la siguiente imagen.
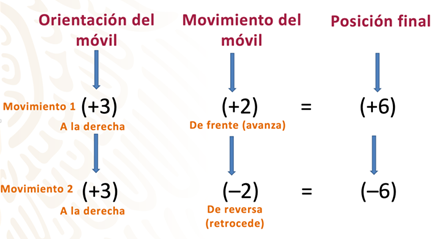
El primer factor de cada multiplicación está determinado por la orientación del móvil, es decir, si el móvil está orientado hacia la derecha, el primer factor es un número positivo, pero si estuviera orientado hacia la izquierda, el factor es un número negativo.
El segundo factor está determinado por el movimiento del móvil: si el desplazamiento es hacia el frente, el factor es un número positivo, pero si es de reversa, entonces el número es negativo.
Las reglas anteriores, permiten justificar las multiplicaciones que se realizaron para representar los dos primeros movimientos del móvil.
Reflexiona en el movimiento 3 y 4.
Analiza lo siguiente:
Considerando que el móvil se desplaza 3 veces 2 unidades, en cada uno de estos movimientos:
¿En qué número quedaría el móvil en cada caso?
¿Qué multiplicación representaría cada movimiento?
¿Cuál sería el resultado de cada multiplicación?
Observa que sucede en estos movimientos (3 y 4).
En el movimiento 3. El móvil se desplaza nuevamente 3 veces 2 unidades, en cada desplazamiento.
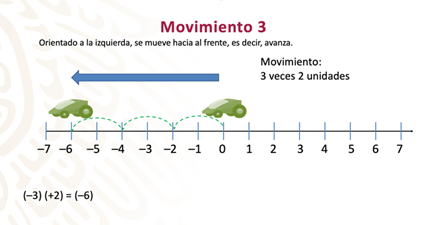
De acuerdo con las reglas anteriores, como el móvil está orientado hacia la izquierda, el primer factor de la multiplicación es un número negativo y el segundo, un número positivo, porque el móvil avanza.
Entonces, la multiplicación que representa el movimiento es:
(–3) (+2) = (–6)
Si se comparan los movimientos 2 y 3, en ambos casos el móvil quedó en el número –6.
Por lo tanto, se puede afirmar que:
(+3) (–2) es igual a (–3) (+2) = (–6)
Entonces, se puede decir que al multiplicar un número negativo por un número positivo el resultado es igual a un número negativo:
(–)(+) = (–)
En el movimiento 4. Nuevamente el móvil se desplaza tres veces dos unidades, en cada movimiento.
De acuerdo con las características de este movimiento, como el primer factor de la multiplicación está determinado por la orientación del móvil, y como en este caso, es hacia la izquierda, entonces el primer número es negativo, es decir, –3. El segundo factor es –2, porque el móvil se mueve de reversa.
Ya que se tienen los dos factores y la posición final del móvil, la multiplicación se representa de la siguiente manera:
(–3) (–2) = (+6)
Por lo que, se puede afirmar que, al multiplicar dos números negativos, el resultado es un número positivo.
Es decir:
(–) (–) = (+)
Ya que comprendiste los cuatro movimientos del móvil con multiplicaciones de números enteros positivos y negativos. Ahora, resuelve los siguientes ejercicios relacionados con el mismo caso (recta numérica del móvil):
Actividad 1.
Lee los siguientes ejercicios, y resuélvelos.

Concluye la actividad, verificando tus resultados con las rectas numéricas de la siguiente imagen.
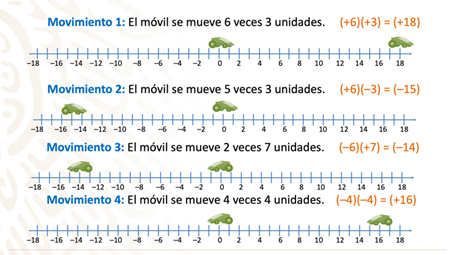
A estos criterios se les conoce como: reglas de los signos de la multiplicación. Y se pueden simplificar de la siguiente manera:

A continuación, resolverás un problema en el que se aplica la multiplicación de números positivos y negativos.
Problema: Descenso de la temperatura.
En una ciudad, la temperatura era de 8º Celsius a las 10 de la noche. A partir de esa hora la temperatura empezó a descender en promedio 3º Celsius cada hora, es decir –3º Celsius, durante las siguientes siete horas.
¿Cuál era la temperatura en la ciudad a las 5 de la mañana?
¿Cómo se puede establecer cuantos grados descendió la temperatura?
¿Qué operaciones permiten obtener la temperatura a las 5 de la mañana?
Se utilizará nuevamente la recta numérica para resolver el problema, como en la simulación con el movimiento del móvil.
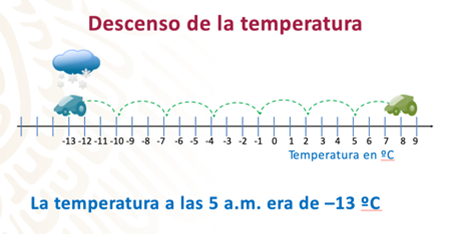
El móvil se coloca en 8 grados Celsius, porque es la temperatura inicial del problema y se mueve de frente, hacia la izquierda, 7 veces 3 unidades en cada movimiento, porque ese valor corresponde al descenso promedio de la temperatura cada hora.
Por lo que, la temperatura en el lugar, después de siete horas, es decir, a las 5 de la mañana, era de –13º Celsius.
Para resolver aritméticamente esta situación, observa la siguiente imagen.
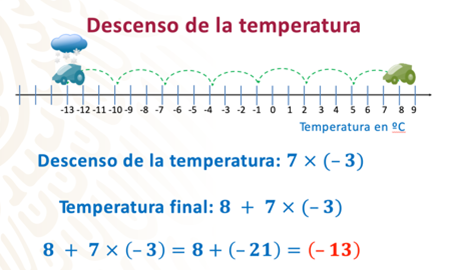
La multiplicación que representa el descenso de la temperatura es 7 positivo por 3 negativo, porque la temperatura se movió –3 grados siete veces, pero para resolver el problema también se tiene que considerar la temperatura inicial, es decir: 8 grados Celsius.
Por lo anterior, la operación que resuelve el problema es:
8 + 7 x (-3)
No olvides aplicar la jerarquía de operaciones, la cual indica que primero se multiplica y después se suma.
Positivo por negativo es igual a negativo, entonces 7 por 3 negativo es igual a 21 negativo.
Después a 8 se le suma el resultado anterior, 8 más 21 negativo es igual a 13 negativo.
8 + (-21) = -13
El resultado de la operación coincidió con la representación gráfica.
Ahora, observa la siguiente situación y pon atención en cómo resolvió Angélica la adivinanza.
La adivinanza de Ana:


La comprobación del resultado dice: Como negativo por negativo es igual a positivo, entonces, –4 por –6 es igual a 24 y 24 más 3 es igual a 27.
Con el trabajo de esta sesión, aprendiste que existen criterios que deben aplicarse al multiplicar números positivos y negativos.
Si tienes dudas sobre la multiplicación de números positivos y negativos, o si quieres practicar, revisa tu libro de texto y resuelve las actividades correspondientes a este tema.
El reto de hoy:
Resuelve el siguiente problema:
Considera el movimiento 3.
Si el móvil se mueve 4 veces y llega al número –32,
¿De cuántas unidades fue cada movimiento?
¿Qué operación permite representar la situación?
¿El resultado de la operación es un número positivo o negativo?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: