Multiplicación de números fraccionarios y decimales positivos y negativos

Multiplicación de números fraccionarios y decimales positivos y negativos

Aprendizaje esperado: resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos.

Énfasis: dar sentido y significado a la multiplicación de números fraccionarios y decimales positivos y negativos.

¿Qué vamos a aprender?

Continuarás avanzando en el estudio de las estructuras multiplicativas de los números positivos y negativos. En esta sesión, profundizarás y darás significado a la multiplicación de números fraccionarios y decimales.

¿Qué hacemos?

Para iniciar, analiza el siguiente acertijo:

¿Cuándo el triple de un número es negativo?

Para resolver este acertijo debes recordar el significado de obtener el triple de un número. El triple de un número es multiplicar por tres.

Entonces, se puede traducir la pregunta en una expresión matemática como la siguiente, tres por un número desconocido “x”, deberá ser menor que cero, ya que un número menor que cero es negativo.

3 (x) < 0

Pero ¿cuáles son esos números que hacen válida la expresión? es decir, cuáles son los valores que puede tomar “x”.

Al cuestionar a tres estudiantes sobre los posibles números que puede tomar “x”, contestaron lo siguiente:

Teresa indicó que puede ser 7, Jorge dijo que 0 y Elena sugirió que -5.

• Teresa: 7
• Jorge: 0
• Elena: -5

¿Quién de los tres está en lo correcto? y ¿por qué?

Analiza cada una de las soluciones que dieron las alumnas y el alumno en cuestión.

3 (x) < 0

Teresa indicó que podía ser siete. Al sustituir el número siete en equis, se obtiene:

3 (x) = 3 (7) = 21 > 0

Al multiplicar el número positivo “tres” por otro positivo “siete”, el producto también es positivo “veintiuno”. De lo anterior se puede deducir que la respuesta del acertijo, no puede ser un número positivo.

Ahora analiza la respuesta de Jorge. Él dijo que podía ser cero. Al sustituir cero en la expresión se tiene lo siguiente:

3 (x) = 3 (0) = 0

Por lo tanto, tampoco puede ser cero la respuesta del acertijo.

Elena sugirió como una posibilidad el número -5. Analiza lo que ocurre cuando se sustituye en la expresión a este número.

3 (x) = 3 (-5) = -15

Recuerda que es 3 por -5; es decir, esta multiplicación se puede interpretar como la suma repetida:

(-5) + (-5) + (-5) = -15

Lo anterior quiere decir que, al multiplicar el número positivo “tres” por el negativo “menos cinco” se obtiene al número negativo “menos quince”. Por ello, cuando “x” es igual a “-5” se cumple que el triple de ese número es negativo, esto quiere decir que Elena dio una de las soluciones del acertijo.

Reflexiona acerca de los productos que has obtenido: cómo deben ser los factores para que un producto sea negativo.

De acuerdo con lo anterior, has recuperado tres aspectos importantes que debes tomar en cuenta cuando resuelves una multiplicación:

• Al multiplicar dos números positivos el producto es también un número positivo.
• Al multiplicar un número positivo por cero, el producto es cero.
• Al multiplicar un número positivo con otro negativo, el producto es negativo.

Ya identificaste una de las soluciones que tiene el acertijo, pero ¿tendrá otras soluciones?, ¿cuáles serán?

Compartiendo el acertijo con más estudiantes, Pablo, Jimena y Salvador, quienes han identificado otras opciones, indicaron lo siguiente:

• Pablo dice que todos los números enteros negativos son solución del acertijo.
• Jimena dice que todos los números decimales negativos cumplen con la condición del acertijo.
• Y Salvador indica que todos los números fraccionarios negativos son parte de la solución del acertijo.

Analiza lo que respondió cada estudiante.

Pablo dice que todos los números enteros negativos son solución del acertijo, es decir, que al multiplicar tres por un número entero negativo, el producto será negativo.

Para corroborar lo que Pablo menciona, toma tres números enteros negativos y sustitúyelos en la expresión: 3 (x). Resuelve la multiplicación y verifica si cumplen con la condición de que el producto sea un número negativo.

Utiliza los números: (-6), (-20) y (-100).

Si x = -6, 3 (x) = 3 (-6) = -18

Si x = -20, 3 (x) = 3 (-20) = -60

Si x = -100, 3 (x) = 3 (-100) = -300

Al sustituir los tres números enteros negativos, puedes observar que al multiplicar tres por algún número entero negativo, el producto siempre es negativo, por ello, se puede decir que Pablo está en lo correcto, el triple de cualquier número entero negativo es: negativo.

Ahora, reflexiona en la siguiente cuestión:

¿Sólo los números enteros negativos resuelven este acertijo?

Para resolver este cuestionamiento, analiza la respuesta de Jimena.

Ella dice que todos los números decimales negativos cumplen con la condición del acertijo. Recuerda que para que se cumpla la condición, el producto de tres por “x” debe ser un número negativo, es decir, menor que cero.

Para verificar si Jimena está en lo correcto, toma tres números decimales negativos y sustitúyelos en la expresión 3 (x). Resuelve la multiplicación y verifica si cumplen con la condición de que el producto sea negativo.

Considera como “x” a los números: (-0.1), (-2.4) y (-5.9).

Si x = -0.1, 3 (x) = 3 (-0.1) = -0.3

Si x = -2.4, 3 (x) = 3 (-2.4) = -7.2

Si x = -5.9, 3 (x) = 3 (-5.9) = -17.7

Al sustituir los tres números decimales negativos, se observa que al multiplicar tres por algún número decimal negativo, el producto siempre es negativo.

Analizado lo anterior, se puede decir que Jimena también está en lo correcto, el triple de cualquier número decimal negativo también es negativo.

Con lo anterior, ¿puedes predecir si la respuesta de Salvador será correcta?

Recuerda que Salvador dice que todos los números fraccionarios negativos son parte de la solución del acertijo, es decir, que el triple de un número fraccionario negativo es un número negativo.

Compruébalo. Determina: el triple de un tercio negativo, de cinco novenos negativo y de 17 veinticincoavos negativo.

Si x = -1/3, 3 (x) = 3 (-1/3) = –1

Si x = -5/9, 3 (x) = 3 (-5/9) = –15/9 = -5/3

Si x = -17/25, 3 (x) = 3 (-17/25) = –51/25

Entonces, también Salvador tiene razón.

De todo lo anterior puedes darte cuenta de que, el triple de un número, cuando éste es negativo, también su producto será negativo, sin importar si el número es entero, decimal o fraccionario.

Continúa con otro acertijo:

¿Cuándo el producto de, un quinto negativo por un número, tiene resultado positivo?

Para contestar, primero descifra la pregunta. Si se trata de un producto, quiere decir que, debes multiplicar factores, en este caso los factores son un quinto negativo y un número desconocido al que llamarás “x”.

Como el acertijo indica que, el resultado tiene que ser positivo, entonces el producto tiene que ser mayor que cero, ya que todos los números positivos son mayores que cero.

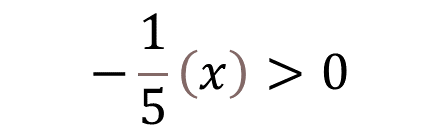
Entonces, debes encontrar un número desconocido que, al multiplicarlo por un número negativo, que en este caso es “un quinto negativo”, dé un número positivo como resultado.

Reflexiona, considerando las siguientes preguntas:

• ¿Qué tipo de número debe ser “x”?
• Y ¿cuántas soluciones puedes tener?

Analiza las posibilidades que tienes para determinarlo. Puedes sustituir números positivos, negativos o al cero y examinarlos.

Primero, considera en “x” al número positivo (0.3) y observa qué ocurre.

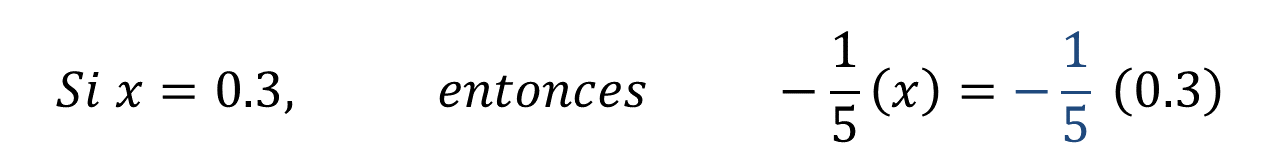
Para resolver la operación puedes convertir un quinto negativo a número decimal y multiplicar dos números decimales. Esto es:

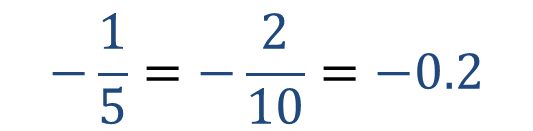
Ahora multiplica a dos décimos negativo con tres décimos positivo:

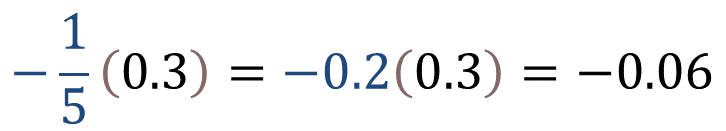
Entonces el producto es igual a seis centésimos negativo.

Otra forma de realizar la operación es utilizando la forma fraccionaria de estos dos números. Ahora convierte 0.3 a 3 décimos.

Resolviendo la multiplicación de estos números, tienes que un número negativo por otro positivo da un número negativo:

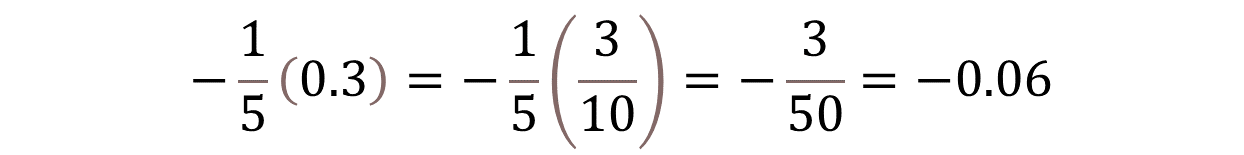
Obtienes como producto a tres cincuentavos negativo, que es equivalente a seis centésimos negativo, en su forma fraccionaria o, menos 0.06 en su forma decimal.

Por lo tanto, un número negativo por un número positivo siempre es negativo sin importar si es fraccionario o decimal.

Regresando al acertijo, si “x” es un número positivo, ¿se cumple que un quinto de equis negativo por un número positivo sea positivo?

Como ya te habrás dado cuenta en casa, esto no se cumple cuando “x” es positivo. Porque un número negativo por otro positivo tiene como resultado un número negativo y éste obviamente no es mayor que cero.

Analiza ahora cuando “x” es igual a cero.

Finalmente observa qué sucede cuando “x” toma un valor numérico negativo.

Considera a “x” como 3.8 negativo o como comúnmente se le llama, menos 3.8, al sustituirlo en la expresión tienes que:

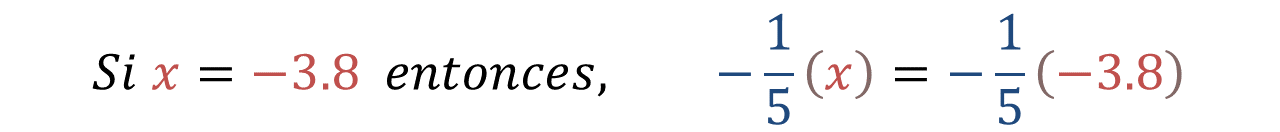
Para resolver la operación, puedes optar por convertir ambos factores a fracciones o, por otro lado, convertirlos a su forma decimal.

Primero resuelve el producto utilizando fracciones. Para ello, convierte a fracción el número (-3.8), esto es:

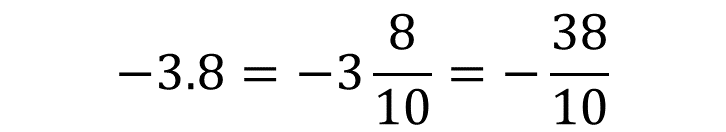
Ahora, sustituye y resuelve:

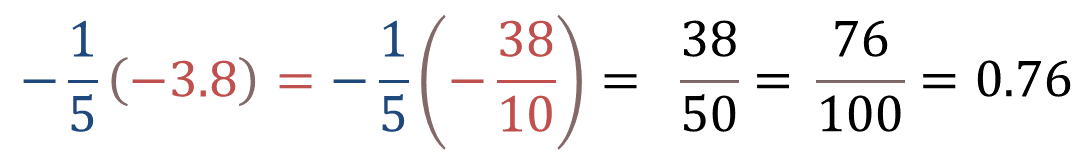
Entonces tienes que, un quinto negativo por 38 décimos negativo, da un número positivo porque negativo por negativo es positivo.

Finalmente, obtienes 38 cincuentavos es equivalente a 76 centésimos, entonces, el resultado es 0.76 positivo.

Una forma de comprobar que la operación es correcta es multiplicando los números en su forma decimal.

Por lo tanto, un quinto negativo es igual a 0.2 negativo, entonces multiplica a 0.2 negativo por 3.8 negativo.

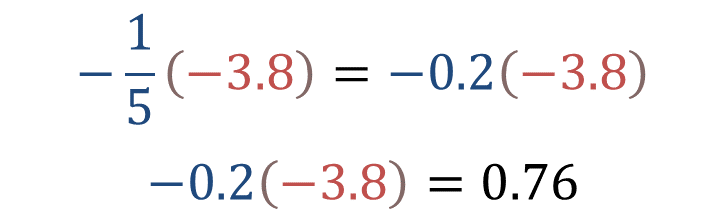
Como el producto de dos números negativos es positivo, el resultado es igual a 0.76 positivo.

Regresando al acertijo de, cuándo el producto de un quinto negativo por un número “x” es positivo, ya puedes responderlo, al comparar los casos que has analizado.

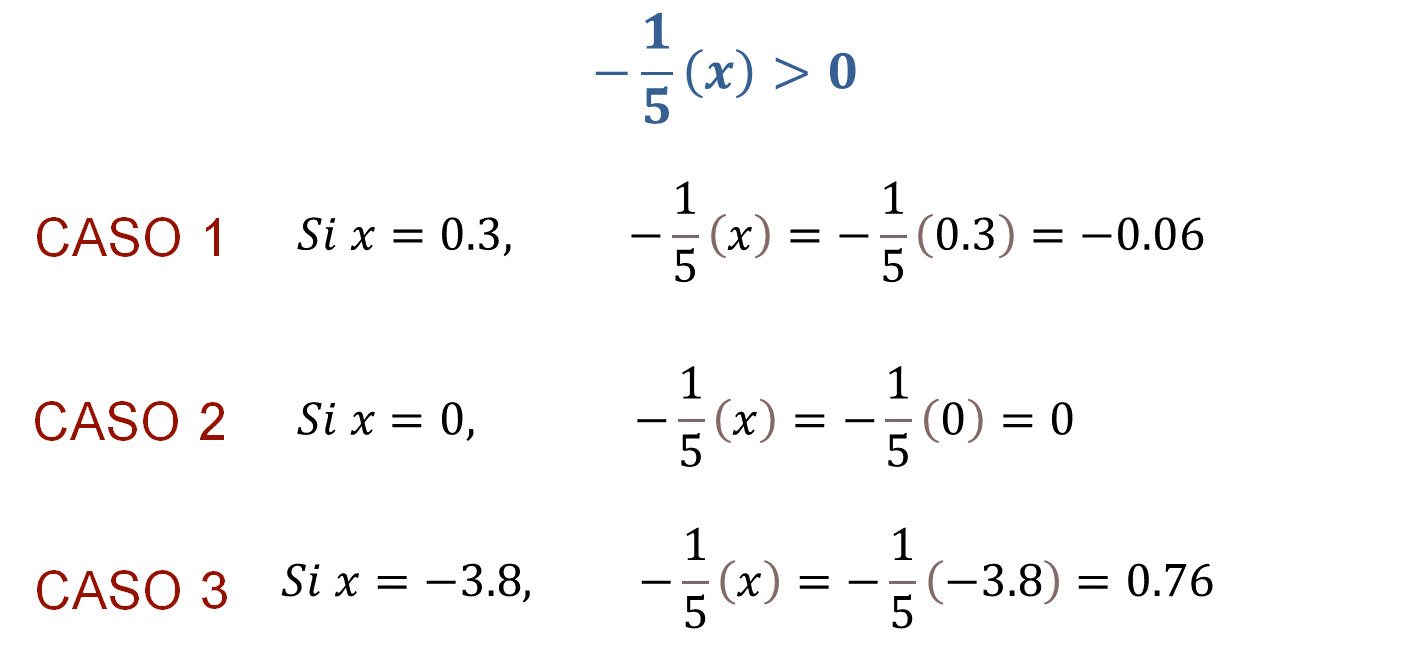
¿Con cuál de las tres opciones se resuelve el acertijo?

Con el tercer caso, es decir, cuando el número es negativo, ya que, al multiplicar un número negativo por otro negativo, el resultado es un número positivo.

Recapitulando, has analizado los diferentes casos en los que se realiza la multiplicación de números positivos y negativos, ya sea enteros, fraccionarios y decimales, y también has operado con el cero.

Asimismo, utilizaste la llamada regla de los signos para operar números positivos y negativos, que dice:

• El producto de dos números positivos es positivo y el producto de dos números negativos también es positivo.
• Por otro lado, el producto de un número positivo con otro negativo o viceversa, es negativo.

Con esto finalizas la sesión, dedicada a la multiplicación de números fraccionarios y decimales, positivos y negativos.

Recuerda que este es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de matemáticas segundo grado.

El reto de hoy:

Para aplicar lo aprendido, ahora te toca jugar con un par de dados virtuales. Cada dado tiene los números -3, -6, -2/3, 5/8, 0.5 y -2.5.

Multiplica correctamente los números que caerán.

Primer tiro:

Al tirar los dados cae el siguiente resultado:

¿Cuál es su producto?

Segundo tiro:

Se tiran los dados nuevamente y cae:

¿Cuál es el resultado?

Tercer tiro:

Se lanzan otra vez los dados y cae lo siguiente:

¿Cuál es la respuesta de este producto?

Cuarto tiro:

Se tiran los dados y cae:

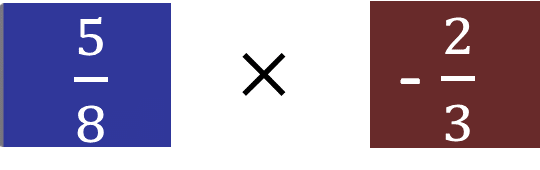
¿Cuál es su producto?

Quinto tiro:

Ahora, se lanzan por última vez los dados y cae:

¿Cuál es el resultado?

Realiza todas las operaciones que consideres necesarias para obtener el resultado correcto.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/