Múltiples representaciones algebraicas del perímetro

Múltiples representaciones algebraicas del perímetro

Aprendizaje esperado: formula expresiones de primer grado para representar propiedades (perímetros y áreas) de figuras geométricas y verifica su equivalencia en expresiones, tanto algebraica como geométricamente (análisis de las figuras).

Énfasis: formular conjeturas y validar las múltiples representaciones algebraicas del perímetro de las figuras y establecer su equivalencia.

¿Qué vamos a aprender?

Profundizarás en el estudio de las expresiones algebraicas equivalentes que modelan o representan propiedades de las figuras geométricas. En particular, determinarás la medida del perímetro de algunas figuras o superficies.

¿Qué hacemos?

Analiza y responde las siguientes preguntas:

1. ¿Qué es el perímetro de una figura?
2. ¿Cómo se calcula?
3. ¿Cómo se determina el perímetro de una figura geométrica?

En esta sesión, construirás argumentos para responder estas y muchas otras preguntas que seguramente te has planteado al estudiar temas de matemáticas.

Inicia ayudando a Brandon, alumno que estudia segundo de secundaria, a resolver la situación-problema que le asignó su profesor de Matemáticas.

La situación-problema dice así:

Situación-problema, centro deportivo.

Jesús trabaja en la construcción de un centro deportivo, y se están diseñando áreas para la práctica de diferentes deportes, como: frontón, futbol, basquetbol, salto de longitud, entre otros. Para delimitar las áreas y evitar accidentes se decidió colocar malla ciclónica en el perímetro de cada sección.

La malla ciclónica es una tela de alambre cuyo tejido tiene diversas formas geométricas, como rombos, cuadrados o rectángulos. Y se usa frecuentemente para delimitar áreas deportivas.

Jesús trazó las figuras que representan algunas secciones de las áreas deportivas, anotando el dato de los rollos necesarios para delimitar cada lado de las mismas. Analiza las figuras y responde algunas preguntas:

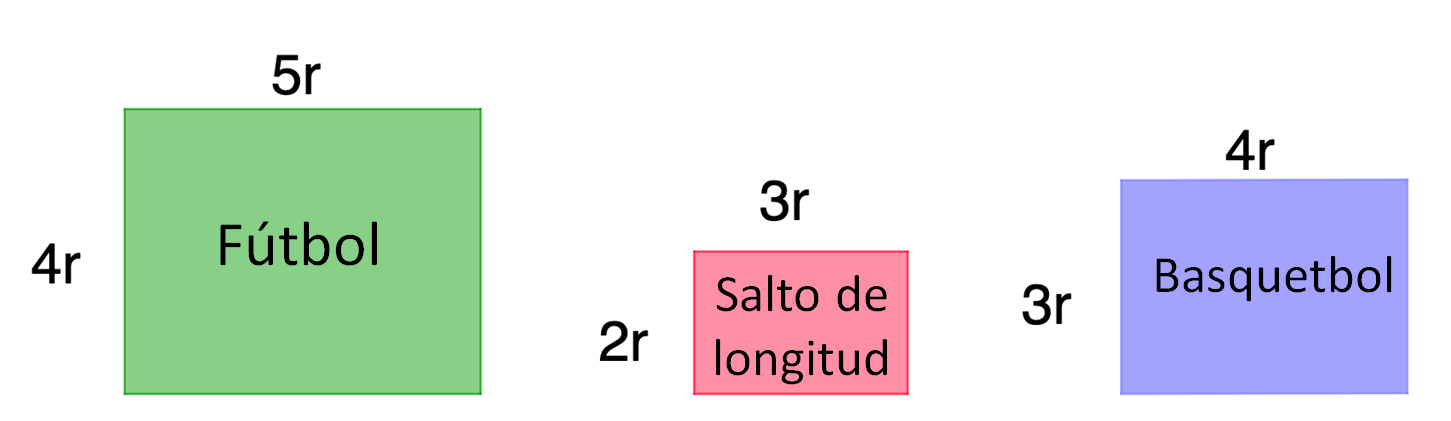
¿Qué sección ocupará mayor cantidad de malla ciclónica?

• Futbol
• Salto de longitud
• Basquetbol

Como puedes observar en la imagen, cada una de las secciones destinadas para practicar futbol, basquetbol y salto de longitud tiene una forma rectangular. En cada figura de las secciones deportivas se anotó el número de rollos de malla ciclónica para cada lado, donde la literal “r” representa un rollo completo de malla.

Si se va a colocar la malla:

¿Cuántos rollos de malla se requieren para delimitar el perímetro de cada sección?

¿Qué sección ocupará mayor cantidad de malla ciclónica?

Para responder la pregunta es necesario conocer cuál es la cantidad de malla ciclónica que se necesita para cada sección.

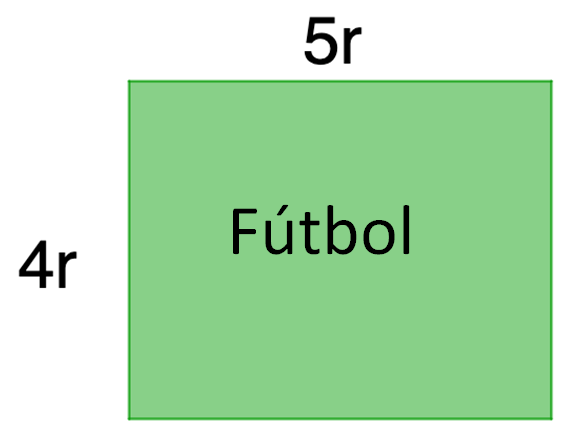
En la imagen, la primera figura rectangular representa la sección destinada como cancha de futbol, y se necesitan 4r de ancho y 5r de largo.

Cada “r” representa un rollo completo de malla ciclónica, entonces “4r” representa 4 rollos completos de malla ciclónica y “5r” representa 5 rollos completos de malla ciclónica.

¿Cuál es el perímetro de la sección destinada para practicar futbol?

A continuación, analiza las respuestas de Nataly y Fabián sobre el perímetro de la figura.

Nataly, una estudiante de secundaria dice que el perímetro de la sección para jugar futbol es:

P = 4r + 4r + 5r + 5r.

Fabián, su hermano, dice:

P = 2(5r) + 2(4r).

¿Qué razonamiento hay detrás de esas expresiones?

Continúa analizando el procedimiento que realizaron Nataly y Fabián para calcular el perímetro.

Nataly explicó que se basó en la idea de que el perímetro de cualquier figura se obtiene al sumar la medida de todos sus lados y, como en este caso es un rectángulo, entonces: a + a + b + b determinó que:

P = 4r + 4r + 5r + 5r.

Su razonamiento es correcto, además dijo, “puedo comprobar que estoy en lo correcto”. Por lo tanto, explicó que si se realizan las sumas de los sumandos que son iguales, se obtiene la expresión 8r + 10r = 18r, y si finalmente se realiza la suma, el resultado es 18r

Fabián explicó, que él sustituyó las medidas del rectángulo en la fórmula del perímetro de esta figura que es:

P = 2b + 2a

Por lo que, “tenemos dos veces la medida de la base, más dos veces la medida de la altura: P = 2(5r) + 2(4r) Él señaló que:

“Si se realizan las multiplicaciones, se obtiene: P = 10r + 8r, al resolver la suma, el perímetro es igual a 18r”

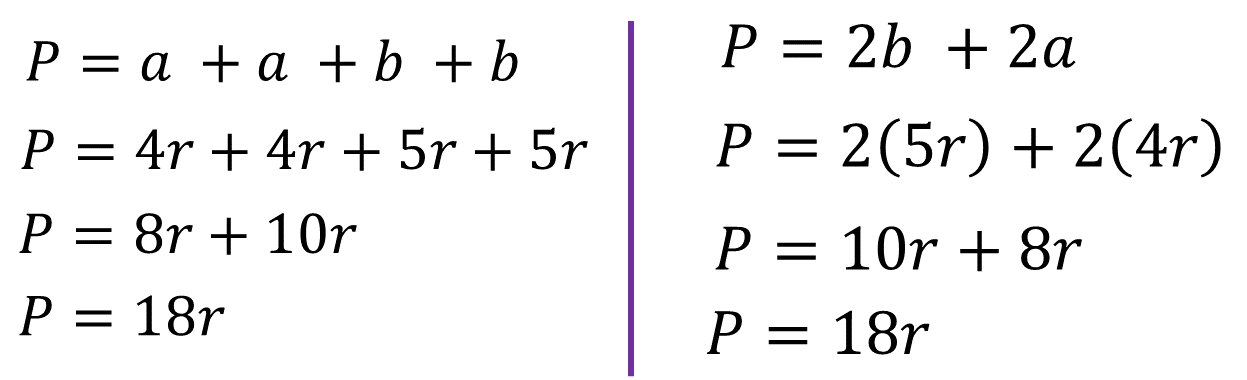
Tanto Nataly como Fabián propusieron expresiones algebraicas que modelan el perímetro de la figura rectangular que representa la sección destinada como cancha de fútbol; y comprobaron que sus expresiones son equivalentes, ya que llegaron al mismo resultado.

Es decir, si se escribe la expresión propuesta por Nataly y se iguala con la que propuso Fabián, se tiene:

4r + 4r + 5r + 5r = 2(5r) + 2(4r)

Si se realizan las operaciones indicadas en cada lado de la igualdad, en el lado izquierdo de la igualdad se suman los términos semejantes y en el lado derecho se multiplica 2 por 5r y se suma con el resultado de la multiplicación 2 por 4r. Ahora la igualdad queda como:

18r = 10r + 8r

Finalmente, se reducen los términos semejantes en el lado derecho de la igualdad, y queda: 18r = 18r

Lo anterior indica que las expresiones algebraicas propuestas por Nataly y Fabián para calcular el perímetro de la cancha de futbol son equivalentes.

De esta manera, se sabe que con las expresiones algebraicas equivalentes propuestas por Nataly y Fabián se puede expresar el perímetro con base en la cantidad de rollos de malla ciclónica que se necesitan para la sección de la cancha de futbol.

4r + 4r + 5r + 5r = 2(5r) + 2(4r)

Entonces, las dos expresiones algebraicas están escritas de manera distinta, pero tienen el mismo valor numérico después de asignar un valor a cada literal y realizar operaciones, son equivalentes.

Continúa con la sección que refiere al área de salto de longitud, bajo la explicación de Nataly y Fabián.

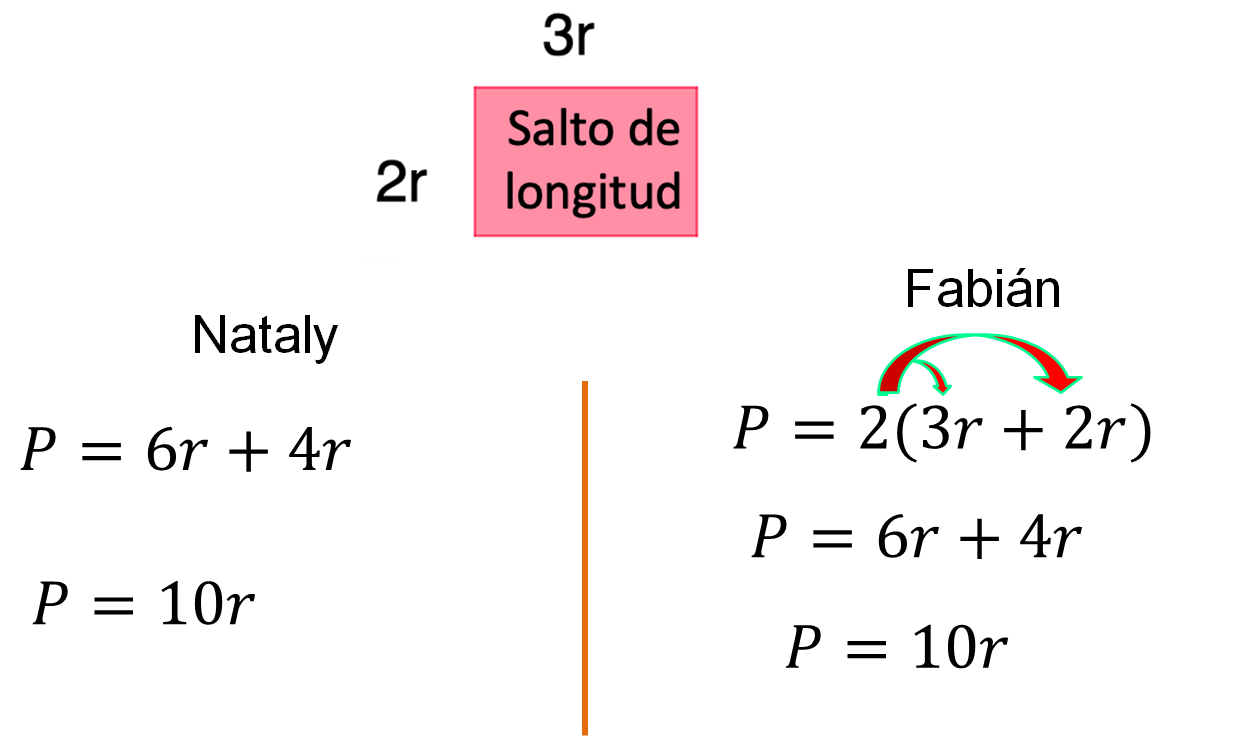
Al observar la sección destinada a la práctica del salto de longitud, se sabe que la medida de la base es 3r y la altura es 2r

Nataly establece la igualdad: P = 6r + 4r

Fabián escribe la igualdad: P = 2(3r + 2r)

Analiza las expresiones de Nataly y Fabián:

¿Estas expresiones pueden ser equivalentes?

¿Cómo puedes comprobar si hay o no una relación de equivalencia entre ellas?

Nataly dice:

“Para obtener el perímetro del rectángulo, consideré sumar dos veces la medida de la base, es decir 3r más 3r, más dos veces la medida de la altura, es decir, 2r más 2r, y obtuve la expresión: P = 6r + 4r”

Al resolver las operaciones para simplificar la expresión sumé 6r y 4r, y obtuve que el perímetro es igual a 10r”

Fabián explica:

“Decidí multiplicar por dos la suma de la medida de la base, que es 3r, más la medida de la altura, que es 2r”, por ello escribí la expresión: P = 2(3r + 2r), y sé que al efectuar la multiplicación su producto es P = 6r + 4r, ya que: 2 por 3r es igual a 6r, y 2 por 2r es igual a 4r

Al realizar la suma, 6r más 4r, el perímetro es igual a 10r”

Con la explicación de Nataly y Fabián:

¿Se comprueba que las expresiones son equivalentes? ¿Por qué?

Escribe tus respuestas y tus dudas.

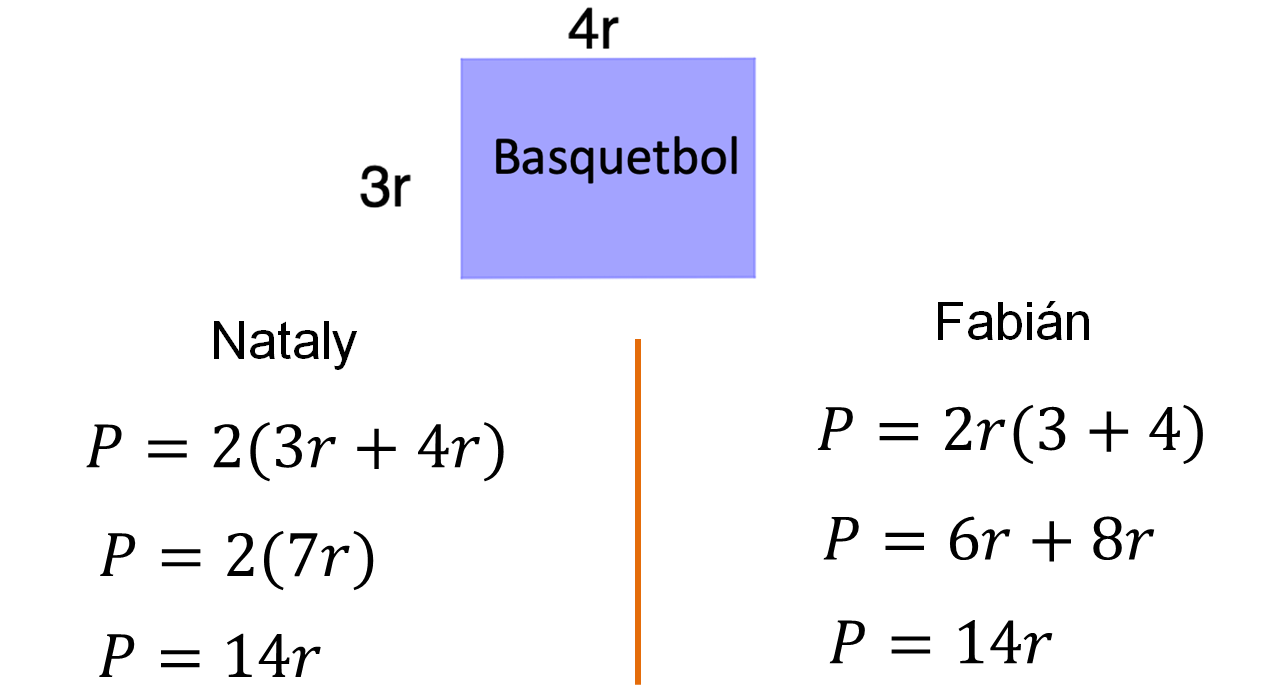
Ahora analiza lo que Nataly y Fabián realizaron para obtener el perímetro de la sección destinada al basquetbol.

Al observar la figura que representa la sección para jugar basquetbol en el centro deportivo, se identifica que se trata también de un rectángulo con medidas de “4r” de base y “3r” de alto.

Nataly escribió la siguiente expresión algebraica para calcular el perímetro:

P = 2(3r + 4r)

Por otra parte, Fabián escribió la siguiente expresión algebraica para calcular el perímetro:

P = 2r (3+4)

¿Consideras que estas dos expresiones algebraicas sean equivalentes?

Nataly explicó: “Igualé el perímetro con la multiplicación de dos por la suma de las medidas de la base que es 4r, y la altura 3r, obteniendo que P = 2 (7r). Al realizar la multiplicación obtengo la expresión algebraica para calcular el perímetro de la cancha de basquetbol, la cual es P = 14r”.

Fabián dijo que al observar la figura y el dato de las medidas del rectángulo identificó que ambas tienen la misma literal, por lo que igualó el perímetro con la suma de los productos dobles de cada longitud; es decir, P = 2r (3 + 4), al realizar las multiplicaciones se tiene la suma de los productos obtenidos, P = 6r + 8r. Finalmente, se reducen términos semejantes, obteniendo la expresión algebraica P = 14r

Para entender lo qué significan las expresiones equivalentes, sólo es cuestión de comprender sus representaciones y sus significados para poder establecerlas.

Ya resolviste el primer problema. Además, estudiaste una situación en la que calculaste el perímetro de las secciones que serán destinadas a la práctica de un deporte que es de utilidad. Por otro lado, entendiste las expresiones equivalentes.

Una forma de saber si dos expresiones son equivalentes consiste en utilizar las propiedades de reducción de términos semejantes y de agrupación.

Observa el siguiente ejemplo:

4xy + 2xz – 3xy + 5xz – yz = y (x – z) + 7xz

Si partes de la expresión algebraica de la izquierda, mediante la reducción de términos semejantes y las propiedades de agrupación, obtendrás la expresión de la derecha.

Para lograr lo anterior, se reducen términos semejantes:

Y luego por las propiedades de agrupación se tiene: “y”, que es factor común por x – z, + 7xz. Por lo tanto: 4xy + 2xz – 3xy + 5xz – yz, es una expresión equivalente de:

y (x – z) + 7xz

A continuación, revisa otra situación-problema.

Judith y Romina son compañeras de clase, su profesora de matemáticas les asignó una tarea y decidieron trabajar juntas para entregar una respuesta consensuada. Observa su tarea y la explicación de los procedimientos que utilizaron, con la finalidad de llegar a un acuerdo.

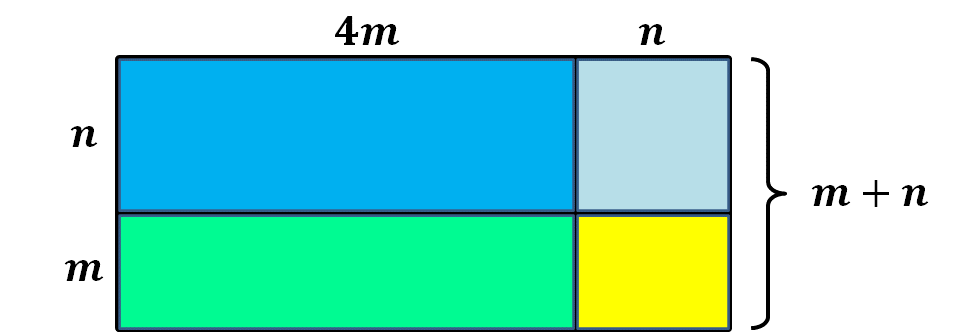
Situación-problema, modelo geométrico.

Se requiere obtener el perímetro de un modelo geométrico que es un rectángulo, el cual está compuesto por cuatro rectángulos identificados por colores.

El modelo geométrico mide de largo: 4m + n y de ancho: m + n

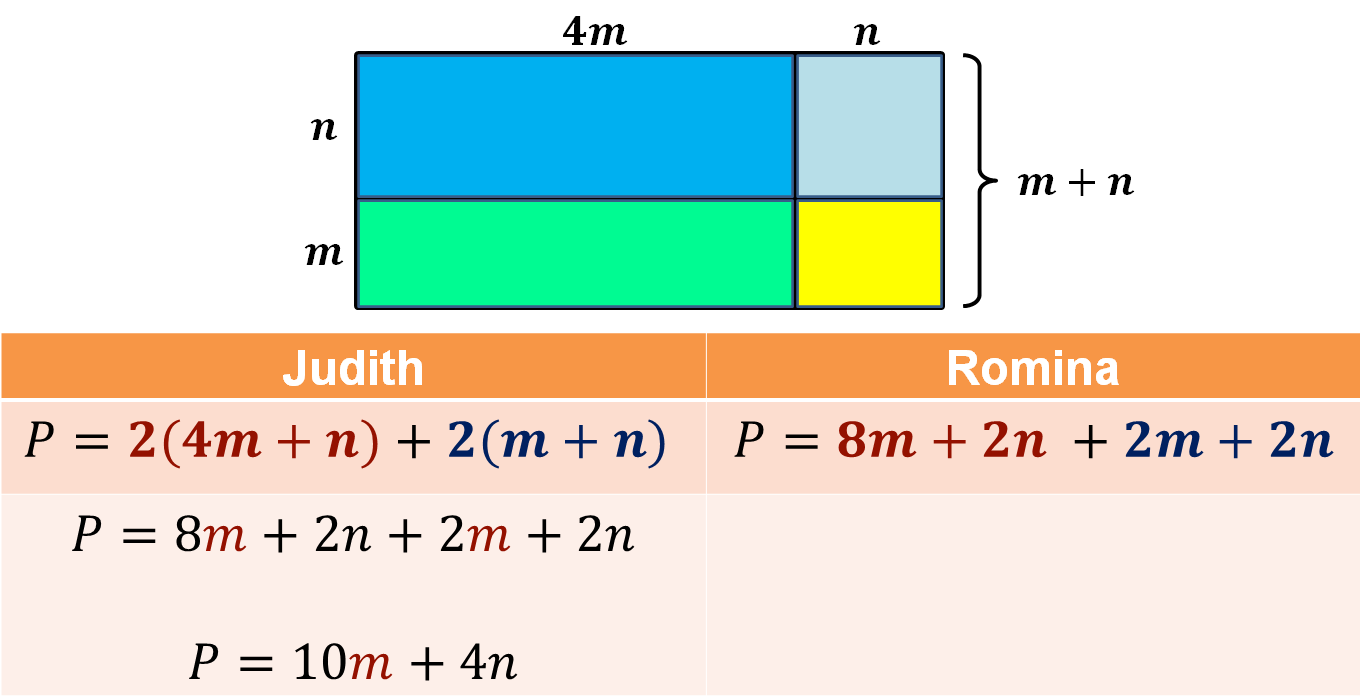
Judith modeló la expresión algebraica para el cálculo del perímetro de la siguiente manera:

P = 2(4m + n) + 2(m + n)

Mientras que Romina modeló la expresión para el cálculo del perímetro:

P = 8m + 2n + 2m + 2n

Si ambas se reducen términos semejantes, ¿sus resultados serán iguales? De ser así, ¿qué puedes concluir sobre cada una de las expresiones algebraicas que modelaron Judith y Romina?

Analiza los resultados:

Con ambas expresiones algebraicas se obtiene la misma medida, que en este caso es:

P = 10m + 4n

Se puede concluir que las expresiones algebraicas que modelaron Judith y Romina son equivalentes. Observa por qué:

Si se efectúa la suma de los términos semejantes, se obtiene 8m + 2m = 10m y 2n + 2n = 4n, entonces P = 10m + 4n, que es la expresión que utilizó Romina para determinar el perímetro del modelo geométrico.

En el caso de Judith, ella primero expresó el perímetro como la suma del producto de 2 por la medida de la base, que es 4m + n más el producto de 2 por la altura, que es m + n, quedando el perímetro como: P = 2(4m + n) + 2(m + n).

Después Judith sumó los términos semejantes: 8m + 2m = 10m y 2n + 2n = 4n

De esta manera, Judith obtuvo que P = 10m + 4n, que es la expresión que utilizó para determinar el perímetro del modelo geométrico.

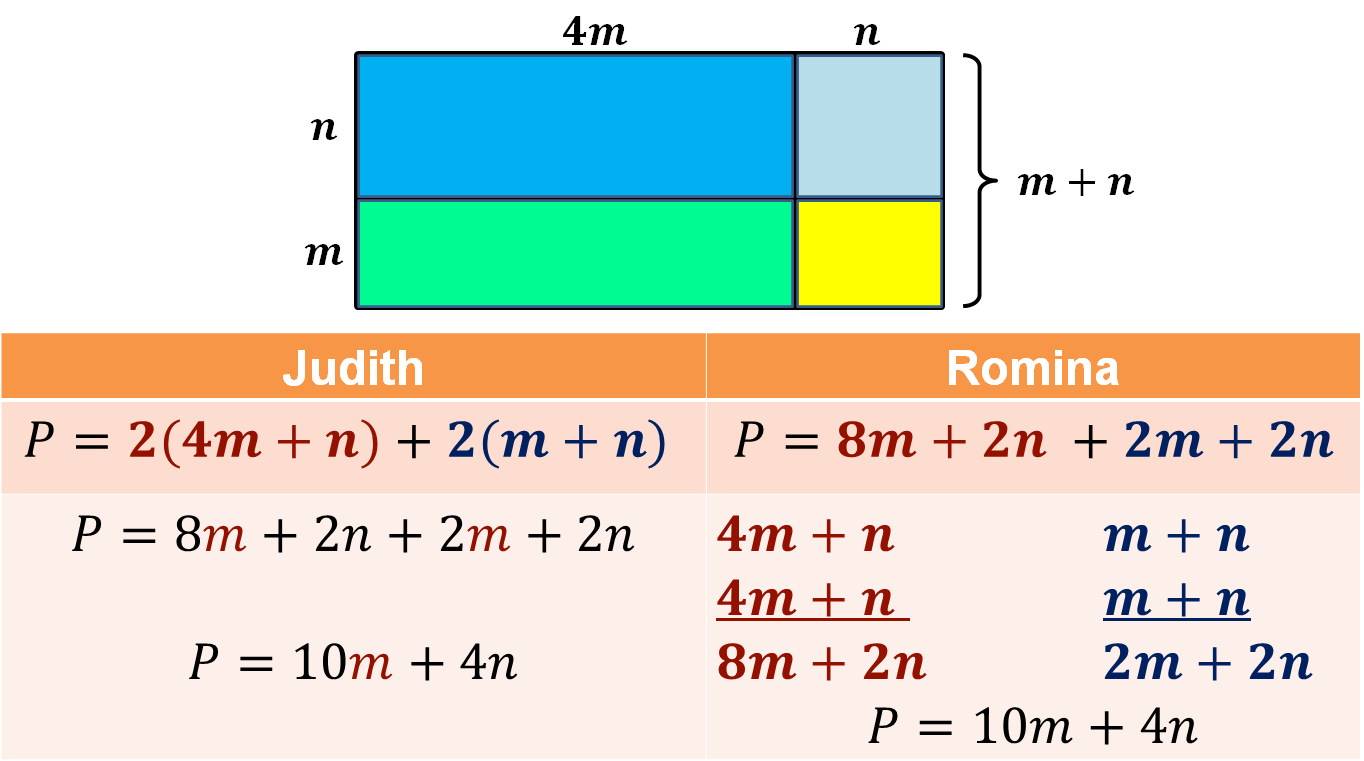
Para determinar el perímetro del modelo geométrico, Romina expresó el perímetro de manera aditiva:

P = 8m + 2n + 2m + 2n

Para establecer los sumandos de color rojo en la expresión algebraica de Romina, ella sumó dos veces la medida del largo:

4m + n

4m + n

y obtuvo 8m + 2n. Después sumó dos veces la medida del ancho:

m + n

m + n

y obtuvo 2m + 2n.

Ambas llegaron a un mismo resultado, y quedaron convencidas de la viabilidad de los procedimientos empleados.

Has analizado las expresiones algebraicas equivalentes y cómo verificar que sí lo sean.

Aplica lo aprendido al resolver la siguiente situación-problema. Analiza la información e intenta resolver el problema.

Situación-problema, cruz de cuadrados.

La figura está formada por cuadrados que miden “m” de lado.

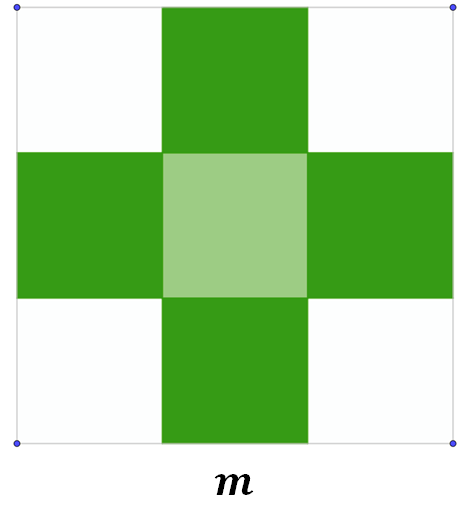
Escribe dos expresiones algebraicas equivalentes para calcular el perímetro de la cruz que se forma con los cuadrados verdes.

Verifica la equivalencia de las expresiones algebraicas propuestas asignando un valor numérico a la literal “m” y sustituyéndolo en cada expresión.

Con respecto a la indicación de escribir dos expresiones algebraicas equivalentes para calcular el perímetro de la cruz que se forma con los cuadrados verdes, Mariana, una alumna de segundo de secundaria, propone lo siguiente:

Se sabe que cada lado mide “m” y para determinar el perímetro de la cruz se escribe la medida de cada uno de sus lados, iniciando con el lado señalado con la flecha roja en el sentido de las manecillas del reloj hasta cerrar la cruz:

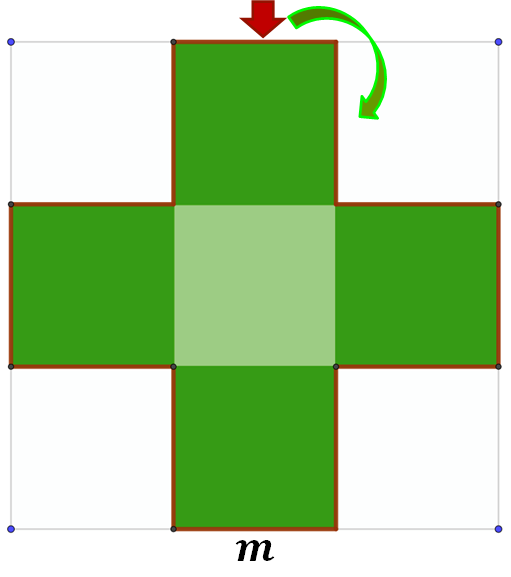
La expresión para determinar el perímetro de la cruz es:

P = m + m + m + m + m + m + m + m + m + m + m + m

P = 12m

Ahora, observa cómo Gerardo, otro alumno de secundaria, propone lo siguiente:

Como sólo tres lados de cuatro cuadrados forman el perímetro de la cruz, entonces el perímetro es 4 veces 3m, es decir:

P = 3m + 3m + 3m + 3m

Al resolver la suma se obtiene:

P = 12m

Revisa el razonamiento de Mariana y Gerardo. Ellos han propuesto escribir dos expresiones algebraicas equivalentes para calcular el perímetro de la cruz que se forma con los cuadrados verdes:

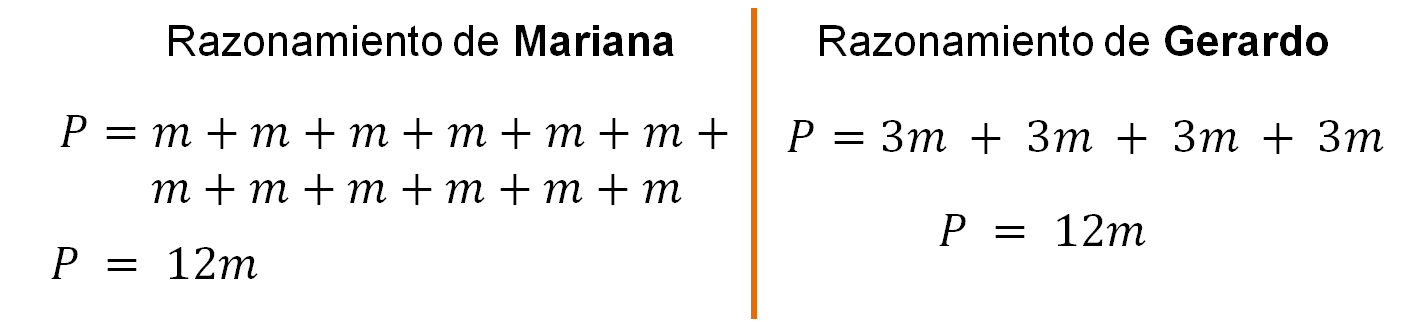
En la primera expresión, propuesta por Mariana: El perímetro es la suma de todos los lados “m”; por lo tanto, el perímetro es igual a “m” doce veces, y la suma total es 12m

En la segunda expresión, propuesta por Gerardo: el perímetro es 4 veces 3m, es decir, 3m + 3m + 3m + 3m = 12 m. Al resolver la suma se obtiene: P = 12m

Para verificar la equivalencia de las expresiones algebraicas propuestas, ellos han acordado asignar un valor numérico a la literal “m” y sustituirlo en cada expresión.

Mariana y Gerardo acordaron asignar a “m” el valor de 2 unidades, quedando de la siguiente manera:

En la primera expresión: El perímetro es la suma de todos los lados, por lo tanto, el perímetro es igual a 2 + 2 + 2 +… hasta tener el dos sumado doce veces. Entonces el perímetro es igual con 24 unidades.

En la segunda expresión: El perímetro es igual a 4 veces 3(2), es decir, 6 + 6 + 6 + 6. Al resolver la suma se obtiene: P = 24.

Se puede concluir que las expresiones algebraicas propuestas por Mariana y Gerardo para determinar el perímetro de la cruz son equivalentes, ya que ambas equivalen a 12m como perímetro igual.

Con el estudio de las situaciones-problema anteriores puedes conjeturar y validar representaciones algebraicas del perímetro de diversas figuras geométricas. Lograste comparar y verificar que, para representar el perímetro con expresiones algebraicas, existe la posibilidad de obtener varias opciones.

El perímetro es la suma de la medida de los lados de cualquier figura geométrica. Has determinado el perímetro de figuras cuyas medidas se asignan por una expresión algebraica, lo que produce expresiones algebraicas al representar sus perímetros.

Revisa otro ejemplo para que sintetices y fortalezcas lo que has revisado.

Un hexágono regular, cuya medida de sus lados es “a”

Se sabe que el perímetro, es la suma de los lados, por lo tanto, se calcula de la siguiente manera:

P = l + l + l + l + l + l

Se sustituye la medida del lado de la siguiente manera:

P = a + a + a + a + a + a

Se reducen términos semejantes:

P = 6a

Analiza la siguiente pregunta y elige el inciso correcto:

¿Cuál de las siguientes expresiones es equivalente a P = 6a?

1. P = a + 6
2. P = 3a + 3a
3. P = 6 + 6 + 6 + 6 + 6 + 6

En esta sesión, con ayuda de lo que aprendiste en tus grados escolares anteriores sobre el perímetro y el procedimiento para calcularlo, pudiste deducir el perímetro de figuras cuyas medidas están dadas por valores con literales, por lo tanto, al determinar perímetros obtuviste expresiones algebraicas. De igual manera, pudiste constatar que dos expresiones algebraicas pueden representar los mismos valores.

Recuerden que los materiales y recursos de esta sesión, son de apoyo, y que es importante que consultes otras fuentes para enriquecer lo que aquí aprendes.

El reto de hoy:

Resuelve la siguiente situación-problema:

La siguiente figura es un rectángulo que mide 4p de largo y 2p de ancho.

Se han registrado dos expresiones algebraicas con las que se calcula su perímetro.

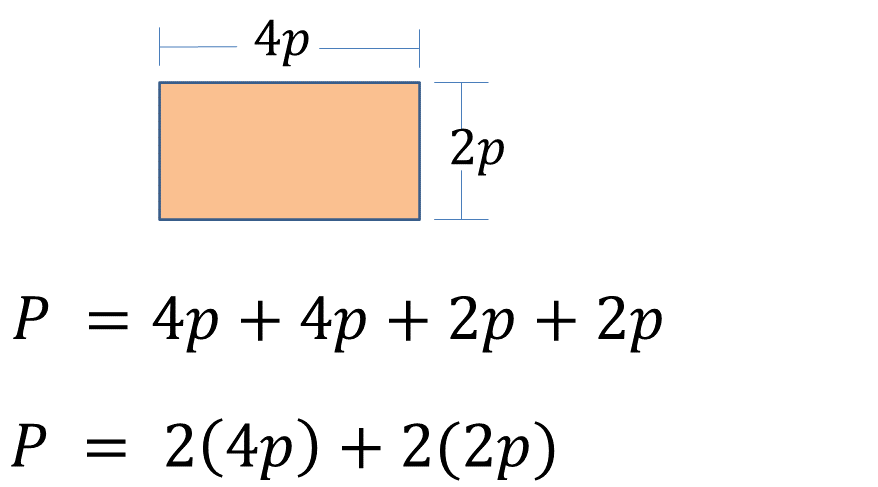
1. Plantea un problema empleando la figura, y
2. Explica con tus propias palabras por qué son, o no, equivalentes las expresiones algebraicas.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/