Métodos de resolución de ecuaciones cuadráticas
Métodos de resolución de ecuaciones cuadráticas
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: dar sentido y significado a los diferentes métodos de resolución de ecuaciones cuadráticas.
¿Qué vamos a aprender?
Durante esta sesión se describen los diferentes métodos de resolución de ecuaciones de segundo grado, también llamadas “ecuaciones cuadráticas”.
Las ecuaciones de segundo grado representan un tema extenso en Matemáticas. Por eso, se delimita el alcance del trabajo de esta sesión con el propósito de: “Dar sentido y significado a los diferentes métodos de resolución de ecuaciones cuadráticas”.
Como la factorización y la fórmula general. Toma en cuenta que el grado de una ecuación no depende del nivel escolar. El grado de una ecuación depende del exponente mayor de su incógnita.
Si el exponente mayor de la incógnita es 1, la ecuación es de primer grado. Aquellas cuyo exponente mayor es 2, son de segundo grado.
Las que tienen como mayor exponente el 3 son de tercer grado, y así sucesivamente.
Sin embargo, en la escuela secundaria, sólo se estudian las de primer y segundo grados.
Para el desarrollo de esta sesión, necesitarás tu cuaderno de notas, un lápiz y si cuentas con una calculadora úsala.
Se te recomienda registrar tus dudas, inquietudes y anotaciones respecto a cada uno de los temas.
¿Qué hacemos?
Comienza con la primera situación:

Para identificar la información del problema y determinar claramente lo que se pide obtener, debes de leer con atención el enunciado.
Primero identifica la incógnita y luego escribe la ecuación, después se elige el método de resolución para aplicarlo.

Es un cuadrado, sus lados son iguales.
La fórmula para calcular el área es, lado al cuadrado. Para esta situación “x” representa la medida del lado del cuadrado que se busca.
Al sustituir los valores en la fórmula del área, se tiene: “equis al cuadrado entre dos es igual a 98”. Ésta es la ecuación por resolver.
Y como la incógnita tiene exponente dos, es de segundo grado.
Continúa resolviendo, sólo hay un término que contiene a la incógnita, así que se puede despejar.
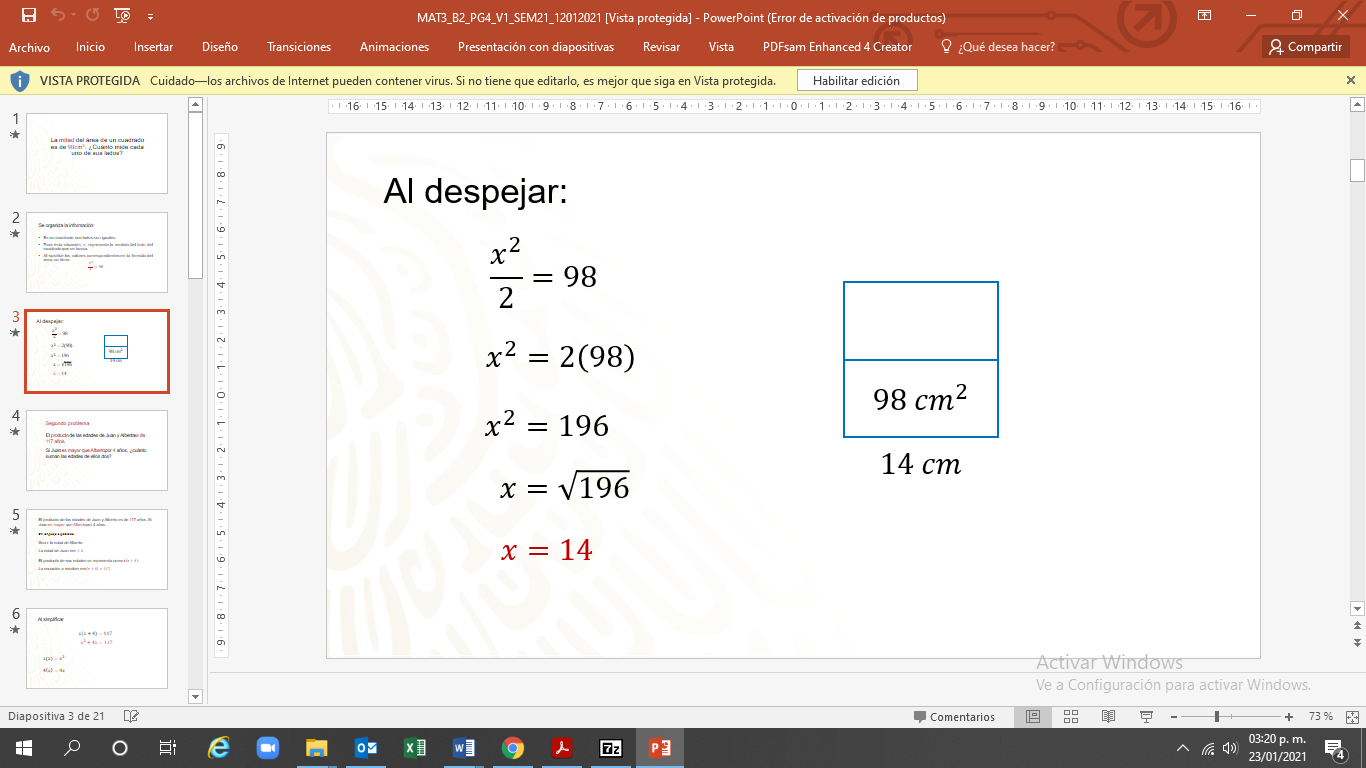
14 sí es el resultado
Sólo una observación. Al obtener la raíz cuadrada de 196, hay dos números cuyo cuadrado es 196. Son 14 y 14 negativo.
Entonces, hay dos soluciones para la ecuación. Cada ecuación tiene tantas soluciones o raíces como lo indica el grado al que pertenece.
Una ecuación de primer grado tiene una solución. La ecuación de segundo grado tiene dos soluciones o raíces. Las de tercer grado tienen tres raíces y así, sucesivamente.
Y, aunque las dos soluciones satisfacen la ecuación, por tratarse de un problema geométrico, se toma la solución positiva.
Cada lado del cuadrado mide 14 cm.
Como puedes ver, la resolución de ecuaciones cuadráticas puede simplificarse al elegir las herramientas matemáticas más convenientes.
Analiza la situación 2:
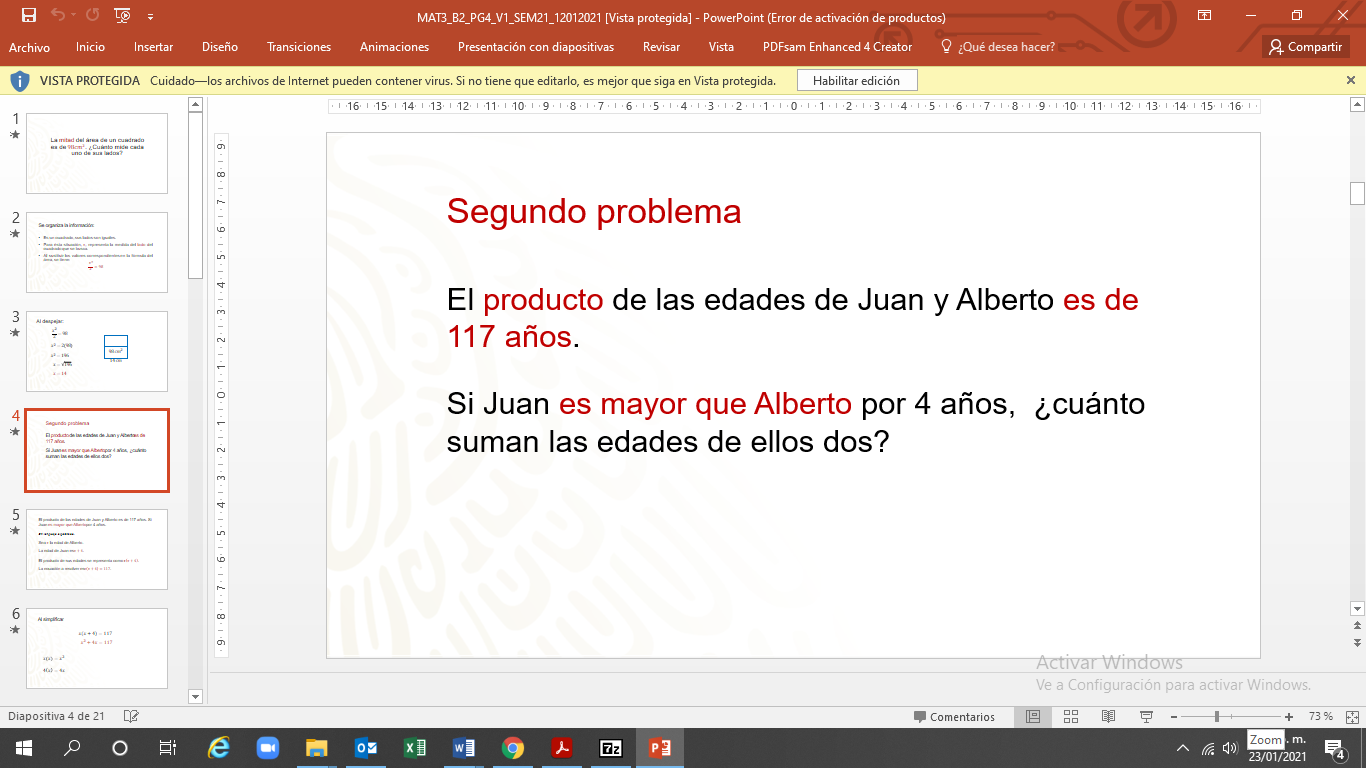
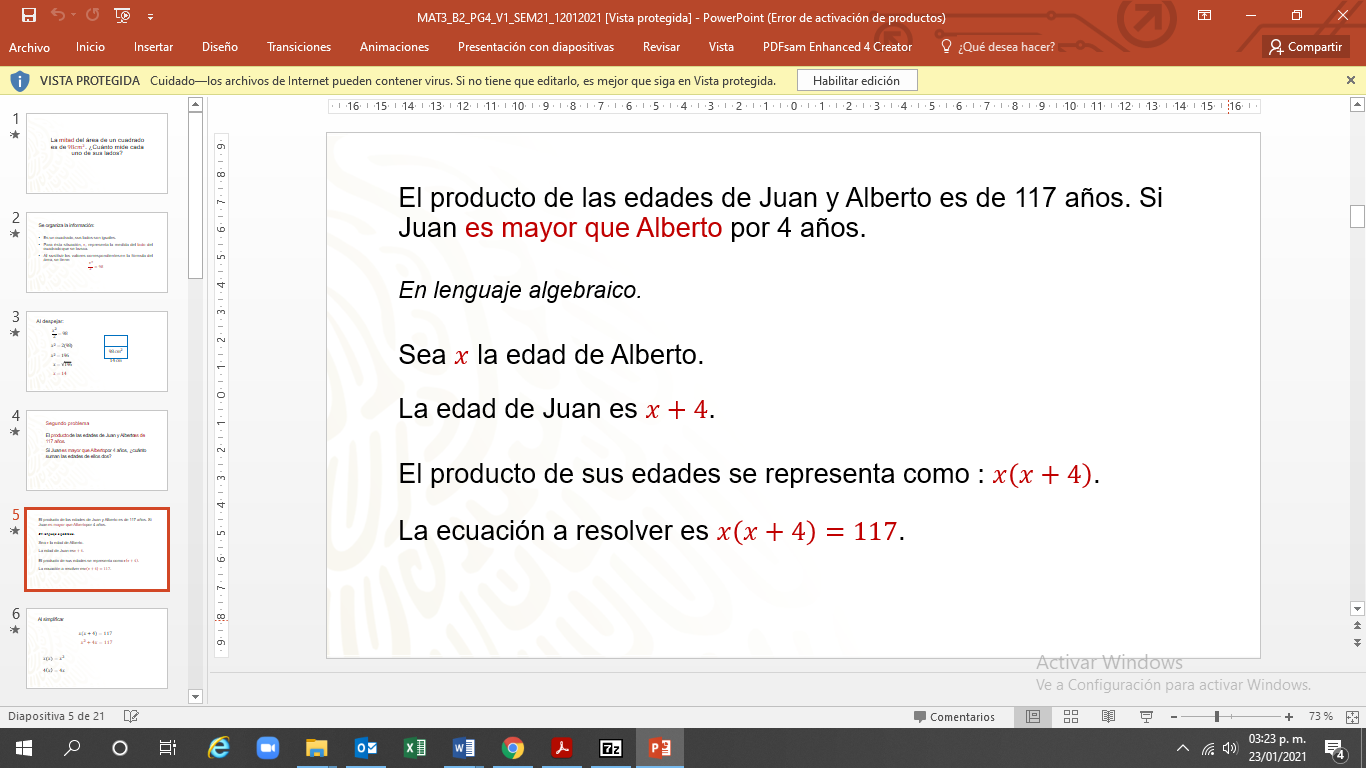
Así, cuando se conozca la edad de Alberto, sólo se debe de sumar 4 años para saber la edad de Juan.
El producto de sus edades se representa como “x(x+4)”. La ecuación para resolver es: “x” por “x” más cuatro igual a 117
En esta ocasión no se puede despejar, pero para estar seguros, se simplifica y se escribe en la fórmula general.
Para simplificar, se multiplica “x” por “x” igual a “x” al cuadrado. 4 por “x” es igual a 4x. La ecuación es “x” al cuadrado más 4 “x” igual a 117
La fórmula general se escribe:
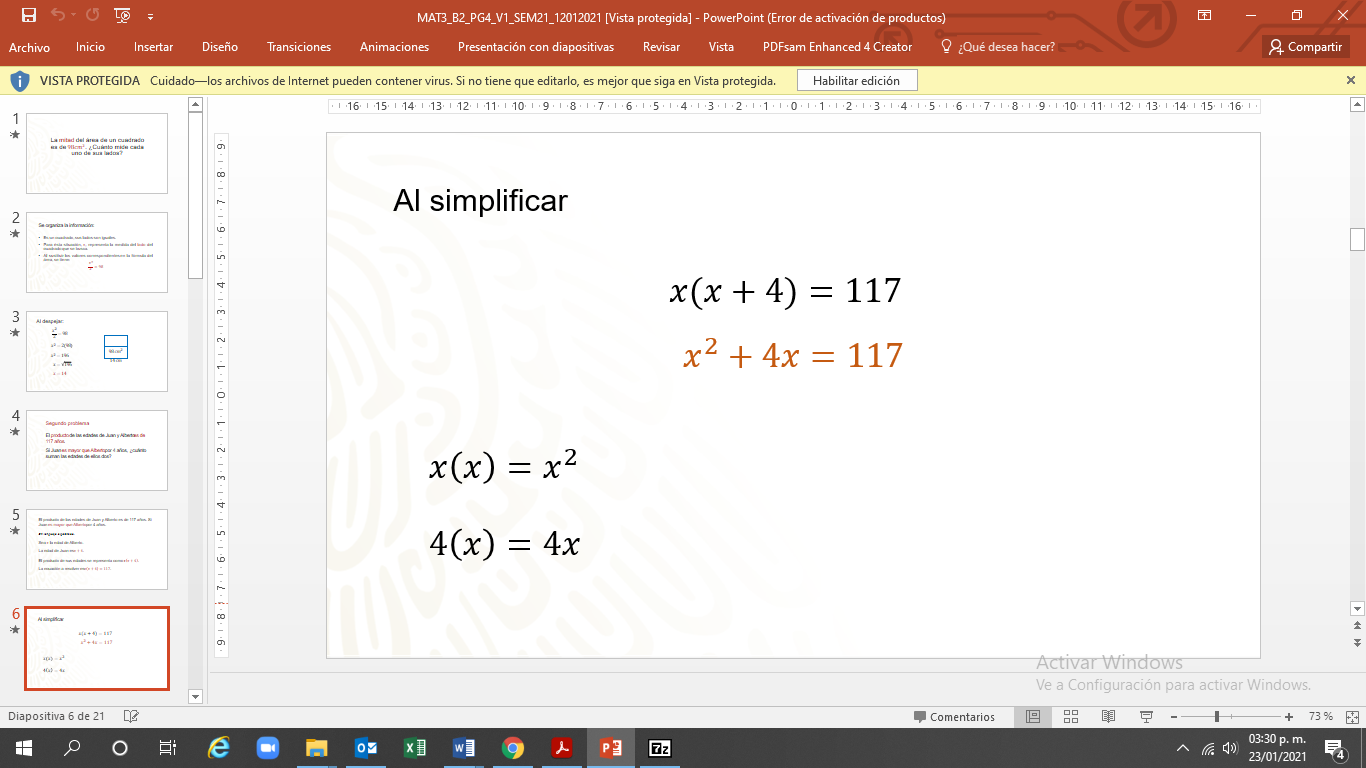
Para describir cuál es la fórmula general de la ecuación de segundo grado, observa el siguiente video:
- Video 1_PG4_S21
(del minuto 07:07 al minuto 08:23)
https://youtu.be/IyOxEvZNKaw
Ya simplificada, se escribe en la fórmula general: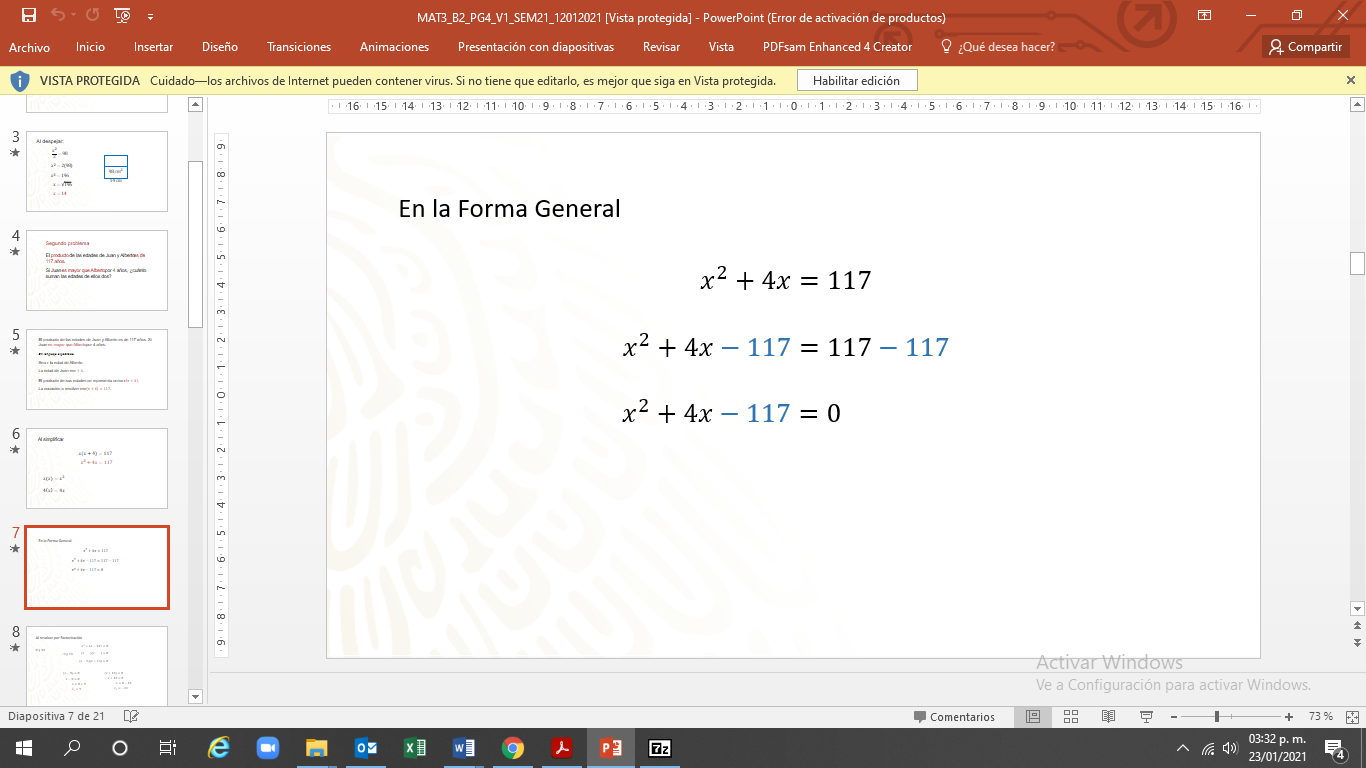
Se resta 117 en ambos lados de la igualdad. Y la ecuación es “x” cuadrada más 4”x” menos 117 igual a cero.
Y como no se puede resolver por despeje, antes de usar la fórmula general, conviene evaluar si es posible resolver por factorización.
Es un trinomio de segundo grado, se podría factorizar como el producto de binomios con término común.
En cada binomio, el término común es “x”.
Los términos no comunes que completan los binomios son dos números que sumados den 4 y multiplicados den 117 negativo.
¿qué números crees que cumplen con esa condición?
En situaciones como ésta, debes de usar toda la habilidad de la que dispones para ayudarte.
¿A qué número, múltiplo de 10, se aproxima 117?
Es cercano a 120
Si multiplicas 10 por 12 es 120
10 y 12 no son los números que estás buscando, pero deben de estar cerca.
Y once por once son 121
No olvides que uno es 4 unidades mayor que el otro.
Entonces son 9 y 13
Escribe en los binomios con término común para terminar la solución a este problema.
Los números son 9 y 13, se identifica con qué signo los términos “no comunes” a los binomios cumplen con la condición dada.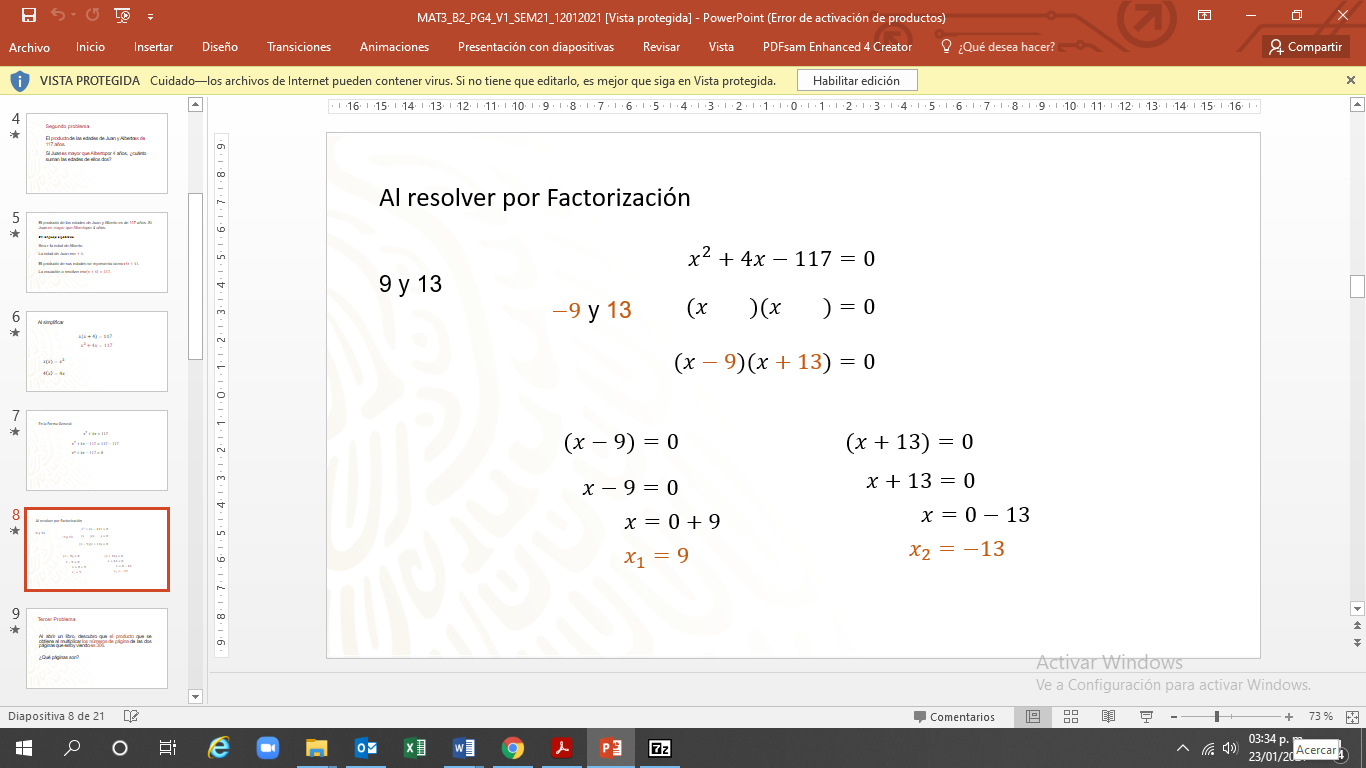
9 negativo y 13 positivo son los términos no comunes.
Los binomios son “x” menos 9” y “x” más 13”
Cada binomio se iguala a cero, para obtener la solución a estas dos ecuaciones de primer grado.
Las raíces de las ecuaciones son “x” igual a 9 y “x” igual a 13 negativo.
9 y 13 negativo son las raíces de la ecuación, pero para el problema, las edades de Juan y Alberto no pueden ser años negativos.
Entonces únicamente se considera la raíz positiva. De acuerdo con lo planteado al inicio, “x” representa la edad de Alberto, es decir, 9 años.
Juan, que es 4 años mayor, tiene 13 años. Pero aún no terminas, lo que se pide en el problema es la suma de sus edades, la cual es igual a 22
Es importante responder todas las preguntas del problema.
Resuelve la situación 3.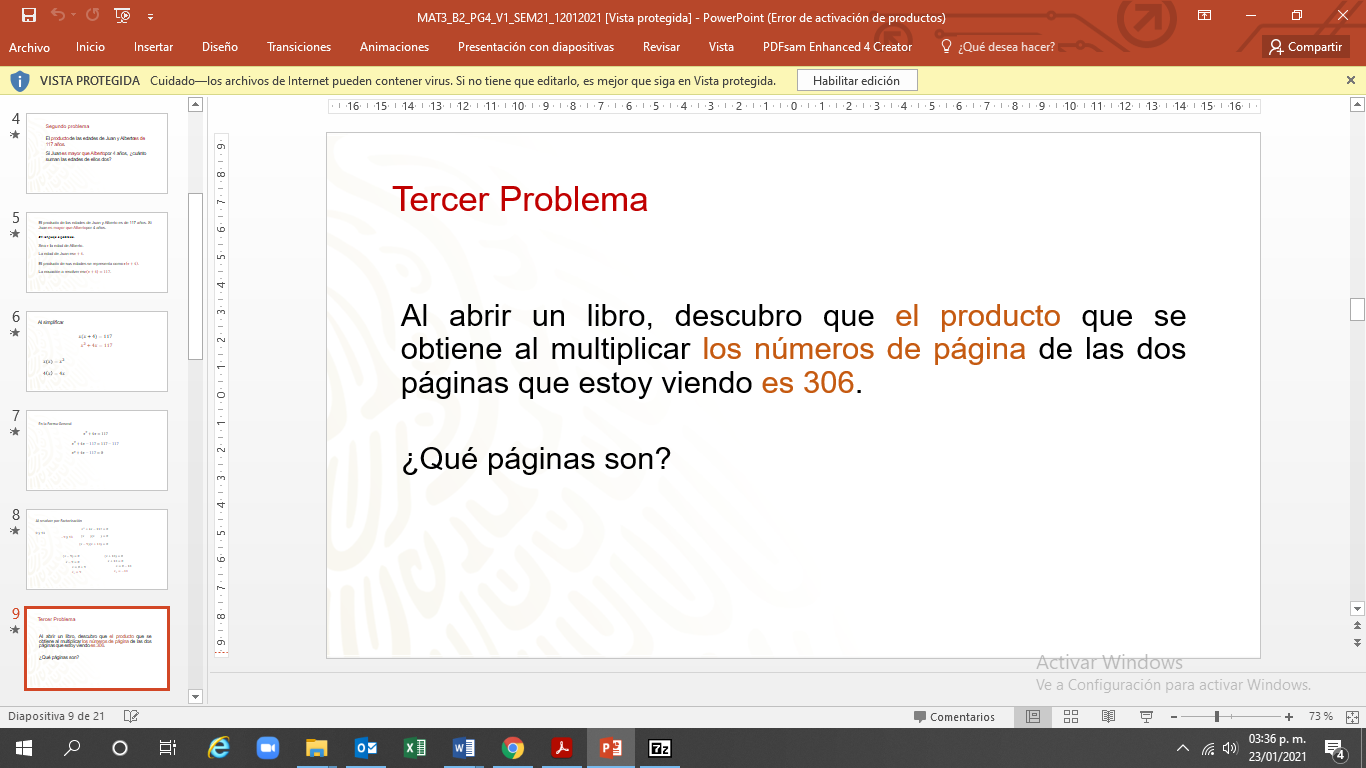
El problema se refiere a un libro abierto y las páginas que quedan a la vista. Estas páginas tienen numeración consecutiva, ¿cómo se representan números consecutivos de manera algebraica?
Aunque el problema no lo menciona abiertamente, tu experiencia sugiere que son números consecutivos.
Mucho del éxito al resolver problemas depende del planteamiento correcto de la ecuación o expresión algebraica.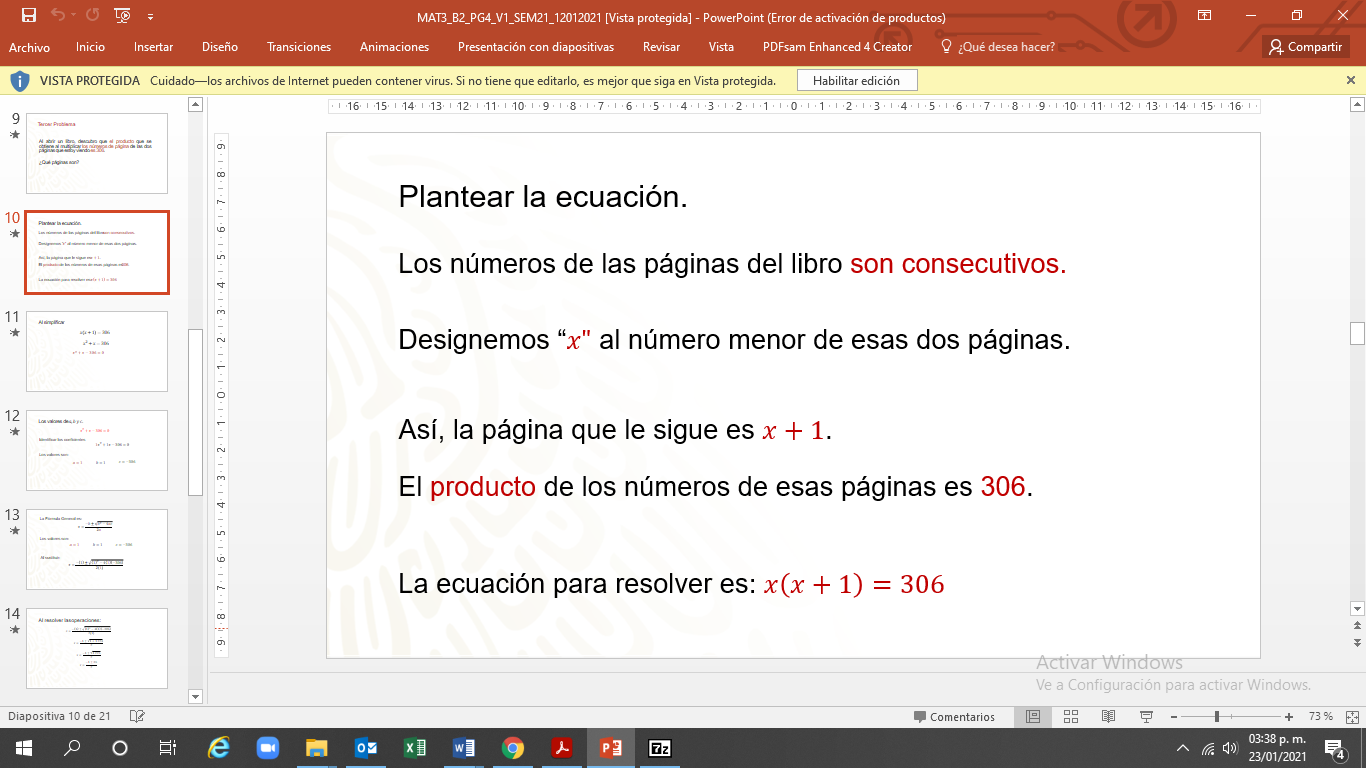
Y, de nueva cuenta, se simplifica y pone en la fórmula general.
La ecuación es “x” por “x” más 1 igual a 306”.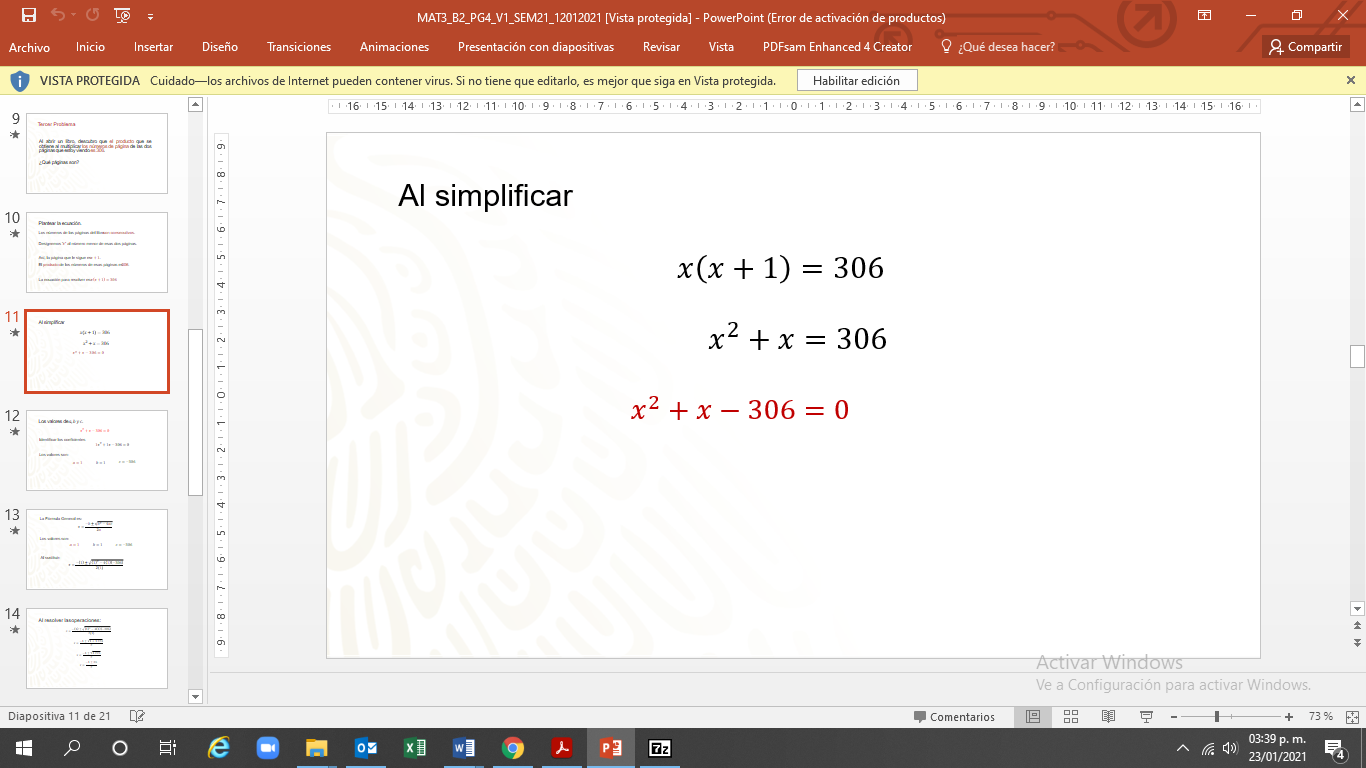
Esta ecuación no se resuelve despejando. Si se considera resolver por factorización, se buscarían dos números que multiplicados den 306
Ensayar las posibles combinaciones puede llevar más tiempo que resolver por fórmula general. ¿Recuerdas la fórmula general?
Es “equis es igual a “b” negativa, más menos, raíz cuadrada de “b” cuadrada menos 4ac. Todo sobre “2a”
Los valores de “a”, “b” y “c” de la fórmula general, se obtienen de los términos de la ecuación en su fórmula general. Observa el siguiente video. - Video 2_PG4_S21
(del minuto 13:48 al minuto 14:55)
Con esa información se resuelve la ecuación usando la fórmula general.
Observa el procedimiento.
La ecuación, en la fórmula general es “equis al cuadrado, más equis menos 306 igual a cero”.
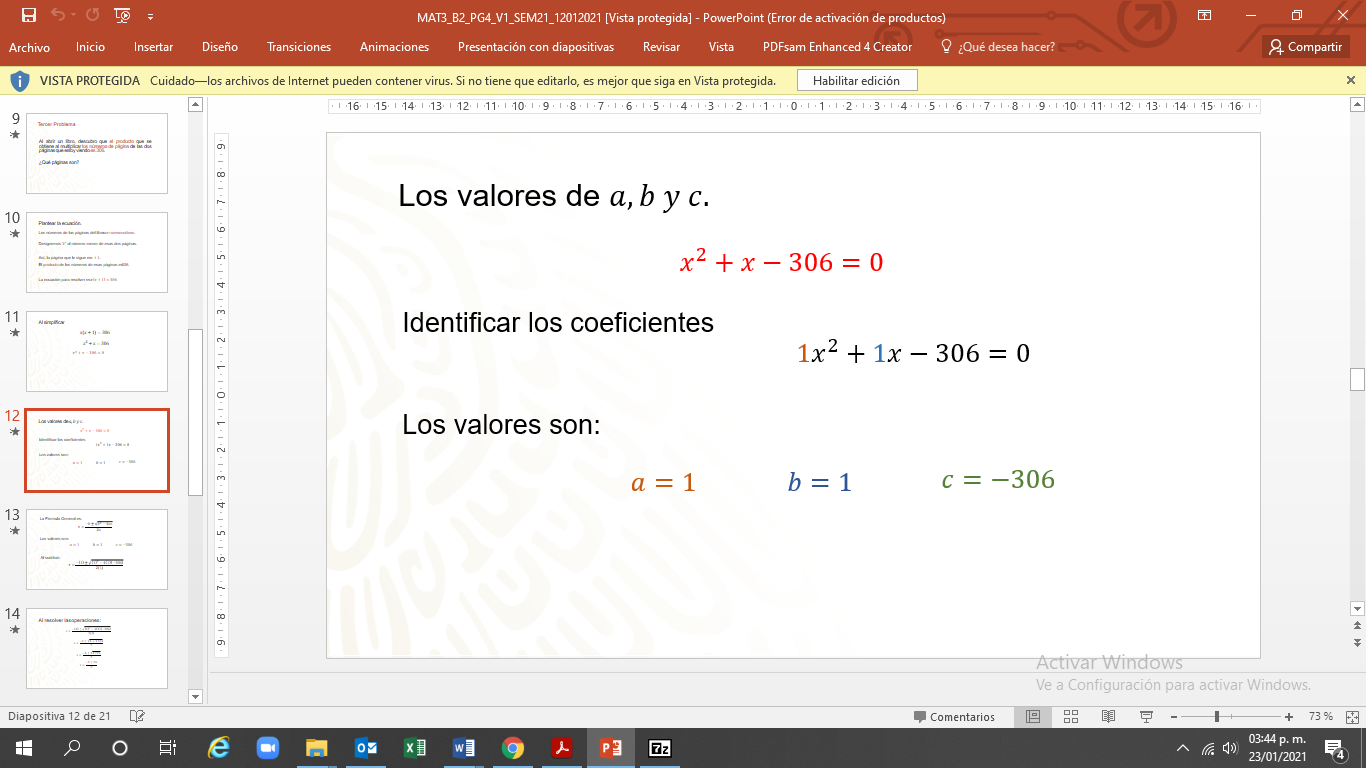
Aunque no se muestran de manera explícita, el coeficiente de “x” cuadrada y de “x” es 1”
El término constante es 306 negativo.
El valor de “a” es 1. El valor de “b” es también 1 y, el valor de “c” es 306 negativo.
Se sustituyen esos valores en la fórmula general para determinar las raíces de la ecuación.
Es importante escribir la fórmula, aunque te la sepas de memoria.
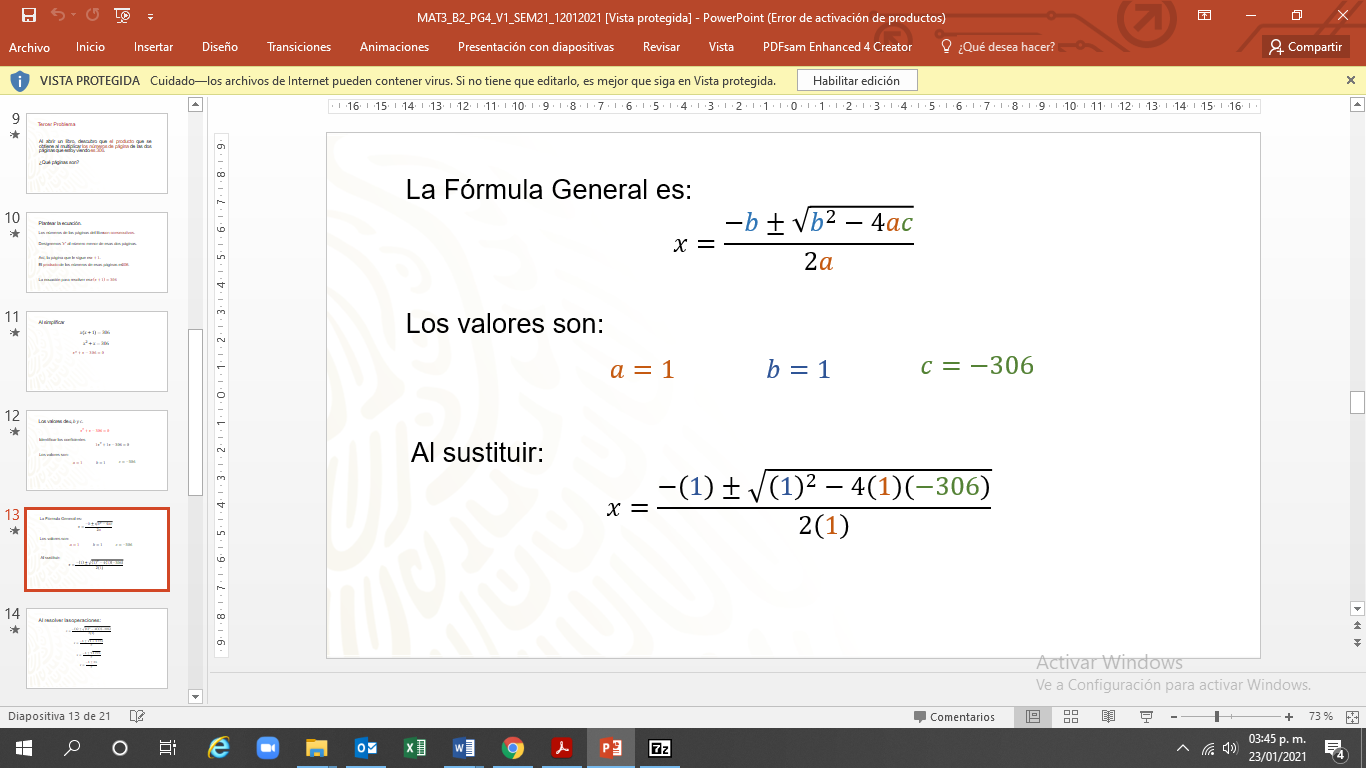
Se sustituyen los valores de “a”, “b” y “c”, utilizando paréntesis para conservar las operaciones indicadas en la fórmula.
Al resolver las operaciones:
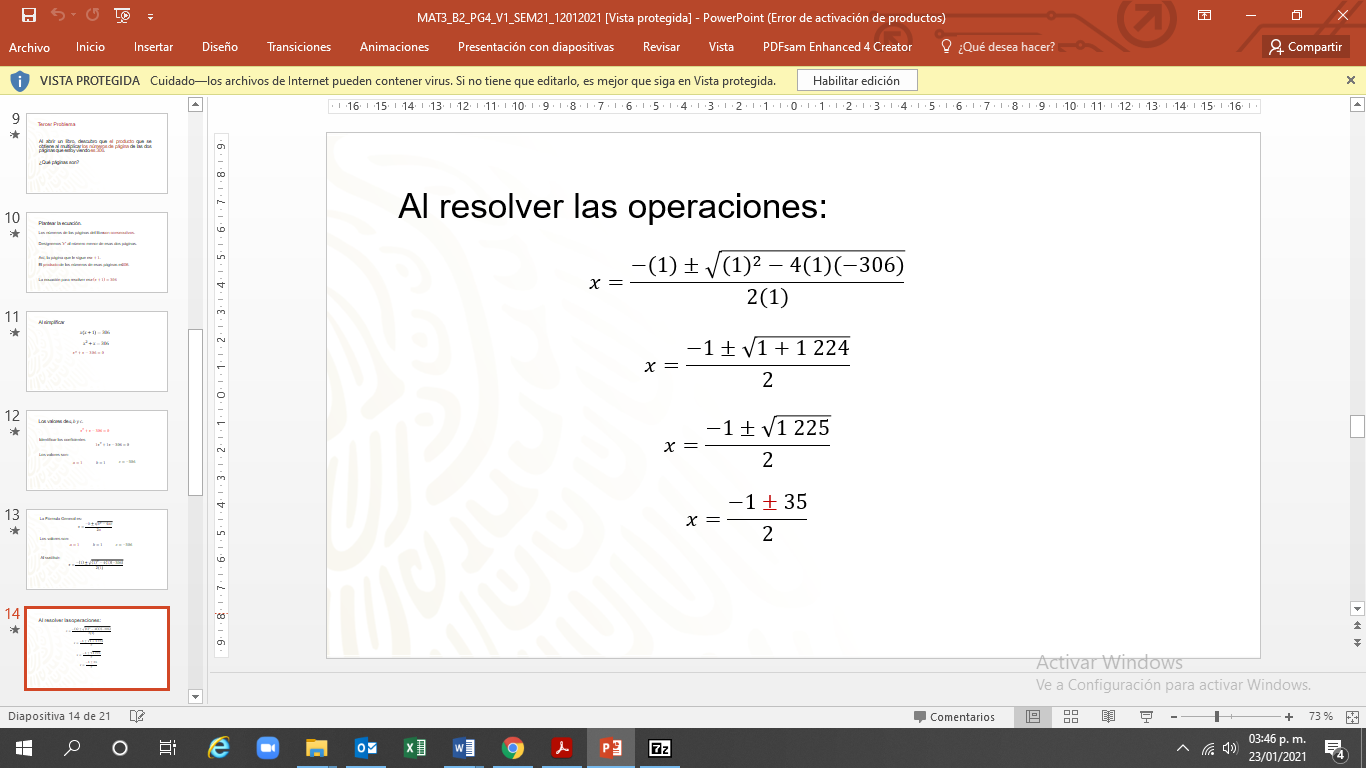
“x” es igual a uno negativo, más menos, raíz cuadrada de uno al cuadrado, que es uno. El producto de 4 negativo, por uno y por 306 negativo es 1 224 positivo. En el denominador, dos por uno es dos.
“x” es igual a uno negativo, más menos, la raíz cuadrada de 1 225. El denominador es dos.
“x” es igual a uno negativo más menos 35. Entre dos.
Se deben de considerar las dos alternativas del signo más menos.
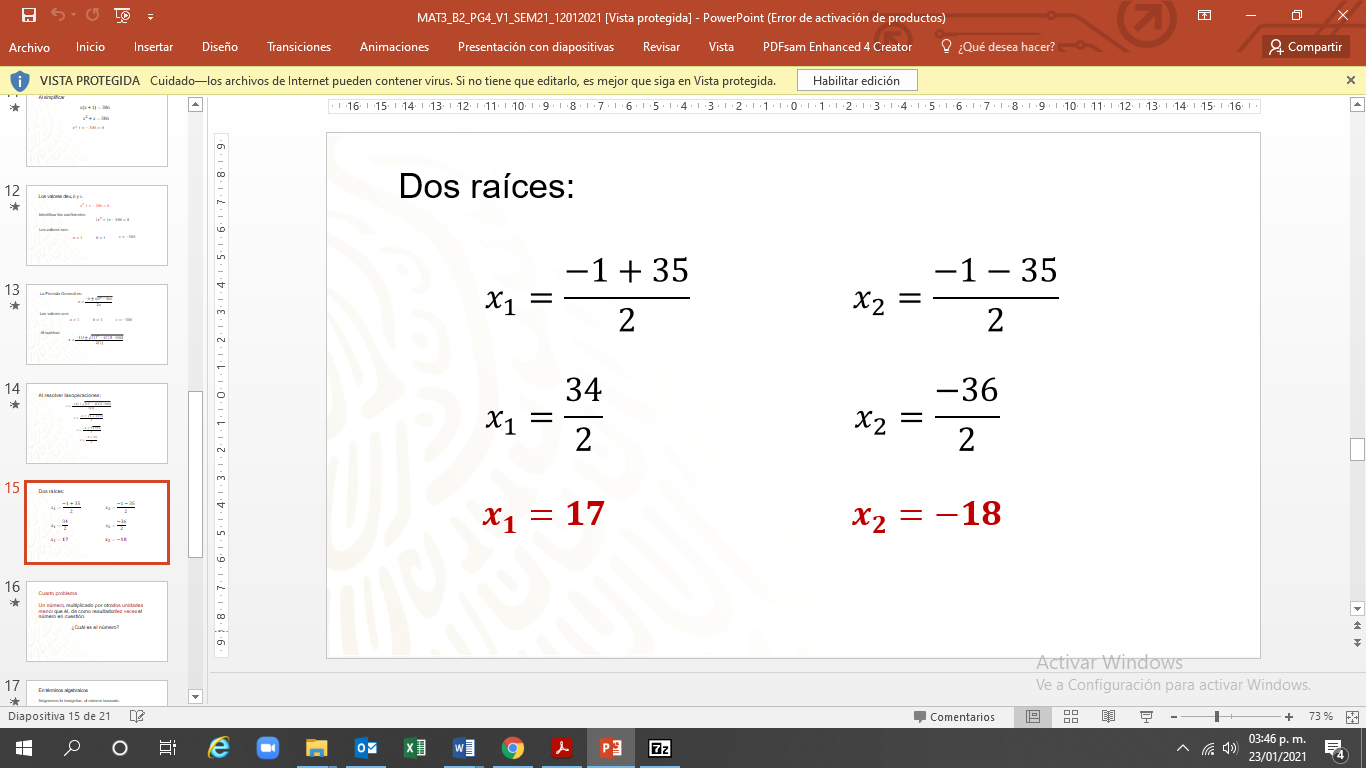
La primera es la opción que suma el resultado del radical: “x1” es igual a uno negativo más 35, todo entre dos.
“x1” es igual a 34 entre dos.
“x1” es igual a 17
Para “x2”, se considera la opción que resta el resultado del radical:
“x” dos es igual a uno negativo menos 35, todo entre dos.
“x” dos es igual a 36 negativo entre dos.
“x” dos es igual a 18 negativo.
Como las páginas de los libros son números positivos, se elige “x” igual a 17
Ahora, “x” representa a la página de número menor, la página consecutiva es 17 más 1.
Es decir 18
Las páginas del libro abierto son la 17 y la 18
Con la fórmula general, se puede resolver cualquier ecuación de cuadrática.
Aunque, como has podido notar, resulta laboriosa e incluye varias operaciones aritméticas.
Por eso, conviene valorar las características de la ecuación para elegir el método más conveniente.
Observa la situación 4:
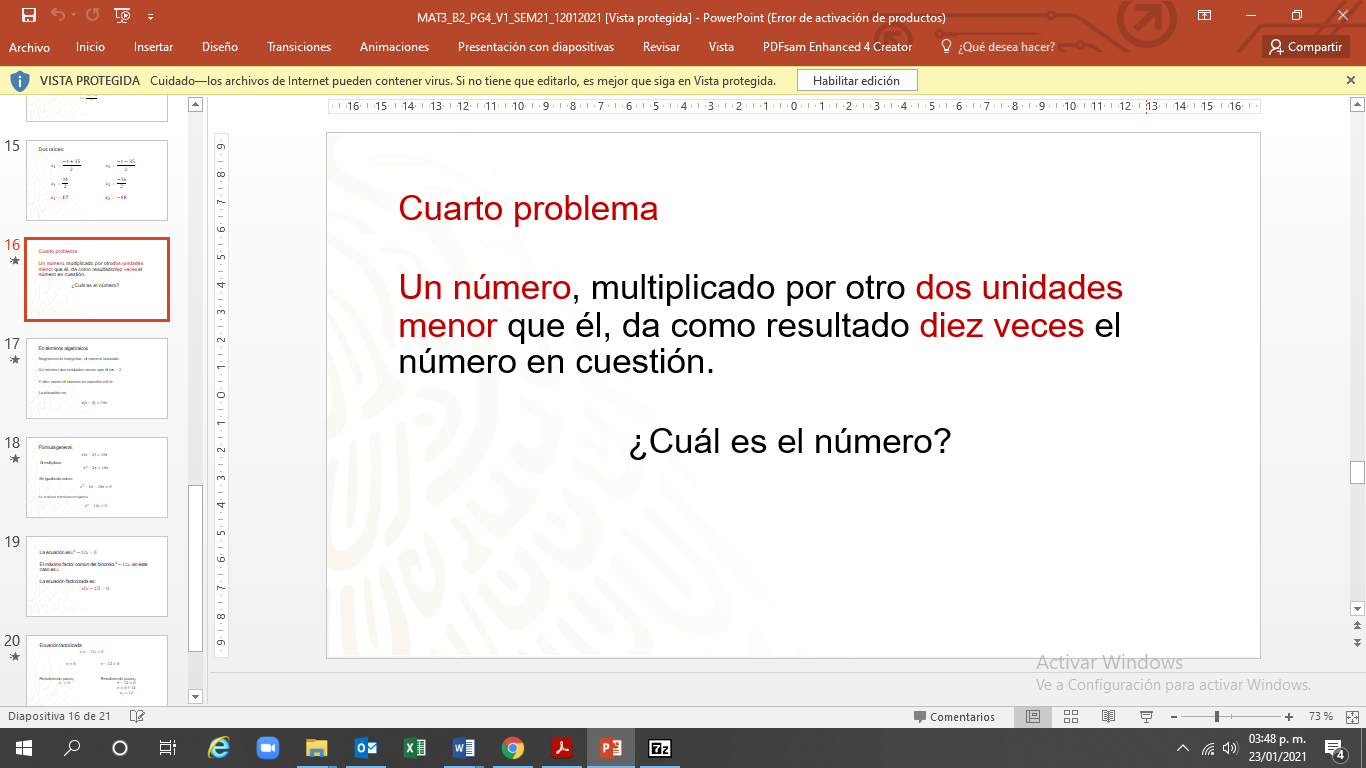
Plantear correctamente la ecuación con la información del ejercicio permite tener la solución adecuada.
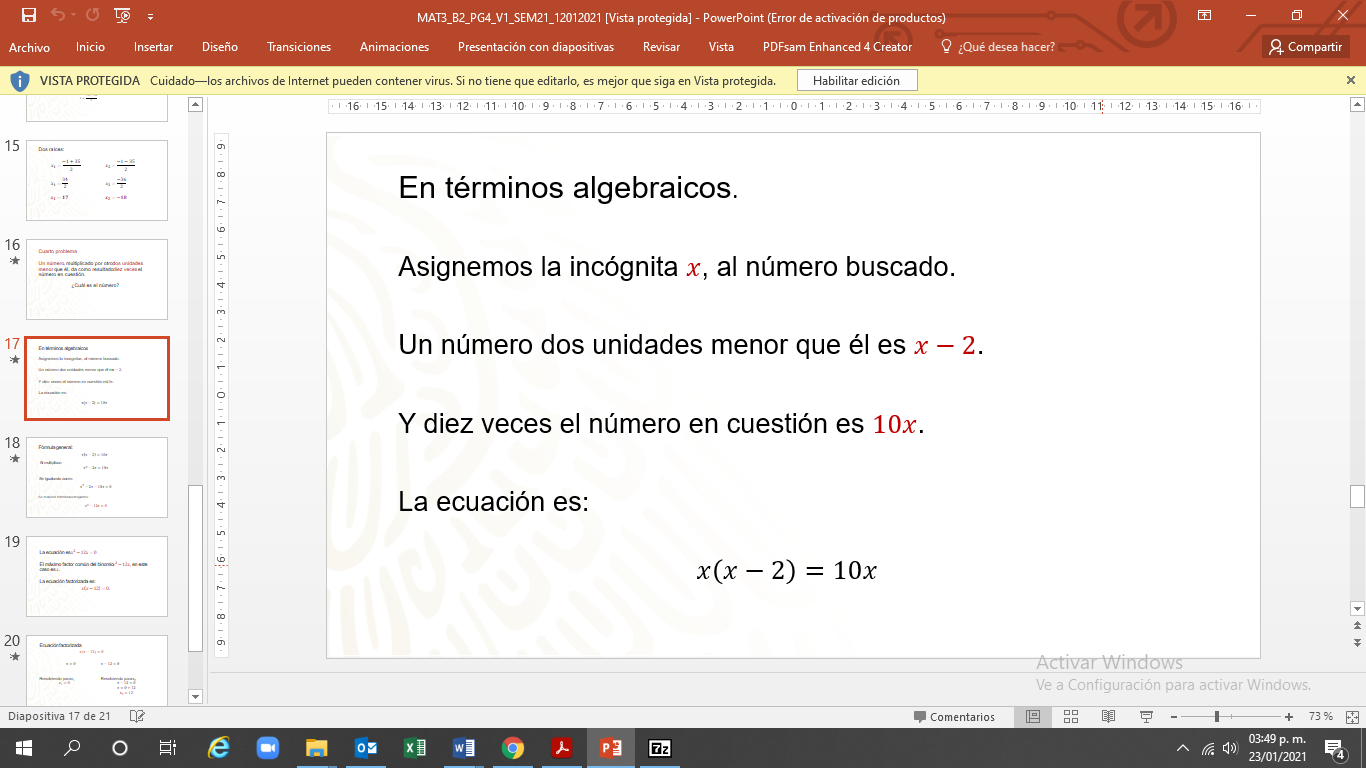
Para simplificar la ecuación, primero, se multiplica “x” por “x” menos 2, es “x” cuadrada. “x” por 2 negativo es 2”x” igual a 10”x”
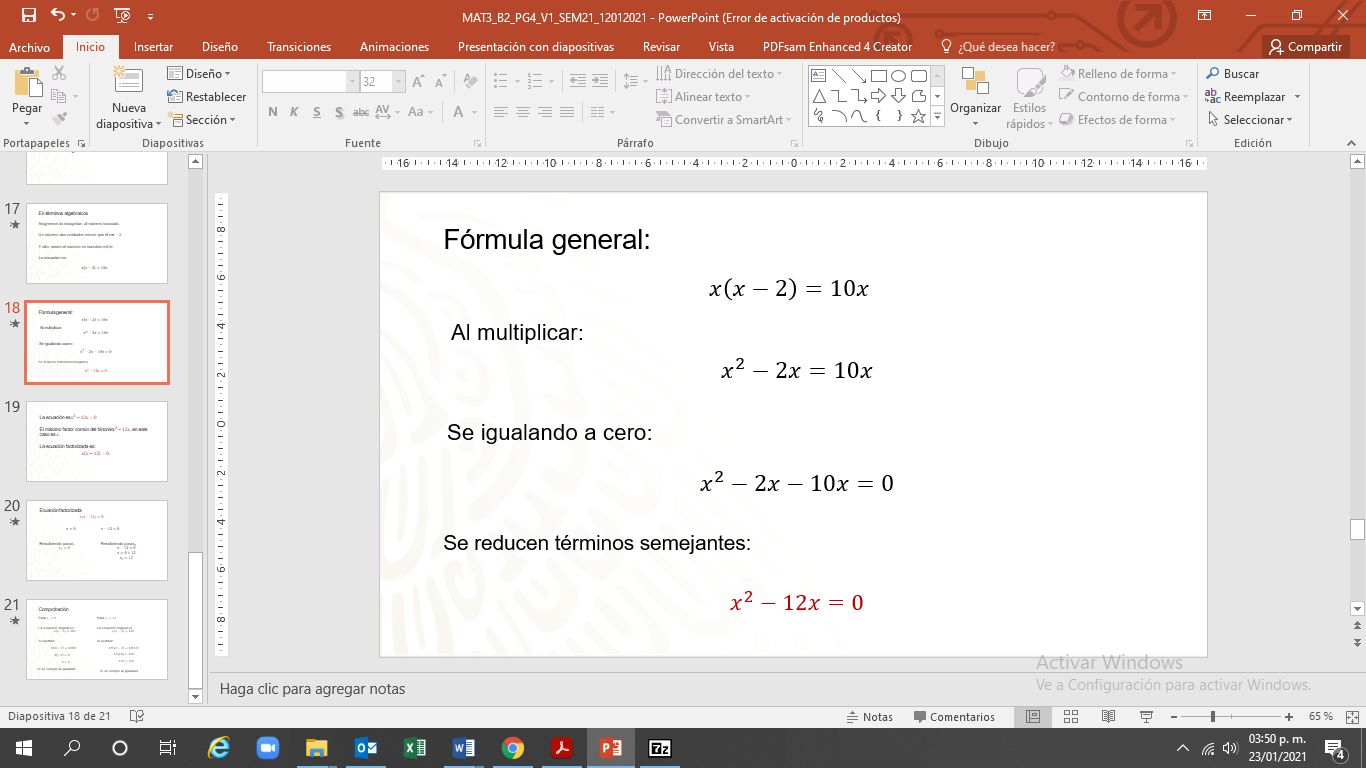
Se iguala a cero, “x” al cuadrado, menos dos “x”, menos diez “x” igual a cero.
Por último, se reducen términos semejantes. La ecuación, simplificada y en la fórmula general es “x” al cuadrado, menos doce “x” igual a cero”.
¿Qué método conviene utilizar para esta ecuación?
La ecuación no se puede resolver despejando. Es una ecuación incompleta.
La ecuación no se puede resolver despejando. Es de la forma “ax” al cuadrado, más “b” “x” igual a cero”.
Este tipo de ecuaciones se pueden resolver por factorización o por fórmula general.
Observa cómo se resuelve por factorización.
En este caso, se factoriza la ecuación buscando el máximo factor común, “x”.
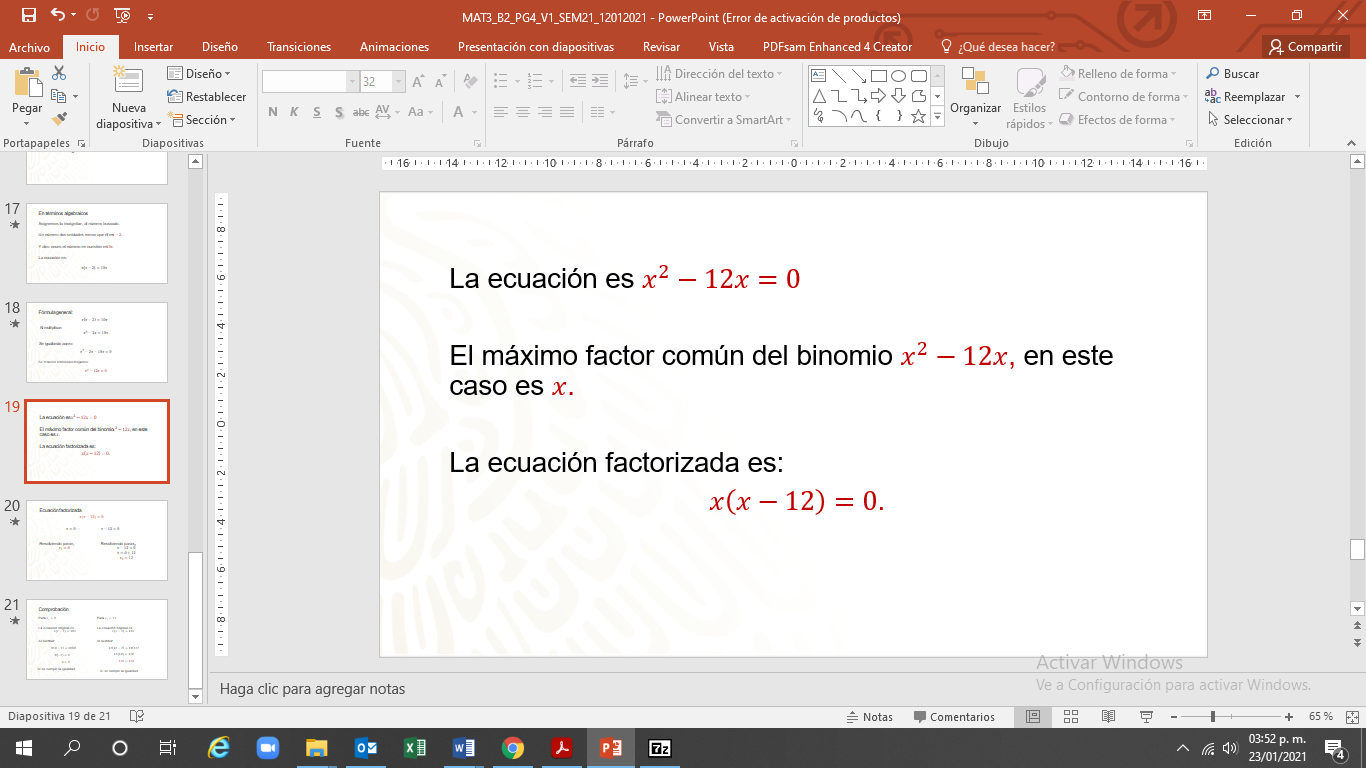
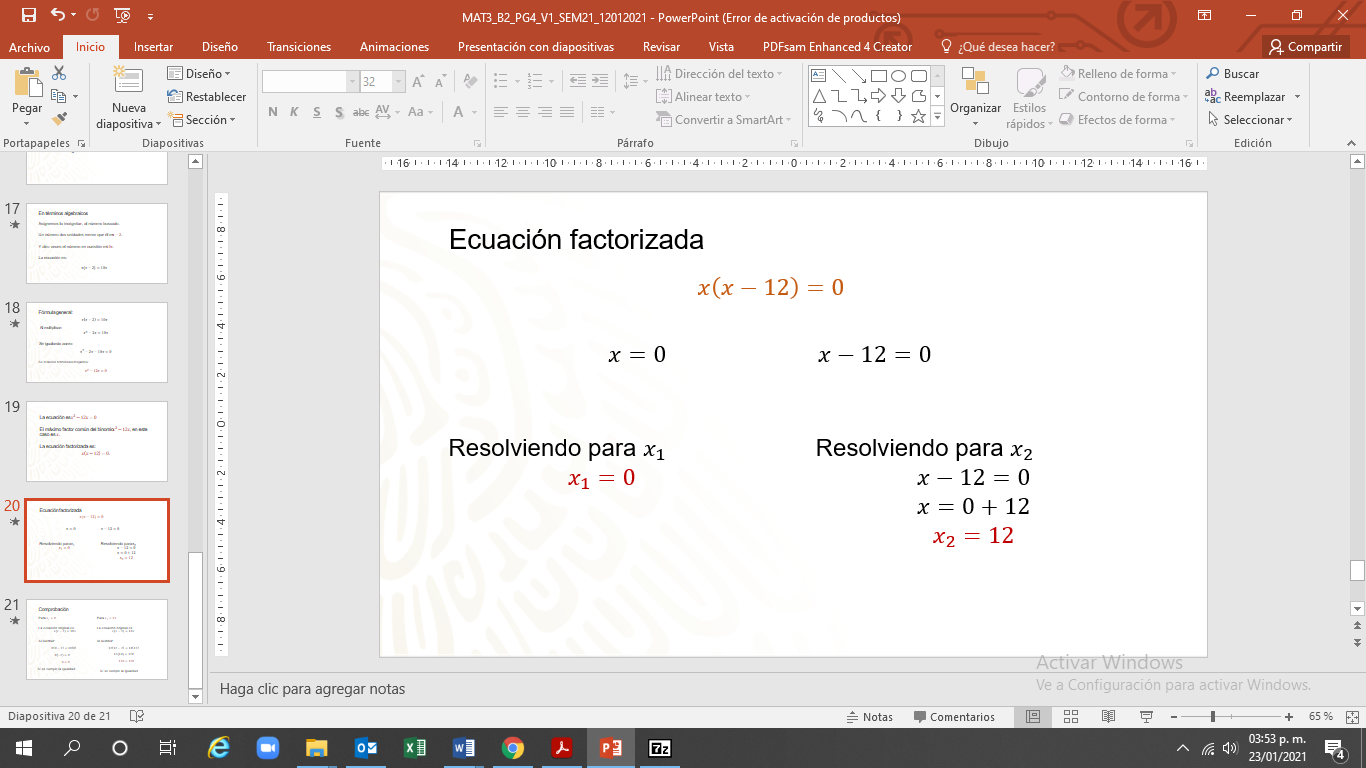
Cada una de las nuevas ecuaciones se iguala a cero y se resuelve por despeje.
La primera ecuación es “x” es igual a cero”
La segunda ecuación es “x” menos 12 igual a cero, se despeja la incógnita y el resultado es “x” igual a 12.
Cero y doce son las raíces de la ecuación.
En este problema no hay restricción respecto a si la solución debe ser positiva o negativa. ¿Cuál es la solución correcta?
El problema pregunta ¿cuál es el número que cumple con las condiciones indicadas? Esta situación tiene dos soluciones. Hay dos números que satisfacen la expresión algebraica del problema.
Al sustituir “x” uno igual a cero” en la ecuación original, se cumple la igualdad.
Si se sustituye “x2” es igual a 12 en lugar de la incógnita en la ecuación original, también se cumple la igualdad.
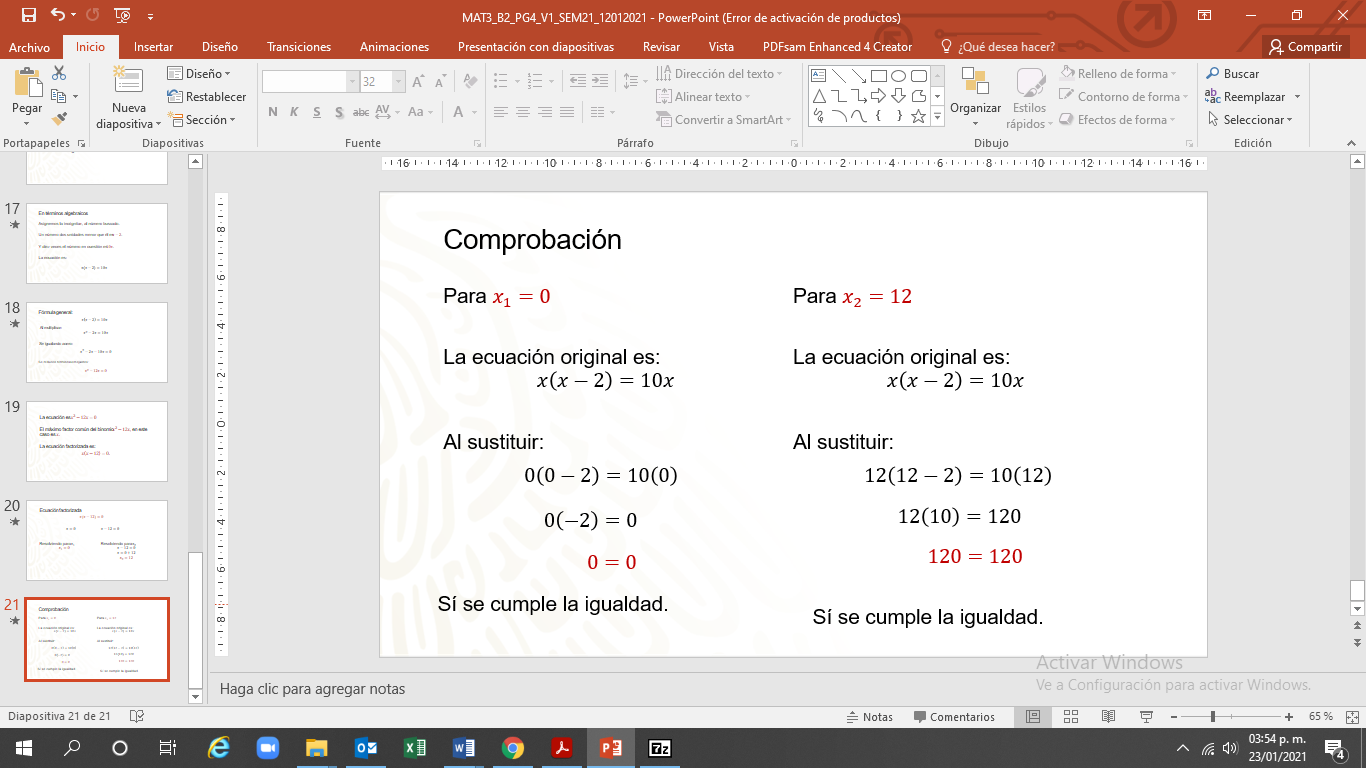
El número que se busca puede ser cero, pero también puede ser doce.
Y con respecto a los métodos para resolver las ecuaciones cuadráticas es importante plantear correctamente la ecuación. Así, se puede elegir el método que más convenga.
En efecto, debes elegir el método que más convenga para simplificar el trabajo y obtener la solución o soluciones correctas de manera eficiente.
El reto de hoy:
Siempre que te sea posible, comparte tus anotaciones con tus compañeros y tu maestra o maestro. Seguramente, socializar tus hipótesis y suposiciones resultará provechoso para consolidar tus conocimientos y los aprendizajes esperados.
Localiza, en las páginas de su libro de texto, las actividades relacionadas con este aprendizaje esperado. Intenta resolver, a partir de lo que aprendiste durante esta sesión, las situaciones que se te proponen.
Una parte importante de la consolidación del aprendizaje es intentar resolver por tu cuenta situaciones afines a las que aquí se presentaron.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas