Medida de probabilidad
Medida de probabilidad
Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: expresar la medida de probabilidad.
¿Qué vamos a aprender?
El propósito de esta sesión es: Resolver problemas que impliquen eventos mutuamente excluyentes e independientes. Para el cual resolverás algunos problemas de la vida cotidiana donde se aplican estas características.
Inicia recordando que la probabilidad mide la frecuencia con la que ocurre un resultado en un experimento aleatorio bajo condiciones suficientemente estables. También que, en un experimento aleatorio, la probabilidad que ocurra un evento aleatorio A es igual al cociente de los casos favorables en los que pueda ocurrir el evento A entre los casos posibles del experimento aleatorio. Se expresa de la siguiente forma.

Considera problemas en donde apliques las características de los eventos mutuamente excluyentes y de los eventos independientes.
¿Qué hacemos?
Observa el siguiente video que refiere las características de los eventos mutuamente excluyentes.
- ¿Cuándo dos eventos son mutuamente excluyentes?
https://youtu.be/Ig6Ei3H2Sjg
Para poder determinar el que dos eventos sean mutuamente excluyentes, en esencia es que ocurra uno u el otro, pero no los dos al mismo tiempo. Observa ahora un problema que involucra este tipo de eventos.
El experimento aleatorio es lanzar un dado y una moneda al mismo tiempo.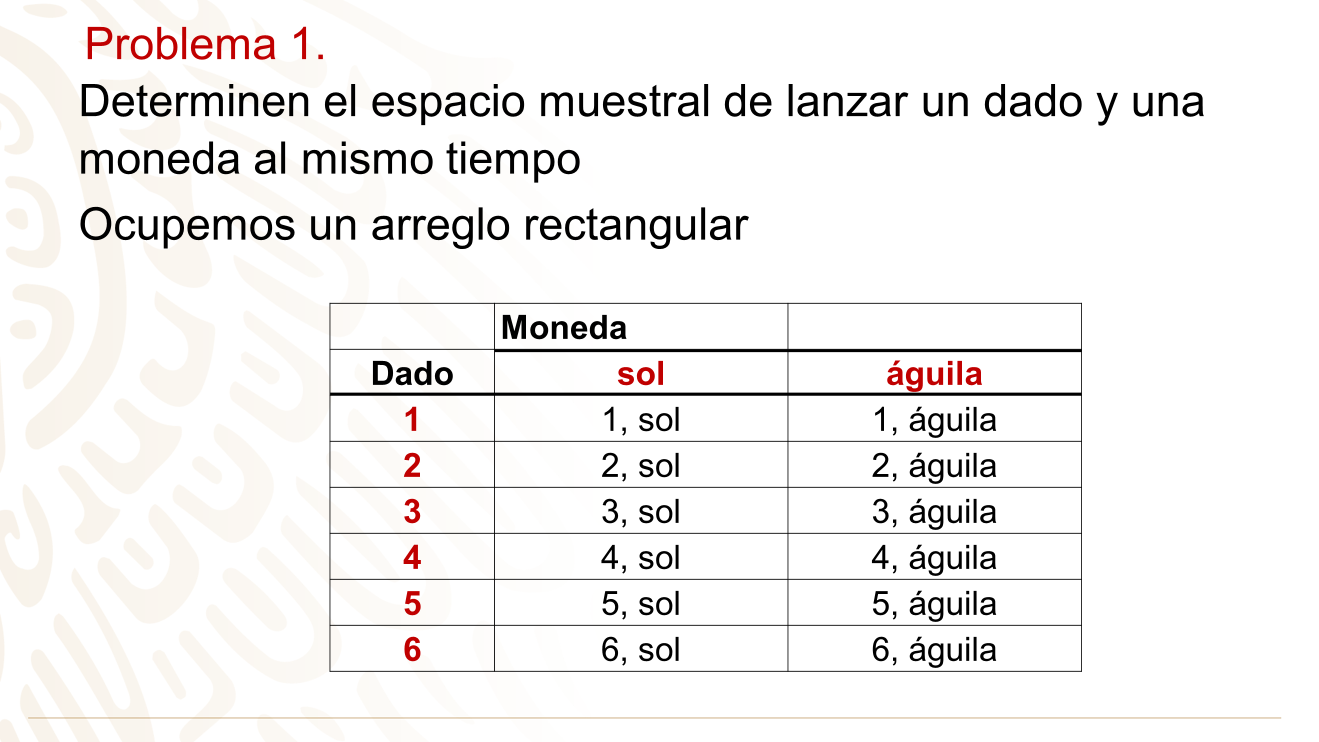
El espacio muestral es: 𝑆 = [1𝑠, 2𝑠,3𝑠,4𝑠,5𝑠,6𝑠,1𝑎,2𝑎,3𝑎,4𝑎,5𝑎,6𝑎]
Y su cardinalidad es: 12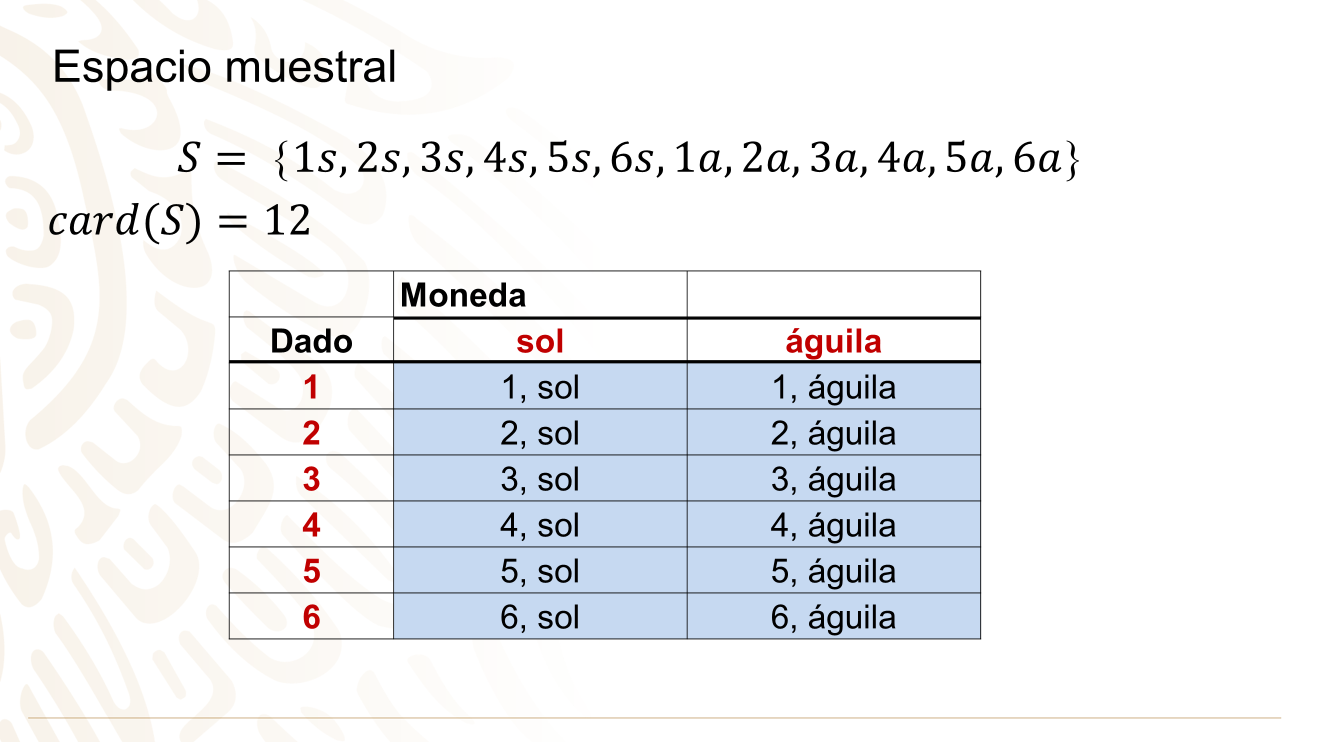
Considerando el espacio muestral, llena los datos que faltan en la siguiente tabla.
En la tabla se enuncia un evento, el evento A, que es que caiga un número par y sol.
Se observan los resultados posibles del mismo, que son [2águila, 4águila y 6águila] y se obtiene su probabilidad que 3 doceavos, que es también un cuarto, que es igual a 0.25, igual a 25%. Complétala:
¿Cómo definirías al evento B? ¿y su probabilidad?
Observa cuáles son los posibles resultados del evento: 2 águila, 4 águila y 6 águila.
B es el evento: Cae un número par y águila y su probabilidad es 3 doceavos
¿Cuáles son los resultados posibles del evento C? ¿Y su probabilidad?
Son (4a, 5a, 6a), pues son mayores que 3 y sale águila y su probabilidad es 3 doceavos
¿Cuáles son los resultados posibles del evento D? ¿Y su probabilidad?
Son (1s, 3s, 5s), pues son impares y sale sol y su probabilidad es 3 doceavos
¿Cómo definirías al evento E? ¿y su probabilidad?
Observa cuáles son los posibles resultados del evento: 1águila, 2águila y 3águila. El evento E es cae un número menor o igual a 3 y águila y su probabilidad es 3 doceavos
¿Cómo definirías al evento F? ¿y su probabilidad?
Observa cuáles son los posibles resultados del evento: 4 sol, 5 sol y 6 sol. El evento F es Cae un número mayor a 3 y sol y su probabilidad es 3 doceavos
Ya está completa la tabla. Ahora puedes hacerte algunas preguntas. Compara los eventos A y F ¿tienen elementos en común? ¿Qué los hace diferentes?
Recuerda los resultados posibles del evento A y de evento F. Sí tienes elementos en común 4s y 6s. Difieren en 2s y 5s.
¿Pueden darse al mismo tiempo los eventos E y F? ¿Cuál es la probabilidad de que ocurra uno u otro?
Puedes ver que no comparten elementos. Pero la probabilidad de que ocurra uno y otro al mismo tiempo, es cuando comparten elementos. La cardinalidad de eso es 0, por lo tanto, la probabilidad es 0.
¿Puede darse al mismo tiempo los eventos A y B? ¿Cuál es la probabilidad de que ocurra uno u otro?
Pero la probabilidad de que ocurra uno y otro a la vez es cuando comparten elementos. La cardinalidad de eso es 0, por lo tanto, la probabilidad es 0
Reflexiona: ¿Qué significado puede tener el hecho de que dos eventos tengan elementos comunes? ¿Y al hecho de que dos eventos no tengan elementos comunes?
Piensa en ello.
Dos eventos que no pueden ocurrir a la vez. De hecho, si se cumple uno, no se cumple el otro. Son eventos mutuamente excluyentes. Y como viste, la probabilidad de que ocurran los dos la vez es 0.
Repasa sobre los eventos Independientes y cómo se identifican, para así poder determinar la probabilidad de ocurrencia en un experimento.
Observa el siguiente video: - ¿Cuándo dos eventos son independientes?
https://nuevaescuelamexicana.sep.gob.mx/detalle-recurso/1438
Observa un problema que involucra este tipo de eventos.
En un juego, se lanzan cuatro volados consecutivos y en todos ellos cae sol.
¿Cuál es la probabilidad de que en el quinto volado también caiga sol?
¿Los resultados de los cuatro primeros volados afectan el resultado del quinto?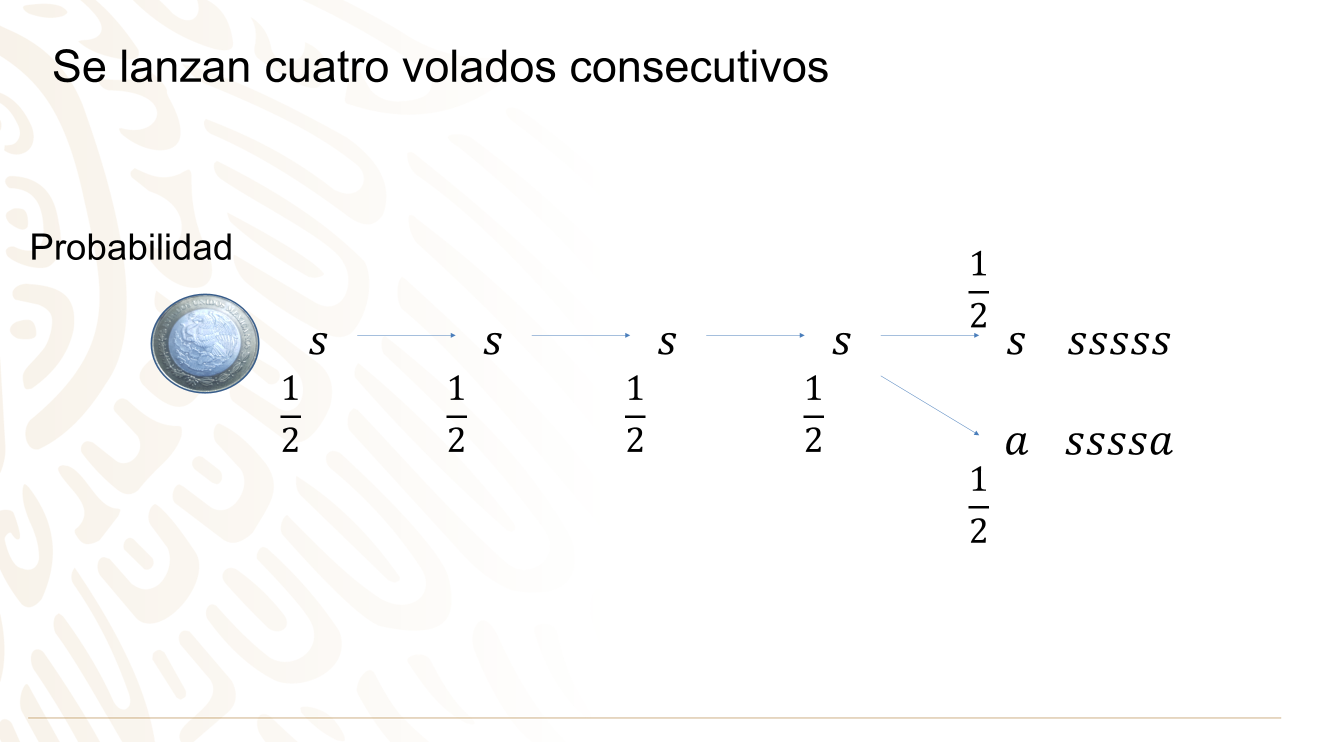
¿Cuál es el espacio muestral de cada volado?
El espacio muestral en cada volado es el mismo: para el primer volado es [sol, águila], para el segundo volado es [sol, águila], para el tercer volado es [sol, águila], y para el cuarto volado es [sol, águila]. ¿Cuál es el espacio muestral para el quinto volado?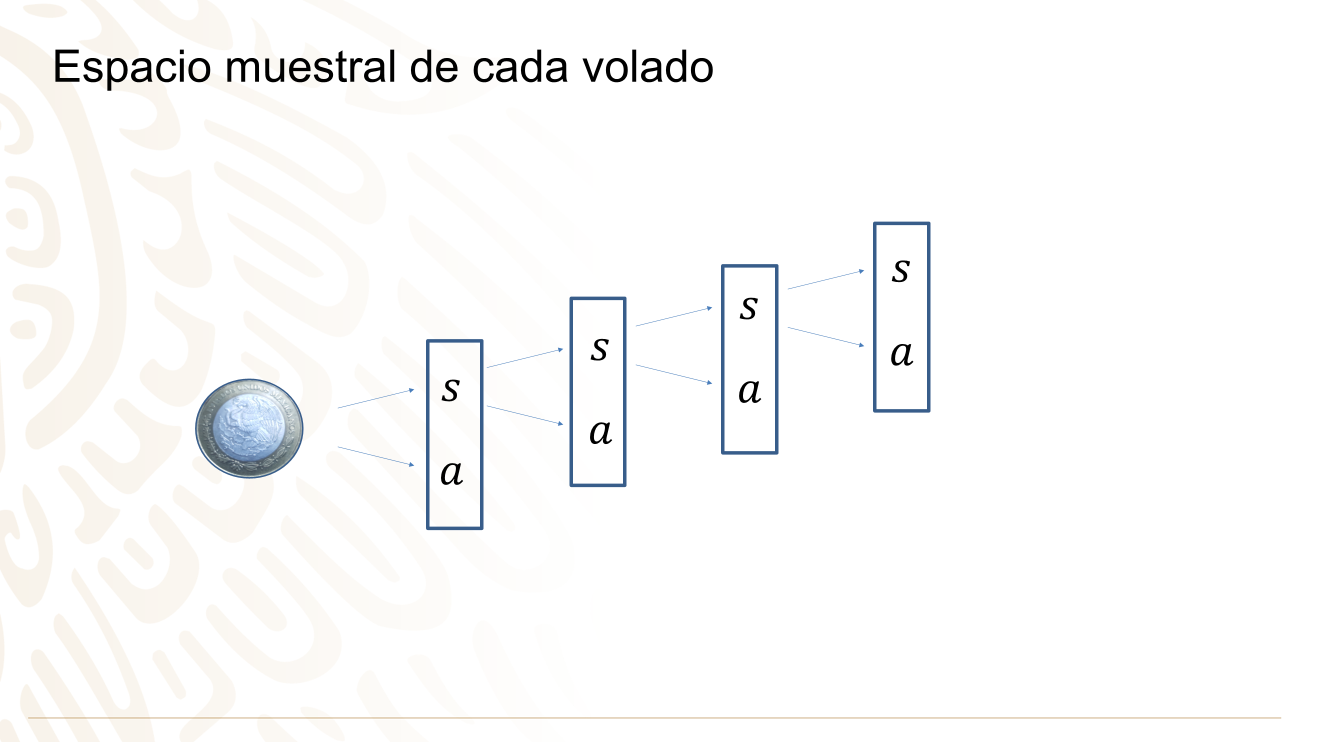
Piensa en esto: ¿La probabilidad de ocurrencia de un evento influye en la probabilidad de que suceda nuevamente al repetir el experimento n veces, como en el caso de la moneda?
Analiza la pregunta y anota el resultado en tu cuaderno.
Observa otra situación.
En una urna se tienen 5 fichas: una verde, una amarilla, una azul, una negra y una roja. ¿Cuál es la probabilidad de sacar la ficha negra? Es un quinto.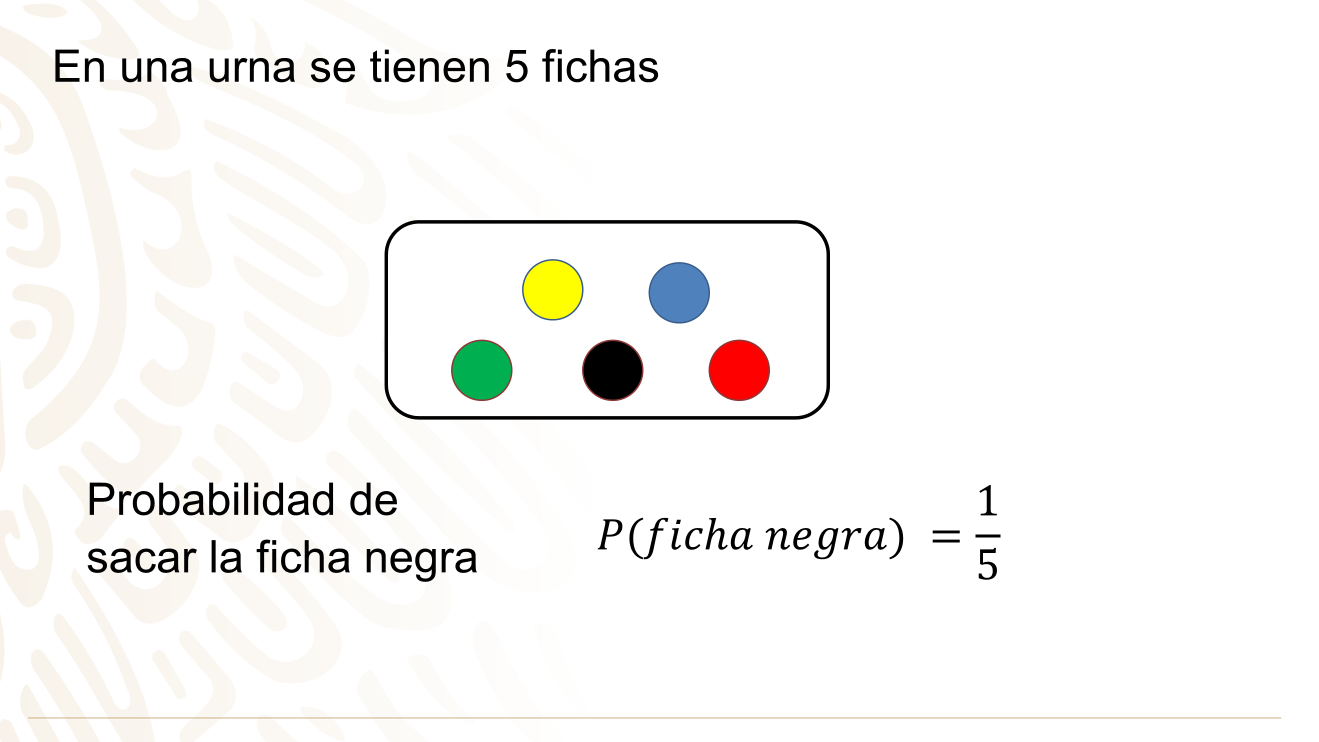
Sin ver se saca una ficha. Si se extrae la ficha negra y no se regresa la urna.
¿Cuál es la probabilidad de sacar la ficha verde en la segunda extracción? Es un cuarto.
Como puedes observar la probabilidad cambia. ¿Por qué ocurre esto?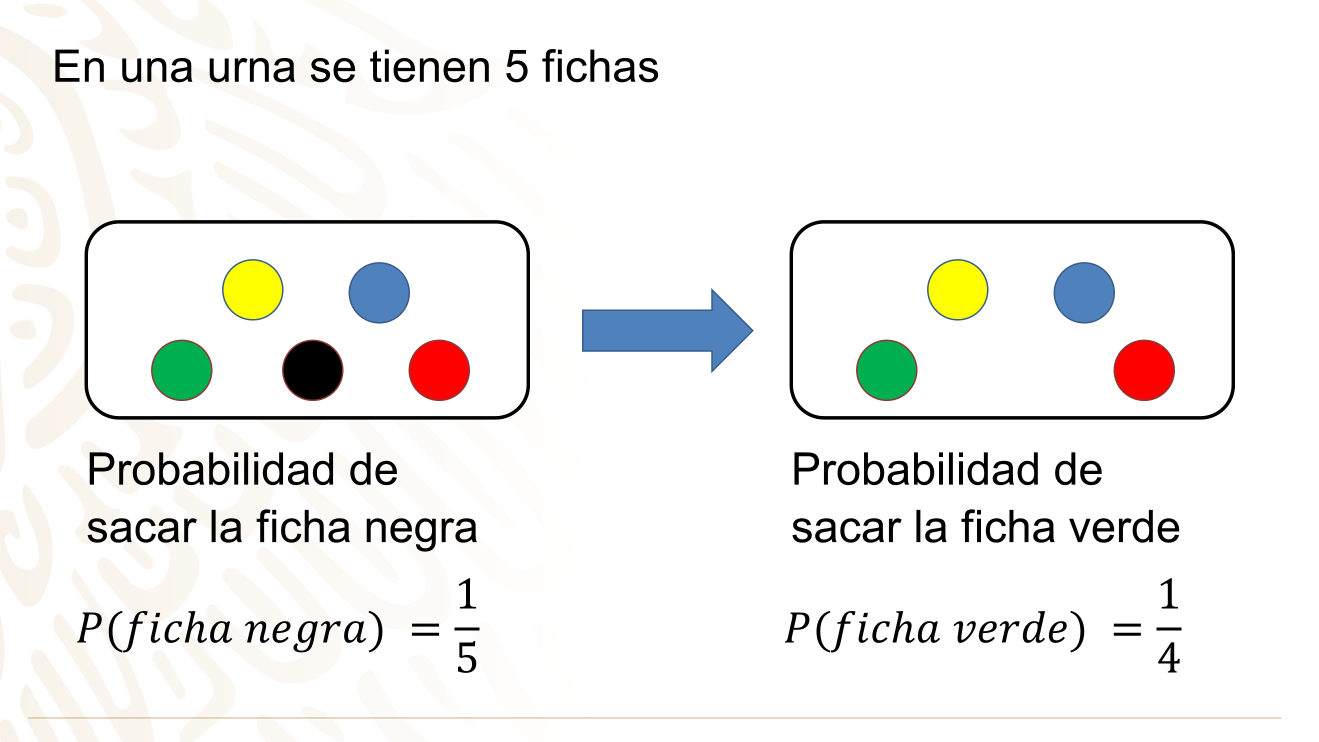
Observa: ¿Este resultado se ve afectado por la primera extracción? Sí. El espacio muestral cambia. Esto era algo que no pasaba con los lanzamientos de moneda.
Si se extrae la ficha negra y se regresa a la urna y en la segunda extracción sale la ficha azul y se regresa, y en una tercera nuevamente sale la negra y se regresa. ¿Qué probabilidad hay de sacar la ficha amarilla en una cuarta extracción?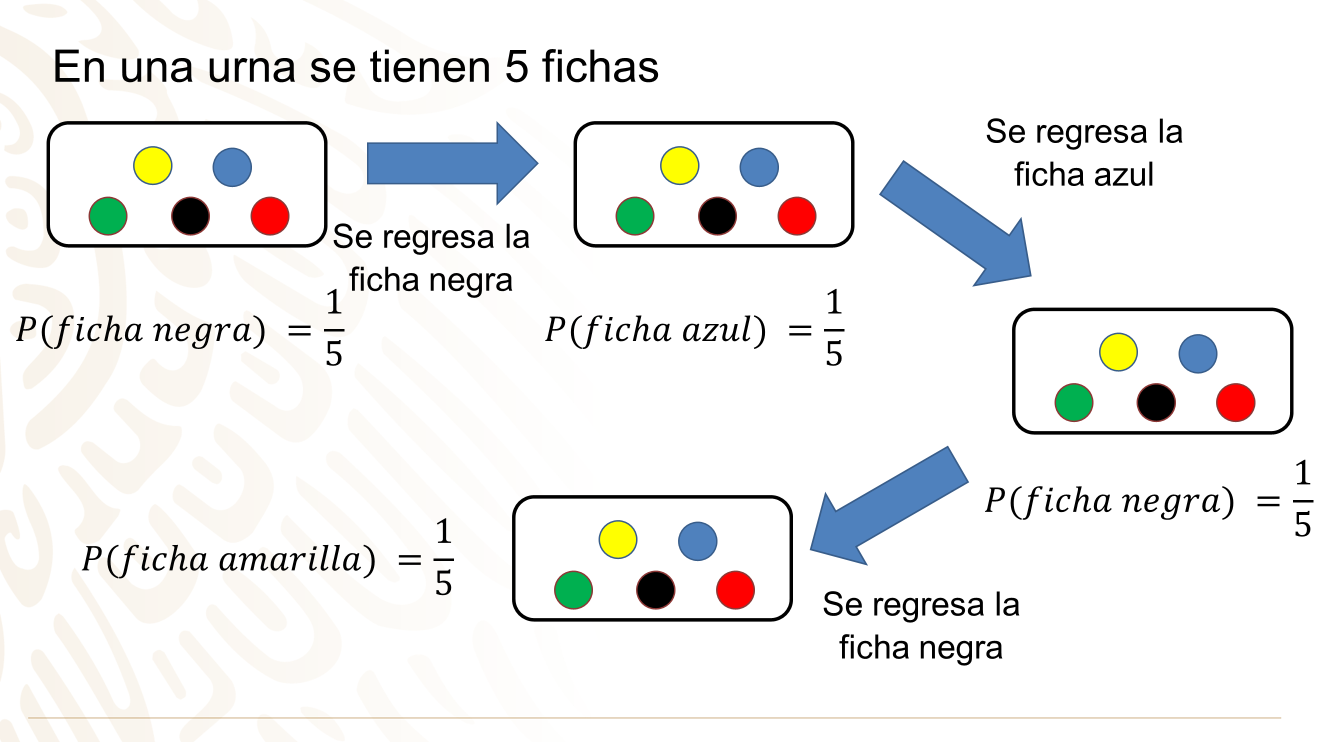
Reflexiona: En el caso de la urna, el hecho de extraer y regresar una ficha no afecta el resultado de la siguiente toma; la probabilidad de cada evento sigue siendo la misma.
¿Qué significado puede tener el hecho de que la probabilidad permanezca igual? Piensa en ello.
Cuando la ocurrencia de un evento no afecta la ocurrencia de otro evento. Son eventos independientes.
Observa el siguiente video del minuto 4:20 al 6:09 y del minuto 6:23 al 8:11. - Probabilidad y eventos independientes
Observa la solución a retos y preguntas que se plantearon en sesiones anteriores.
En la sesión sobre: “Resolver problemas que impliquen las propiedades de semejanza de triángulos”.

Se mencionan 3 retos, estos son:
El primer reto: ¿Te acuerdas del personaje que se mencionó en el video? Aquel que, sin hacerlo directamente, sino que, por medio de la triangulación, de la proyección de su sombra y la altura de una persona conocida como datos, y una operación sencilla midió la altura de la gran pirámide de Egipto.
La respuesta a este reto es: en el siglo VI, el filósofo griego Tales, midió por la pirámide de Keops mediante semejanza de triángulos.
El segundo reto: al final del ejercicio del “Teorema de Napoleón”, donde se demuestra la semejanza de triángulos equiláteros, a partir de un triángulo escaleno.
¿Porque se llama Teorema de Napoleón?


Después del reto anterior, siguieron las siguientes preguntas:


El reto de hoy:
Aprendiste a resolver problemas aplicando las características de los eventos mutuamente excluyentes y eventos independientes, aplicado en problemas.
Te sugerimos revisar en tu libro de texto y resuelvan los problemas que tienen estas características, comparte tus resultados con tus compañeros y llega a una conclusión.
Recuerda lo que dijo Galileo en su libro El ensayador:
“El verdadero conocimiento está escrito en un enorme libro, abierto continuamente ante nuestros ojos, me refiero al universo.
Pero uno no puede entenderlo, uno debe aprender la lengua y reconocer los caracteres para poder entender el lenguaje en el que está escrito. Está escrito en el lenguaje de las matemáticas”
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: