Mediatriz y bisectriz
Mediatriz y bisectriz
Aprendizaje esperado: explora características y propiedades de figuras y cuerpos geométricos.
Énfasis: resolver problemas que impliquen el uso de las propiedades de la mediatriz de un segmento y la bisectriz de un ángulo.
¿Qué vamos a aprender?
Se te pide tener a la mano tu cuaderno, lápiz, escuadra, compás y goma.
El uso de las propiedades de rectas, como la mediatriz de un segmento y la bisectriz de un ángulo, son herramientas útiles en la solución de problemas geométricos.
¿Qué hacemos?
Comienza con la mediatriz de un segmento, que se define como la línea recta perpendicular a dicho segmento trazada por su punto medio.
En el segmento de recta AB, el punto P es el único punto que pertenece al segmento de recta y que se encuentra a la misma distancia de los puntos extremos A y B. De este modo, el punto P es el punto medio del segmento.
La línea recta perpendicular al segmento de recta AB que pasa por el punto medio P es la mediatriz.
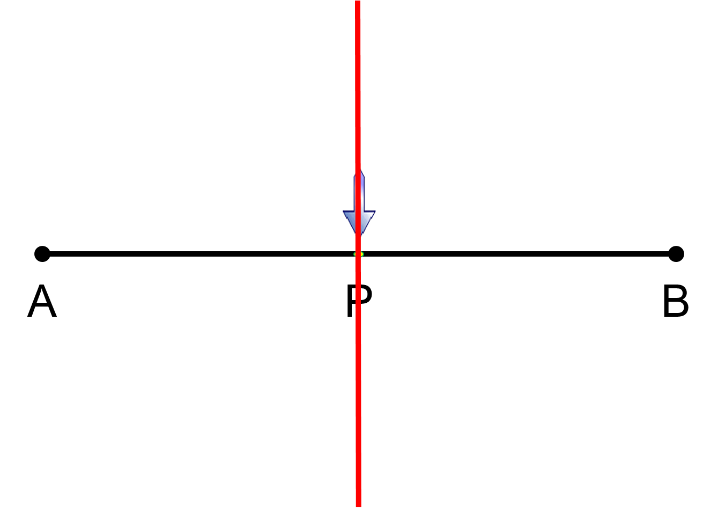
Trázala con la ayuda de la regla y del compás.
Apoya el compás en un extremo del segmento (punto A) y se abre a una distancia mayor que la mitad del mismo segmento.
Después se traza un segmento de circunferencia. Se apoya el compás en el otro extremo del segmento (punto B) y se traza un segmento de circunferencia con el mismo radio que el anterior.
Y, finalmente, con la regla se unen los puntos de intersección C y D de los segmentos de circunferencia para obtener la mediatriz.
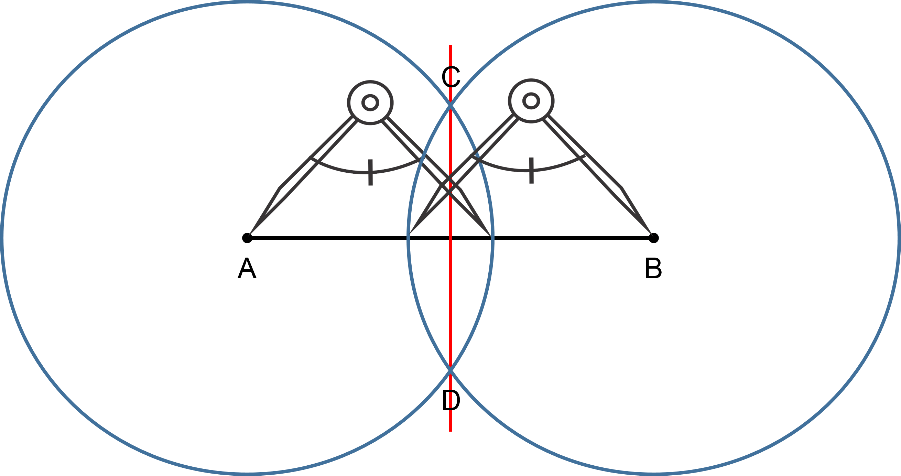
La mediatriz también tiene como características que cualquier punto en ella se encuentra a la misma distancia de los puntos extremos A y B.
Otra forma en la que puedes obtener la mediatriz de un segmento es con escuadras y una regla graduada.
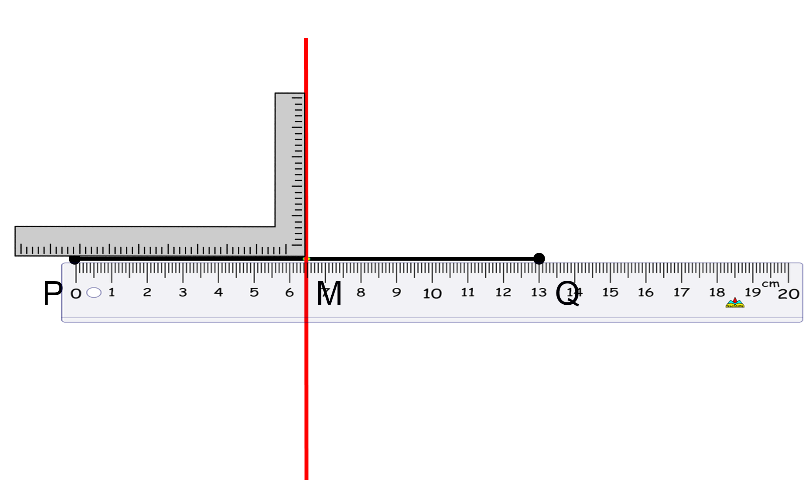
Por ejemplo, dado el segmento de recta PQ, se localiza el punto medio M usando la regla para medir el segmento y dividirlo en dos.
En este caso, el segmento tiene 13 centímetros y el punto medio M se indica a 6.5 centímetros.
Con las escuadras se traza una perpendicular al segmento PQ, usando el ángulo de 90 grados y que pase por el punto M.
Y, finalmente, se extiende la recta en ambos sentidos para obtener la mediatriz del segmento PQ.
Una de las propiedades de esta recta es que cualquier punto sobre la mediatriz se encuentra a la misma distancia de los extremos del segmento; es decir que es equidistante, lo que se emplea en la solución de diversos problemas y situaciones.
En el segmento anterior se puede escoger de forma aleatoria cualquier punto sobre la mediatriz, y éste tiene la misma distancia hacia los puntos P y Q.
Este punto R se encuentra a 10 cm de P y a 10 cm de Q.
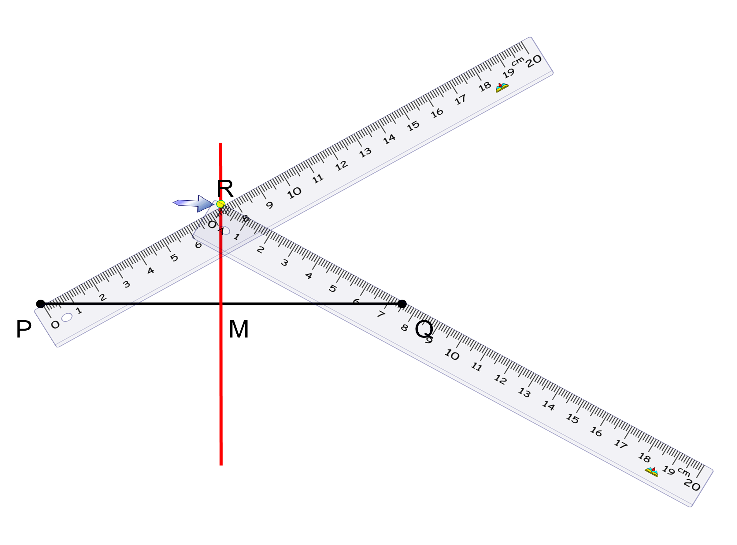
Del mismo modo, este otro punto, S, también pertenece a la mediatriz, y su distancia hacia P es de 15 cm, y su distancia hacia Q también es de 15 cm.
En conclusión, no existen puntos fuera de esa recta que cumplan la condición de estar a la misma distancia de los extremos P y Q.
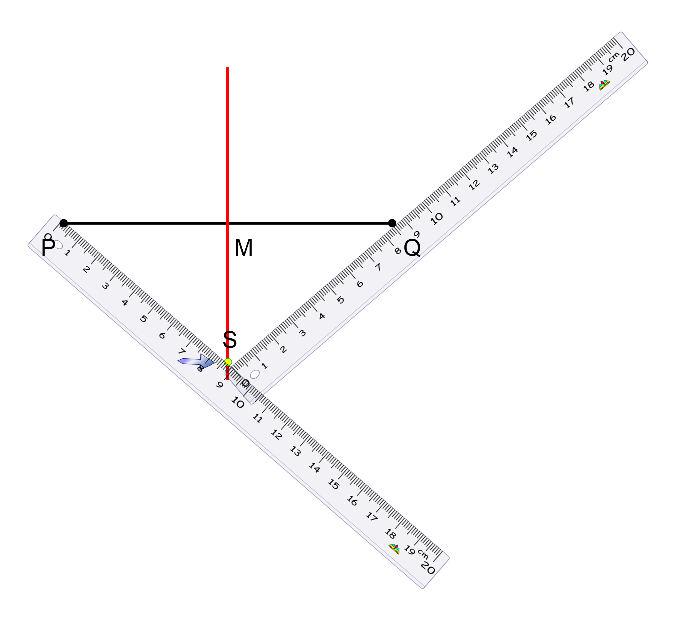
Es de notar que la mediatriz es una recta, por lo que se extiende en ambas direcciones de forma infinita.
Otra propiedad de la mediatriz es que forma un ángulo de 90 grados con el segmento de recta. Dicho de otra manera, un segmento de recta y su mediatriz son perpendiculares.
Con base en lo anterior, se tiene que:
Los puntos A, B y C representan la ubicación de tres poblados diferentes para los que se desea construir un hospital que esté a la misma distancia de los tres poblados.
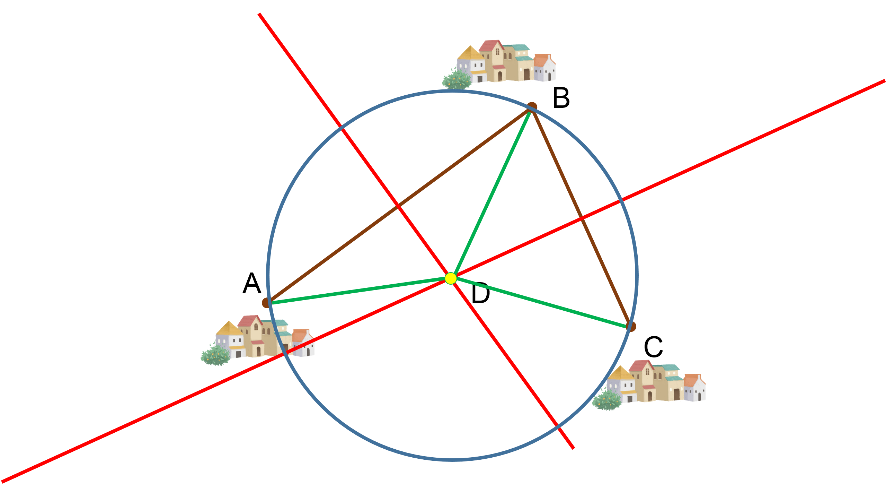
Pero ¿en dónde se le debe localizar al punto D que representa al hospital?
Para resolverlo, se debes unir con un segmento los poblados A y B; se traza la mediatriz del segmento AB para tener todos los puntos que están a la misma distancia de esos dos poblados.
Del mismo modo se hace para los poblados B y C, y se traza la mediatriz del segmento BC.
Al tener ya trazadas las dos rectas mediatrices, se obtiene el punto de intersección de ambas, lo que significa que sí existe un punto en común que está a la misma distancia del poblado A y del poblado B, y al mismo tiempo, está a la misma distancia del poblado B y del poblado C.
Al punto de intersección de las dos mediatrices se le denomina circuncentro y tiene la característica de ser equidistante con los 3 puntos.
Si se traza un círculo con centro en D hasta el punto A, se puede observar que la distancia a cada poblado es la misma, ya que son radios de la misma circunferencia.
De este modo, se demuestra que el uso y conocimiento de la mediatriz permite dar respuesta a situaciones como la anterior.
Trabaja ahora situaciones con bisectrices.
La bisectriz de un ángulo es la recta que pasa por el vértice del ángulo y determina dos ángulos iguales.
Asimismo, la bisectriz es el eje de simetría del ángulo.
Además, el segmento de recta perpendicular desde un punto de un lado que forma al ángulo, hacia la bisectriz, será equidistante a su segmento simétrico.
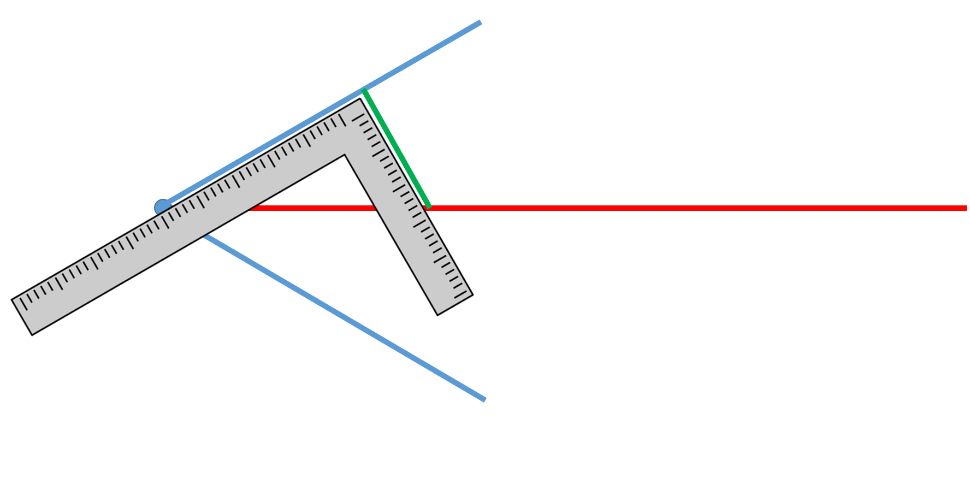
Ahora observa cómo se traza la bisectriz de un ángulo.
Se apoya el compás en el vértice del ángulo (punto O) y se realiza una marca a la misma distancia en los segmentos que forman el ángulo.
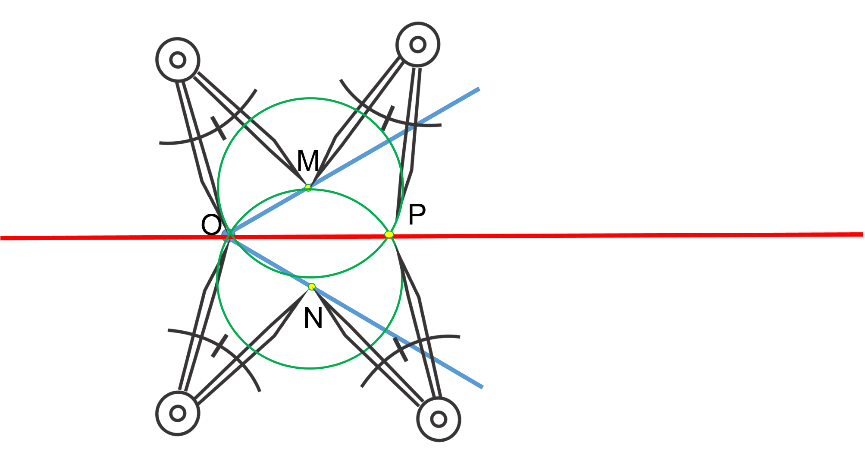
Con este paso, se tienen localizados dos puntos, M y N, que son equidistantes al vértice.
Se apoya el compás en M y se traza un arco de circunferencia; se tiene cuidado de que la abertura del compás sea adecuada, que significa que sea mayor a la abertura del ángulo.
Después se apoya el compás en N y, con la misma abertura, se encuentra el punto de intersección P con el último arco trazado.
Por último, se une el vértice O del ángulo con el punto P y se obtiene así la bisectriz del ángulo.
A continuación, se usa la bisectriz de un ángulo para la construcción que explora las relaciones de un triángulo y sus ángulos internos y externos.
El ejercicio se construye de la siguiente manera:
En el triángulo ABC se traza la bisectriz del ángulo alfa y la bisectriz del ángulo gamma, que es el ángulo exterior del triángulo.
Al punto de intersección de las dos bisectrices lo nombramos D y con éste se forma el triángulo ACD.
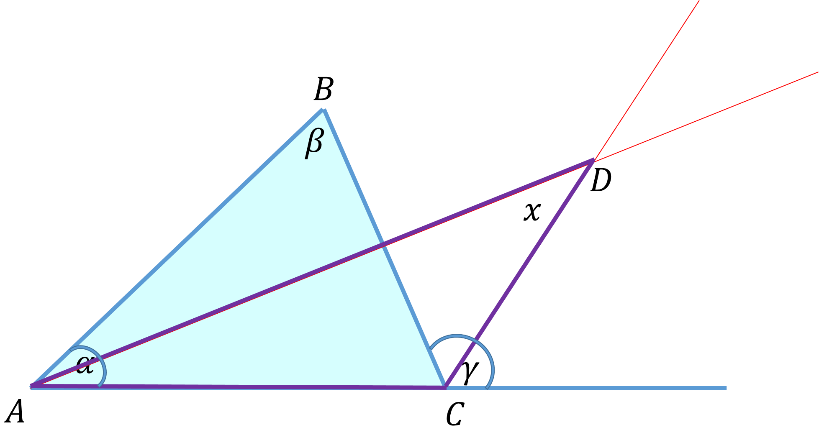
Ante este caso, la pregunta es: ¿cuál es el valor del ángulo “x” en el vértice D?
Analizando el diagrama y empleando la información que se obtiene del enunciado, el triángulo ABC tiene de ángulo en el vértice A el valor de alfa, y beta, el valor del ángulo en el vértice B. Además, el valor del ángulo externo en el vértice C vale gamma.
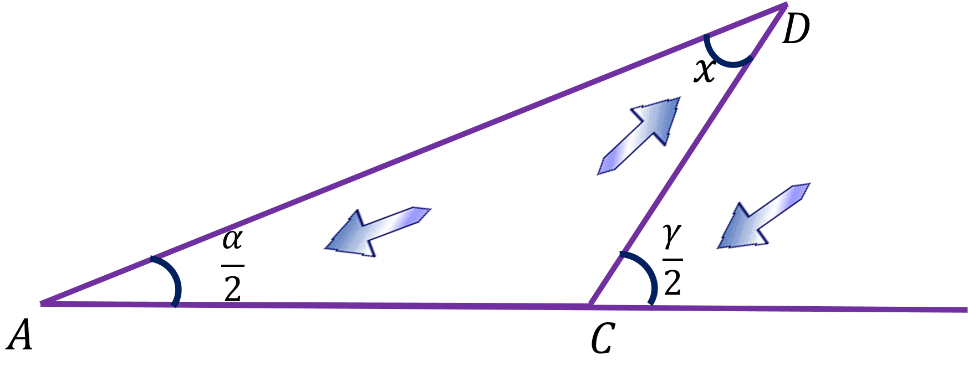
Para el triángulo ADC, el valor del ángulo en el vértice A es de “alfa medios” porque el segmento AD se construye bisectriz del ángulo alfa y el ángulo en el vértice D, no lo conoces y por el momento se le asigna el valor de “x”.
Además, el segmento CD es mediatriz del ángulo gamma que, en consecuencia, el ángulo exterior del triángulo ADC en el vértice C tiene un valor de “gamma medios”.
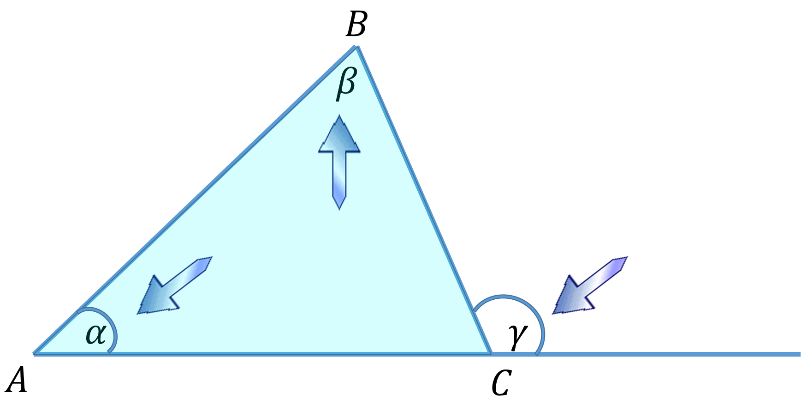
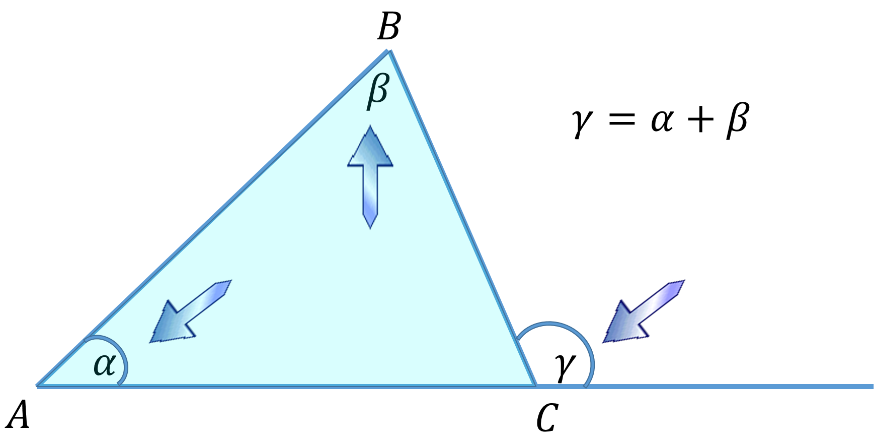
Con respecto al ángulo exterior de un triángulo, se toma en cuenta que su valor es igual a la suma de los dos ángulos interiores no adyacentes a éste, lo que puedes comprobar si analizas que la suma de los ángulos interiores de un triángulo es igual a 180 grados, siendo así suplementarios, al igual que un ángulo interior y el exterior del triángulo en el mismo vértice son también suplementarios, de ahí su equivalencia.
Lo anterior, como se demuestra, es una relación de igualdad que involucra a la incógnita “x” y que permite encontrar su valor.
Centra tu atención en el triángulo ABC y en su ángulo exterior gamma, cuyo valor es igual a la suma de los dos ángulos interiores no adyacentes, en este caso, alfa más beta.
En un segundo análisis, el triángulo ADC tiene como ángulo exterior en el vértice C un ángulo con valor de “gamma medios”, que es igual a sus correspondientes ángulos interiores no adyacentes. Para este caso, son “alfa medios” más “x”.
Al despejar el valor de gamma, se obtiene que es igual a alfa más 2x.
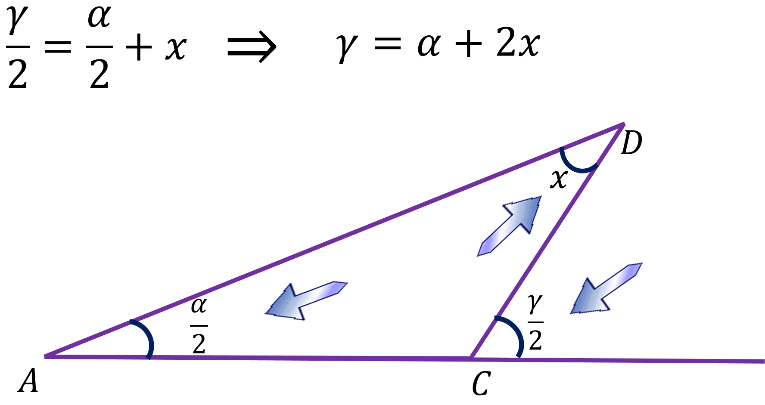
Se realiza el trabajo algebraico correspondiente con las dos igualdades para encontrar el valor de “x”.
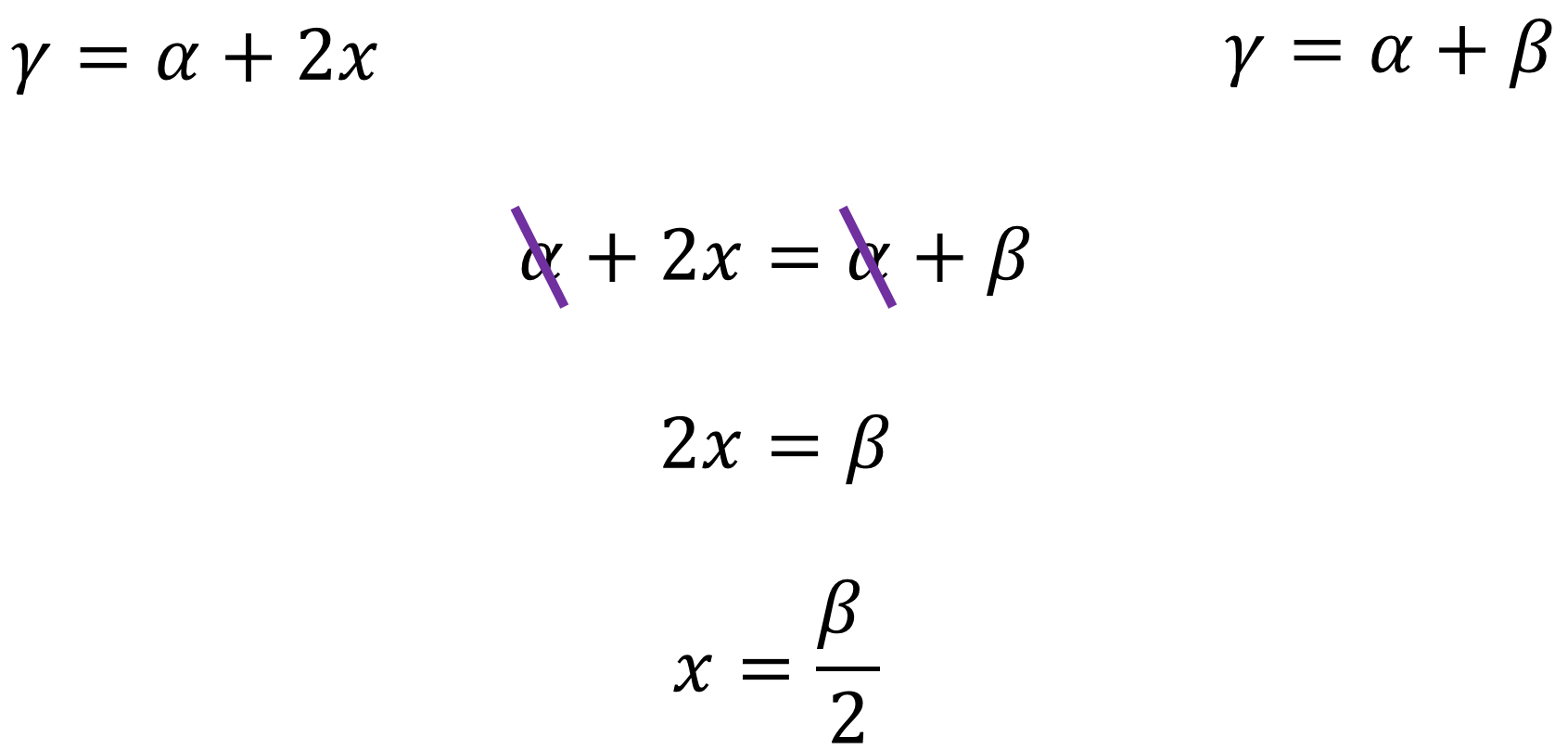
Por un lado, se sabe que el valor de gamma es igual a alfa más beta, mientras que, en la otra igualdad, gamma es igual a alfa más 2x.
Se igualan las dos expresiones y se tiene que alfa más 2x es igual a alfa más beta. Y despejando el valor de “x”, se obtiene que es igual a “beta medios”.
Así, se ha resuelto la pregunta: ¿cuál es el valor del ángulo “x” en el vértice D si se tiene que es la mitad del valor del ángulo beta?
Se observa que esta condición siempre se va a cumplir para cualquier triángulo, así como del triángulo generado con la intersección de las bisectrices de alfa y gamma.
Para comprobar lo anterior, se asignan diferentes valores para alfa y beta.
Para alfa igual a 44 grados y beta igual a 70 grados.
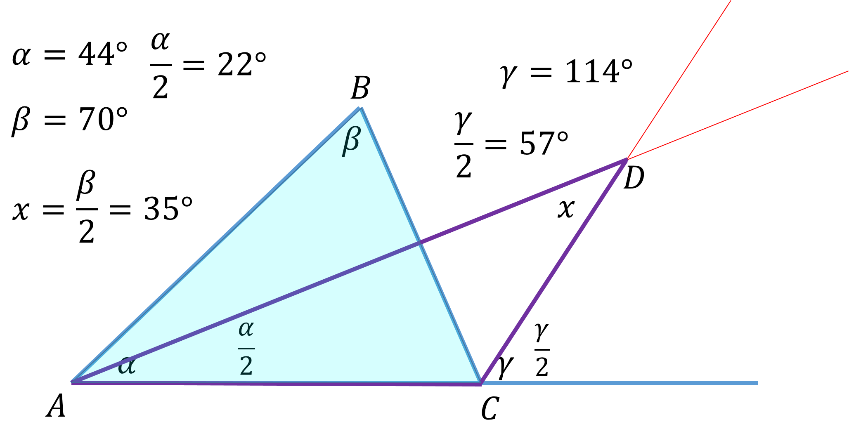
En el triángulo ABC se calcula el ángulo exterior en el vértice C, que es gamma con la suma de los ángulos interiores no adyacentes. Para ello se suman alfa y beta, que es igual a 114 grados.
Para el triángulo ADC, formado con las bisectrices, se considera que el ángulo exterior en el vértice C es “gamma medios”, que es igual a la suma de los dos interiores no adyacentes, que es “alfa medios” más “x”, es decir, la incógnita que se busca calcular.
Entonces, “alfa medios” es igual a 22 grados y “gamma medios” es igual a 57 grados; “x” es igual a 57 menos 22 grados, que es 35 grados.
Así, el valor de “x” es 35 grados, que es la mitad del ángulo beta que tiene un valor de 70 grados.
Traza un triángulo con las medidas que quieras; traza las bisectrices de los ángulos e, igual que en el ejercicio anterior, encuentra el punto de intersección en ambas bisectrices y verifica que el ángulo en el vértice de intersección cumpla con ser la mitad del ángulo beta.
Otro caso por analizar es la cantidad de mediatrices y bisectrices en polígonos regulares.
Ambas rectas tienen coincidencia con el eje de simetría de los polígonos regulares.
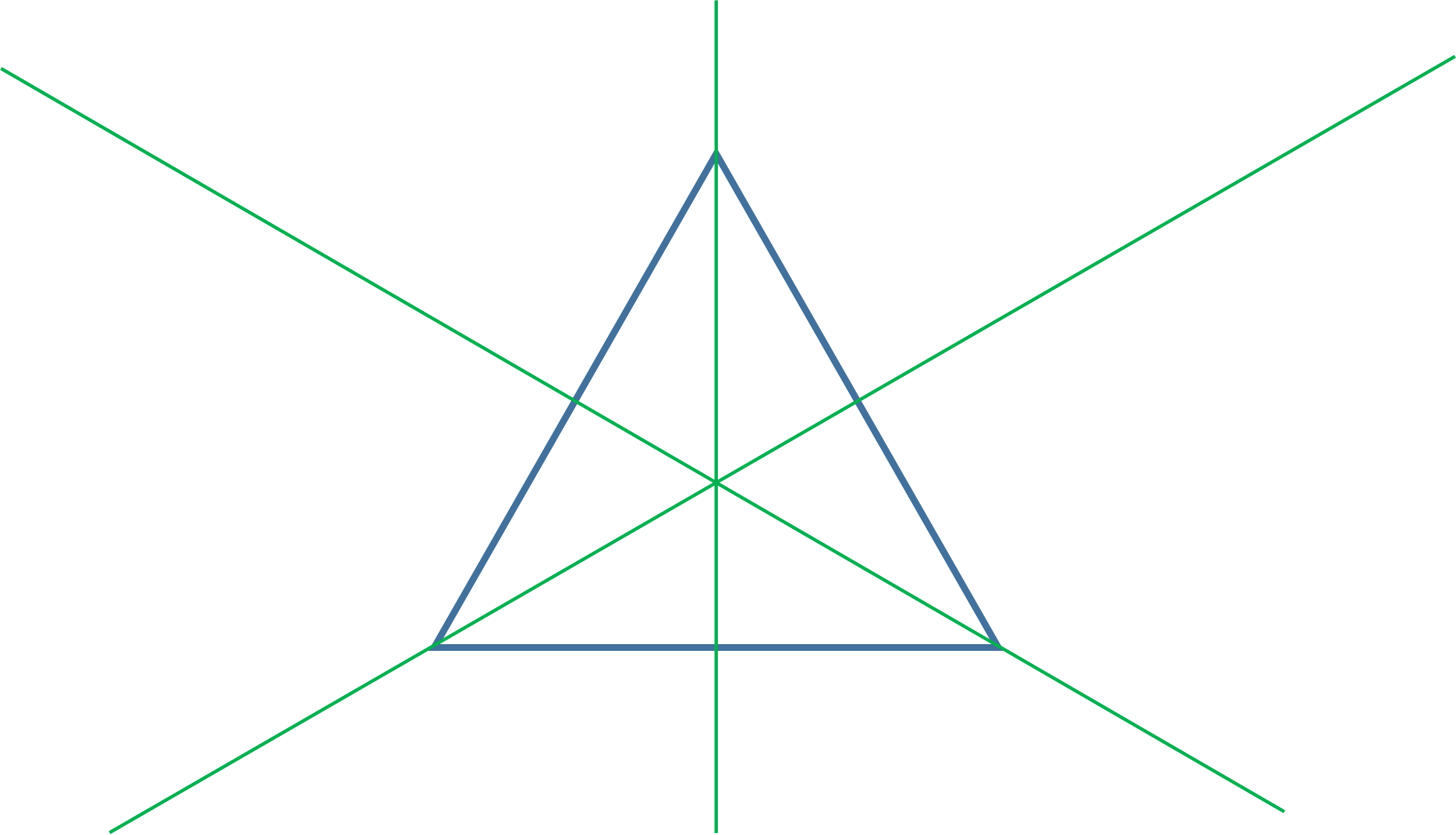
El primero de los polígonos regulares es el triángulo equilátero, en el cual la mediatriz de cada uno de sus lados coincide con la bisectriz de cada uno de sus ángulos. De esta manera se obtienen 3 rectas, que son al mismo tiempo mediatrices, bisectrices y ejes de simetría.
En el cuadrado, las mediatrices y las bisectrices son sólo dos. En este caso, no coinciden.
En el pentágono regular sucede lo que en el triángulo equilátero; cada una de las 5 mediatrices coincide con las bisectrices de los 5 ángulos y son ejes de simetría.
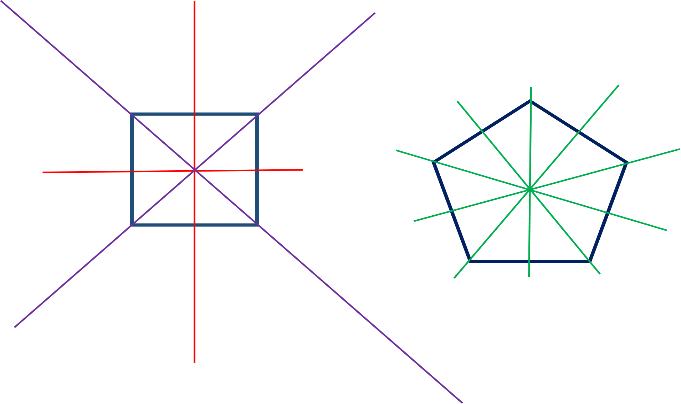
En el hexágono regular son 3 mediatrices y 3 bisectrices. Al igual que en el cuadrado, las rectas no coinciden.
En el heptágono regular son siete mediatrices que coinciden con las siete bisectrices.
Mientras que en el octágono se pueden trazar 4 mediatrices y 4 bisectrices sin coincidir los dos grupos.
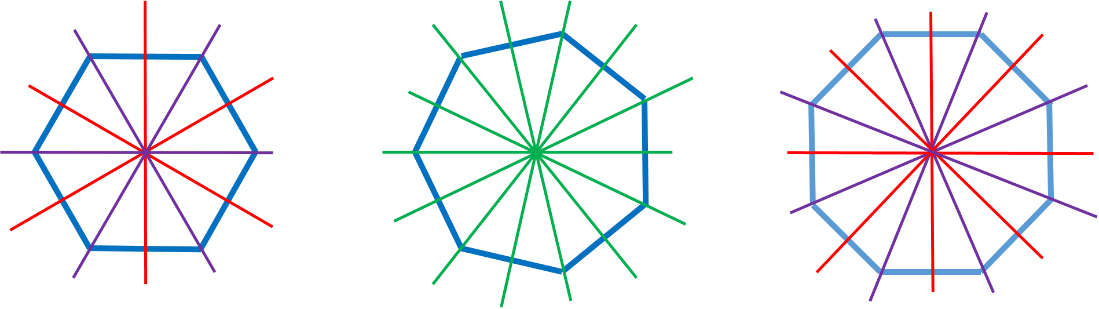
De este modo, se puede identificar un patrón en el número de mediatrices y bisectrices en los polígonos regulares.
Para los polígonos regulares con un número impar de lados, las mediatrices coinciden con el número de bisectrices y con el número de lados, que son las mismas rectas en la figura.
En tanto que, para los polígonos regulares con un número par de lados, el número de mediatrices y de bisectrices que se pueden trazar es igual a la mitad del número de lados, teniendo que para ambos grupos no coinciden.
De esta manera, se puede asegurar que, en un polígono regular de 24 lados, al tener un número par de lados, se pueden trazar 12 mediatrices y 12 bisectrices.
Y para un polígono regular con 17 lados es posible trazar 17 mediatrices y 17 bisectrices.
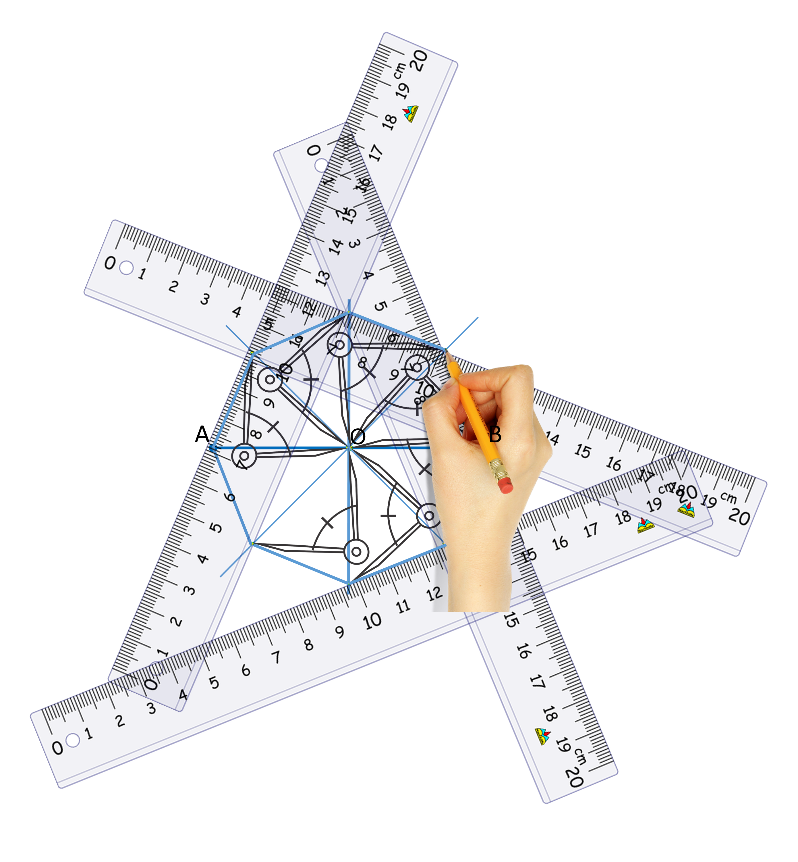
Se pueden retomar las características del octágono regular, que puedes dibujar con un mínimo de trazos porque sólo precisa de una mediatriz y dos bisectrices.
Trázalo, replica los pasos a seguir en tu cuaderno.
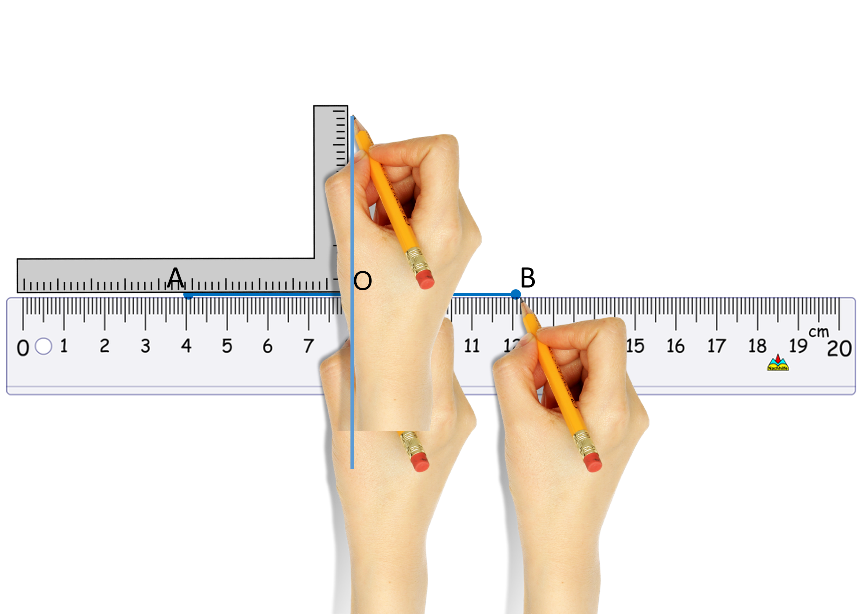
Se traza un segmento de recta AB del tamaño que ocupará todo el octágono.
Se traza la mediatriz de dicho segmento para formar rectas perpendiculares. Se utiliza la regla, se mide el segmento y se determina el punto medio O.
Se utiliza la escuadra y se traza la mediatriz.
Después, manteniendo el compás con la misma abertura, se trazan las dos bisectrices que cortan en dos a los ángulos de 90 grados.
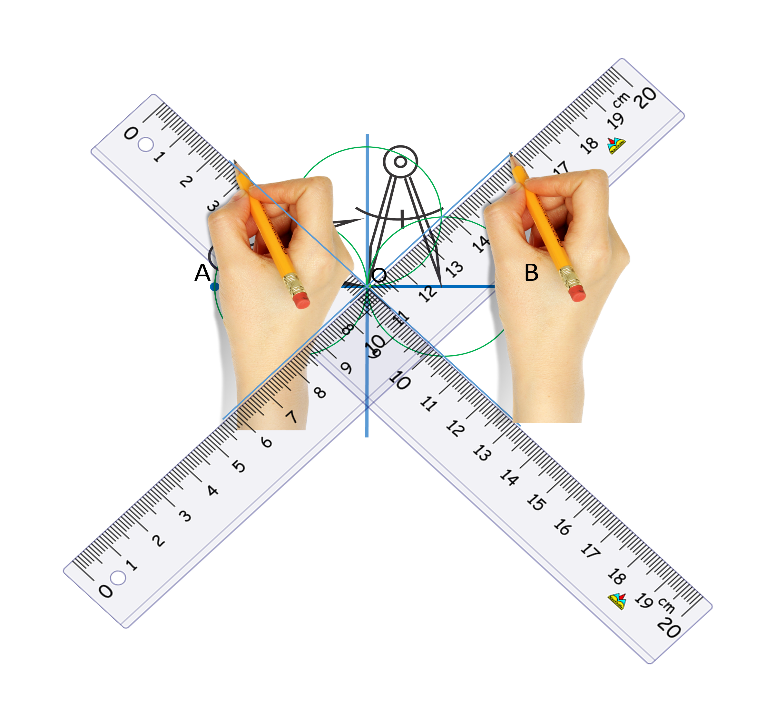
Y, por último, con el compás se hace centro en el punto O y se marca la distancia OB en todas las rectas.
Se tiene como resultado que, al unir todos los puntos, se traza un octágono regular.
Con esta figura regular es posible crear diferentes patrones vistosos y agradables a la vista; por ejemplo:
Cada una de las figuras que se muestran están construidas en su totalidad por octágonos regulares. En algunas ocasiones uno al lado de otro o también sobreponiendo los octágonos para crear diferentes patrones.
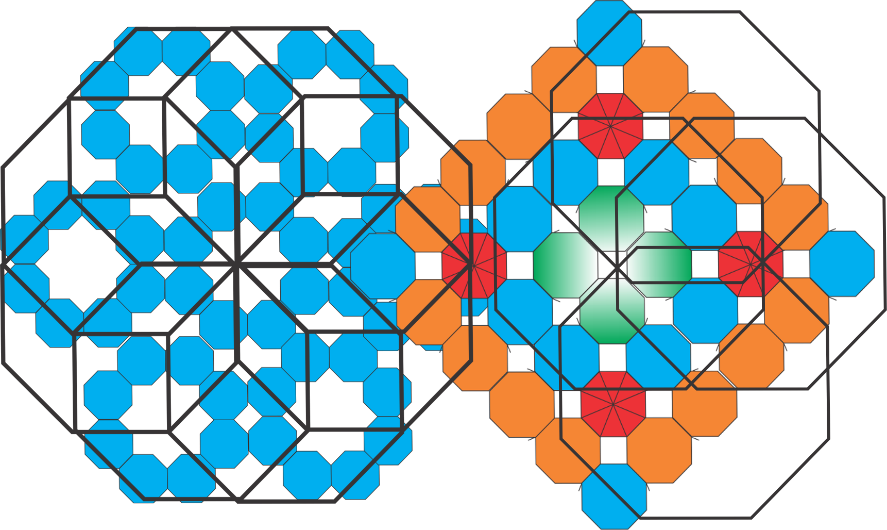
Realiza alguna combinación de formas y colores con los octágonos para practicar la mediatriz y la bisectriz.
Para continuar con el uso de la mediatriz de un segmento y la bisectriz de un ángulo, se construye uno de los sólidos platónicos: el icosaedro, formado por 20 triángulos equiláteros.
Si deseas construirlo necesitas de tu compás, escuadra, un poco de cartón, estambre de color, tijeras, pegamento líquido o pistola de silicón.
Para comenzar, traza en tu cuaderno un cuadrado con la mayor precisión posible; procura cargarlo un poco a la izquierda en la hoja y, de ser posible, que sea similar a la siguiente imagen. Puedes apoyarte de la cuadrícula de las hojas del cuaderno para trazarlo.
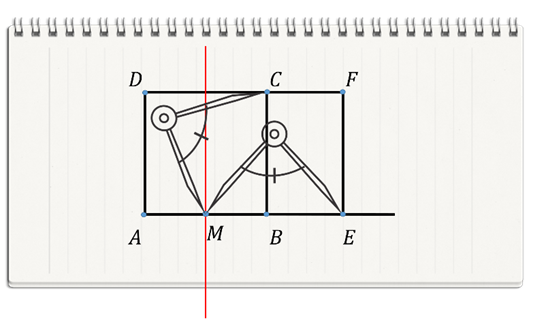
No requiere de ninguna medida en especial, únicamente hacer los trazos con limpieza y precisión.
Para esto, se nombran los vértices del cuadrado como A, B, C, D, en el orden que se muestra en la imagen.
El siguiente elemento que se necesita es el punto medio del segmento AB y aquí se utiliza la mediatriz.
No se necesita trazar la mediatriz, sólo marcar la intersección con el segmento AB, que es el punto medio M.
El siguiente paso es prolongar el segmento AB hacia el lado del punto B:
Se apoya el compás en el punto M y se abre hasta el vértice C para después trasladar esa distancia hasta la prolongación del segmento AB.
A ese punto de intersección se le nombra punto E.
Después se traza una perpendicular al segmento AB que pase por el punto E y se intersecte con la prolongación del segmento DC. A este punto se le nombra punto F.
Con los puntos AEFD se ha creado un rectángulo que suele denominarse rectángulo áureo porque posee una proporcionalidad entre sus lados igual a la razón áurea.
En casa verifica esta proporción, mide la longitud de la base y divídela entre la medida de la altura; el resultado debe ser aproximadamente 1.6180. Lo anterior, sin importar la medida que se haya elegido.
Para continuar, se requiere encontrar el centro de este rectángulo, y se trazan las bisectrices de los ángulos interiores del rectángulo.
Se unen los puntos de intersección de las cuatro bisectrices como se muestra, y se tiene que el punto de intersección de los dos segmentos es el centro del rectángulo.
Para terminar, se apoya el compás al centro del rectángulo, se abre hasta la intersección con el segmento DF y se marcan las intersecciones en el otro segmento.
Se les denominan G y H a los puntos de intersección respectivamente y los unimos con un segmento de recta.
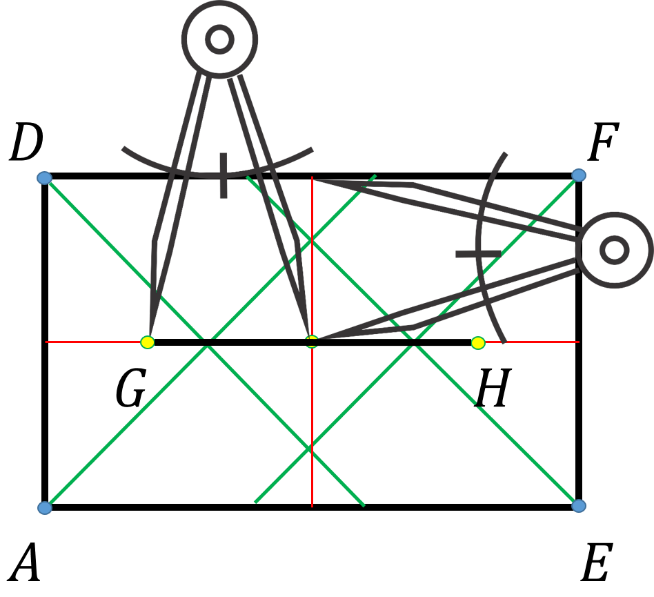
Para la construcción del icosaedro se necesitan tres piezas como la anterior; rectángulos áureos con el segmento GH marcado.
La forma más sencilla de trasladar las medidas al cartón que emplearás es posicionar la hoja con el dibujo sobre el cartón, y sin que ésta se mueva, con la punta del compás se marcan los puntos A, E, F, D, G y H únicamente, el resto de los trazos y puntos fueron auxiliares y ya no se requieren.

Una vez que se marcaron los puntos en el cartón, se recortan los tres rectángulos requeridos.
En dos de ellos recortan el segmento GH, y en el tercer rectángulo se recorta desde el punto G pasando por el punto H y hasta el final de la figura.
Se comienza con la construcción física del icosaedro insertando los dos primeros rectángulos hasta la mitad para insertar, por último, el tercer rectángulo, aprovechando que se extendió el corte hasta el final de la figura.
Una vez en su lugar, se puede usar pegamento para unir el corte extra del último rectángulo.

Para finalizar el icosaedro, se pega el estambre a uno de los vértices de los rectángulos y desde ahí, a cada uno de los 5 vértices a su alrededor. Se repite el procedimiento con todos los vértices, y sin pasar 2 veces por el mismo lugar, hasta terminar la figura.

Se te recomienda buscar un patrón de armado donde tengas que recortar el menor número de veces el estambre.
También se puede reemplazar el estambre por popotes o palillos de madera, que en ambos casos queda bien.
El saber trazar la mediatriz de un segmento y la bisectriz de un ángulo, y conocer bien todas sus propiedades, te permite usarlas como herramientas en un sinfín de procedimientos, cálculos y problemas.
El reto de hoy:
Busca a tu alrededor posibles usos de la mediatriz y la bisectriz, y así practicar el trazo de estas rectas en tu cuaderno.
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto de tercer grado de secundaria, además de compartir los conocimientos a distancia con tus maestras, maestros y compañeros.
¡Buen trabajo!
Gracias por tu esfuerzo.