MCD y mcm
MCD y mcm
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: calcular el MCD y el mcm.
¿Qué vamos a aprender?
A lo largo de la historia el ser humano ha tenido la necesidad de repartir cosas de forma igualitaria, así como de calcular los múltiplos de un número natural.
Trabajarás con divisores y múltiplos. Siempre se ha tenido la necesidad de repartir objetos, entre personas o entre otras cosas, así también el facilitarnos la adición mediante la obtención de productos.
Para iniciar deberás tener presentes los números primos y los criterios de divisibilidad, para después continuar con el significado del mínimo común múltiplo y el máximo común divisor, así como el algoritmo para obtenerlos y aplicarlos para resolver problemas que los involucren.
¿Qué hacemos?
Cuando intentas repartir cantidades de forma igualitaria, has encontrado que no siempre se puede hacer de la mejor forma, que por el número de objetos algunas veces es posible y otras no.
Los griegos tenían una forma muy peculiar de clasificarlos, sumaban los divisores y les restaban el número en cuestión, les llamaban deficientes si la suma era menor, abundantes si la suma era mayor y perfectos si eran iguales.
Existen unos números que se pueden considerar “especiales”: Los números primos, que son aquellos que son divisibles entre sí mismos y la unidad.
Eratóstenes encontró una forma para descubrirlos y hasta la fecha este método se llama “Criba de Eratóstenes”, que es un algoritmo que permite hallar todos los números primos menores que un número natural dado.

También se tiene el famoso teorema de Euclides, quien era un matemático griego, nacido en año 325 antes de nuestra era, que dice que los números primos son infinitos y que todo número se puede descomponer en factores primos.
Más adelante en el tiempo, en el siglo XIX, el matemático, físico y astrónomo alemán Carl Friedrich Gauss encontró un algoritmo para descomponer números en factores primos, llegando de esta forma al mínimo común múltiplo y al máximo común divisor.
Los algoritmos que vas a utilizar provienen de muchos años atrás y siguen estando vigentes.
Con los siguientes números estarás trabajando toda la sesión, así que es importante que los reconozcas primero
Pon atención en la “Criba de Eratóstenes”, los primeros números primos son 2, 3, 5, 7, 11, 13 y 17.
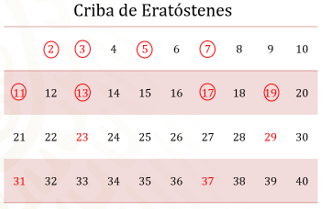
No son los únicos, sin embargo, son los que vas a utilizar. Los números primos son infinitos, al grado que los matemáticos siguen encontrando números primos. El último número encontrado fue en diciembre de 2018 y tiene más de 23 millones de dígitos y todos los días siguen calculando más de ellos.
Ahora, identificarás la divisibilidad como la propiedad de un número entero de poder dividirse por otro, dando como resultado un número entero. Es decir, si un número los divides entre otro y su residuo es cero, implicará que el primero es divisible entre el segundo, si el residuo es diferente de cero, entonces podrás comprender que no es divisible entre ese número.
Existe una forma para conocer que números son divisibles entre otros sin tener que hacer las divisiones.
Hay unas reglas que permiten averiguar rápidamente qué números son divisibles entre otros sin operar el cociente, se llaman criterios de divisibilidad.
Utilizarás los siguientes números 8, 12, 24.
¿Notas alguna regularidad entre ellos?

Si observas con detalle el 8, tiene mitad, el doce también la tiene, la mitad del 24 es doce.
Todos estos números tienen mitad, por lo tanto, son divisibles entre dos, debido a que su último dígito es un número par o cero.
Ahora los siguientes 27, 54, 114, ¿ves alguna regularidad?

Son múltiplos de 3 observa, si sumas los dígitos del 27 ¿cuánto obtienes? 2 más 7 es 9.
Y si sumas los dígitos del 54, es decir, 5 más 4 ¿cuánto da? nueve otra vez. Y si sumas ahora los dígitos de 114: uno más uno más 4, seis. Si observas, todos los números obtenidos son múltiplos de 3, por lo tanto, son divisibles entre 3.
El criterio de divisibilidad del número 5 es que el número termine en cero y 5.

Ya tienes los números primos, los criterios de divisibilidad y ahora, los vas a aplicar para obtener el mínimo común múltiplo conocido como “mcm”, en letras minúsculas y el máximo común divisor conocido como “MCD”, en letras mayúsculas.
Analiza la siguiente situación:
A lo largo de nuestro país hay una gran variedad de tacos, además que son un alimento típico mexicano muy sabroso.
Algunas veces se han encontrado varias veces dos amigos en común comiendo tacos.
Se han visto en una taquería que tiene un gran surtido, incluso han encontrado a otro amigo, Juventino.
La última vez que se vieron en la taquería fue la semana pasada, hace 7 días exactamente, son clientes frecuentes, Alberto va cada 6 días sin fallar, Gerardo cada 8 días y Juventino cada 4 días.
Una pregunta sería ¿cuándo se volverán a encontrar los tres en la taquería?, recuerda que se vieron ahí hace 7 días.
¿Cómo se calcula? Utilizando el mínimo común múltiplo.
Como su nombre lo indica, es el múltiplo que es común a ciertas cantidades y que además es el menor de sus múltiplos comunes.

Utilizarás los días en los cuales cada uno asiste a la taquería y son: 4, 6 y 8.
Inicia con el 4 y cómo estás hablando de múltiplos, el que seguiría es el 8, 12, 16, 20, 24, 28, 32
Y continúas colocando los múltiplos del 4 hasta que consideres que tienes los suficientes.
Haces ahora lo mismo con el número 6, 12, 18, 24, 30, 36.
Ahora con el 8, y son 16, 32, 40, 48
Una vez que has terminado de anotar los múltiplos de cada uno, busca los que son comunes en las tres filas. Observa, primero está el 24 y después el 48.
Solo son dos, pero si continuas encontrarás más múltiplos, pero con los que tienes son suficientes. Por ejemplo, el 24.
El 24 es un múltiplo común y el menor de las tres cantidades.
Entonces este procedimiento es el que debes realizar siempre para obtener el mínimo común múltiplo. Aunque, las listas de múltiplos son fáciles de hacer, pero no siempre es rápido encontrar el múltiplo en común, para eso tienes un algoritmo.
Utiliza el mismo ejemplo, coloca la frecuencia con la que asiste cada uno a la taquería 4, 6 y 8. Traza una línea que te ayude a separar las cantidades y anota los números primos que vas a utilizar, en este caso el 2, el 3 y el 5.

Inicia observando si tus cantidades son divisibles entre el número primo menor que es el 2.
Aplica el criterio de divisibilidad, observa que las tres cantidades terminan en número par, siendo así divisibles entre 2.
Anota el 2 en la parte derecha de la línea, y calcula el cociente de cada uno de los valores y escribe éstos en el renglón inferior.
Analiza los números obtenidos y encuentras que el 4 y el 2 son divisibles entre 2, el cual colocas nuevamente del lado derecho de la línea. Anota ahora en el renglón inferior la mitad de 2 que es 1.
En el caso del 3 no es divisible por lo que lo anotas nuevamente en el siguiente renglón.
Anota también la mitad de 4. Repite el proceso encontrando aún un número divisible entre dos, por lo que vuelves a colocarlo del lado derecho de la línea.
Has terminado con los números divisibles entre dos, selecciona ahora el siguiente número primo, el 3.
Revisa y encuentra que tienes el 3, por lo que lo anotas y realizas la división. El algoritmo termina cuando cada una de las cantidades llega a la unidad.
Como siguiente paso calculas el producto de los números obtenidos del lado derecho de la línea, 2 por 2 por 2 por 3 que da como resultado final 24. Se obtuvo el mismo resultado que en el primer procedimiento. Eso indica que lo has realizado de forma correcta.
Este resultado te ayuda a saber cuándo se van a volver encontrar, pues te indica que siendo constantes en los días que cada uno asiste a la taquería se encontrarán cada 24 días.
Si se vieron hace 7 días entonces se volverán a encontrar los tres en la taquería en exactamente 17 días.
Por cierto, el día que se encontraron Alberto compró 36 tacos de bistec para la familia, Gerardo compró 24 tacos de papa para llevar y Juventino llevó 18 tacos de mole con pollo.
Pero como son amigos decidieron intercambiarlos para que comiéramos de todos los tipos, teniendo la mayor cantidad de tacos posible respetando que compraron diferentes cantidades.
Pero ¿cómo los dividieron? ¿qué procedimiento pueden utilizar?
Existen varias formas, usando porcentajes es una de ellas, pero tendrías que partir los tacos en pedacitos. Así que, se propuso utilizar el máximo común divisor, para conservar el mismo número de tacos, pero ahora surtidos.
¿Qué es el máximo común divisor?
Como su nombre lo indica, es el mayor divisor común a un grupo de cantidades.
Los algoritmos que se usan para el mínimo común múltiplo y el máximo común divisor son muy similares, aunque el concepto es diferente. Toma nota del algoritmo.
Utiliza las cantidades de tacos, es decir, 18, 24 y 36. Como se trata del máximo común divisor ahora en lugar de usar múltiplos debes calcular los divisores de cada número, empieza por el número 18 y tienes que el primer divisor es el 1, después el 2, 3, 6, 9 y el 18.

Por ejemplo, con los del 24, son 1, 2, 3, 4, 6, 8, 12 y 24.
Lo mismo se aplica para el 36, empieza por el número uno y anótalos en orden hasta llegar al mismo 36, deben estar todos, si te equivocas puedes correr el riesgo de no encontrar la respuesta correcta.
Ahora busca los comunes en las tres filas de números, empieza por el 1. Cabe resaltar que es el divisor de todos los números.
El 2 también está en los 3 renglones. El 3 también coincide y el 6, todos son comunes. Ahora, como el concepto dice que es el mayor de los divisores ¿cuál es el número más grande? El 6
Encuentras que el máximo común divisor de 18, 24 y 36 es 6.
Al igual que en el mínimo común múltiplo ¿existe algún procedimiento formal?
Existe un algoritmo formal para poder obtenerlo y que en el caso de cantidades muy grandes facilita sus cálculos.
El algoritmo para usar es el mismo que usas para el mínimo común múltiplo, con algunas variantes.
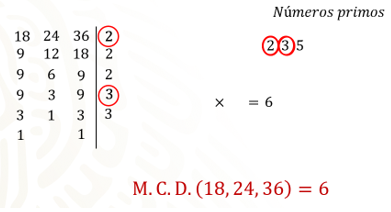
Utiliza los números 18, 24 y 36. Traza una línea que ayuda a separar las cantidades y ahora los números primos que vas a utilizar, en este caso el 2, el 3 y el 5.
Empieza a buscar divisibles con el número primo más pequeño, el 2.
Observa que las tres cantidades terminan en número par, por lo tanto, son divisibles entre 2 y anotas los resultados, además marcas este dos, porque dividió a las 3 cantidades.
Analiza los siguientes números y encuentras que el 9 no es divisible entre 2, pero el 12 y el 18 son pares; anotas otro 2 en la parte derecha de la línea; repite el 9 y escribe el resultado de dividir 12 y 18, es decir 6 y 9.
Repite el proceso, encuentras que el 6 es divisible entre dos, colocas el 2 del lado derecho de la línea.
Anota en el siguiente renglón el 9, la mitad de 6, que es 3 y el otro 9 obtenido.
Has terminado con los números divisibles entre dos, utiliza ahora el siguiente número primo, el 3.
Analiza y todos son divisibles entre 3, anota el 3 en el lado derecho de la línea y el resultado de los cocientes en el siguiente renglón, marca este número porque dividió las tres cantidades.
Sólo falta un 3, lo divides entre 3 y por fin llegas a tener todas las cantidades en 1.
La variante con el proceso anterior es que multiplicarás únicamente aquellos números primos que dividieron exactamente a las 3 cantidades, ¿recuerdas los números que marcaste?
Los multiplicas y el resultado del producto es 6.
Entonces el máximo común divisor de 18, 24 y 36 es 6. Y nuevamente obtuviste el mismo resultado.
Analiza cómo se repartieron los tacos. Como el 6 es el máximo común divisor, cada uno de ellos dividió sus tacos en grupos de 6 y quedaron exactos, de ahí la importancia de usar este algoritmo.
Cada uno compró diferentes cantidades de tacos y se respetó eso. Esta distribución no es equitativa, lo importante es repartir lo más proporcionalmente posible de acuerdo con la cantidad de tacos que cada uno compró y que todos al menos tuviéramos un grupo de los tres diferentes tipos de tacos.
Inicialmente Alberto tenía 6 grupos de tacos, Gerardo tenía 4 y Juventino tres.
Así que sólo se intercambiaron los grupos de 6 de tacos. Alberto se llevó 3 grupos de 6 tacos de bistec, porque fue quién más compró, compartió dos con Gerardo, ya que en cantidad numérica es el que sigue y uno con Juventino, porque fue el que menos compró.
Gerardo compartió dos grupos de seis tacos de papa con Alberto, porque es quien compró el mayor número de tacos, y entregó un grupo a Juventino.
Y Juventino repartió un grupo de tacos de mole con pollo a cada uno de ellos.
Si observas bien la imagen, al final del intercambio cada uno conservó la cantidad de tacos que compró.
Así que dentro de 17 días se volverán a encontrar.
El reto de hoy:
Recuerda exponer tus dudas y comentarios a tus docentes y compartir lo aprendido con tus compañeras y compañeros en la medida de lo posible.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas