Las ecuaciones
Las ecuaciones
Aprendizaje Esperado: consolida contenidos del eje: número, álgebra y variación.
Énfasis: integrar contenidos del tema: ecuaciones.
¿Qué vamos a aprender?
En esta sesión concluirás el estudio de las ecuaciones.
Ten a la mano tu cuaderno o algunas hojas de papel, lápiz, goma, sacapuntas y bolígrafo para hacer tus anotaciones. Así como tu libro de texto.
¿Qué vamos a hacer?
Para iniciar esta sesión, se resolverá el siguiente problema.

En casa estima un número que consideres la solución del problema. ¿El número será entero o fraccionario? ¿Será positivo o negativo?
Reflexiona un poco acerca de este problema, ¿tú puedes resolver el problema inmediatamente? ¿A qué puedes recurrir para encontrar la solución de este problema?
Puedes plantear una ecuación y resolverla.
Para plantear la ecuación debes definir cuál es la literal que vas a utilizar y lo que ésta representa. En este caso se elegirá a la letra “z” para representar al número desconocido y poder plantear la ecuación.
Hay que ir construyendo la ecuación. El triple de un número se representa como 3 “z”; aumentado en 6, se escribe más 6; es igual al simétrico de ese número, pones igual a “z” negativo, y finalmente, disminuido en 10, anotas menos 10. Quedando la ecuación 3 “z” más 6 igual a “z” negativo menos 10.

Reflexiona acerca de lo que se ha planteado. ¿Cuántas ecuaciones se requieren para resolver este problema? ¿Cuántas incógnitas tiene? ¿Qué tipo de ecuación se plantea?
Puedes notar que se ha planteado una sola ecuación que representa al problema, 3 “z” más 6 igual a “z” negativo menos 10. También puedes advertir que únicamente tienes una incógnita, que es “z”, y que la ecuación es lineal o de primer grado, ya que el exponente mayor que se encuentra en la literal es uno y esto determina el grado de una ecuación.
¿Recuerdas cómo puedes resolver esta ecuación?
Un camino cuando comienzas en el estudio del álgebra involucra el ensayo y error, es decir, propones un número como el valor de “z”, lo sustituyes en ambos miembros de la ecuación, resuelves las operaciones y verificas que se cumpla la igualdad.
Sin embargo, este procedimiento te puede llevar mucho tiempo y como ya conoces algunas propiedades de las ecuaciones, puedes utilizarlas para obtener el valor de “z”.
Hay que resolver la ecuación.
Tienes 3 “z” más 6 igual a “z” negativo menos 10. Sumas “z” en ambos miembros de la igualdad y obtienes 3 “z” más “z”, más 6 igual a “z” negativo más “z” menos 10.
Al simplificar los términos semejantes, tienes que 3 “z” más “z” es 4 “z”, más 6 que ya estaba, es igual a “z” negativo más “z” que es igual a cero menos 10.
Como cero menos 10 es igual a 10 negativo, te queda la ecuación 4 “z” más 6 igual a 10 negativo.
Piensa ahora, ¿qué tipo de número debe ser “z”, para que al multiplicarse por 4 y sumarle 6 se obtenga 10 negativo?
Seguramente ya te disté cuenta que debe ser un número negativo, pero ¿cuál es ese número?
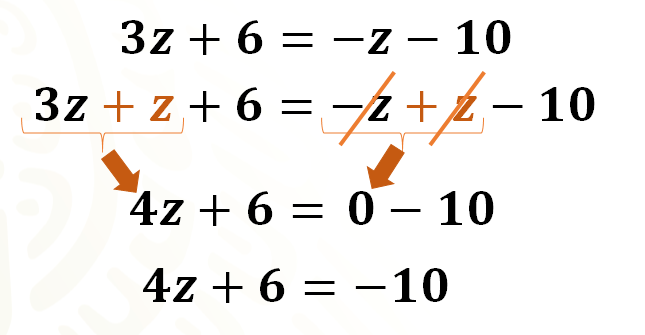
Se continúa despejando “z”.
¿Qué procedimiento se puede seguir para determinar el valor de “z”?
Puedes restar 6 en ambos miembros de la ecuación y la igualdad se conserva.
De esta manera, se tiene 4 “z” más 6 menos 6 igual a 10 negativo menos 6. Al resolver las operaciones, te queda 4 “z” igual a 16 negativo. En este momento piensa en un número tal que al multiplicarlo por 4 se obtenga 16 negativo.
Seguramente ya sabes cuál es el valor de “z”, sin embargo, hay que seguir despejando la incógnita. Para ello, se divide ambos miembros de la ecuación entre 4.
Así tienes 4 “z” entre 4 igual a 16 negativo entre 4. Al resolver las operaciones obtienes “z” igual a 4 negativo.
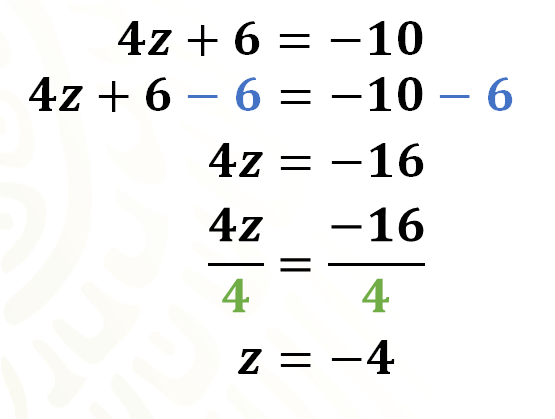
¿Coincidió este valor con tu estimación inicial?
Ahora, debes corroborar que la solución de la ecuación es “z” igual a 4 negativo.
Recuerda que, para realizar la comprobación, se sustituye el valor obtenido de “z” en la ecuación que se planteó originalmente, es decir, 3 “z” más 6 igual a “z” negativo menos 10.
¿Será igual 3 por 4 negativo más 6 que el simétrico de 4 negativo menos 10?
Al resolver las operaciones respetando la jerarquía de operaciones se tiene que, en el primer miembro de la igualdad, 3 por 4 negativo es 12 negativo, más 6 son 6 negativo.
En el segundo miembro de la igualdad tienes que el simétrico de 4 negativo es 4 positivo menos 10 resulta 6 negativo. Como en ambos miembros de la ecuación se obtiene el mismo valor numérico, 6 negativo, se puede afirmar que se cumple con la igualdad, por lo tanto, se puede decir que “z” satisface la ecuación y con ello se resuelve el problema.

Se ha resuelto un problema mediante el planteamiento de una ecuación lineal con una incógnita.
Analiza otro problema y reflexiona en torno al tipo de ecuaciones que te ayudan a resolverlo.

La suma de dos números es 6 y su diferencia es 10 negativo. ¿Cuáles son esos números?
Reflexiona, ¿cuántas incógnitas tiene el problema? ¿Cuántas ecuaciones se pueden plantear para resolverlo? ¿El problema tiene solución?
Anota tus reflexiones y tus estimaciones en tu cuaderno.
Identifica que hay dos incógnitas a las que se les llamará “x” y “y”, donde “x” representa al primer número desconocido y “y”, al segundo.
Al analizar el enunciado del problema, puedes identificar que está formado por dos partes. La primera se refiere a que la suma de dos números es igual a 6, es decir “x” más “y” igual a 6, mientras que la segunda parte se refiere a la diferencia entre estos números desconocidos, es decir, “x” menos “y” igual a 10 negativo.
Te puedes dar cuenta que tienes 2 ecuaciones lineales con 2 incógnitas.
Para que el sistema tenga solución, el valor numérico de “x” en ambas ecuaciones debe ser el mismo.
De la misma forma, el valor numérico de “y” en ambas ecuaciones debe ser el mismo.

Analiza cómo puedes resolver este sistema de dos ecuaciones lineales con dos incógnitas.
Puedes resolver el sistema sumando ambas ecuaciones, recordando que se suman los términos semejantes.
“X” más “x” es igual a 2 “x”, y “y” más su simétrico es cero, igual a, 6 más 10 negativo igual a 4 negativo, quedando 2 “x” igual a 4 negativo. Para despejar “x” se dividen ambos miembros de la igualdad entre 2 y se obtiene que la mitad de 2 “x” es “x” y la mitad de 4 negativo es 2 negativo.
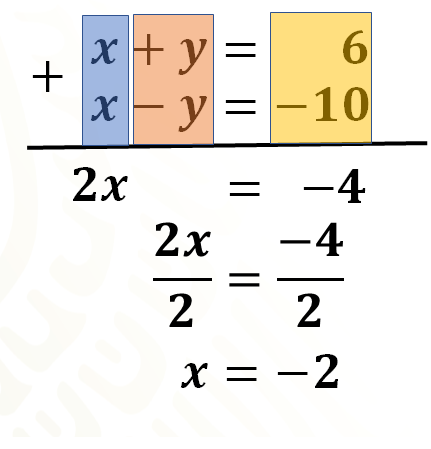
Has encontrado al primer número desconocido. Ahora, ¿qué haces para encontrar el segundo número desconocido, ósea, el valor de “y”?
Seguramente recuerdas que, para encontrar el valor de “y”, se sustituye el valor de “x” igual a 2 negativo en cualquiera de las ecuaciones originales que se plantearon.
Hay que obtener el valor numérico de “y” de la ecuación “x” más “y” igual a 6. Al sustituir, tienes 2 negativo más “y” es igual a 6. Para despejar “y” sumas el simétrico de 2 negativo, que es 2 positivo, en ambos miembros de la igualdad y la igualdad se conserva, quedando 2 negativo más 2 más “y” igual a 6 más 2.
Resolviendo las operaciones se obtiene que “y” es igual a 8.
Ahora, debes realizar la comprobación en ambas ecuaciones, para saber si cuando “x” es igual a 2 negativo y “y” es igual a 8 se satisfacen ambas ecuaciones.
Al sustituir los valores anteriores en la ecuación “x” más “y” igual 6 tienes, 2 negativo más 8 igual a 6. Al resolver las operaciones en el primer miembro de la ecuación obtienes 6, recuerda que esto es en el primer miembro y al compararlo con el segundo miembro observas que ambos valores numéricos son iguales.
Ahora, al sustituir los valores de “x” y de “y” para comprobar en la ecuación “x” menos “y” igual a 10 negativo, tienes que, 2 negativo menos 8 debe resultar 10 negativo.
Al resolver la operación en el primer miembro de la igualdad tienes que, si a 2 negativo le restas 8 obtienes 10 negativo y al compararlo con el segundo miembro de la igualdad, que es 10 negativo, te puedes percatar que se cumple la igualdad, por lo tanto, se puede afirmar que la solución del sistema se cumple cuando “x” es igual a 2 negativo y “y” igual a 8.

Una forma de visualizar la solución de cualquier sistema de ecuaciones es trazando las gráficas de ambas ecuaciones en un mismo plano cartesiano.
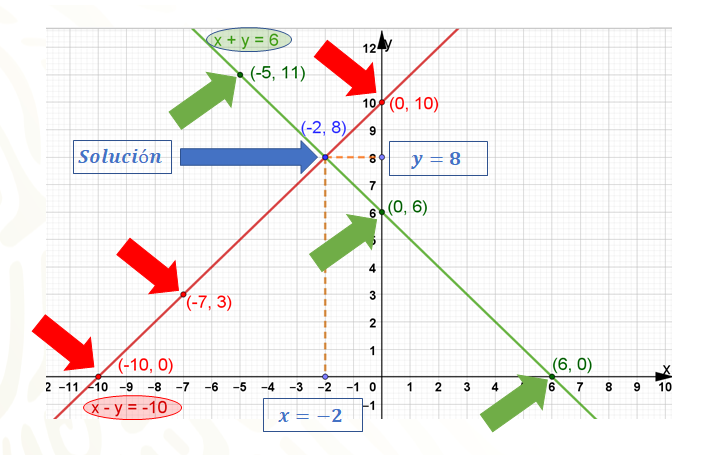
Observa este sistema de ecuaciones trazado en un plano cartesiano. Analiza la ecuación “x” más “y” igual a 6. Todos los puntos que pertenecen al segmento de recta en color verde deben cumplir que su suma sea 6. Por ejemplo, para el punto 5 negativo coma 11, al sumarse estos valores se obtiene 6; de la misma forma, para el punto cero coma 6, así como también el punto 6 coma cero, o cualquier otro punto que pase por esa recta, se cumple que el valor de “x” más el valor de “y” es igual a 6.
De manera análoga, revisa la ecuación “x” menos “y” igual a 10 negativo donde se representa una parte de su gráfica por el segmento de recta en color rojo. Puedes darte cuenta de que el punto en donde “x” es igual a cero y “y” es igual a 10, cero menos 10 es igual a 10 negativo.
Por otro lado, el punto en donde “x” es igual a 7 negativo y “y” igual a 3, al restar 3 a 7 negativo, también se obtiene 10 negativo. Si analizas el punto donde “x” es igual a 10 negativo y “y” igual a cero, al restarle cero a 10 negativo, tienes 10 negativo. Si analizas cualquier otro punto de esa recta, y restas al valor de “x” el de “y” siempre vas a obtener 10 negativo.
Reflexiona. ¿Existe un punto en el cual en ambas ecuaciones tienen la misma coordenada? Es decir, ¿hay un valor de “x” y un valor de “y” tal que satisfaga ambas ecuaciones?
En este caso ¡sí lo hay! Es el punto de intersección de los dos segmentos de recta que se muestran en la imagen, donde “x” es igual a 2 negativo y “y” es igual a 8, que corresponde a la solución que se había encontrado cuando se resolvió el sistema sumando las ecuaciones.
Pero, te has preguntado si hay sistemas de ecuaciones lineales que no tengan solución o que tengan un número infinito de soluciones, ¿cómo te puedes dar cuenta de esto? Ve pensando en esto mientras se revisa el tercer problema.

Respecto de la primera pregunta, se puede decir que se está preguntando por 2 números. En este caso, se representarán con las letras “x” y “y”, donde “x” representa al primer número desconocido y “y” representa al segundo número.
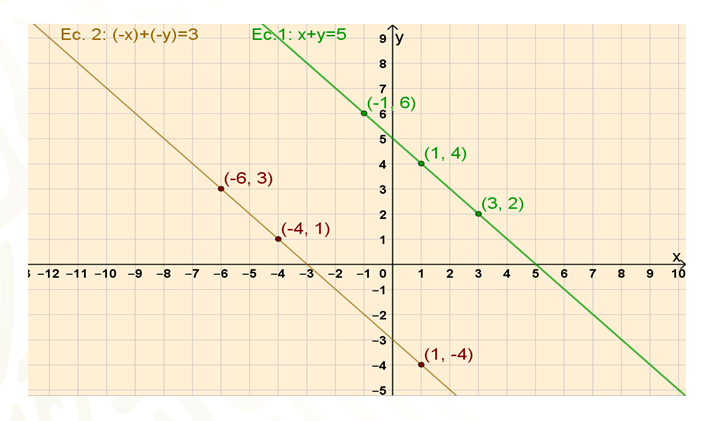
Al analizar el problema se identifica en la primera parte del enunciado que la suma de los números, es decir, “x” más “y” es igual a 5, entonces tienes la ecuación “x” más “y” igual a 5.
En la segunda parte del enunciado se indica que la suma de los simétricos de esos números, es decir, el simétrico de “x” más el simétrico de “y” es igual a 3, obteniendo la ecuación “x” negativa más “y” negativa igual a 3.

Como puedes darte cuenta, se ha planteado un sistema de dos ecuaciones lineales con dos incógnitas que representan al problema. Debes recordar que cuando se trata de un sistema de ecuaciones, ambas ecuaciones deben satisfacerse simultáneamente para que el sistema tenga solución.
Antes de seguir analizando las ecuaciones que se plantearon, ¿recuerdas cómo se determina la solución de un sistema de dos ecuaciones lineales con dos incógnitas cuando se representan en un plano cartesiano?
La solución de un sistema de ecuaciones se obtiene gráficamente cuando éstas se cruzan, es decir, en la intersección de las ecuaciones, como lo pudiste observar en la resolución del problema anterior.
Una vez que has recordado esto, se puede continuar con el análisis de este sistema que representa al tercer problema.
Esta vez se iniciará con el método gráfico.
Se despeja “y” en ambas ecuaciones.
Para despejar “y” de la ecuación 1, “x” más “y” igual a 5, restas “x” en ambos miembros de la igualdad. Al simplificar términos semejantes tienes que “y” es igual a 5 menos “x”. De manera análoga, para despejar “y” en la ecuación 2, primero sumas “x” en ambos miembros de la igualdad, obteniendo el simétrico de “y” igual a 3 más “x”. Luego multiplicas ambos miembros de la igualdad por 1 negativo, quedando, “y” igual al simétrico de “x” menos 3.

Ahora se darán tres valores a “x”, se determinarán los de “y” para cada ecuación y se trazarán las gráficas de las ecuaciones.
Para la ecuación 1.
Si “x” es igual a 1 negativo, “y” es igual a 5 menos 1 negativo igual a 6.
Si “x” es igual a 1, “y” es igual a 5 menos 1, igual a 4.
Si “x” es igual a 3, “y” es igual a 5 menos 3, igual a 2.
La recta que pasa por esos puntos corresponde a la ecuación “x” más “y” igual a 5.
Para la ecuación 2.
Si “x” es igual a 6 negativo, “y” es igual al simétrico de 6 negativo que es 6, menos 3, igual a 3.
Si “x” es igual a 4 negativo, “y” es igual al simétrico de 4 negativo que es 4, menos 3, igual a 1.
Si “x” es igual a 1, “y” es igual al simétrico de 1 que es 1 negativo, menos 3, igual a 4 negativo.
La recta que pasa por esos puntos corresponde a la ecuación el simétrico de “x” más el simétrico de “y” es igual a 3.
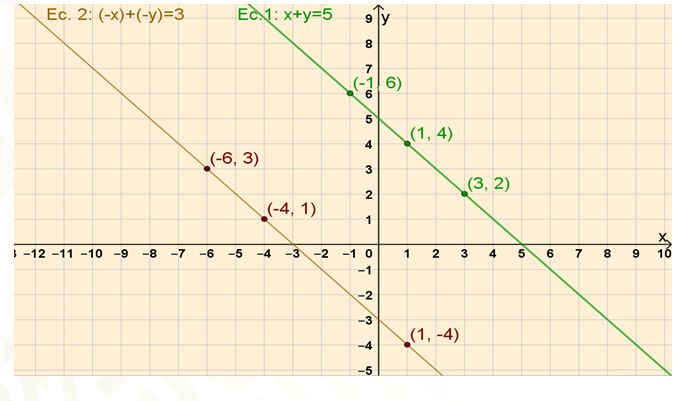
Analiza las gráficas y contesta, ¿existe algún punto en común que satisfaga a ambas ecuaciones? En otras palabras, ¿las ecuaciones se cruzan en algún punto?
Las ecuaciones no se cruzan en ningún punto en la sección del plano que se está analizando, por lo tanto, no se puede afirmar aún si tienen o no solución, ya que como sabes, lo que se muestra aquí son sólo segmentos de las rectas que representan ambas ecuaciones, y estas rectas se extienden de manera indefinida en ambas direcciones, por lo tanto, no se sabe si se cruzarán al extenderlas. Por lo tanto, se usará otro método para averiguar si el sistema de ecuaciones tiene o no tiene solución.
Si se igualan los despejes de “y” en la ecuación 1 con el de “y en la ecuación 2, se obtiene que: 5 menos “x” es igual a “x” negativa menos 3. Al sumar “x” en ambos miembros de la igualdad y simplificar términos semejantes, se obtiene una inconsistencia ya que 5 no es igual a 3 negativo, esto quiere decir que el sistema es inconsistente y que no tiene solución.

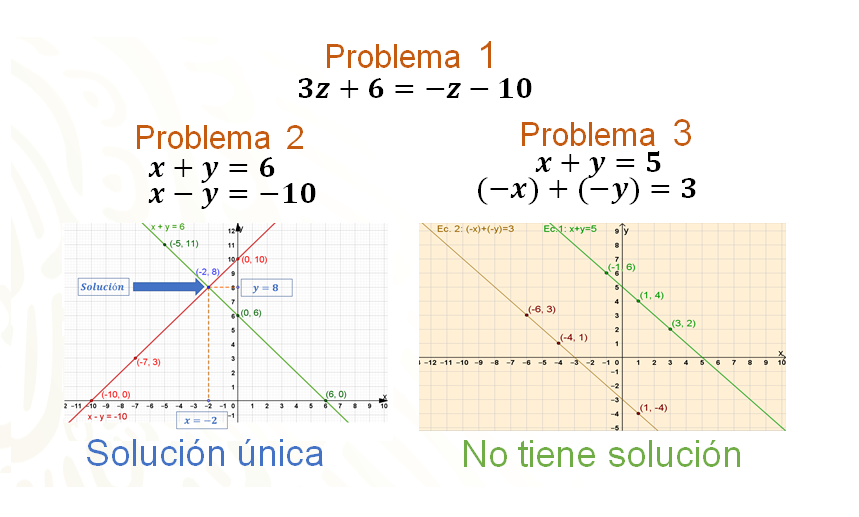
Ahora se realizará una pausa y analiza lo siguiente. ¿Qué tipo de ecuaciones se han utilizado para resolver los problemas y qué tipo de solución tienen?
En el primer problema se planteó una ecuación lineal con una incógnita que tiene una solución. En el segundo problema se planteó un sistema de dos ecuaciones lineales con dos incógnitas que tiene solución única. En el tercer problema se planteó un sistema de dos ecuaciones lineales con dos incógnitas que no tiene solución.
Ve realizando tus anotaciones de cómo puedes identificar cuándo un sistema de ecuaciones tiene solución única y cuándo no tiene solución. Piensa si estos son los únicos tipos de solución que se pueden presentar cuando tienes sistemas de ecuaciones.
Hay que resolver el cuarto y último problema de esta sesión.

El problema tiene dos incógnitas que son los números desconocidos a los que se le asignarán las literales. “X” representa al primer número desconocido y “y” representa al segundo número desconocido.
Al analizar el enunciado del problema, en la primera parte se indica que el triple de un número, es decir, 3 “x” es igual al doble del segundo número, esto es 2 “y”, quedando la ecuación 3 “x” igual a 2 “y”. Luego, se indica que el segundo número “y” es igual a 1 punto 5 veces “x”, es decir “y” igual a 1 punto 5 “x”, que es una segunda ecuación. Entonces, tienes 2 ecuaciones lineales con 2 incógnitas lo que representan un sistema de ecuaciones.

Ahora, se debe determinar si este sistema tiene solución o no, y si tiene solución ¿cuál es?
Con lo que has estudiado hasta este momento, ¿Cómo puedes darte cuenta si este sistema tiene o no solución?
Una forma de identificar cuándo un sistema tiene solución es trazando sus gráficas en el plano cartesiano y, si éstas se intersecan o se cruzan en un sólo punto, quiere decir que el sistema tiene solución única. Pero esto no ocurre siempre ya que, si, al trazar las gráficas, éstas nunca se intersecan, quiere decir que el sistema es inconsistente y que no tiene solución.
¿Qué piensas de este nuevo sistema de ecuaciones? ¿Tiene solución única o no tiene solución?
Hay que tratar de resolver el sistema por el método gráfico y se verá qué es lo que sucede.
¿Recuerdas el procedimiento?
Para la ecuación 1 despejas “y”, y así obtienes que “y” es igual a 3 “x” entre 2.
Se dan algunos valores a “x” y calculas el valor de “y” para esta ecuación, con lo que se determinan las coordenadas. Así, si “x” es igual a cero entonces, “y” es igual a cero y si “x” es igual a 2, “y” es igual a 3. Con estos puntos trazas la gráfica de la ecuación 1, de color rojo.
Para la ecuación 2 tienes que “y” es igual a 1 punto 5 “x”.
Se dan algunos valores a “x” y calculas el valor de “y” para esta ecuación, con lo que se determinan las coordenadas.
Así, si “x” es igual a 4 entonces, “y” es igual a 6 y si “x” es igual a 6, “y” es igual a 9. Con estos puntos se traza la gráfica de la ecuación 2, de color verde.
¿En cuántos puntos se intersecan las ecuaciones? ¿Cuántas soluciones tiene el sistema de ecuaciones?
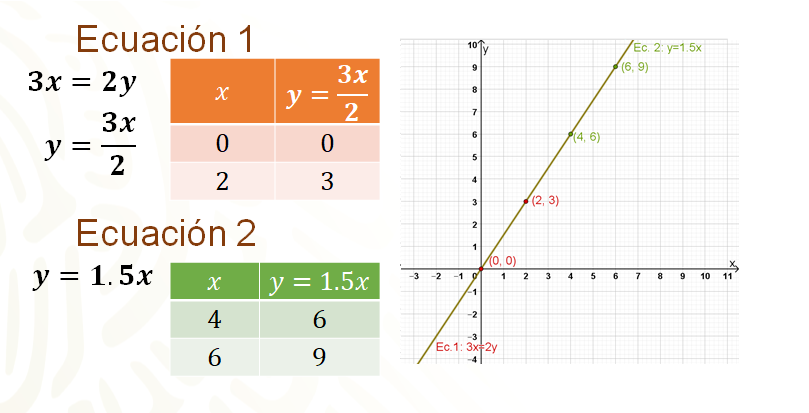
Seguramente ya te disté cuenta que al trazar ambas ecuaciones estas coinciden en todos sus puntos, esto quiere decir que hay un número infinito de soluciones. Esto sucede cuando las ecuaciones son dependientes entre sí.
Compara ambas ecuaciones y determina por qué en este sistema las ecuaciones son dependientes.
Has analizado casos de sistemas de dos ecuaciones lineales con dos incógnitas, cuando un sistema tiene solución única, cuando no tiene solución y cuando tiene un número infinito de soluciones.
Con esto, has llegado al final de esta sesión. Recuerda que para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de Matemáticas de Segundo Grado y otras fuentes confiables. De igual manera puedes recurrir a tu profesora o profesor de esta asignatura.
El reto de hoy:
En tu cuaderno realiza un mapa conceptual, en el que presentes los sistemas de ecuaciones que incluyan un ejemplo con solución única, otro con un número infinito de soluciones y un tercero que no tenga solución.
Asimismo, concluye los ejercicios que se efectuaron en el desarrollo de la sesión, en caso de que aún te falte realizarlos o terminarlos.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas