La proporcionalidad
La proporcionalidad
Aprendizaje esperado: consolida contenidos del eje: número, álgebra y variación.
Énfasis: integrar contenidos del tema: proporcionalidad.
¿Qué vamos a aprender?
En esta sesión recuperarás aprendizajes del contenido de proporcionalidad, tanto directa como inversa.
¿Qué hacemos?
En sesiones anteriores trabajaste contenidos de proporcionalidad directa y proporcionalidad inversa; en esta sesión harás una remembranza de sus aspectos conceptuales y procedimentales.
En tu vida diaria, ¿has escuchado la palabra proporcionalidad? O tal vez cuando dicen, estas cantidades son proporcionales, o quizá no de manera explícita, sin embargo, este concepto está implícito en situaciones como todos los productos de limpieza al 3 por 2, o al calcular la cantidad de ingredientes de un postre para un determinado número de personas. Estas son sólo algunas de muchas situaciones donde se hace uso de la proporcionalidad.
Para continuar, recuperarás los conceptos de razón y de proporción.
Una razón es un vínculo entre dos cantidades que se pueden comparar. Si dos o más razones tienen el mismo valor, entonces son proporcionales. De tal manera que una proporción es la igualdad de dos razones del mismo valor; una razón se puede escribir como una fracción.
Analiza la siguiente situación.
En el establecimiento “@rrob@”, 3 memorias USB tienen un costo de $ 336 pesos, en tanto que en el negocio “Infinito”, 8 de esas memorias cuestan $ 896 pesos.
- Expresa cada relación como una razón
- Determina si esas razones forman una proporción
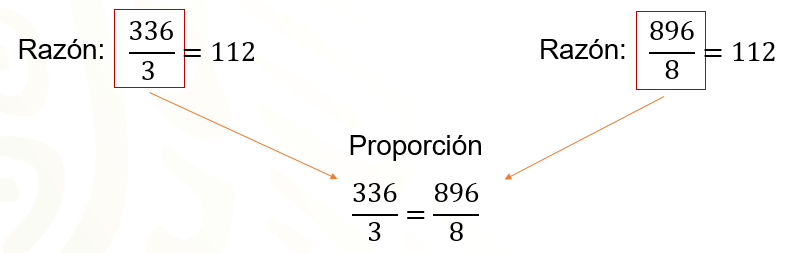
La razón para el establecimiento “arroba” entre el costo que se paga por las memorias y el número de memorias es 336 es a 3; si se halla el valor correspondiente se obtiene 112; y para el negocio “Infinito” la razón es 896 es a 8, con valor igual a 112.

Esto significa que, en ambos negocios, el precio unitario de esas memorias es de 112 pesos.
El valor en ambas razones es 112, por lo tanto, podemos afirmar que esas razones forman una proporción, que es 336 es a 3 como 896 es a 8. Esta proporción se puede escribir como la igualdad de fracciones 336 entre 3 igual a 896 entre 8.
Ahora, recupera los criterios para determinar cuándo las magnitudes tienen una relación de proporcionalidad directa o inversa. Para ello, realiza la siguiente actividad.
Se muestran cuatro tablas. Identifica si las tablas contienen magnitudes en una relación de proporcionalidad directa, inversa o ninguna de las dos.
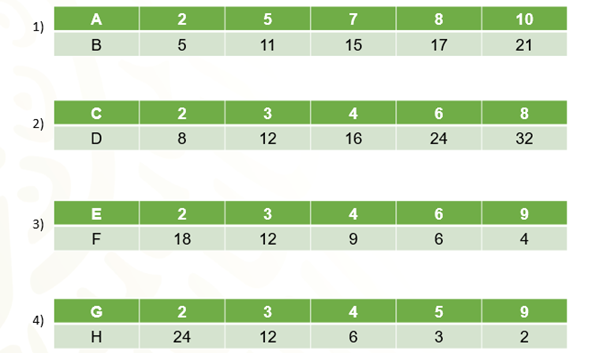
¿Qué criterios utilizarías para saber cuándo dos magnitudes varían de manera proporcional directa o inversa?
Dos magnitudes son directamente proporcionales si…
- Al aumentar o disminuir una de sus magnitudes, la otra aumenta o disminuye respectivamente en la misma proporción.
- El cociente entre los valores correspondientes de cada una de las magnitudes es constante, es decir, “k” es igual a “y” entre “x”.
Dos magnitudes son inversamente proporcionales si…
- Al aumentar una de las magnitudes, la otra disminuye en la misma proporción, y si una disminuye, la otra aumenta en la misma proporción.
- El producto entre las magnitudes de sus valores correspondientes es un valor constante, es decir, “x” por “y” es igual a “k”.
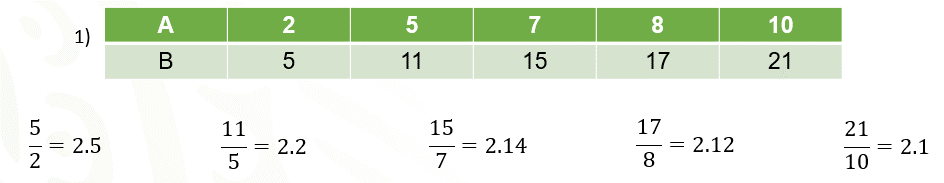
En la tabla 1, los valores de ambas magnitudes aumentan. Si calculamos los cocientes de los valores de las magnitudes que se corresponden, nos damos cuenta que no son iguales, esto quiere decir que dichos valores no son proporcionales.
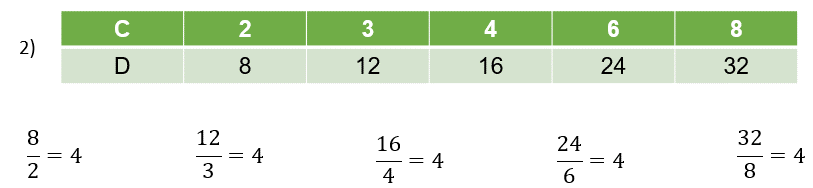
Para la tabla 2, al aumentar los valores de una magnitud los de la otra también aumentan. En este caso, todas las divisiones tienen cociente igual a 4, por lo tanto, esto significa que esta es una relación de proporcionalidad directa.
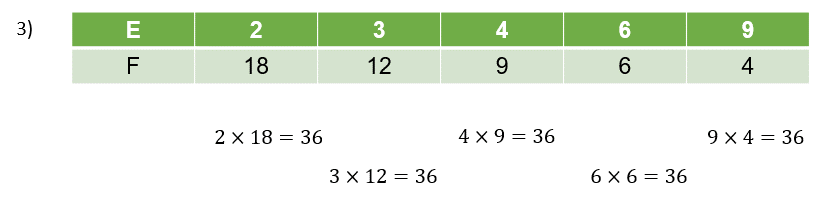
En la tabla 3, al aumentar los valores de una magnitud, los de la otra, disminuyen. El producto de las magnitudes correspondientes es 36, es decir, una constante, lo que significa que es una relación de proporcionalidad inversa.
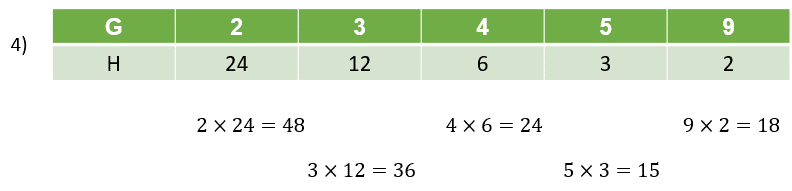
Para la tabla 4, aunque al aumentar una de las magnitudes la otra disminuya, no son magnitudes inversamente proporcionales, ya que los productos entre los valores respectivos no son constantes.
Con esta actividad se mostró cómo se puede determinar cuándo una relación entre dos magnitudes es de proporcionalidad, directa o inversa, atendiendo a su constante. Enseguida te planteamos una situación en la que se mostraran distintas estrategias de solución.
Isaac se transporta en motocicleta y ha realizado un registro de las distancias que recorre con cierta cantidad de litros de gasolina.
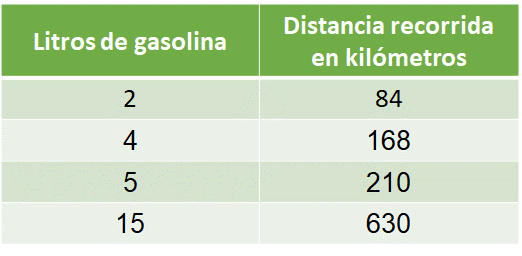
En la tabla se registró que, con 2 litros de gasolina recorrió 84 kilómetros; con 4 litros recorrió 168 kilómetros; con 5 litros, 210 kilómetros, y con 15 litros, 630 kilómetros.
A partir de estos datos, contesta.
- ¿Qué tipo de relación se observa entre sus magnitudes?
- ¿Cuántos kilómetros esperaría recorrer con 3, 7 y 10 litros de gasolina?
En la tabla puedes observar que con el doble de la cantidad de gasolina se recorrió el doble de la distancia, es decir, 4 litros es el doble de 2 litros, y 168 kilómetros es el doble de 84 kilómetros. Asimismo 15 litros es el triple de 5 litros y 630 kilómetros es el triple de 210 kilómetros.
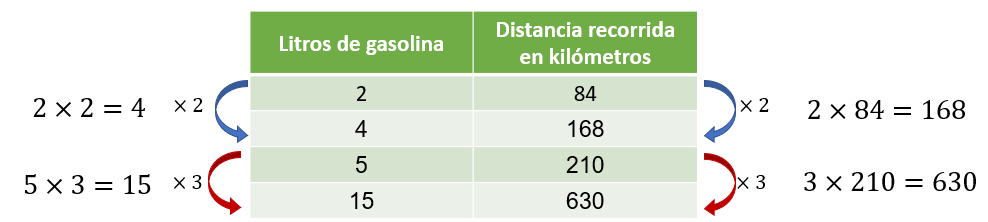
Como las magnitudes aumentan en la misma proporción, entonces, se trata de una situación de proporcionalidad directa.
Otra forma de saber qué tipo de relación existe entre las magnitudes es calculando la constante de proporcionalidad. Para ello, se divide el valor de la segunda magnitud, en este caso la cantidad de kilómetros recorridos, entre el valor correspondiente de la primera magnitud, que aquí son los litros de gasolina.
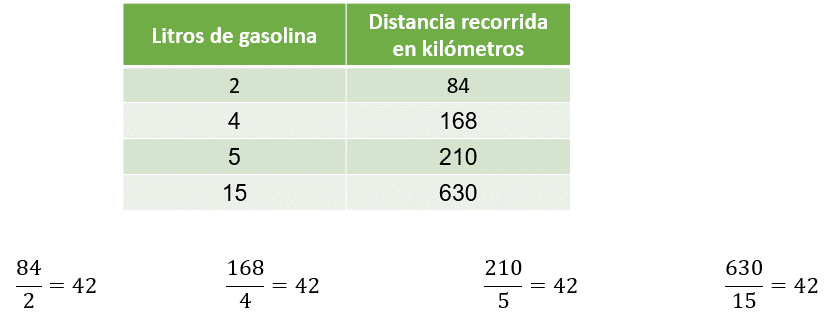
De esta manera, observamos que el cociente es 42, es decir, es un valor constante, entonces, con esto se verifica nuevamente que se trata de una situación de proporcionalidad directa.
Ahora, ayuda a Isaac a determinar cuántos kilómetros esperaría recorrer con 3, 7 y 10 litros de gasolina. Para esto, organiza los datos en una tabla, ¿qué procedimiento seguirías para completar las distancias faltantes?
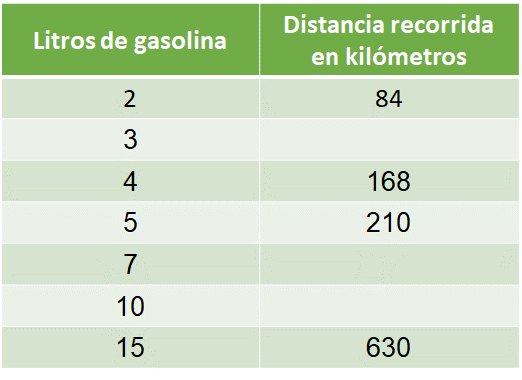
Una manera es emplear un método aditivo o sustractivo. En él se suman o restan dos magnitudes conocidas que den como resultado el valor del dato desconocido.
De esta manera, para determinar la distancia que se recorre con 3 litros, se combinan dos valores de la primera magnitud por medio de la adición o sustracción que dé como resultado 3, y se hace la misma combinación con la segunda magnitud para calcular el valor faltante.
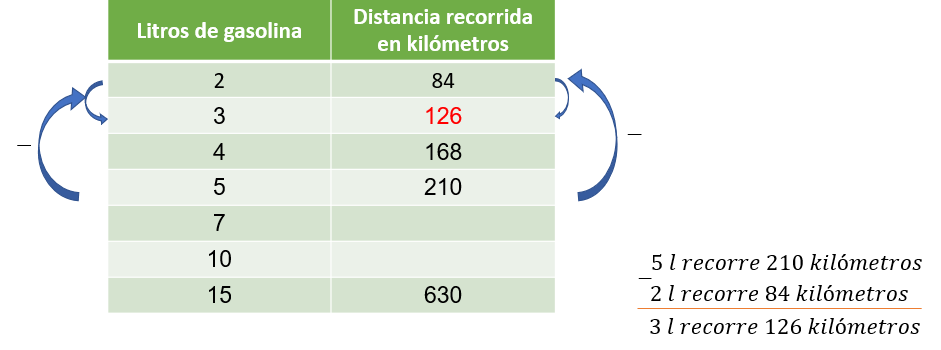
Por tanto, a 5 se restan 2 para obtener 3, y a 210 se resta 84, lo que resulta 126. Esto quiere decir que, con 3 litros de gasolina se recorrerán 126 kilómetros.
Ahora, para obtener la distancia correspondiente a 7 kilómetros, se puede sumar 2 más 5, y sus cantidades correspondientes, 84 más 210. La suma de 84 con 210 resulta 294.
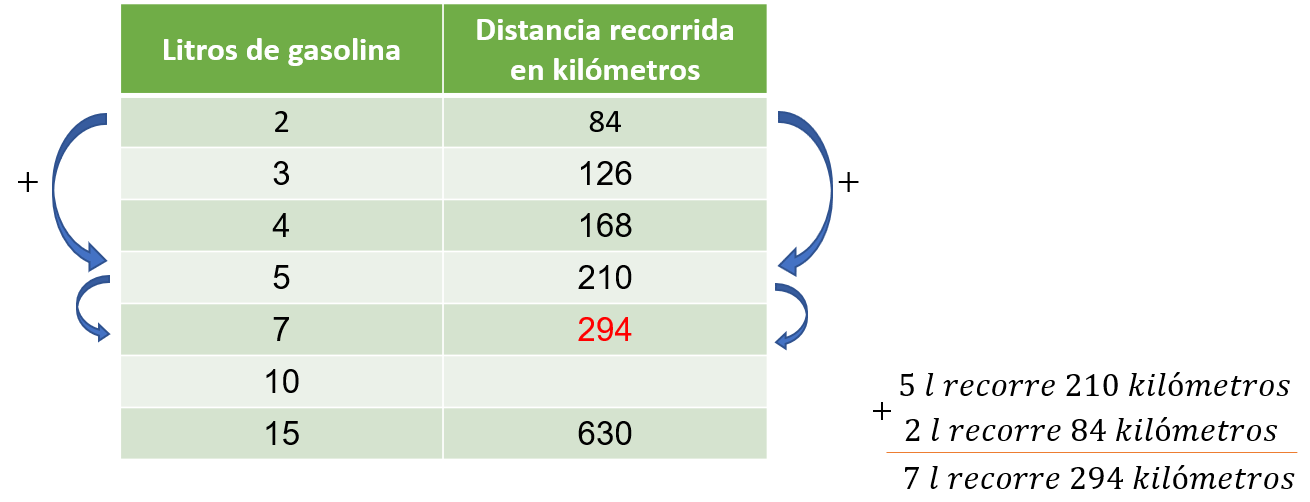
Esto quiere decir que, con 7 litros de gasolina, se esperaría recorrer 294 kilómetros.
Finalmente, para obtener la distancia recorrida que corresponde a 10 litros de gasolina, se pueden sumar 3 con 7 y de la segunda magnitud, se suman 126 con 294.
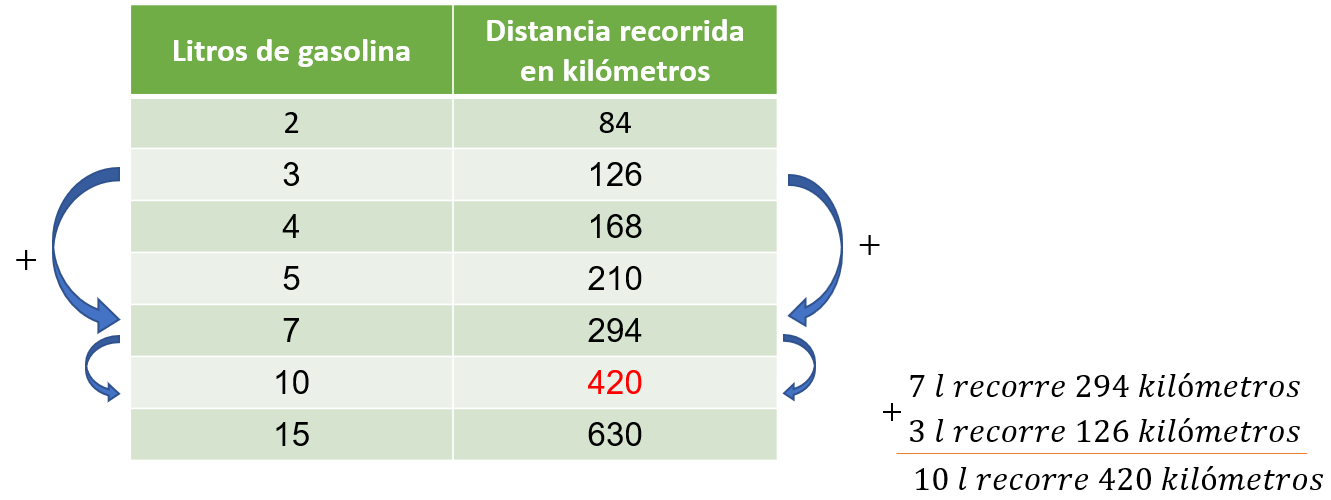
Esta segunda suma resulta 420. Lo que indica que, con 10 litros de gasolina se espera recorrer 420 kilómetros.
Ésta no es una combinación única, también se pudo haber restado 15 menos 5, o sumado 2 más 3, más 5, para generar 10, y con la segunda magnitud se realizan las mismas operaciones con los valores correspondientes.
Revisa otro procedimiento que se puede usar para calcular las distancias recorridas. Este consiste en hacer uso del valor unitario.
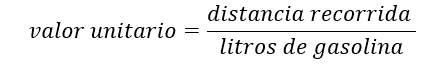
Lo primero que se hace es calcular la distancia recorrida con un litro de gasolina, entonces dividimos los kilómetros recorridos entre los correspondientes litros de gasolina.
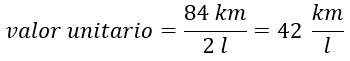
Lo que significa que por cada litro de gasolina se pueden recorrer, bajo las mismas condiciones, 42 kilómetros.
Después, este valor unitario, que es la constante de proporcionalidad, se debe multiplicar por la cantidad de litros de gasolina que corresponda a los valores faltantes.
Por lo tanto, para 3 litros de gasolina, multiplicamos 3 litros por 42 kilómetros por litro que resulta 126 kilómetros, después de simplificar la unidad “litros” que aparece en el numerador y denominador.
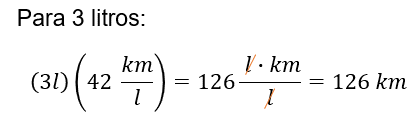
Ahora, para 7 litros de gasolina, se multiplica, 7 litros por 42 kilómetros por litro, que es igual a 294 kilómetros.
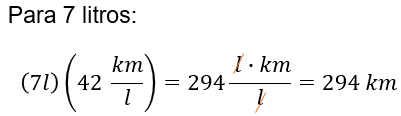
Lo mismo se hace para 10 litros de gasolina.
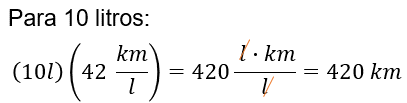
Con ambos procedimientos se obtuvieron los mismos resultados.
A continuación, revisa un tercer procedimiento para hallar valores faltantes en una proporcionalidad directa.
Este procedimiento es la regla de tres, el cual consiste en establecer una proporción, en la que hace falta un dato.
Para 3 litros establecemos una proporción en que hay un valor faltante. Por ejemplo, 2 litros es a 84 kilómetros como 3 litros es a “x”, que representa la distancia buscada.

De ahí se puede establecer la igualdad 21 entre 84 kilómetros es igual a 31 entre “x” y se tiene que “x” es igual a 84 kilómetros por 3 litros, entre 2 litros, que es igual a 252 kilómetros por litro, entre 2 litros, de donde se obtiene que “x” es igual a 126 kilómetros.
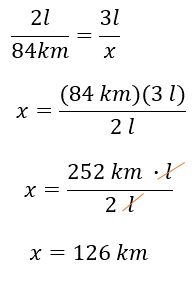
Para 7 litros, se puede establecer la siguiente regla de tres, 5 litros es a 210 kilómetros como 7 litros es a “x”.
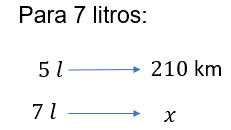
Al resolver la regla de tres, tenemos que “x” es igual a 210 kilómetros por 7 litros, entre 5 litros. De ahí se tiene que “x” es igual a 1 470 kilómetros por litro entre 5 litros.
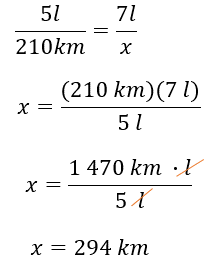
De donde se obtiene que “x” es igual a 294 kilómetros, es decir, que con 7 litros de gasolina se esperaría recorrer 294 kilómetros.
Ahora, para obtener la distancia recorrida con 10 litros de gasolina, se puede establecer la siguiente regla de tres.
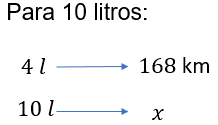
Por lo tanto, “x” es igual al cociente del producto de 168 kilómetros por 10 litros, entre 4 litros, que es igual a 1 680 kilómetros por litro entre 4 litros. Después de simplificar la unidad “litros” y calcular el cociente, tenemos que “x” es igual a 420 km.
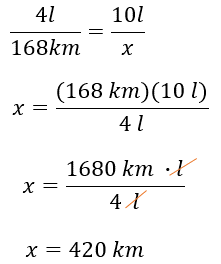
Nuevamente se obtienen los mismos resultados para las distancias desconocidas.
Por tal razón, para resolver situaciones en las que interviene la proporcionalidad directa, no existe un único procedimiento.
Ahora resuelve la siguiente situación.
Zoé vende alimento para perro. Esta semana compró dos bultos de 25 kilogramos cada uno. Si hace paquetes con 5 kilogramos, ¿cuántos puede obtener de los dos bultos? ¿Y si fueran de 2 kilogramos, de 1 kilogramo, de 1/2 kilogramo o de 1/4 de kilogramo?
¿Qué tipo de relación existe entre las magnitudes?
Para contestar la última pregunta y decidir lo que debes hacer para resolver este problema, piensa si aumenta la cantidad de alimento en los paquetes, ¿el número de paquetes aumenta o disminuye?
Si aumenta la cantidad de alimento en los paquetes, el número de paquetes disminuye.
Si aumenta la cantidad de alimento en los paquetes al doble o al triple, ¿el número de paquetes disminuye a la mitad o a la tercera parte?
Si aumenta la cantidad de alimento en los paquetes al doble o al triple, el número de paquetes disminuye a la mitad o a la tercera parte.
Dado que se cumplen las dos condiciones anteriores, podemos afirmar que esta situación corresponde a una proporcionalidad inversa.
Para determinar el número de paquetes, te auxiliarás de una tabla registrando en la primera columna los kilogramos por paquete y, en la segunda columna, el número de paquetes que se pueden obtener de los dos bultos de alimento.
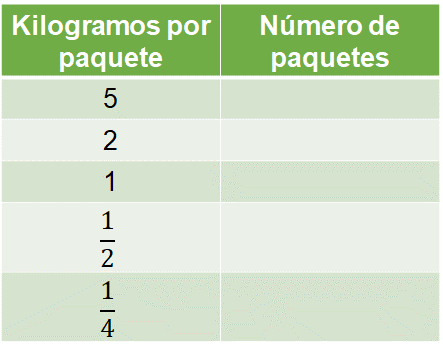
Una manera de iniciar la resolución del problema es considerar que se tienen 2 bultos de alimento, cada uno con 25 kilogramos de alimento. Entonces, en total se tienen 50 kilogramos de alimento con el que se desean hacer paquetes con diferente contenido.
Con esta información se puede afirmar que, si se hacen paquetes de 1 kilogramo cada uno, se podrán obtener 50 paquetes.
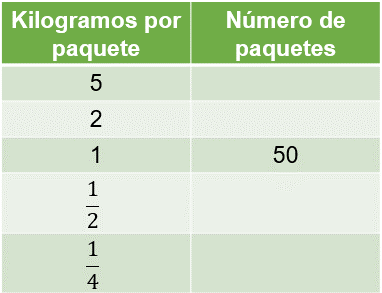
Para calcular el número de paquetes que se pueden obtener de 2 kilogramos de alimento, se multiplica 1 de la primera columna por 2 para obtener 2 y se divide entre 2 el valor correspondiente a 1 kilogramo por paquete.
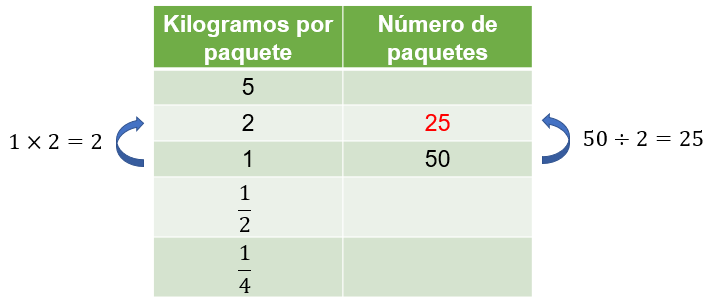
De esta manera se puede afirmar que tendremos 25 paquetes de 2 kilogramos cada uno.
Para determinar el número de paquetes con 5 kilogramos de alimento cada uno, se multiplica 1 kilogramo por 5 para obtener 5 kilogramos, y lo correspondiente a 1 kilogramo de la segunda columna se divide entre 5 obteniendo 10 paquetes.
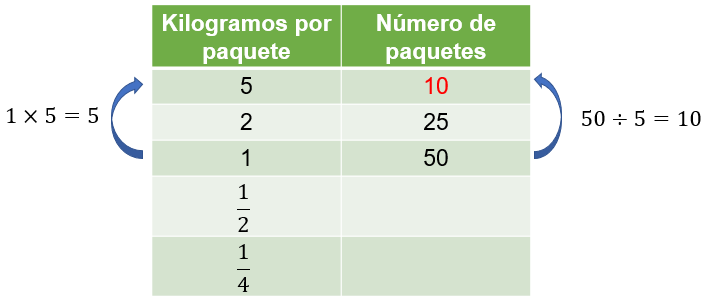
Para calcular el número de paquetes con medio kilogramo de alimento cada uno, se divide 1 kilogramo entre 2 para obtener medio kilogramo, y lo correspondiente a 1 kilogramo de la segunda columna se multiplica por 2, obteniendo 100 paquetes.
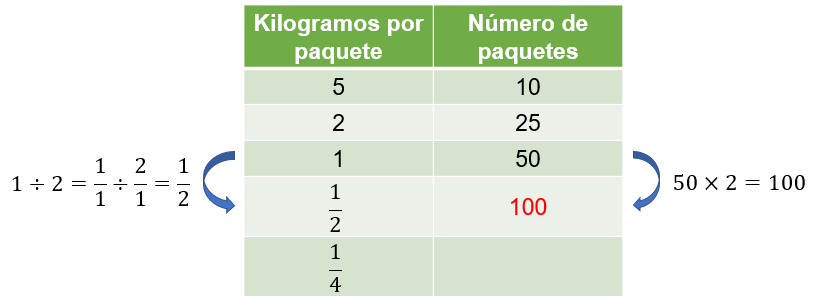
Finalmente, para determinar el número de paquetes con un cuarto de kilogramo de alimento cada uno, se divide 1 kilogramo entre 4 para obtener un cuarto de kilogramo, y lo correspondiente a 1 kilogramo de la segunda columna, se multiplica por 4 obteniendo 200 paquetes.
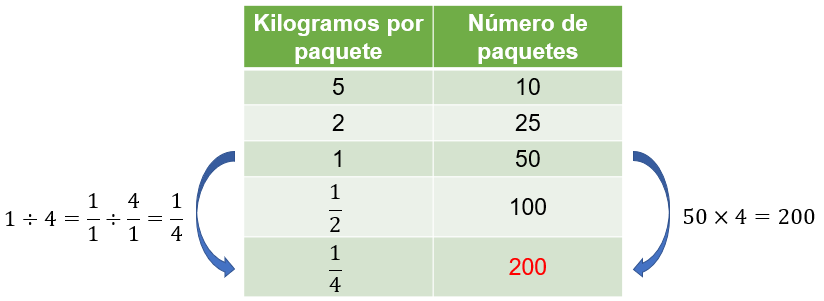
Así, hemos calculado el número de paquetes que se pueden obtener si se coloca determinada cantidad de alimento en cada uno.
Analiza otro método para determinar estos mismos valores. Usarás la regla de tres a la inversa, para encontrar nuevamente los valores faltantes.
Dado que se trata de una situación de proporcionalidad inversa, puedes establecer una regla de tres. De manera que, una de ellas es, paquetes de 2 kilogramos es a “x” número de paquetes, como paquetes de 1 kilogramo es a 50 paquetes.
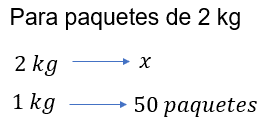
De donde “x” es igual al producto de 1 kilogramo por 50 paquetes, entre 2 kilogramos. De aquí, “x” es igual a 50 kilogramos por paquetes entre 2 kilogramos. Simplificando la unidad “kilogramos” del numerador y denominador obtenemos “x” igual a 25 paquetes.
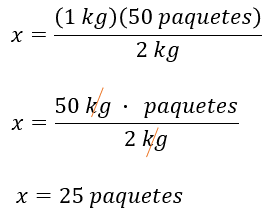
Para paquetes con 5 kilogramos tenemos la regla 5 kilogramos es a “x” número de paquetes como paquetes de 2 kilogramos es a 25 paquetes.
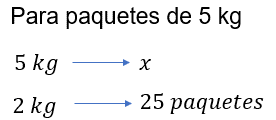
De donde se tiene que “x” es igual 2 kilogramos por 25 paquetes, entre 5 kilogramos. De aquí, “x” es igual a 50 kilogramos por paquetes, entre 5 kilogramos. Al resolver la división y simplificar unidades comunes del numerador y denominador tenemos por resultado “x” igual a 10 paquetes.
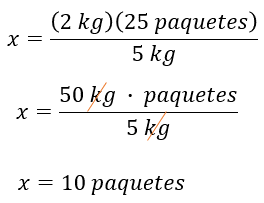
Para determinar el número de paquetes con medio kilogramo, establecemos la regla 5 kilogramos es a 10 paquetes como medio kilogramo es a “x” número de paquetes.
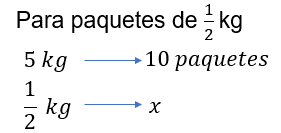
De lo anterior, se tiene que “x” es igual 5 kilogramos por 10 paquetes, entre medio kilogramo, obteniendo “x” igual a 50 kilogramos por paquetes, entre medio kilogramo. Luego simplificamos las unidades comunes en el numerador y el denominador y resolvemos la división, de donde se obtiene que “x” es igual a 100 paquetes.
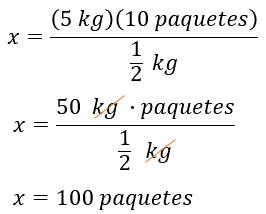
Finalmente, para determinar el número de paquetes de un cuarto de kilogramo, se forma la siguiente regla de tres, 2 kilogramos es a 25 paquetes como un cuarto de kilogramo es a “x” números de paquetes.
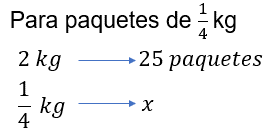
De lo anterior se tiene que “x” es igual 2 kilogramos por 25 paquetes, entre un cuarto de kilogramo, obteniendo “x” igual a 50 kilogramos por paquetes, entre un cuarto de kilogramo. Luego simplificamos las unidades comunes en el numerador y el denominador y resolvemos la división, de donde se obtiene que “x” es igual a 200 paquetes.
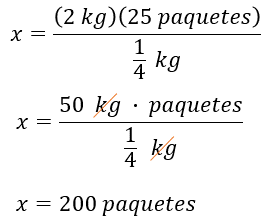
Nuevamente, los valores que se obtuvieron con ambos procedimientos son iguales.
Se pueden verificar los valores obtenidos aplicando el criterio de la constante de proporcionalidad, en la que los productos entre los valores de las magnitudes correspondientes deben ser iguales.
Se multiplican los valores de la primera columna con su correspondiente valor de la segunda columna.

En todos los casos, el producto es 50, por tal razón decimos que los valores son correctos al tratarse de una relación de proporcionalidad inversa.
La proporcionalidad es uno de los contenidos matemáticos que está presente en casi todos los niveles escolares, ya que es de uso cotidiano, además de ser un elemento importante en el estudio de los fenómenos de la naturaleza o de las sociedades.
El razonamiento proporcional no se limita sólo al uso de la regla de tres como método de resolución, sino que hay varios métodos que cumplen con este fin.
Por tal motivo, en esta sesión se hizo uso de otros procedimientos, pero, sobre todo, debes rescatar las estrategias personales que es conveniente formalizar a través del estudio de las matemáticas.
Este es un material de apoyo y, para seguir aprendiendo más sobre este contenido, puedes consultar otras fuentes bibliográficas, además de tu libro de texto para la asignatura de Matemáticas, segundo grado.
El reto de hoy:
Reflexiona sobre el uso del razonamiento proporcional, busca situaciones que te permitan la implementación de este recurso.
Comparte tus reflexiones y dudas con tu profesora o profesor en el trabajo que realizas a distancia.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas