La probabilidad teórica y la probabilidad frecuencial
La probabilidad teórica y la probabilidad frecuencial
Aprendizaje esperado: determina la probabilidad teórica de un evento en un experimento aleatorio.
Énfasis: identificar las diferencias entre la probabilidad teórica y la probabilidad frecuencial.
¿Qué vamos a aprender?
Continuarás con el estudio de la probabilidad. En esta sesión, identificarás las diferencias entre la probabilidad teórica y la probabilidad frecuencial. Asimismo, conocerás cómo se aplica y las características de cada una.
¿Qué hacemos?
Para iniciar, analiza una situación en la que puedas comparar a la probabilidad teórica o clásica, con la probabilidad frecuencial o experimental.
Situación, moneda al aire
Cecilia y Santiago quieren predecir cuál de las caras obtendrán al lanzar una moneda al aire.
¿Cómo puedes realizar esta predicción?
Para realizar esta predicción sin realizar ningún lanzamiento es necesario determinar la probabilidad teórica. Pero ¿cómo puedes determinarla?
La probabilidad teórica “P” de que ocurra un evento “e” es igual al número de eventos favorables, dividido entre el número total de eventos asociados a un experimento aleatorio.
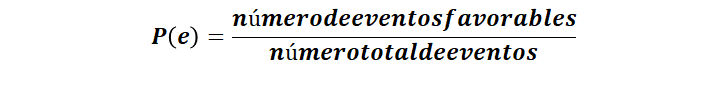
Y para determinar el número total de eventos, es necesario identificar al espacio muestral “omega”, ya que con él puedes identificar cuántos y cuáles son los eventos totales.
Para el lanzamiento de una moneda, el espacio muestral “omega” está conformado por dos eventos: águila y sol.
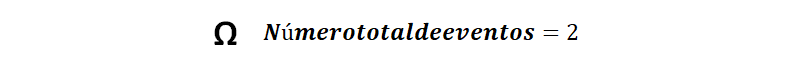
Con esta información, Cecilia y Santiago pueden determinar:
Primero, cuál es la probabilidad teórica de obtener águila al lanzar una moneda, y posteriormente, cuál es la probabilidad de obtener sol.
Para determinar la probabilidad de obtener águila al lanzar una moneda, analiza cuántos eventos favorables hay en el espacio muestral, en este caso sólo hay uno, que es águila. Entonces, como el número de eventos favorables es 1 y el número total de eventos es 2, la probabilidad de obtener águila es igual a 1 entre 2, o 0.5, equivalente al 50 por ciento.

Asimismo, para determinar la probabilidad de obtener sol al lanzar una moneda, hay un evento favorable que es sol en el espacio muestral. Entonces, como el número de eventos favorables es 1 de 2, la probabilidad de obtener sol también es igual a 1 entre 2, o 0.5, equivalente al 50 por ciento.

Se puede concluir que la probabilidad teórica de que caiga águila es del cincuenta por ciento, y que la probabilidad teórica de obtener un sol, al lanzar una moneda, es también del 50 por ciento.
Pero, Cecilia y Santiago quieren corroborar que, si realizan 10 lanzamientos de la moneda, obtendrán que el 50 por ciento de las veces caerá águila y el otro 50 por ciento caerá sol.
¿Qué piensas que ocurrirá?
¿Serán iguales la probabilidad teórica y la experimental?
Cecilia y Santiago, deciden lanzar en repetidas ocasiones la moneda al aire y confirmar su suposición. En los primeros diez lanzamientos, 7 veces cayó águila y 3 veces cayó sol.

¿Cuál es la probabilidad frecuencial de que al lanzar la moneda caiga águila o sol, de acuerdo con los lanzamientos que realizaron Cecilia y Santiago?
Primero recuerda que la probabilidad frecuencial “Pf” de que ocurra un evento “e” es igual al número de eventos favorables en el experimento, entre el número total de intentos.
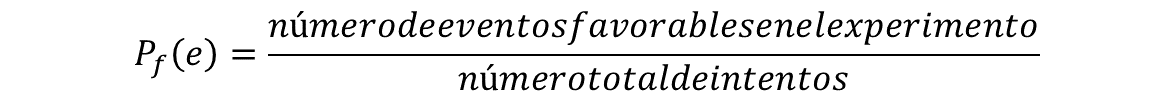
Regresando al análisis, de acuerdo con los lanzamientos que realizaron Cecilia y Santiago, la probabilidad experimental o frecuencial de que caiga águila es 7 eventos favorables, en el experimento, de un total de 10, esto es 0.7, que representa el 70 por ciento.
De la misma forma, la probabilidad frecuencial de que caiga sol es: 3 casos favorables en el experimento, entre el número total de intentos que son 10, esto es 3 entre 10 o 0.3, correspondiente al 30 por ciento.
Para comparar los resultados de la probabilidad teórica con los de la probabilidad frecuencial, anótalos en dos tablas. En una incluye los resultados de la probabilidad teórica y en la otra, los de la probabilidad frecuencial.
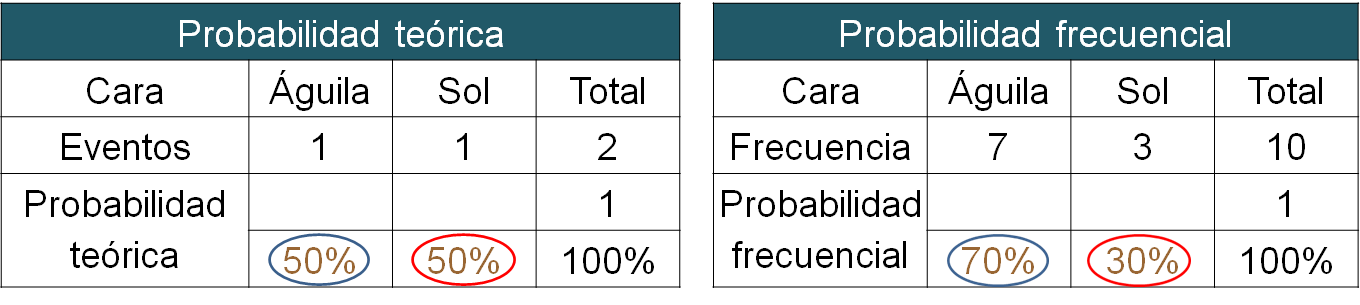
¿Cómo son la probabilidad teórica y la probabilidad frecuencial para el lanzamiento de una moneda de acuerdo con los resultados obtenidos por Cecilia y Santiago?
Se identifica que son diferentes, porque la probabilidad teórica se basa en una situación teórica, mientras que la frecuencial, es el resultado de la práctica.
Analiza los resultados adquiridos:
La probabilidad teórica de obtener un águila es del 50 por ciento, mientras que la probabilidad frecuencial, para los 10 lanzamientos que realizaron Cecilia y Santiago, fue del 70 por ciento. De la misma forma, la probabilidad teórica de obtener un sol es del 50 por ciento, mientras que la probabilidad frecuencial obtenida por Cecilia y Santiago fue del 30 por ciento.
Reflexiona:
¿Qué fue lo que hicieron Cecilia y Santiago para obtener ambas probabilidades?
Para responder, te puedes guiar de los siguientes cuestionamientos:
¿Qué consideraron Cecilia y Santiago para determinar la probabilidad teórica?
Y, ¿qué consideraron para determinar la probabilidad frecuencial?
Para obtener la probabilidad teórica, consideraron únicamente, las características de la moneda. Y para obtener la probabilidad frecuencial, lanzaron la moneda 10 veces y anotaron la frecuencia con la que se obtuvo águila o sol, esto quiere decir que tuvieron que experimentar para poder obtenerla.
Entonces, Cecilia y Santiago, al darse cuenta de que las probabilidades teórica y frecuencial no fueron iguales, deciden lanzar la moneda 10 veces más y sumar los resultados a los 10 lanzamientos anteriores.
Con estos nuevos lanzamientos, ¿lograrán igualar la probabilidad teórica de obtener un águila o un sol, con su correspondiente probabilidad frecuencial?
Revisa lo que sucede. En los siguientes 10 lanzamientos de Cecilia y Santiago, se obtuvieron 6 veces águila y 4 veces sol. Al incluirlos con los primeros diez lanzamientos, se tiene que el número total de veces que cayó águila es de 13. Asimismo, el número total de veces que cayó sol es de 7.
Entonces, la probabilidad frecuencial de obtener águila, de acuerdo con los resultados de Cecilia y Santiago, es el número de eventos favorables: 13, entre el número de eventos totales: 20; que es equivalente a 0.65 o al 65 por ciento. Y la probabilidad de obtener un sol, es de 7 entre 20, es decir, 0.35 o su equivalente del 35 por ciento.
¿Cambió la probabilidad frecuencial o permaneció constante?
Compara con la siguiente tabla dichas probabilidades frecuenciales, y determínala.
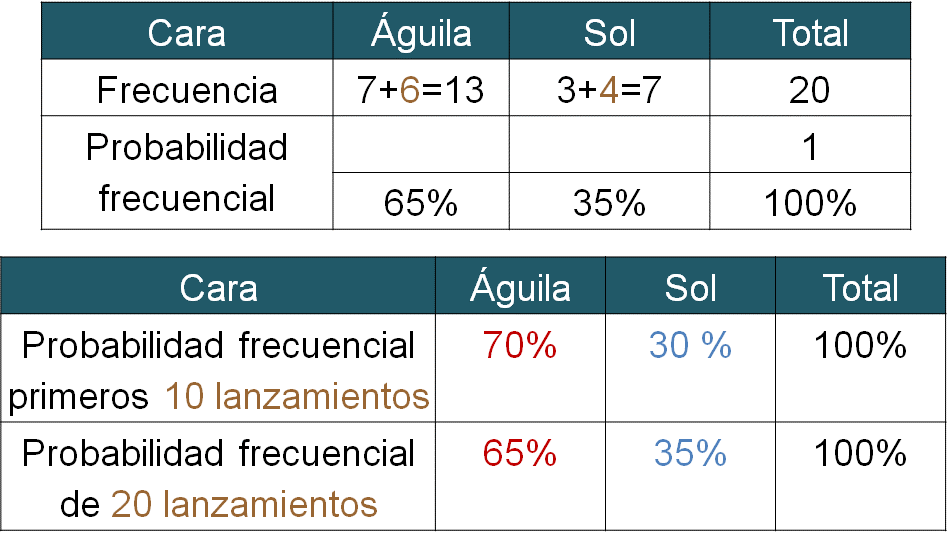
En los primeros 10 lanzamientos, la probabilidad frecuencial de que caiga águila es del 70 por ciento; pero, si se consideran los otros 10 lanzamientos, la probabilidad frecuencial de que caiga águila disminuyó al 65 por ciento.
Y, ¿qué sucedió con la probabilidad frecuencial de que caiga sol?
En los primeros 10 lanzamientos, la probabilidad frecuencial de que caiga sol es del 30 por ciento, y al considerar los otros 10 lanzamientos, ésta aumentó al 35 por ciento.
¿Qué fue lo que sucedió?
La probabilidad frecuencial para obtener un águila disminuyó y para obtener un sol aumentó.
Ahora analiza, ¿qué va a suceder si el número de lanzamientos aumenta?, ¿cómo variará la probabilidad frecuencial de que caiga águila o sol?
Cecilia y Santiago se hicieron estas preguntas y decidieron aumentar el número de lanzamientos.
Cecilia y Santiago, deciden realizar un total de 100 lanzamientos de los cuales, 47 cayeron águila y 53 cayeron sol.
¿Cuál es la probabilidad frecuencial de que caiga águila de acuerdo con los 100 lanzamientos?
Es 47 entre 100, 0.47 o 47 por ciento.
Y, ¿cuál es la probabilidad frecuencial de que caiga sol, de acuerdo con los 100 lanzamientos?
Es 53 entre 100, 0.53 o 53 por ciento.
Ahora, compara lo que ha pasado con la probabilidad frecuencial cuando el número de lanzamientos aumenta.
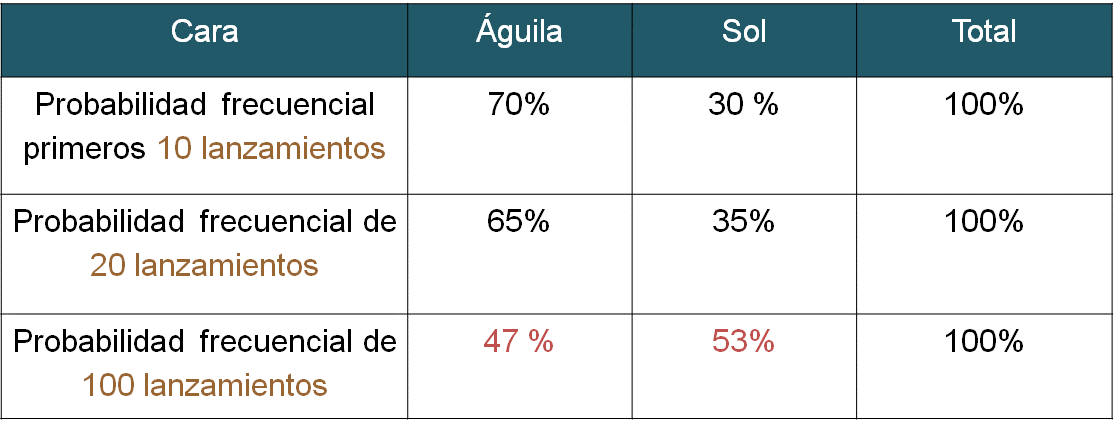
Se observa que la probabilidad frecuencial de obtener águila se va acercando a la probabilidad frecuencial de obtener un sol.
Entonces, si Cecilia y Santiago continúan realizando muchos más lanzamientos, ¿qué es lo que se puede esperar?
Por un lado, se observa que cuando el número de lanzamientos va aumentando, la probabilidad frecuencial de caer águila se acerca cada vez más a la probabilidad frecuencial de obtener un sol y, como consecuencia de ello, cuando el número de lanzamientos es cada vez mayor, la probabilidad frecuencial se acerca cada vez más a su probabilidad teórica. Por ello, se puede inferir que, si se aumenta el número de lanzamientos, la probabilidad frecuencial de obtener águila estará cada vez más cercana al 50 por ciento. Y lo mismo ocurrirá con la probabilidad de obtener sol.
Has analizado una situación en la que comparaste a la probabilidad teórica con la frecuencial. Identificaste que cuando un mismo experimento se repite en varias ocasiones, la probabilidad frecuencial se aproxima a la probabilidad teórica en los resultados.
Además del lanzamiento de una moneda, ¿en qué otras situaciones se pueden comparar a la probabilidad teórica con la experimental?
Para contestar a esta pregunta, analiza la siguiente situación.
Situación, cartas
Eugenia y Felipe tienen cuatro cartas, cada una de ellas tiene un color diferente. Los colores de sus cartas son: azul, amarillo, verde y rojo.
Sustraen una de las cartas, registran su resultado, regresan la carta, y las revuelven para repetir la sustracción. Los resultados de su experimento se muestran en la siguiente tabla de frecuencias:

De acuerdo con los resultados de Eugenia y Felipe, ¿cuál es la probabilidad de que, al sustraer una carta, ésta sea de color verde?
Para determinarlo, debes saber cuál fue el total de sustracciones que ellos realizaron.
Observa la tabla y determínalo. El total de sustracciones que se realizaron es: 18 más 22 más 17 más 23 igual a 80.

Entonces la probabilidad frecuencial de que, al sustraer una carta, ésta sea de color verde es: su frecuencia 17, entre el total 80, que es igual a dos mil ciento veinticinco diez milésimos, que representa el 21.25 por ciento del total de las sustracciones. Sin embargo, no era lo que Eugenia y Felipe pensaban que iba a salir.
Como hay cuatro cartas, esperaban que la probabilidad fuera del 25 por ciento porque cada carta de un color representa la cuarta parte de ellas.
Entonces, Eugenia y Felipe deciden realizar 200 sustracciones y averiguar lo que sucederá.
En la siguiente tabla se muestran los resultados de las 200 sustracciones.

Entonces, la probabilidad frecuencial de que al sustraer una carta ésta sea de color verde es: su frecuencia 55, entre el total 200, que es igual a doscientos setenta y cinco milésimos, que representa el 27.5 por ciento del total de las sustracciones.
Al comparar ambas probabilidades frecuenciales para diferente número de sustracciones, se observa que la diferencia entre estas probabilidades, aún no se acercan mucho a la probabilidad teórica, que es del 25 por ciento.

Por ello, Eugenia y Felipe deciden realizar 500 sustracciones y averiguar si con ese número de sustracciones la probabilidad frecuencial se acerca a la probabilidad teórica o no. Sus resultados se muestran en la siguiente tabla.

Nuevamente, la probabilidad frecuencial de que, al sustraer una carta, ésta sea de color verde es: su frecuencia 126, entre el total 500, que es igual a doscientos cincuenta y dos milésimos, que representa el 25.2 % del total de las sustracciones.
Al comparar a la probabilidad frecuencial de sustraer una carta de color verde con diferente número de sustracciones, se observa que cuando es mayor el número de sustracciones, para estos datos primero aumentó y posteriormente disminuyó, pero tiende al 25 por ciento.

Cuando se compara esta probabilidad frecuencial con 500 extracciones del 25.2 por ciento, con la probabilidad teórica de sustraer la carta de color verde, del 25 por ciento, Eugenia y Felipe deciden no realizar más sustracciones y se dan cuenta que, para que se acerquen los valores numéricos de estas probabilidades, se deben realizar un número considerable de veces dichas sustracciones. Es entonces cuando la probabilidad frecuencial tiende a la probabilidad teórica.
A continuación, examina otra situación.
Situación, moneda y dado
Cuando se lanza una moneda y un dado al aire, a la par, ¿cuál es la probabilidad teórica de obtener un águila y un número par al mismo tiempo?
Como ya lo habías revisado, primero necesitas identificar cuáles son todos los resultados posibles, es decir, cuál es el espacio muestral. En este caso, el espacio muestral “omega” es igual a:
Águila-1, águila-2, águila-3, águila-4, águila-5, águila-6, sol-1, sol-2, sol-3, sol-4, sol-5 y sol-6.
Con el espacio muestral, te puedes dar cuenta que hay seis eventos en los que puede caer águila con alguno de los números del dado y otros seis eventos en los que puede caer sol, también con alguno de los números del dado. En total hay 12 diferentes resultados posibles.
Ahora, del espacio muestral, selecciona aquellos eventos en los que se cumpla que caiga águila y también un número par. Al analizar el espacio muestral se encuentra que puede caer:
Águila-2, águila-4 y águila-6.
Por lo tanto, se tienen 3 eventos favorables de un total de 12.
Entonces, la probabilidad teórica de obtener un águila y un número par es de 3 entre 12, o su equivalente de un cuarto o de 0.25, que representa el 25% del total de eventos.
Hay que tener presente que, no se ha realizado ningún lanzamiento; sin embargo, por la característica que tiene la moneda de tener dos caras y el dado seis, se sabe que hay un total de doce resultados posibles y que tres de ellos son eventos favorables para la especificación, que la cara de la moneda sea águila y el número del dado sea par, por ello, se dice que lo que se está determinando es la probabilidad teórica, porque se puede determinar sin necesidad de realizar algún experimento.
Esto significa que, para obtener la probabilidad frecuencial de cualquier evento, es necesario que se realicen los lanzamientos y que se registren los resultados. Debes recordar que, a la probabilidad frecuencial, también se le llama experimental, porque se requiere de la realización del experimento.
Al realizar el experimento y lanzar 1 000 veces una moneda y un dado se obtiene:
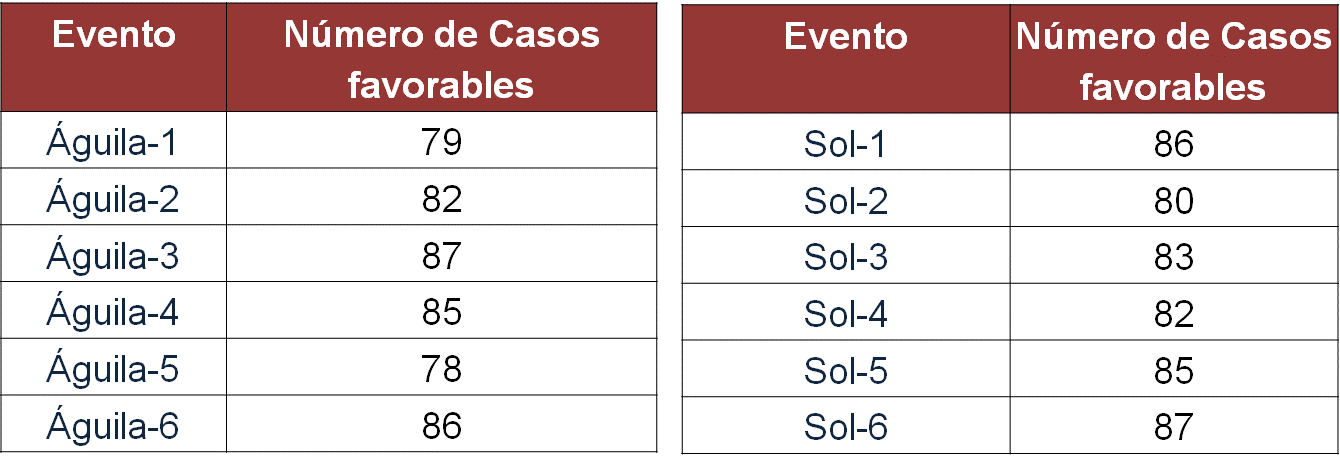
Entonces, la probabilidad frecuencial de que caiga águila y par es: la frecuencia con la que ocurrió águila-2 que fue de 82 más, la frecuencia con la que cayó águila-4 que fue de 85 más, la frecuencia con la que ocurrió águila-6 que fue de 86, dividido entre 1000. Esto es 253 casos favorables entre 1000, que representa un 25.3 por ciento del total de los casos.

Recuerda que la probabilidad teórica para este evento fue del 25%, mientras que la experimental para 1000 lanzamientos es del 25.3%. Puedes observar que ambas probabilidades son muy parecidas.
Ahora, examina dentro de este experimento otro caso:
¿Cuál es la probabilidad teórica y frecuencial de que, al lanzar una moneda y un dado, caiga sol y seis?
Esto, de acuerdo con el número de lanzamientos que se presentaron en las tablas de frecuencia.
Para obtener la probabilidad teórica, se identifica que en el espacio muestral sólo aparece un evento favorable para sol y 6. Por lo tanto, la probabilidad teórica es 1 evento favorable entre 12 eventos totales, que aproximadamente representa el 8.33 por ciento del total de los eventos.
Y para la probabilidad frecuencial, se divide la frecuencia de su ocurrencia en el experimento que fue de 87 entre el número total de lanzamientos que son 1000, obteniendo una probabilidad frecuencial de 87 entre 1000 que es igual a 87 milésimos, que representan el 8.7% del total de los lanzamientos.
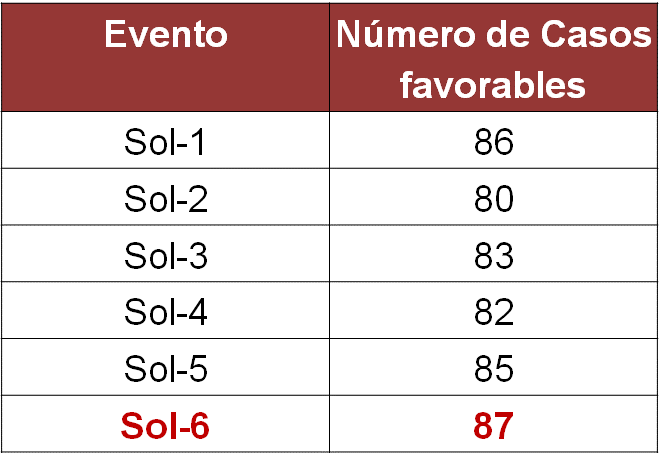
Al comparar estas dos probabilidades para el mismo evento, se observa que son muy parecidas cuando el número total de eventos es considerable.
Esto quiere decir que cuando se determina la probabilidad frecuencial de que ocurra un evento, ésta tenderá al mismo valor que el de la probabilidad teórica, siempre que el número total de eventos vaya aumentando. Y mientras mayor sea el número total de eventos, la probabilidad frecuencial tenderá más a la probabilidad teórica.
Reflexiona acerca de lo desarrollado hasta este momento.
¿Qué sucede si una persona calcula la probabilidad teórica de obtener un águila y un número par, al lanzar una moneda y un dado al mismo tiempo?
¿Qué sucede si una persona realiza 1000 veces los lanzamientos?
¿Obtendrá la misma probabilidad teórica y la misma probabilidad frecuencial que la que se acaba de desarrollar?
Para responder estos cuestionamientos, es necesario analizar de qué dependen la probabilidad teórica y la probabilidad frecuencial.
La probabilidad teórica, depende de las características de los objetos que se pretende manipular; en este caso, la moneda siempre va a tener dos caras y el dado seis caras; de forma que el número total de eventos siempre va a ser doce. Y cada uno de los 12 eventos presentes en el espacio muestral siempre va a tener la misma probabilidad de caer, de un doceavo, sin importar quien realice el cálculo.
Pero esto no ocurre con la probabilidad frecuencial, porque ésta depende de la realización del experimento, del número de eventos favorables obtenidos en el experimento y del número total de lanzamientos o sustracciones realizadas, intentos que realiza quien hace el experimento.
Y aunque los resultados de quien realiza el experimento pueden parecerse a los de otra persona, generalmente estos no son iguales.
Para concluir con la sesión, recapitula las definiciones de probabilidad teórica y de probabilidad frecuencial:
La probabilidad teórica de un evento, en un experimento aleatorio, se determina como la relación del número de eventos favorables, entre el número total de eventos.
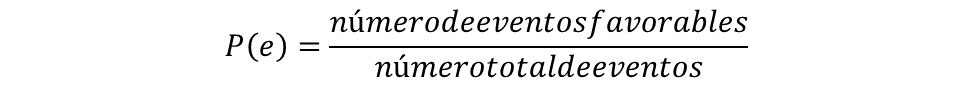
Y la probabilidad frecuencial se define como el número de eventos favorables en el experimento entre el número total de intentos.
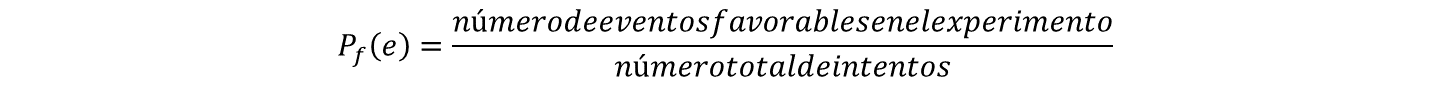
Has concluido la sesión. Recuerda consultar tu libro de texto de matemáticas de segundo grado, para profundizar en el tema.
El reto de hoy:
Corroboren que la probabilidad frecuencial tiende a la probabilidad teórica, con el siguiente experimento:
En una bolsa, que no sea transparente, mete cinco pedacitos de papel, previamente doblados, para realizar extracciones. En cada papelito anota una actividad que te guste, por ejemplo: correr, saltar, dibujar, etc.
- Determina cuál es la probabilidad teórica de que al extraer uno de los papelitos de la bolsa, se obtenga cada una de las actividades. Posteriormente, determina cuál es la probabilidad frecuencial de que al extraer uno de los papelitos, se obtengan cada una de las actividades señaladas con 10, 20 y con 30 extracciones.
- Compara tus probabilidades teóricas y experimentales, y con base en ello determina cuáles son las diferencias entre la probabilidad teórica y la experimental o frecuencial.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/