La multiplicación y la división
La multiplicación y la división
Aprendizaje esperado: consolida contenidos del eje: número, álgebra y variación.
Énfasis: integrar los contenidos del tema: multiplicación y división.
¿Qué vamos a aprender?
En esta sesión, encontrarás el significado de multiplicar y dividir números enteros, fraccionarios y decimales, comprendiendo la relación entre estas dos operaciones, así mismo utilizarás los procedimientos convencionales para resolver problemas de multiplicación y división.
¿Qué hacemos?
Para iniciar, revisarás algunos conceptos importantes de la multiplicación y división de números enteros.
Una multiplicación de dos números naturales es una suma repetida. Por ello, la multiplicación 4 por 3 se puede presentar como una suma en la que el sumando 3, se repite 4 veces o bien el sumando 4, se repite 3 veces. El resultado de ambas sumas es 12.

A partir de lo anterior, ¿qué significa 2 por 4 negativo?, ¿podemos verla como suma repetida?
La multiplicación también puede verse como una suma repetida. Ésta significa la suma de 2 veces 4 negativo y su resultado es 8 negativo.
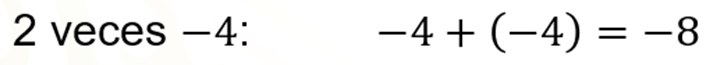
Cuando se suman números negativos, el resultado es negativo. Ahora, la multiplicación 8 negativo por 3, significa el 8 negativo sumado 3 veces, donde el resultado es 24 negativo.
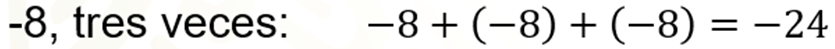
A partir de lo anterior, realiza una exploración de los signos en los productos de números enteros. Como los números naturales pueden escribirse como números enteros positivos, entonces, 4 x 3 = 12 podemos escribirlo como 4 positivo por 3 positivo igual a 12 positivo. Lo mismo se puede ver con las otras multiplicaciones que resolviste anteriormente.
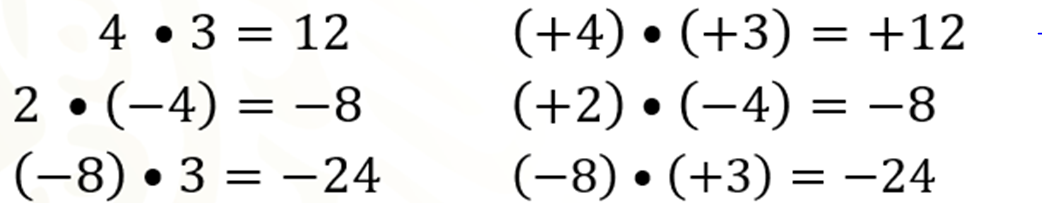
En la columna de la izquierda se ven las multiplicaciones donde al menos uno de los factores es un número natural, y en la de la derecha se ha escrito estos números como enteros positivos.
Es matemáticamente correcto escribir los números como se encuentran en la columna de la derecha, es decir, las expresiones de la izquierda son iguales a las expresiones de la derecha. Como lo escrito a la derecha ocurre con todas las multiplicaciones de números enteros, podemos decir que, cuando ambos factores son positivos, el resultado es positivo, y cuando un factor es positivo y el otro negativo, el resultado será negativo. Pero ¿qué sucede cuando los dos factores son negativos?
La multiplicación de 3 por 6 negativo resulta 18 negativo. La multiplicación de 2 por 6 negativo resulta 12 negativo. La multiplicación de 1 por 6 negativo resulta 6 negativo. La multiplicación de cero por 6 negativo resulta cero.
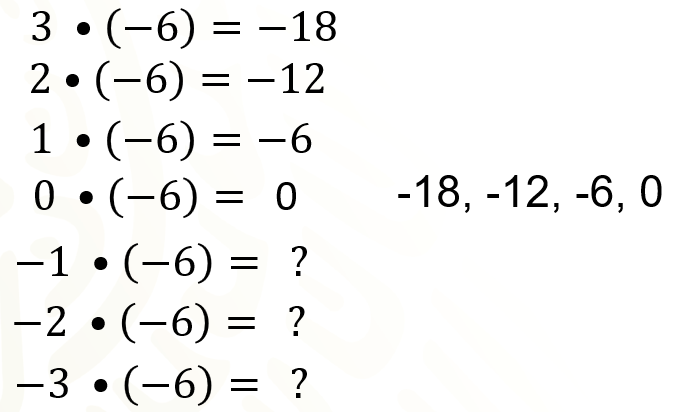
Ahora, ¿qué números deben ir en lugar de los signos de interrogación para que continué la sucesión correctamente?
En la sucesión de 18 negativo, 12 negativo, 6 negativo, cero, cada término, después del 18 negativo, se obtiene sumando 6 al anterior. Por ello podemos afirmar que los números que deben ir en el lugar de los signos de interrogación son 6, 12 y 18.
De esta manera se puede concluir que 1 negativo por 6 negativo es igual a 6 positivo, que 2 negativo por 6 negativo es igual a 12 positivo, y que 3 negativo por 6 negativo es igual a 18 positivo.
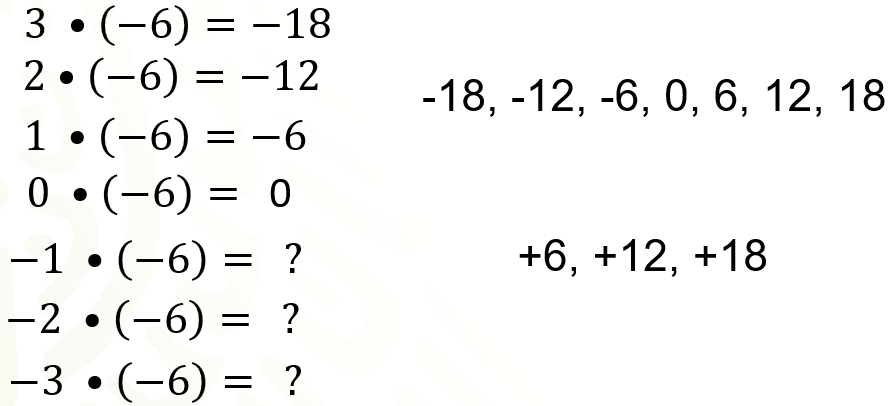
En los ejemplos, en los resultados obtenidos, se observa que, al multiplicar 2 números positivos o 2 números negativos, el resultado es positivo y al multiplicar 2 números con diferente signo, el resultado es negativo.

La tabla de la derecha se conoce como ley de los signos para la multiplicación.
Analiza ahora el caso de la división de números enteros.
La división y la multiplicación son operaciones inversas. Por eso, resolver una división corresponde a obtener el factor desconocido de una multiplicación. En las operaciones que se muestran a continuación, del lado izquierdo se han colocado multiplicaciones de enteros donde falta uno de los factores; del lado derecho, se encuentran las divisiones que cuyo cociente es igual a esos factores. Así, por ejemplo, si 2 positivo por “x” es igual a 16 negativo, entonces “x” es igual a 16 negativo entre 2 positivo, de donde se obtiene que “x” es igual a 8 negativo, porque 2 positivo por 8 negativo es igual a 16 negativo.

Sucede lo mismo con las otras multiplicaciones y divisiones, pero es necesario observar en las divisiones que, si se dividen dos números positivos o dos números negativos, el resultado es positivo, y si se dividen dos números con signos diferentes, el resultado es negativo. Es la misma ley para ambas operaciones.
Ahora revisarás conceptos importantes de la multiplicación y división, de fracciones y decimales.
Se multiplican dos fracciones. ¿Qué significa, por ejemplo, 3/4 por 2/5
El significado de esta multiplicación se comprende mejor como 3 cuartos de 2 quintos. La siguiente figura está dividida en quintos, si tomamos sólo 2 de esas partes se representa 2 quintos.
La figura está divida en cuartos, de manera horizontal, si sólo tomamos 3 de ellas, tendremos la fracción 3 cuartos. Entonces, 3 cuartos de 2 quintos está representada por la parte sombreada, dicha parte indica 6 cuadritos de los 20 que tiene toda la figura. Es decir, 3 cuartos de 2 quintos son 6 veinteavos.
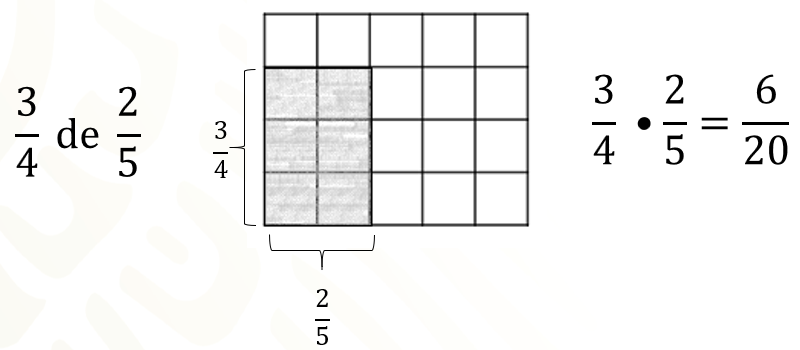
Esto quiere decir que la multiplicación de 3 cuartos por 2 quintos es igual a 6 veinteavos. Observa que, en el resultado, el numerador 6 se puede obtener de la multiplicación de los numeradores, 3 por 2 y el denominador 20 del producto, se puede obtener de multiplicar los denominadores, 4 por 5.
Analiza ahora la división de fracciones con la siguiente situación: si tenemos el cuadrado “A” que mide 12 unidades de lado, ¿cómo obtenemos el cuadrado “A” prima con lados de 9 unidades?
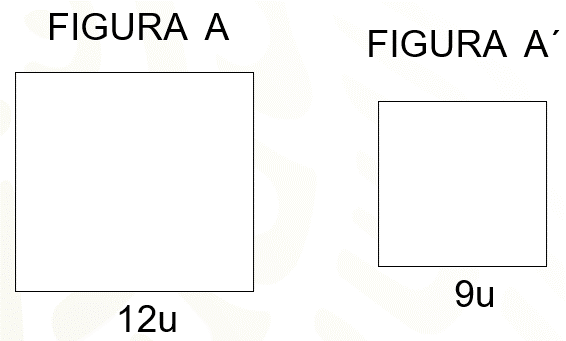
Al cuadrado “A” se ha aplicado el factor 3 cuartos, de tal manera que al multiplicar 12 por 3 cuartos se obtiene 36 cuartos, que simplificado resulta 9. Por lo tanto, 12 por 3 cuartos es igual a 9.
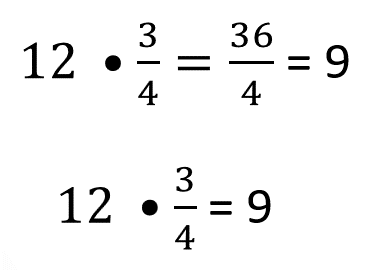
Pero ¿qué tiene que ver esto con la división de fracciones?
Para contestar esa pregunta, primero debemos preguntarnos ¿cómo recuperar la figura original?, si ahora lo que tenemos es la figura “A” prima.
Tenemos que 12 por 3 cuartos es igual a 9, que es la operación que nos llevó de la figura “A” a la figura “A” prima. Ahora bien, por otra parte, para obtener el lado de la figura original podemos aplicar operación inversa a la multiplicación que es la división, es decir, dividir 9 entre 3 cuartos y esto da por resultado 12.

Por otro lado, para revertir la trasformación de la figura “A” a la figura “A” prima, o sea, para regresar de la figura “A” prima a la figura “A” se puede aplicar el factor inverso, que es 4 tercios. El resultado de multiplicar un número y su inverso es igual a 1, por lo tanto, el inverso de 3 cuartos es 4 tercios. Así, 9 multiplicado por 4 tercios también resulta 12, como en la división.

Por una parte, 9 entre 3 cuartos es igual a 12, pero por otra, 9 por 4 tercios también es igual a 12.

Al aplicar la propiedad transitiva de la igualdad, podemos afirmar que 9 entre 3 cuartos es igual a 9 por 4 tercios. Esto quiere decir que realizar la división entre una fracción, equivale a realizar una multiplicación por el inverso de dicha fracción.
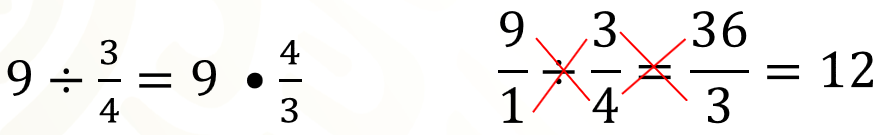
Si en lugar de convertir a la división en la multiplicación por el inverso del divisor, simplemente se multiplica de forma cruzada, como se indica con las líneas en color rojo, se obtiene el resultado correcto.
Los algoritmos usuales utilizados para resolver la multiplicación y la división se mostrarán con los siguientes ejemplos.
El producto de una multiplicación de fracciones es una fracción cuyo numerador es el producto de los numeradores de los factores y cuyo denominador es el producto de los denominadores de los factores.
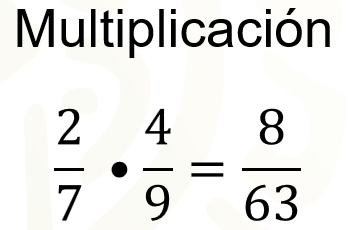
El cociente de una división de fracciones es el producto del dividendo por el inverso del divisor. En la división, también se pueden aplicar los productos cruzados.
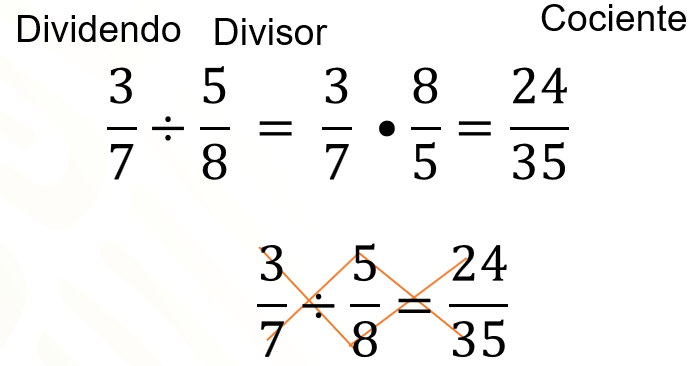
La ley de los signos para la multiplicación y para la división es válida no sólo para números enteros, sino para cualquier número real.
La primera operación es una multiplicación de una fracción por un número decimal negativo, el cual se ha convertido en la fracción negativa 6 decimos. Al multiplicar 9 por 6 resulta 54 y multiplicando 4 por 10 resulta 40, entonces 54 y 40 serán el numerador y el denominador, respectivamente, de la fracción producto, la cual es negativa, porque el producto de un número positivo por otro negativo es negativo, y convertida a número mixto es igual a un entero 7 veinteavos negativo.
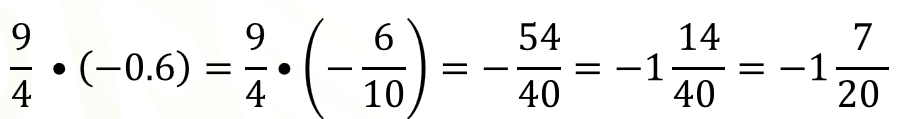
La segunda es una división de dos fracciones negativas, entonces la convertimos en una multiplicación usando el inverso del divisor, quedando 7 octavos negativos por 5 doceavos negativos, y el resultado es 35 noventaiseisavos. Como el producto de dos números negativos es positivo, la fracción resultado es positiva, aunque se puede omitir escribir el signo más.
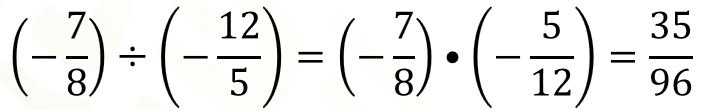
Ahora resuelve el siguiente problema.

Reflexiona. ¿Saber cuánto es 5 octavos de 2 y medio litros podrá servir para resolver el problema?, ¿qué operación utilizarías?
Esta situación se puede resolver con una multiplicación de fracciones, de hecho, la palabra “de” en este caso equivale al signo “por” de la multiplicación.
Para resolver la multiplicación antes se ha convertido 2 y medio en 5 medios. Al resolver la multiplicación se obtiene la fracción 25 dieciseisavos y ésta es igual a un entero 9 dieciseisavos.
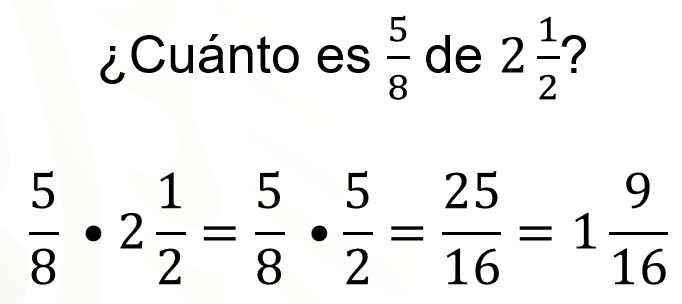
¿Este resultado resuelve el problema?, ¿qué más se tiene que hacer para resolverlo?
Ya sabemos que el agua requerida es de 1.8 litros y que la olla contiene un entero, 9 dieciseisavos de litro. Como estas 2 fracciones sólo son diferentes en su parte fraccionaria, podemos comparar estas partes y así deducir si falta o sobra agua.
La parte decimal punto 8 se puede expresar como la fracción decimal 8 décimos y se compara con la fracción nueve dieciseisavos. Se convierten estas fracciones en fracciones equivalentes con el mismo denominador; al hacerlo 64 ochentavos es mayor que 45 ochentavos, por lo tanto, también la fracción 8 décimos es mayor que nueve dieciseisavos.
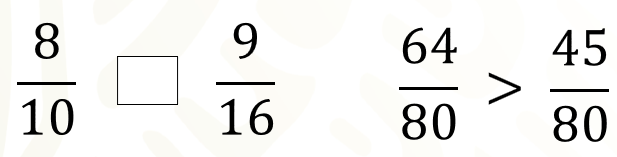
Entonces como 8 décimos es mayor que 9 dieciseisavos, el agua no alcanza; para saber cuánta agua falta, se realiza la sustracción del agua que se requiere menos el agua que contiene; ésta resta nos da un resultado de 19 ochentavos, por lo tanto, esta cantidad en litros es la que falta para cocinar la sopa.
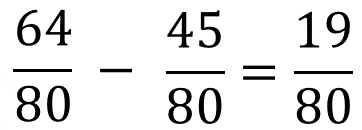
Resuelve otro problema.

¿Será importante saber cuánto es 3 cuartos de 4 enteros un medio? Si se van a hacer grupos de 3 cuartos de kilogramos, ¿esta acción se asemeja a una multiplicación o a una división?
Se tiene una existencia de 4 y medio kilogramos de café o bien 9 medios. Con dicha existencia se harán grupos, cada uno, de 3 cuartos de kilogramo. Lo que se quiere saber es la cantidad de paquetes que se pueden formar.
La acción de agrupar en cantidades iguales corresponde a una división. Por lo que, se ha planteado la división de fracciones, 9 medios entre 3 cuartos. Al resolver la división obtenemos 36 sextos que, convertido a enteros resulta 6. Entonces, la respuesta al problema del café es que se pueden envasar 6 paquetes con el café disponible.
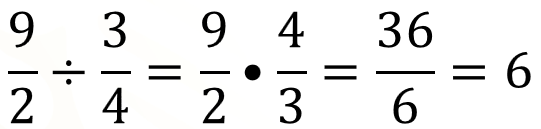
Ahora, revisaremos las potencias, en relación con la multiplicación, la división y la potencia de potencia, así como la raíz cuadrada de un número.
Una potencia se puede entender como la multiplicación repetida de un mismo factor. Así, por ejemplo, la potencia 2 al cubo, es la multiplicación del 2, tres veces. El resultado de esta potencia es 8, porque 2 por 2 por 2 es igual a 8.
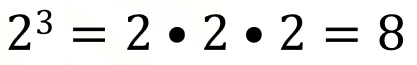
GIL:
El número que se multiplica se llama base, mientras que el número que indica las veces que aparece la base como factor se le llama exponente. Por lo tanto, en la potencia anterior, 2 es la base y 3 el exponente.

De manera inversa, podemos expresar una multiplicación de factores iguales como una potencia; en el ejemplo, la multiplicación de 3 por 3 es igual a 3 al cuadrado, que es igual a 9.
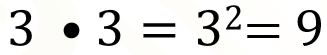
Para explicar lo que es una multiplicación de potencias desarrollemos cada una de las potencias que aparecen como factor en las multiplicaciones. En el primer caso se multiplica la potencia 3 al cubo por la potencia 3 al cuadrado, pero como has visto, cada potencia es una multiplicación de factores iguales, así que en el primer paréntesis está desarrollada la potencia 3 al cubo y en el segundo, se desarrolla 3 al cuadrado.
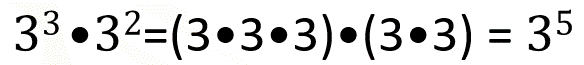
Al desarrollar las dos potencias tenemos que la base 3 aparece en total 5 veces como factor, así que, si expresamos esta multiplicación como potencia, tenemos 3 elevado al exponente 5. Observa que el exponente 5 de la potencia producto es igual a la suma de los exponentes 3 y 2 de las bases que se multiplican.
En todos los casos el exponente del resultado es igual a la suma de los exponentes de la base. Como esto sucede con todas las multiplicaciones de potencias de la misma base, entonces lo podemos generalizar. Se puede decir que, si se multiplican 2 o más potencias de la misma base, el resultado es la misma base y con el exponente que resulta de sumar los exponentes de esos factores. Esto, en forma algebraica se expresa como “x” a la “m” por “x” a la “n” es igual a “x”, a la “m más n”.
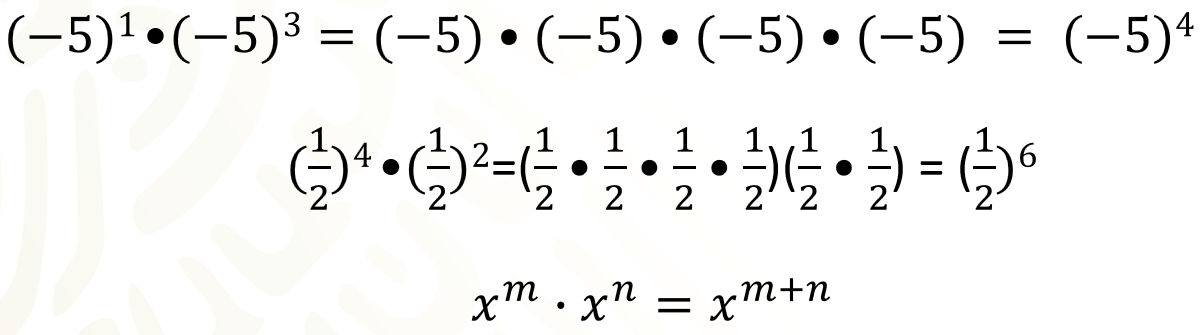
También la división de potencias de la misma base se puede generalizar.
En la primera división de potencias, 3 al exponente 4 entre 3 al cuadrado, se escribe en el numerador, 4 veces el 3 como factor y en el denominador, el 3 dos veces como factor. Enseguida, se realizan las dos divisiones de 3 entre 3, ya que en el denominador sólo aparece dos veces el 3, dichas divisiones dan como resultado 1. Luego, como al multiplicar por uno, el producto no se altera, entonces sólo queda el 3 multiplicado 2 veces, lo cual se puede expresar como 3 al cuadrado. Entonces, el resultado de 3 al exponente 4 entre tres al cuadrado es 3 al cuadrado. Debe observarse que este resultado se puede obtener directamente escribiendo la misma base y restando los exponentes.
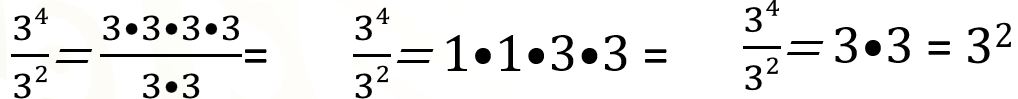
Ahora bien, en el segundo ejemplo se han simplificado los factores con líneas rojas.
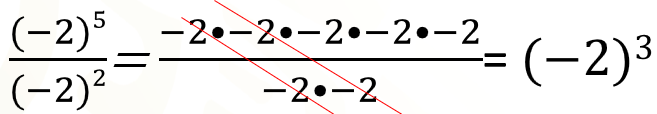
Por lo que sólo queda 3 veces el 2 negativo como factor, el cual expresado en potencia es 2 negativo al cubo. La acción de eliminar números iguales en el dividendo y el divisor, como se hizo con las líneas rojas, tiene su justificación en que al dividir números iguales resulta 1, y que, al multiplicar por 1, resulta el mismo número.
Entonces, se puede decir que, el resultado de dividir potencias de la misma base es una potencia con la misma base y exponente que resulta de restar los exponentes del dividendo menos el del divisor, o bien que “x” a la “m” entre “x” a la “n” es igual a “x”, a la “m” menos “n”.
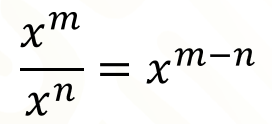
Una potencia de potencia quiere decir que una base está elevada a un exponente y que, a la vez, esta potencia está elevada a otro exponente.
En la primera operación, se ha desarrollado la potencia dentro del paréntesis, que corresponde a 3 al cuadrado, por eso aparece el 3 dos veces como factor, pero como este desarrollo está elevado al cubo, se han escrito 3 veces entre paréntesis, es decir, como factor.
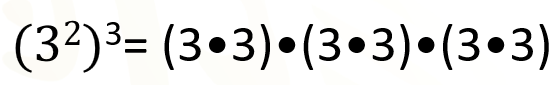
Como el 3 siempre aparece como factor, entonces esto se puede escribir sin los paréntesis; al hacerlo, se percibe que el 3 aparece 6 veces como factor, que se puede escribir como 3 al exponente 6.
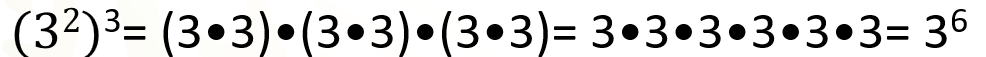
Lo mismo sucede con el segundo ejemplo.
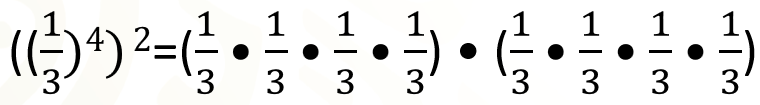
Un tercio; primero se encuentra 4 veces como factor y este desarrollo se repite dos veces, entonces, como todos son factores, esto se puede expresar como un tercio al exponente 8. ¿Cuál es la operación que se realiza con los exponentes para obtener directamente el resultado?
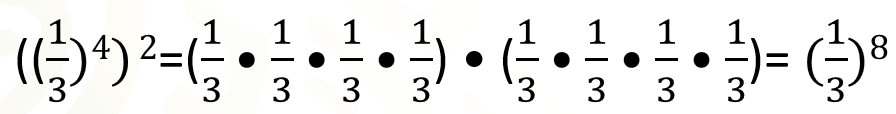
Se realiza una multiplicación de exponentes, ya que, en el primer ejemplo 3 por 2 son 6 y en el segundo, 4 por 2 es igual a 8. En resumen, el resultado de una potencia de potencia, es la misma base elevada al exponente que resulta de multiplicar los exponentes o bien “x” a la “m”, a la “n”, es igual a “x”, a la “m” por “n”.
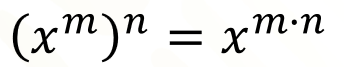
Aborda ahora algunos aspectos de la raíz cuadrada. La raíz cuadrada de números que no son cuadrados perfectos constituye una aproximación. Así, si se quiere calcular la medida de los lados de un cuadrado con 40 centímetros cuadrados de área, una manera de hacerlo es determinar la raíz cuadrada de 40. Como 40 no es un número cuadrado perfecto, entonces, podemos calcular su raíz cuadrada mediante aproximaciones. Observa que resultado estará entre 6 y 7, ya que 6 por 6 es igual a 36 y 7 por 7 es igual a 49.
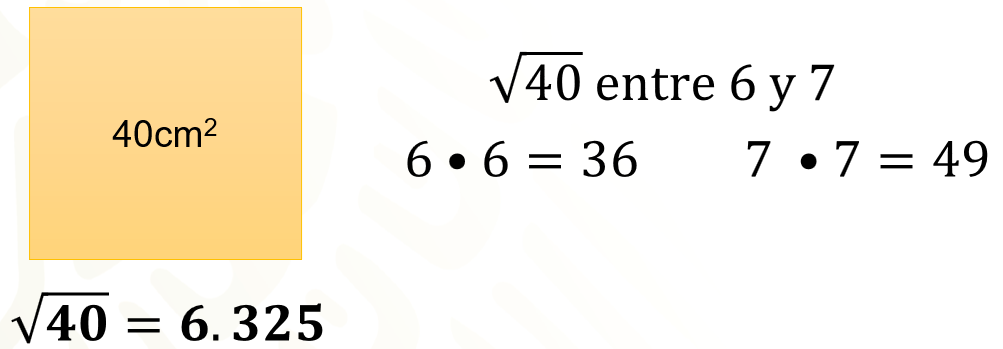
Al intentar con 6 punto 5, al multiplicarlo por sí mismo, el resultado es mayor que 40.
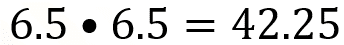
Ahora con 6.25, al multiplicarlo por sí mismo es un número menor que 40.
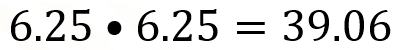
Con 6.3 se obtiene un número menor y muy cercano a 40.
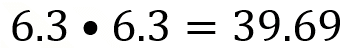
Con el 6.4 nuevamente se pasa.
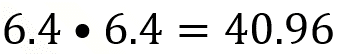
Si realizas el cálculo con tu calculadora, ¿qué número obtienes?
Sea cual sea el resultado que obtuviste, también será una aproximación, mejor, de la raíz cuadrada de 40, pero no será exacta.
El reto de hoy:
Reflexiona sobre la importancia que conlleva el hecho de estudiar estos temas.
Conocimientos de las operaciones, como los que revisaste el día de hoy, son muy importantes para resolver problemas de la vida cotidiana, pero también son las bases para que continúes tus estudios.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas