La media aritmética
Aprendizaje Esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana) y el rango de un conjunto de datos y decide cual de ellas conviene más en el análisis de los datos en cuestión.
Énfasis: identificar los diferentes usos de la media: reparto equitativo, mejor estimación de la medida real de un objeto y como representante de un conjunto de datos.
¿Qué vamos a aprender?
En esta sesión trabajarás un tema relacionado con las medidas de tendencia central, en específico trabajarás con la media aritmética, e identificarás los diferentes usos que tiene, como reparto equitativo, la estimación real de la medida de un objeto y como representante de un conjunto de datos.
Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, sacapuntas y regla. Así como tu libro de texto de la asignatura.
En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.
¿Qué vamos a hacer?
¿Qué te parece si para comenzar analizas la siguiente situación?
Se te sugiere poner atención y tomar nota de la información más relevante.
Hoy en día las redes sociales han tenido un gran impacto, ya que con tanta información que hay en internet, ha surgido la necesidad de crearla, compartirla, conectarte y difundirla con otras personas que conoces, como por ejemplo con tus amigos, familiares, compañeros de clase, o con personas que comparten tus mismos intereses.
Julio es un estudiante que utiliza con mucha frecuencia sus redes sociales, la que mayormente utiliza es Facebook, por lo que su hermana le preguntó ¿Cuántas horas a la semana navega en Facebook?
Como en ese momento no tenía idea de las horas a la semana que utiliza esta red social, realizó un registro por cada uno de los días de la semana y al finalizar contabilizó que utiliza esta red social durante 28 horas por semana, por lo que le surgió la siguiente inquietud: ¿Será demasiado tiempo el que ocupa en Facebook?
Para tener un mejor panorama del tiempo decidió realizar la misma pregunta que le hizo su hermana a todos los integrantes de su familia y a sus amigos más cercanos obteniendo los siguientes resultados:
8, 2, 30, 21, 25, 20, 24, 11, 5, 22, 7, 26, 15, 10, 18, 6, 5, 19, 12, 16, 14, 32, 5, 35.
¿Cuántas horas en promedio navegan en Facebook sus amigos y la familia de Julio? ¿Ya sabes cómo darle solución a esta situación?
Julio debe obtener la media aritmética también llamada promedio, del conjunto de datos que obtuvo de las respuestas que le proporcionaron sus amigos y familiares.
Como sabes la media aritmética es el valor característico de un conjunto de datos, que se obtiene al sumar todos los datos y dividir el resultado entre el total de los mismos.

Seguramente, tú en casa ya realizaste las operaciones necesarias para obtener las horas promedio, hay que revisar cual es el procedimiento.
Para darle solución a esta situación lo primero que deberás realizar es ordenar de menor a mayor los datos que obtuvo Julio, cabe mencionar que para obtener la media aritmética no es necesario ordenar los datos, pero lo harás para tener una mejor organización de los mismos, esto te ayudará a entender mucho más rápido la información.
Ahora realizarás la suma correspondiente de todos los datos, lo cual te dará como resultado 388.
¿Entre qué número debes dividir el resultado anterior para obtener la media?
Así es, entre 24, ya que es la cantidad total de los datos que se obtuvieron.
Por lo tanto, la media aritmética es 388 entre 24, aproximadamente 16.1666 periódico, redondeando este resultado la media sería igual a 16.2.

Por lo que se puede decir que en promedio las horas a la semana que utilizan Facebook sus amigos y familiares de Julio son 16.2 horas.
Así, Julio ya podrá saber si es demasiado tiempo el que ocupa en esta red social, él contabilizó que a la semana utiliza 28 horas para navegar en esta red social, si el promedio que se obtuvo de sus familiares y amigos fue de 16.2 horas, se puede decir que la cantidad de horas que utiliza Julio para navegar en Facebook, está muy por arriba del promedio de las horas que navegan sus amigos y familiares, por lo que Julio debería tomar la decisión de reducir el número de horas a la semana que navega en esta red social.
En la situación anterior, pudiste observar el procedimiento que se debe seguir para obtener la media aritmética en un conjunto de datos.

La media aritmética es interpretada como reparto equitativo cuando se desea distribuir, en partes iguales la suma de las cantidades que indican los datos. Para tener una mejor comprensión de esta información analiza la siguiente situación y ve un ejemplo del uso de la media aritmética como reparto equitativo. Se te sugiere poner atención y tomar nota de la información más relevante.
Un grupo de amigos decidió reunirse en la casa de su amiga Fátima para celebrar el día de la amistad e intercambiar tarjetas con diferentes frases de amistad. Francisco hizo 8 tarjetas; Laura, 5; Verónica, 4, Miguel 6 paletas, Toño 7; Luz 2; Guadalupe 8 y a Fátima no le dio tiempo de preparar sus tarjetas debido a que estuvo preparando una pequeña comida para sorprender a sus amigos en el festejo. Al ver esta situación Verónica propuso que compartieran las paletas de manera equitativa.
En casa se te invita a escribir en tu cuaderno las siguientes preguntas para reflexionar:
- ¿Para obtener la media aritmética se tendrá que tomar en cuenta al número 0, como un dato a considerar?
- ¿Cuántas tarjetas le tocarán a cada uno?
Ahora hay que dar solución a esta situación, lo primero que harás es ordenar de menor a mayor los datos, esto para tener una mejor organización.
Los datos son: 8, 5, 4, 6, 7, 2, 8, 0, ordénalos de menor a mayor por lo que ahora el orden será: 0, 2, 4, 5, 6, 7, 8 y 8.
Listo ya se tienen los datos ordenados, ahora hay que obtener la media aritmética.
Realizarás la suma correspondiente de todos los datos, 0 + 2 + 4 + 5 + 6 + 7 + 8 + 8 lo que te da como resultado 40.
Como puedes ver y para dar respuesta a la pregunta si el cero debe considerarse, esto es correcto, si lo tienes que tomar en cuenta ya que si no lo hicieras la media aritmética se vería afectada y la repartición no sería equitativa.
¿Entonces, entre qué número debes dividir entre 7 u 8?
La respuesta es, entre 8, ya que es la cantidad de amigos, sin importar que Fátima no puso ninguna tarjeta, por eso se considera al número cero, porque ese valor representa a Fátima.
Por lo tanto, 40 entre 8 es igual a 5, la media aritmética es igual a 5.

Entonces a cada uno les deberá tocar 5 tarjetas.
Eso significa que cuando se realiza un reparto de manera equitativa, el dato o cantidad a repartir corresponde al valor de la media aritmética.
Ahora, pon atención al siguiente video, para ahondar más sobre la representación de la media como reparto equitativo. Toma nota de la información más relevante.
- Datos estadísticos.
https://www.youtube.com/watch?v=QRIkOY1Tr6s
Revisa del tiempo 00:37 al 03:40.
En los ejemplos que observaste en el video, se vio cómo se emplea a la media aritmética en otro tipo de contextos.
Ahora revisa otra situación.
Luis tiene una pequeña empresa, la cual ofrece servicios de jardinería a domicilios particulares, empresas, parques e iglesias, para poder cubrir la demanda del trabajo cuenta con 8 empleados, los cuales obtienen su salario de acuerdo con las horas que trabajan, ya que no tienen un horario fijo, por lo que Luis debe llevar un registro por día para saber cuánto es lo que tiene que pagar a la semana, a cada uno.
El lunes registró lo que ganó cada empleado de acuerdo a las horas que trabajaron, el primer empleado ganó 140 pesos, el segundo 120 pesos, el tercero 100 pesos, el cuarto 100 pesos, el quinto empleado obtuvo una ganancia de 80 pesos, el sexto gano 80 pesos, el séptimo gano 180 pesos y el último 110 pesos.
Se te invita a escribir en tu cuaderno la siguiente pregunta a reflexionar:
¿Cuánto cobran los trabajadores de Luis en promedio?
Que te parece si se le da solución a esta situación.
¿Qué es lo primero que debes realizar para obtener el promedio o la media?
Lo primero que harás será sumar todos los datos.
Ahora realizarás la suma correspondiente de todos los datos, 80 + 80 + 100 + 100 + 110 + 120 + 140 + 180, te da como resultado 730, ahora para obtener la media aritmética, divides la suma entre 8, ya que es la cantidad de empleados de Luis.
Por lo tanto, la media aritmética es igual a 91.25, es decir, en promedio el salario de los empleados de Luis el día lunes fue de $91.25.
Entonces cada uno de los empleados de Luis en promedio ganó $91.25 ese día.
En esta situación puedes observar que la media aritmética se usó para estimar un valor que es representativo, es decir, que los datos que se obtuvieron fueron a través de diversas mediciones de ese valor, que en este caso fue el salario por día de cada uno de los empleados de acuerdo al número de horas que trabajaron.
Ahora, pon atención al siguiente video en donde se muestran varios ejemplos, en los que se usa la media, para la estimación de un valor representativo y toma nota de la información más relevante. - Una misma medida, diferentes significados.
https://www.youtube.com/watch?v=k6Ki19MmBcc
Revisa del tiempo 00:55 al 04:28.
Hasta el momento has analizado la media aritmética como reparto equitativo y para estimar un valor a partir de un conjunto de datos numéricos.
Ahora, vas a analizar un caso en el que la media se usa como dato representativo de un conjunto de valores, esto sucede cuando la media es muy cercana a la mayoría de valores, es decir, se encuentra más o menos al centro del conjunto de datos.
Marco es un experto en nutrición y trabaja en un hospital en donde ofrece consultas en nutrición dando orientaciones a las personas, creando planes alimenticios saludables adecuados a las necesidades de salud y actividades físicas de cada uno de sus pacientes.
Marco seleccionó a 10 de sus pacientes para que integrarán un programa nuevo en nutrición, cada uno de los participantes tiene problemas de obesidad, el programa consiste en que estos participantes pierdan masa a través de una dieta saludable y a base de ejercicios específicos. Marco realizó la siguiente tabla donde se muestra la masa en kilogramos de cada una de las personas que se sometieron a dicho programa.
Se te invita tomar nota en tu cuaderno de la siguiente tabla y de la pregunta a reflexionar.
¿Cuál es la masa promedio en kilogramos de los integrantes del programa de nutrición?
Revisa la información que contiene la tabla.
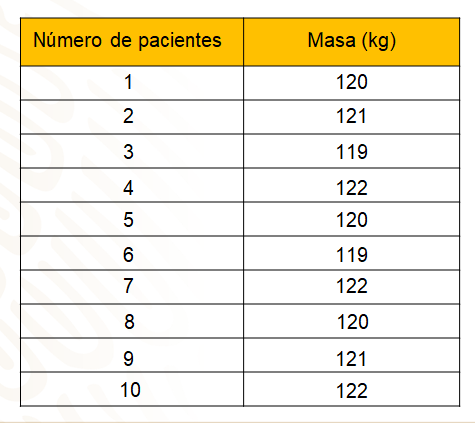
La tabla tiene dos columnas, una corresponde al número del paciente, la segunda corresponde a la masa en kilogramos, de cada uno. En la primera fila se colocaron los títulos de las columnas, el primero es “número de pacientes” y el segundo título es “peso en kilogramos”. En cada fila de la primera columna se registró el número del paciente: 1, 2, 3, 4, 5 ,6 ,7 ,8 ,9 y 10. En cada fila de la segunda columna se registró el peso en kilogramos de cada uno de los pacientes: 120, 121, 119, 122, 120, 119, 122, 120, 121 y 122.
Para darle solución a esta situación lo primero que debes realizar es ordenar de menor a mayor las masas de los pacientes de Marco, esto para tener una mejor organización de los datos, para entender más rápidamente la información.
Después realizas la suma correspondiente de todos los datos, en donde te da como resultado 1,206.
¿Entre qué número deberás dividirlo?
Así es, entre 10, ya que es la cantidad total de pacientes que tiene el programa de nutrición.
Por lo tanto, la media aritmética es aproximadamente = 120.6.

Como puedes ver, al ordenar los valores del conjunto, observas que la media se encuentra al centro de éstos, por eso se considera un dato representativo.

Entonces ya puedes darle respuesta a la pregunta: ¿Cuál es la masa promedio en kilogramos de los integrantes del programa de nutrición?
La masa promedio es de 120.6 kilogramos.
Si Marco tuviera que agregar a otras tres personas al programa de nutrición, considerando la masa promedio, ¿qué masa deberá considerar para poderlos ingresar al programa de nutrición?
Estas tres personas deberán tener una masa cercana a 120.6 kilogramos para poder participar en el programa de nutrición.
Ahora regresando, a la primera situación que se te planteó para obtener la media aritmética, que fue la de Julio que es un estudiante que utiliza con mucha frecuencia sus redes sociales, en donde se te solicitó encontrar cuántas horas en promedio navegan en Facebook sus amigos y la familia de Julio.

Recuerda que obtuviste que el promedio de horas que navegan sus familiares y amigos fue aproximadamente de 16.1666 periódico, redondeando este resultado la media sería igual a 16.2.
En esta situación la media se usó ¿cómo reparto equitativo, como mejor estimación de la medida real de un objeto o como representante de un conjunto de datos?
La respuesta es, como mejor estimación, ya que se realizaron diversas mediciones de las horas de navegación en la red social Facebook.
Cómo te puedes dar cuenta la media aritmética se encuentran presente en varias situaciones cotidianas, y en esta sesión identificaste los diferentes usos de la media: como reparto equitativo, que como viste puedes identificar este tipo de situaciones cuando se desea distribuir en partes iguales la suma de las cantidades que indican los datos, otro de los usos de la media es como mejor estimación de la medida real de un objeto, que como viste puedes identificar este tipo de situaciones cuando los datos se obtienen a través de diversas mediciones de ese mismo valor, por tanto en esas situaciones la media aritmética se considera como la mejor estimación real del objeto y el último uso que viste de la media es como representante de un conjunto de datos, este tipo de situaciones las puedes identificar cuando no hay algún dato que tenga un valor extremo muy diferente a los demás y el promedio es lo más cercano posible a todos los datos.
El reto de hoy:
Revisa en tu libro de texto el tema que estudiaste en esta sesión y realiza las actividades que ahí se te sugieren.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas