Juguemos a las fuerzas
Aprendizaje esperado: describe, representa y experimenta la fuerza como la interacción entre objetos y reconoce distintos tipos de fuerza.
Énfasis: describir el cambio de dirección de objetos.
¿Qué vamos a aprender?
Conocerás qué es una interacción y cuáles son los efectos de las fuerzas en los objetos.
Las fuerzas son interacciones recíprocas entre dos o más objetos, las cuales pueden ser a distancia o por contacto, estas interacciones dan origen a cambios en el movimiento. Una fuerza puede generar movimiento, esta fuerza tendrá un punto de aplicación que depende del observador o del sistema de referencia; a cualquier objeto que se mueve se le llama móvil y, dependiendo de la fuerza que se aplique, el móvil tendrá una cierta aceleración y velocidad. Los móviles describen una trayectoria que tiene una cierta distancia, además de que tienen un desplazamiento que depende de su posición inicial y final.
Cuando dos objetos están en contacto y, sus dos superficies interactúan produciendo dos fuerzas en sentido contrario, se produce fricción. La fricción es una fuerza que, más tarde que temprano, va a hacer que los objetos se detengan. También se puede producir que alguno de los objetos, o ambos, se desgasten, como las suelas de nuestros zapatos o las llantas de los automóviles.
Existen muchos tipos de fuerzas, por ejemplo:
- La fuerza de gravedad
- La fuerza magnética
- La fuerza entre cargas eléctricas
- La fuerza eólica
- La fuerza hidráulica
- La fuerza de fricción
Para representar a una fuerza, se puede usar un vector, y este se representa mediante una flecha.
La punta o cabeza de la flecha indica hacia donde se aplica la fuerza, es decir la dirección, y el otro extremo indica el punto de aplicación de la fuerza.
¿Qué hacemos?
Observa el siguiente video para conocer más sobre los elementos de un vector.
Fuerzas en acción.
Como observaste en el video, para poder representar el vector de una fuerza se debe conocer:
- La magnitud
- La dirección
- El sentido
- El punto de aplicación
- La escala.
Un vector es un segmento de recta con punta de flecha, en pocas palabras una flecha
Magnitud (M). Es la fuerza que se aplica sobre un objeto y se mide en Newtons, cuya equivalencia es:
1 Newton = 1 Kg/s2
¿Qué significa esto?
Imagina que tienes un objeto de un kilogramo y está sobre una superficie tan lisa que puedes despreciar la fuerza de fricción. Si se aplica una fuerza de un newton entonces el objeto de un kilogramo aumentará su velocidad 1m/s cada segundo durante la aplicación de la fuerza. Así si parte del reposo, después de un segundo su velocidad será 1m/s, con otro segundo más irá a 2m/s y así mientras se aplique una fuerza de un newton.
20N = 20kg x m /s2
La unidad de medida de fuerza es el newton que se representa con el símbolo: N, esta unidad fue nombrada así en reconocimiento al científico Isaac Newton por sus aportaciones a la física.
Dirección (D). Nos indica de donde proviene y hacia dónde se aplica la fuerza, este movimiento puede representarse con los grados de un círculo o una Rosa de los Vientos (brújula).
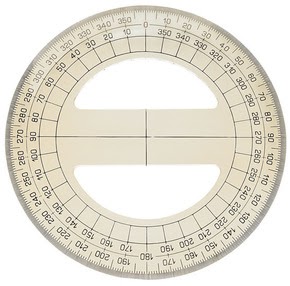

Una fuerza puede desplazarse hacia cualquiera de los grados de un círculo, por ejemplo, a 45º, a 90º, a 120º, etc. Siempre se miden los grados en sentido contrario de las manecillas del reloj.
Sentido (S). Es el lugar hacia donde se dirige la fuerza.
Punto de Aplicación (PA). Es el punto representativo sobre el cual se aplica la fuerza
Escala (Esc). Es la relación de proporción entre las dimensiones reales de un objeto y las de un dibujo.
Las escalas sirven para representar algún objeto cuando éste es muy grande o pequeño, y no se pueden dibujar en medidas reales. Por ejemplo: no se podría dibujar un carro de tamaño real en una hoja porque no cabe, por lo que se usa una proporción.
Para saber cómo se aplica una fuerza sobre un objeto y cómo se representa con un vector, observa el siguiente ejemplo:
M: 15 N
D: Desde el centro hacia 180º
S: 180º
PA: EL BALÓN
Esc.: 1cm = 5N (cada segmento equivale a 5N)
Sistema de fuerzas.
Un Sistema de fuerzas se produce cuando se aplican dos o más fuerzas sobre un mismo objeto.
Existen varios tipos de sistemas de fuerzas: colineales, concurrentes con el mismo sentido o con sentido inverso, y con fuerzas paralelas.
Sistema de fuerzas colineales. Son aquellas que se ejercen sobre un objeto, en la misma dirección, pero no necesariamente en el mismo sentido en línea recta.
Ejemplo:
Si empujas una mesa mientras otra persona tira de ella, y entre los dos la mueven en dirección de 135°, ¿cómo se representaría con un vector del sistema fuerza?
Fuerza Resultante de 25 N
(F1= 10N) + (F2 =15N) =25 N
Debido a que las fuerzas aplicadas están en la misma dirección y sentido, entonces este esfuerzo para mover la mesa simplemente se suma y se obtiene una fuerza resultante.
Por lo tanto, se suman las fuerzas y se traza el vector resultante.
Resultante
M: 25 N
D: Desde el centro o vértice hacia 45º
S: 45º
PA: La mesa
Esc.: 1cm = 5N (por lo que el vector va a medir 5 cm)
Sistema de fuerzas concurrentes con la misma dirección y distinto sentido. Las fuerzas se aplican sobre el mismo objeto, tienen la misma dirección, pero diferente sentido, es decir, se oponen.
Continuando con el ejemplo anterior de la mesa:
Ahora, una persona aplica una fuerza empujando la mesa por un extremo, y la otra persona realiza la misma acción, pero por el extremo contrario.
¿Hacia qué lado se moverá?
¿Cómo se representaría en un vector?
(F1= 15N) – (F210N) = 5N
Fuerza Resultante

5 N, 180º
Debido a que las fuerzas aplicadas por las dos personas sobre el mismo objeto tienen la misma dirección, pero sentidos opuestos, entonces este esfuerzo de cada uno para mover la mesa en diferentes sentidos se resta y se obtiene una fuerza resultante hacia el sentido y dirección de la fuerza más grande. En este caso, la primera persona empujó con más fuerza.
Resultante
M= 5 N
D: desde el centro hacia 180º
S: 180º
PA: La mesa
Esc.: 1 cm = 1 N (por lo que el vector va a medir 5 cm)
Sistema de fuerzas concurrentes con distinta dirección y distinto sentido. Son aquellas fuerzas que se aplican sobre el mismo objeto, pero con distinta dirección y sentido.
Observa el ejemplo:
(Dos personas tiran de la mesa hacia una diferente dirección y sentido)
Fuerza Resultante
14 N, 180°
En este caso la resultante se obtiene por el método del paralelogramo, que consiste en trazar líneas imaginarias paralelas que, al unirse, forman un vértice, entonces la resultante se traza a partir del centro de los ejes hacia el vértice que se forma con las líneas paralelas imaginarias. Se mide la distancia del vector con la regla (14 cm en este caso), y la escala indica a cuanto equivale, 1cm = 1N. Por lo que la resultante será de 14 N, y la dirección se obtiene midiendo con el transportador el ángulo desde la intersección de los ejes, hasta donde llega la resultante.
Resultante
M = 14 N
D: desde el centro o vértice hacia 135º
S: 135º
PA: La mesa
Esc.: 1 cm = 1 N (por lo que el vector va a medir 14 cm)
Cuando son más de tres vectores, se traza un vector a continuación del otro, uniendo el inicio del primer vector con el final del último vector. Se mide la distancia, y la escala indica a cuánto equivale. Este es el método del polígono.
Esto explica porque al aplicar dos fuerzas hacia diferentes direcciones, el objeto termina moviéndose en otra dirección.
Sistema de fuerzas paralelas. Son aquellas fuerzas que se ejercen sobre el mismo objeto, con la misma dirección y en el mismo sentido, una a lado de la otra.
Observa el ejemplo:
(Dos personas tiran de la mesa hacia la misma dirección y en el mismo sentido).
Resultante
M: 25 N
D: desde el centro o vértice hacia 135º
S: 135º
P.A: la mesa
Esc: 1cm= 5 N (por lo que el vector medirá 5 cm)
En este caso, despreciando la fricción entre la mesa y el piso, la resultante se obtiene sumando las fuerzas que se aplican a la mesa.
Existen varios tipos de Sistemas de fuerzas vectoriales y cuando se ejercen varias fuerzas sobre el mismo cuerpo, se puede conocer o predecir el efecto de dichas fuerzas, sumándolas para obtener la resultante. También se pueden usar métodos gráficos, como el método del polígono y el método del paralelogramo, que fue el que se mostró en uno de los ejemplos.
Observa el siguiente video en donde se explica cómo obtener la resultante en un sistema de fuerzas, por el método del polígono.
Suma de vectores.
https://youtu.be/YzXoxs-0uLA
Con el método del paralelogramo se puede saber la magnitud de la fuerza que se requiere para poder levantar un objeto, por ejemplo: cuando dos familiares adultos juegan con un niño, lo toman cada uno de una mano y lo levantan al mismo tiempo.
Método del paralelogramo
Por el método del polígono, se puede saber cuánta fuerza se requiere para subir una cama a un primer piso, cuando re realiza una mudanza.
En resumen.
Una fuerza genera movimiento o deformación. Las fuerzas se representan con un vector, cuando se aplican dos o más fuerzas, se les llama Sistemas de fuerzas vectoriales. Existen diferentes Sistemas de fuerzas vectoriales: Sistema de fuerzas colineales, Sistema de fuerzas concurrentes con el mismo sentido y con sentido inverso, Sistema vectorial de fuerzas paralelas.
Se puede conocer la resultante de un cuerpo al que se le aplican diferentes fuerzas, usando métodos gráficos como el método del paralelogramo y el método del polígono.
El reto de hoy:
Para comprobar lo que has aprendido, describe e ilustra un ejemplo de cada uno de los tipos de sistemas vectoriales con situaciones que observes en tu entorno y elabora el trazo de los sistemas vectoriales de las fuerzas que se aplican en cada caso. Recuerda que puedes consultar tu libro de texto en caso de que tengas dudas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas











