Jerarquía de operaciones
Aprendizaje esperado: determina y usa la jerarquía de operaciones y los paréntesis en operaciones con números naturales, enteros y decimales (para multiplicación y división, solo números positivos).
Énfasis: aplicar la jerarquía de operaciones usando operaciones básicas.
¿Qué vamos a aprender?
En dos sesiones, estudiarás aspectos esenciales de la jerarquía de operaciones; en esta lección conocerás el orden en que deben realizarse las operaciones, y en la siguiente lección aprenderás a utilizar los signos de agrupación.
¿Qué hacemos?
Para iniciar te planteamos la siguiente situación: En una red social, había un reto matemático y una acalorada discusión sobre cuál era el resultado correcto. Los usuarios de la red social, no se ponían de acuerdo. Cada quien argumentaba su procedimiento y resultado, pues creían tener la razón. El reto era resolver la expresión aritmética: 5 + 10 x 3.
Las opiniones se dividían en dos, había quienes decían que el resultado correcto era 45 y, la otra parte, que era 35. ¿A qué resultado llegas tú? Anótalo y lo verificaremos después.
- Redes sociales
https://youtu.be/fBWimz2jKZY
Quienes decían que el resultado correcto era 45, sumaron 5 más 10, que resulta 15, y luego multiplicaron ese resultado por 3, lo que da 45.
Por otra parte, quienes decían que el resultado correcto era 35, primero multiplicaron 10 por 3 que resulta 30, y luego sumaron el 5, lo que da 35. ¿Quiénes tienen la razón?
Para llegar a un resultado correcto. Es necesario establecer un orden, deben existir convenciones, acuerdos o reglas que nos ayuden a encontrar un resultado en el que coincidamos. En la vida cotidiana hay muchos aspectos en los que se siguen reglas o acuerdos. Eso nos permite comunicar ideas y emociones de forma eficaz.
En lecciones pasadas la música fue de gran ayuda para comprender aspectos matemáticos. Dando continuidad al ejemplo, en la música, el orden en el que se acomodan las notas genera una idea musical única. Si el orden se cambia, la melodía será distinta. Inclusive, hay signos muy pequeños que cambian el sonido asociado a las notas, uno de ellos es el bemol.
Existe una canción popular que se llama Martinillo, que nos servirá de ejemplo. Para ello, observa el siguiente video: - Martinillo do mayor
https://youtu.be/4JQw6bDX8fk
En el video, la campana se mueve de acuerdo con el orden en el que el piano toca esas notas, así que si fuera un orden diferente la melodía sería distinta. Algo similar sucede en las matemáticas, si cambiamos el orden para resolver las operaciones, puede cambiar el resultado.
La letra de la canción dice: Martinillo, Martinillo ¿dónde estás?, ¿dónde estás? Toca la campana, toca la campana. ¡Din, don, dan! ¡Din, don, dan! Es alegre, pero si agregamos un bemol a dos notas: Mi y La podemos provocar un cambio radical. Obsérvalo en el siguiente video: - Martinillo do menor
https://youtu.be/U0gfv5P7T7w
Ahora el sonido es melancólico, en lugar de alegre. Las notas fueron las mismas, y el orden también. La diferencia fueron los pequeños bemoles. En las matemáticas hay signos que se incluyen en los enunciados matemáticos, para cambiar el orden de resolución de las operaciones, lo que también puede cambiar el resultado. Por eso es muy importante conocer las reglas y los signos que pueden tener ese efecto. Ya que existe un orden para resolver las operaciones de un enunciado numérico. En otras palabras, hay operaciones que se hacen antes que otras, para llegar a un resultado convencional correcto.
A través de la jerarquía de operaciones, comprenderás el orden para resolver cualquier expresión aritmética y saber la respuesta correcta a situaciones; como el reto en redes sociales. Para conocerla, observa el siguiente video: - Clip 2. Jerarquía de operaciones
Del minuto: 00:00 a 01:26
https://youtu.be/ozqKapcHyvw
Jerarquía es un orden, en este caso, el orden en que deberán resolver las operaciones de un enunciado numérico. Así, pues, existe un orden de ejecución.
En el primer nivel del orden de ejecución están las operaciones agrupadas, a través de los paréntesis, los corchetes y las llaves. Aprenderás más sobre estos signos de agrupación en la siguiente lección.
En el segundo nivel del orden de ejecución, se operan los exponentes y raíces. En el siguiente nivel del orden de ejecución están las multiplicaciones y divisiones. Nota que están juntas y por consiguiente, tienen la misma jerarquía: multiplicaciones y divisiones.
En el último nivel del orden de ejecución, se encuentran las sumas y las restas. Esto significa que son las últimas operaciones que se realizan, y están en el mismo nivel de jerarquía.
Cuando en un enunciado numérico solo hay operaciones de la misma jerarquía, es decir, que se encuentran en el mismo nivel de ejecución. Simplemente se realizan de izquierda a derecha.
Con esta información ya puedes definir cuál es el resultado correcto en el reto matemático, de las redes sociales: El enunciado matemático es: 5 + 10 x 3
Hay dos operaciones con orden de ejecución distinto según la jerarquía de operaciones.
Las multiplicaciones y divisiones se resuelven primero que las sumas y las restas.
Entonces, primero resolvemos la multiplicación 10 por 3, lo que resulta: 30.
Después resolvemos la suma, por lo que 30 más 5, nos da 35.
Un error común, es resolver las operaciones siempre de izquierda a derecha, sin considerar que hay operaciones con diferentes jerarquías. En este caso, como hay operaciones con distinta jerarquía en este enunciado numérico, debemos resolverlas en el orden de ejecución correcto. Recuerda resolver primero multiplicaciones y divisiones, luego sumas y restas.
Ahora observa atención al siguiente video y trata de identificar cuál de los dos personajes tiene la razón en el reto que se plantea. - El orden de las operaciones
Matemáticas, Primer grado, Bloque: 1
https://youtu.be/gsNA8uRd798
Emma llegó al resultado correcto, porque siguió la jerarquía de las operaciones.
Ahora te proponemos Consolidar este conocimiento: ¡Jugando!
Usaremos una ruleta digital en la que están escritos diferentes enunciados numéricos. La haremos girar y ganarás un punto si tu respuesta es correcta.
¡Comenzamos, vamos a hacer girar la ruleta! - Ruleta v 1
https://youtu.be/rt_MQFBb0DU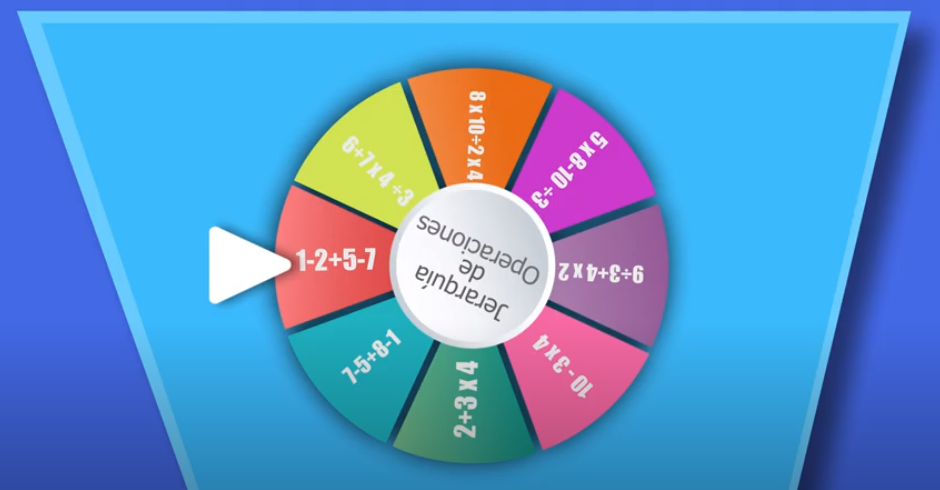
El resultado es 3 negativo. En este enunciado numérico todas las operaciones tienen la misma jerarquía, así que, simplemente se resuelve de izquierda a derecha
Para resolver el enunciado numérico:
1 – 2 + 5 – 7, se comienza de izquierda a derecha con 1 – 2 igual a 1 negativo, ahora al 1 negativo se le suma 5, lo que resulta 4. Finalmente, al 4 se le resta 7 lo que me da como resultado 3.
Giremos la ruleta otra vez. - Ruleta v 2
https://youtu.be/v15VNIfbSAE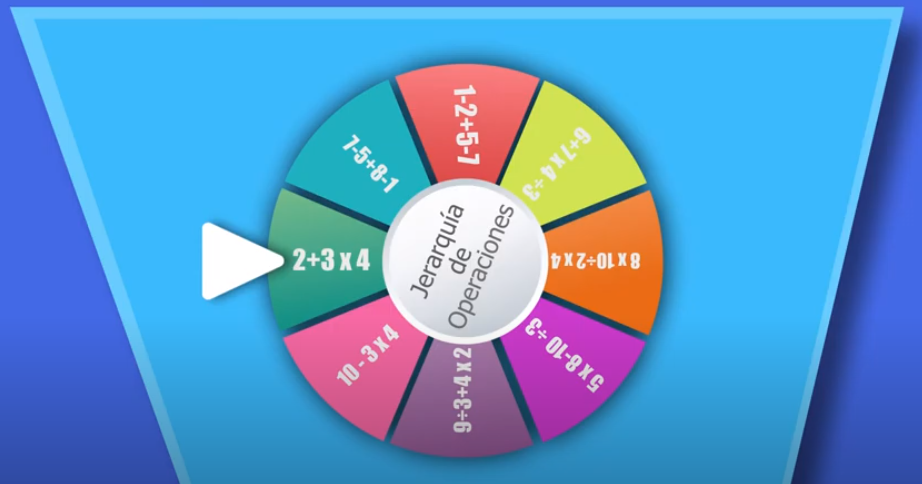
En este caso hay operaciones con diferente nivel de ejecución. El resultado correcto es 14.
En el enunciado:
2 + 3 x 4 hay una multiplicación, que se debe resolver antes que la suma:
3 x 4 = 12
Ahora sí se puede resolver la suma:
2 + 12 = 14 - Ruleta v 3
https://youtu.be/jwMVaoKEEQQ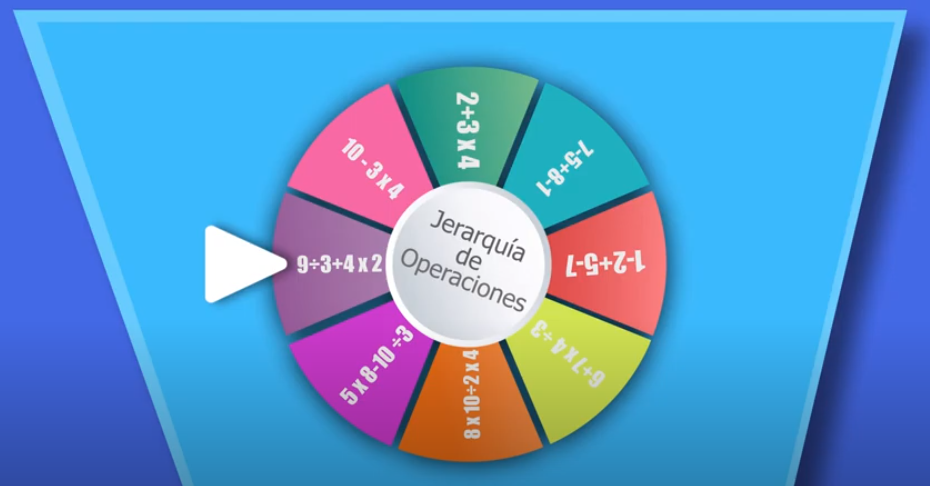
En este caso hay dos operaciones con el mismo nivel de ejecución, la división y la multiplicación. Pero también hay una suma que tiene un nivel distinto. El resultado correcto es: 11.
En el enunciado:
9/3 + 4 x 2, primero se resuelve la división 9/3=3, ahora la multiplicación 4 x 2=8. Finalmente se suman 3+8=11. - Ruleta v 4
https://youtu.be/ElrtiFKcYKA
En este caso hay operaciones con el mismo nivel de ejecución, la división y la multiplicación. Así que se resuelven de izquierda a derecha. El resultado correcto es: 160.
En el enunciado:
8 x 10: 2 x 4 primero se resuelve la multiplicación:
8 x 10=80, ahora divido entre 2:
80:2=40. Finalmente se multiplica por 4,
quedando: 160.
En la siguiente lección se abordará el tema de los signos de agrupación y podrás saber más sobre la jerarquía de operaciones.
Puedes construir tu propia ruleta, o hacer un sorteo de enunciados numéricos y jugar con las personas que vivan contigo. Usa los materiales que tengas disponibles.
Un capítulo del libro “El hombre que calculaba”, narra una divertida anécdota con un mercader que tenía una tienda llamada, los cuatro cuatros, para conocerla, observa el siguiente video: - El hombre que calculaba
El texto del video se recupera del libro: El hombre que calculaba, Autor: Malba Tahan. Nº de páginas:226. Editores Noriega.
Puedes formar al menos los números del 0 al 10, utilizando cuatro cuatros. Será un buen preámbulo, ya que en la siguiente lección profundizarás en esta actividad, haciendo uso de la jerarquía de operaciones; que cabe señalar es una convención muy importante, pues te ayudará a llegar a un resultado correcto común. Y así evitar conflictos.
El reto de hoy:
Si ya tienes tu libro de Matemáticas de primer grado, Te retamos a ubicar en él este tema, y resolver todo lo que puedas para practicar.
Si aún no cuentas con tu libro de texto, puedes encontrar los vínculos de los libros al final de la sección o en la página de la SEP. También puedes pedir ayuda, y retroalimentación a distancia de tus maestras o maestros, cuando sea posible.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/