Habilidades matemáticas I. Secuencias
Habilidades matemáticas I. Secuencias
Aprendizaje esperado: desarrolla habilidades que le permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Énfasis: desarrollar habilidades matemáticas. Secuencias.
¿Qué vamos a aprender?
Anota en tu cuaderno cualquier idea o inquietud que surja al resolver las situaciones que se estudian.
¿Qué hacemos?
¿Sabes qué es una secuencia?
Es una secuencia es una serie de números con un comportamiento determinado.
El término secuencia deriva del latín “sequentĭa”, que puede traducirse como “continuación”. Una secuencia, por lo tanto, es una serie de hechos o de elementos que mantienen una relación entre sí.
En Matemáticas, una secuencia o una sucesión es un grupo de números o de otros elementos matemáticos que forman un conjunto ordenado, es decir, que cada elemento guarda una especie de patrón entre sí.
Revisa diferentes tipos de secuencias y para cada reactivo, se dará la respuesta que se considere correcta y así se anota en la hoja de respuestas. De este modo, al final se pueden verificar las respuestas.

Tú puedes anotar en tu cuaderno el número de la pregunta y el inciso de la respuesta para que al final, sepas cuántas acertaste.
Se comienza con la primera secuencia numérica.

Porque a cada número de la secuencia se le suman 4 y se obtiene 19.
Una forma de encontrar el patrón de una secuencia es verificar la relación entre sus elementos, que en este caso es sumar 4.

La diferencia entre los elementos es 4, por tanto, el siguiente elemento es: 15 más 4 igual a 19.
La opción correcta es el inciso b).
La segunda secuencia numérica es:

El número es 36.
Pero ¿cuál es la estrategia utilizada para determinar el número 36?
Se utilizó una estrategia similar a la anterior, pero en este caso no se suman 4; al primer término se le suman 3, al segundo término se le suman 5, al tercer término se le suman 7, y así sucesivamente.
En el sexto término se le suman 11, es decir: 25 más 11 es igual a 36

Pero esta secuencia también se obtiene al elevar al cuadrado el número de cada término.
Por ejemplo: 1 al cuadrado igual a 1; 2 al cuadrado igual a 4; 3 al cuadrado igual a 9; 4 al cuadrado igual a 16 y 5 al cuadrado igual a 25.
De acuerdo con el patrón, el sexto término es igual a 6 al cuadrado, cuyo resultado es 36.

Ambas estrategias parecen viables porque se llega al mismo resultado.
En muchas ocasiones, la solución correcta a un problema se obtiene por diversos procedimientos.
Y para comprobarlo, se analiza la tercera secuencia numérica:

¿Cuál inciso es el correcto?
Es el inciso a).
En este caso, se tiene una combinación de un producto y una suma, y los elementos de la secuencia se determinan:
5 por 2 igual a 10,
10 más 1 igual a 11,
11 por 2 igual a 22,
Y 22 más 1 igual a 23.
Por lo tanto, el sexto elemento de la serie es: 23 por 2 igual a 46.

El inciso a) es el correcto.
Sin embargo, no todas las sucesiones son numéricas. Existen las sucesiones pictóricas, de las que se muestra un ejemplo.
Se dice que son secuencias espaciales porque son un conjunto de signos o imágenes ordenados de acuerdo con un principio.
Para saber más, se sigue con la cuarta secuencia espacial:
Observa las siguientes figuras:
¿Puedes reconocer qué sucede con éstas?
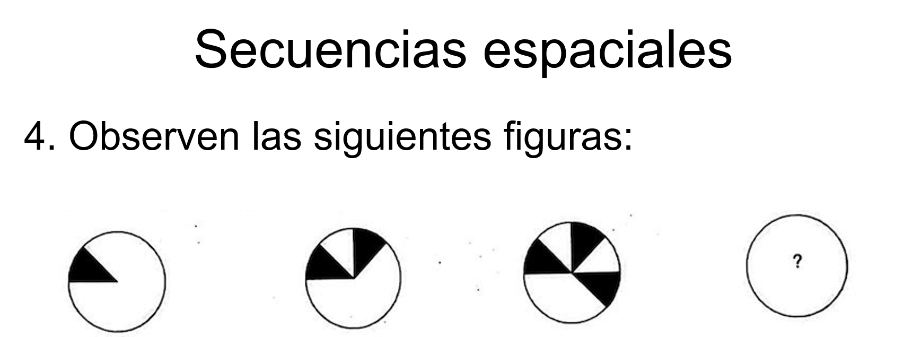
Se observa que a cada figura se le agrega un triángulo de color.
Entonces, si se puede saber cuál figura sigue, antes de mostrar los incisos.
La siguiente figura es un círculo con cuatro triángulos de color.
Antes de corroborar esta respuesta, se debe destacar que la habilidad matemática se desarrolla para acertar con precisión los reactivos.
Es decir, si al momento de leer el reactivo procesas la respuesta, posteriormente al observar los incisos, sólo debes verificar la que es correcta.
Por ejemplo: De las siguientes figuras, ¿con cuál continúa la secuencia?
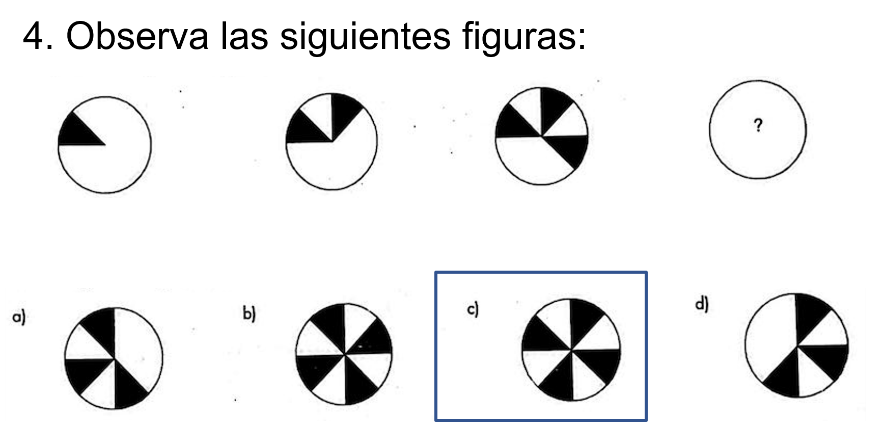
En la siguiente figura en la secuencia era un círculo con cuatro triángulos de color. Entonces, ¿por qué no puede ser el b)?
Por la posición que tiene cada triángulo.
Lo primero es identificar el patrón o regla de la secuencia.
Para este caso, se indica el número de elementos sombreados en cada circunferencia que aumenta de uno en uno. Por tanto, la cuarta circunferencia tiene cuatro elementos sombreados.
De este modo, las opciones correspondientes son los incisos b) y c). Sin embargo, al considerar la posición de los elementos sombreados, la respuesta correcta es el inciso c).
Es una buena estrategia el analizar cada reactivo y adelantarse a la posible respuesta.
Si la pones en práctica, puedes tener excelentes resultados.
De este modo, se sigue con la quinta secuencia:
Observa las siguientes figuras:
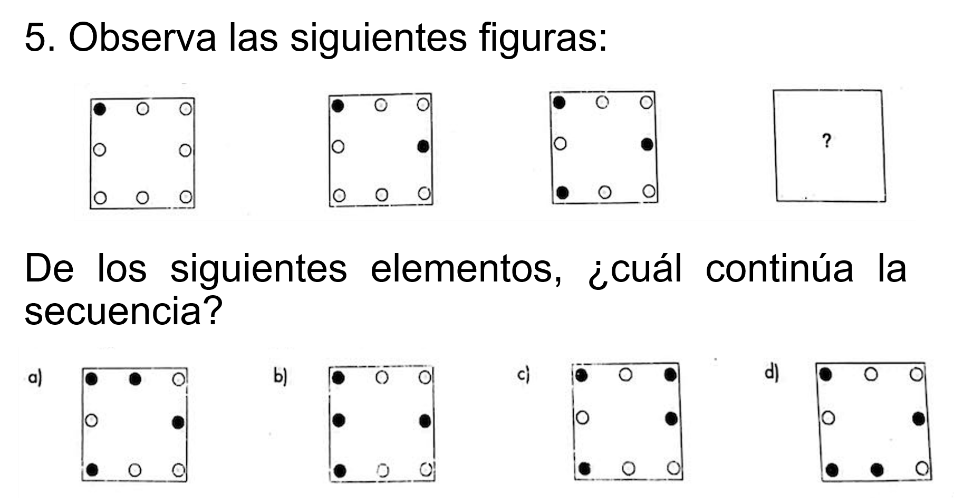
De los elementos en la imagen ¿con cuál continúa la secuencia?
Es el inciso b).
Verifica la respuesta.
En la secuencia, el número de elementos sombreados aumenta.
Además, existen dos círculos de separación, por lo tanto, la respuesta correcta es el inciso a).
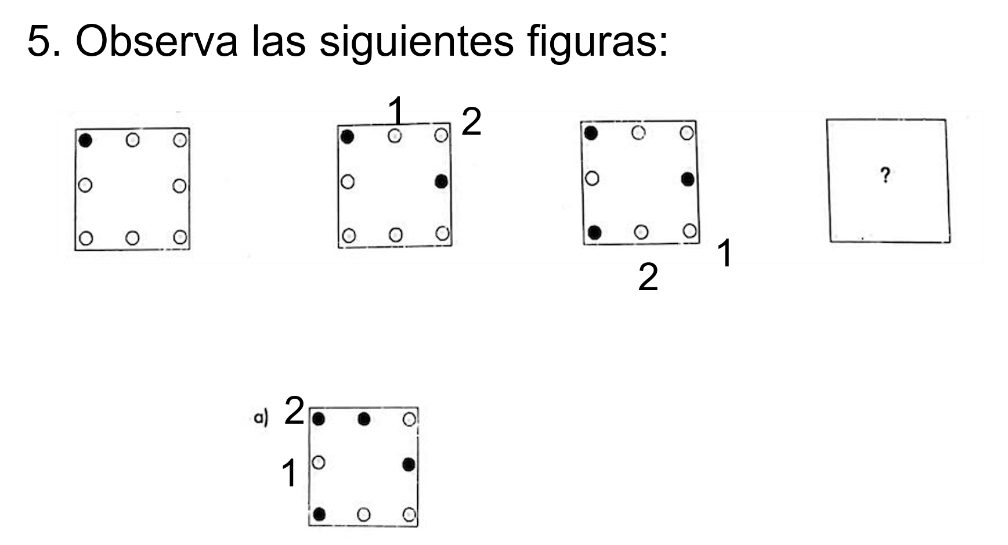
Es decir que, la respuesta fue incorrecta.
Por ello es indispensable comprobar cada inciso.
Con los conocimientos adquiridos, se siguen con secuencias de Geometría Espacial.
Es decir, que son como las anteriores, pero utilizando figuras.
Este tipo de ejercicios tienen como propósito determinar una figura en tercera dimensión si gira o se construye sobre la misma.
Se sigue entonces, con la sexta secuencia:
Se tiene en la imagen la siguiente figura:
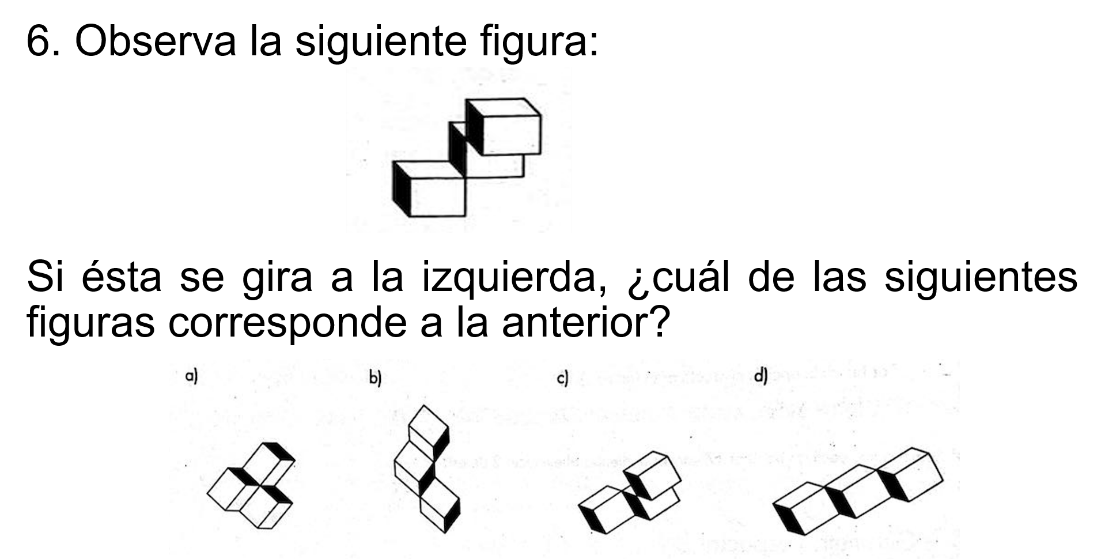
Si el giro es a la izquierda, la respuesta correcta es el inciso b).
De la figura inicial se analiza la posición que guarda, para después realizar el giro solicitado.
Por tanto, la opción correcta es el inciso b).
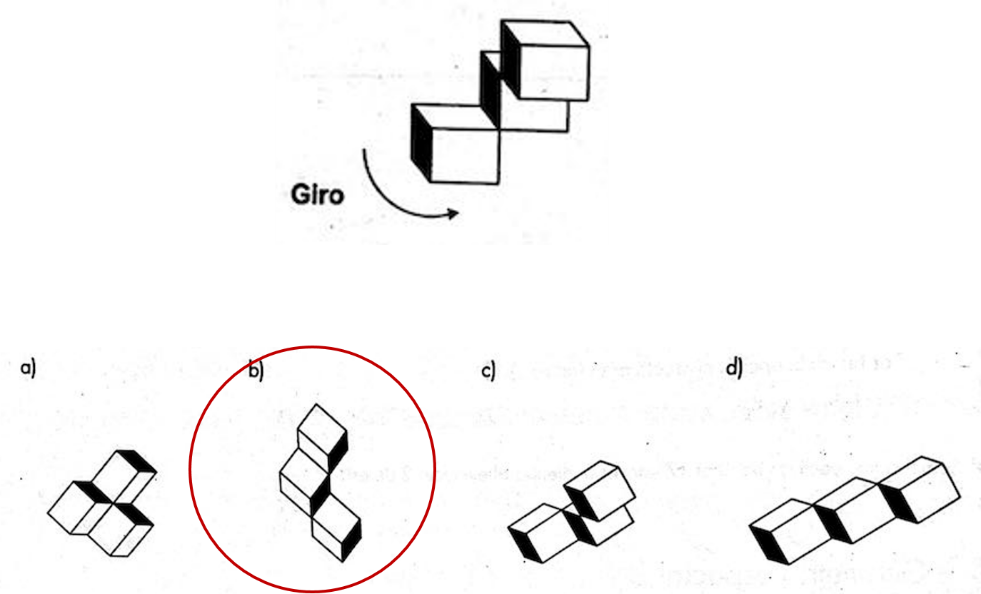
Es importante que, en este tipo de sucesiones, se observe detenidamente las características que poseen las figuras en su posición original.
Esto con el propósito de encontrar la pauta y así elegir la respuesta correcta.
Y a continuación, la séptima secuencia:
Determina el cubo correspondiente al desarrollo plano. ¿Cuál inciso se considera el correcto?
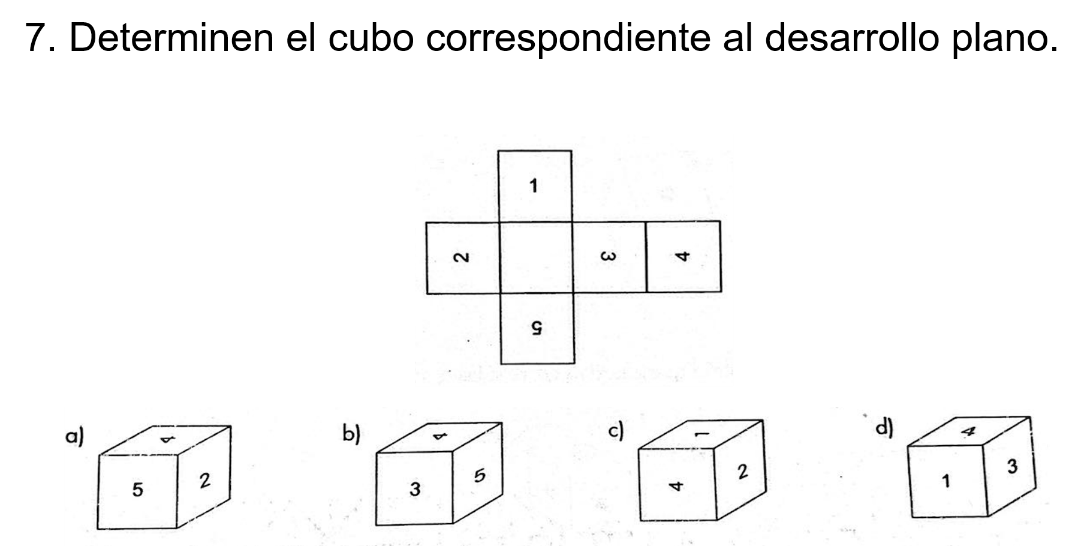
Esta vez requiere de un análisis más minucioso, el inciso c).
Verifica cada uno de los incisos para encontrar la respuesta correcta.
Comienza con el inciso d). ¿Qué se observa entre los números del desarrollo plano y este cubo?
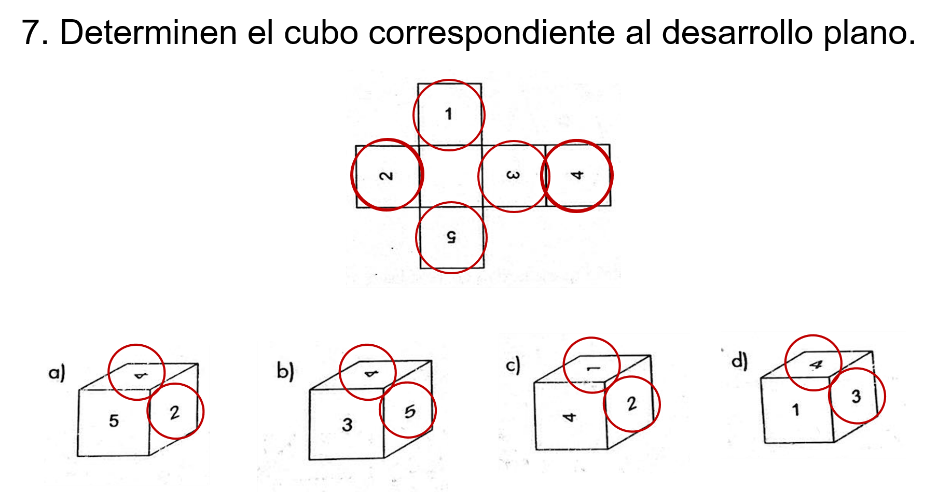
En el desarrollo plano, la parte superior del número cuatro coincide con la parte superior del tres.
Pero en el inciso d) no se encuentra de esa manera, porque el costado del número cuatro coincide con la parte superior del número tres.
Porque para el inciso c), el número uno con el número dos, de acuerdo con el desarrollo plano, estaría de lado. Sin embargo, en el cubo formado no es así; la parte inferior del número uno coincide con la parte superior del número dos.
Pero, ¿qué se observa entre los números del desarrollo plano del cubo en el inciso b)?
En el desarrollo plano, la parte lateral del número cuatro coincide con la parte superior del número cinco.
Y para el inciso b), no se encuentra de esa manera porque el costado del número cuatro coincide con la parte superior del número cinco.
Mientras que para el caso del inciso “a”, de acuerdo con el desarrollo plano, la parte superior del número cuatro coincide con la parte superior del número tres, y el pie del número cuatro coincide con la parte superior del número dos.
De este modo, se tiene que la respuesta correcta es el inciso a).
Si se te dificulta o no logras visualizar la posición de los números, se te recomienda construir el desarrollo plano y armar el cubo poniendo los números al igual que en el desarrollo plano. De este modo, cuando lo armes, sabrás la posición que toman, así es más sencillo observar cada movimiento.
Tras resolverlo, se sigue con la octava secuencia.
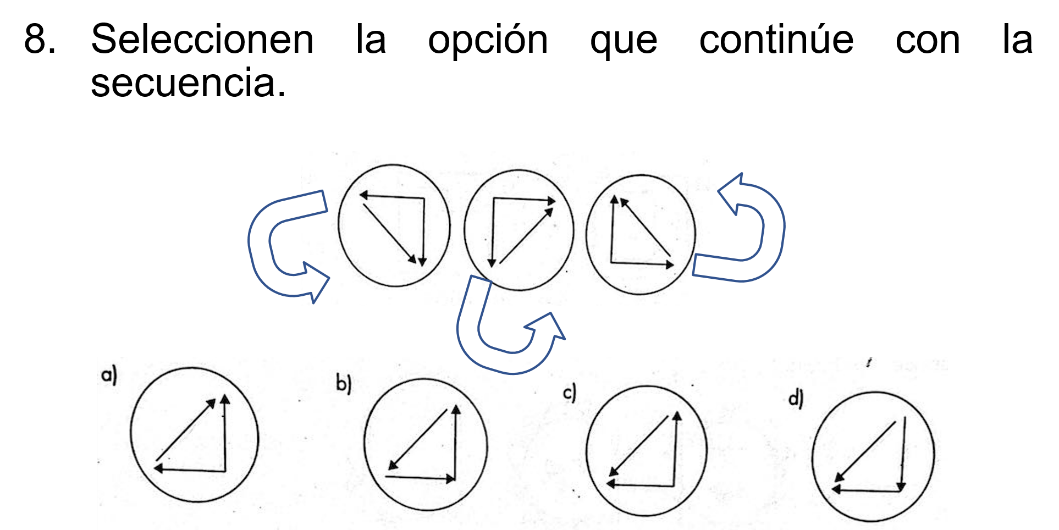
Antes de mostrar los incisos, analiza el comportamiento de las figuras.
Se puede observar que la figura va girando hacia la izquierda.
Entonces, ¿cuál inciso consideras es el correcto: “a”, “b”, “c” o “d”?
El inciso c).
Cabe destacar que las cuatro opciones están en la misma posición, pero quien determina la respuesta es la posición de las fechas.
Ya se sabe que estos ejercicios te permiten desarrollar habilidades matemáticas y son una herramienta para solucionar otro tipo de ejercicios.
¿En cuáles otras secuencias es aplicable este conocimiento?
Lo puedes observar en la novena secuencia:
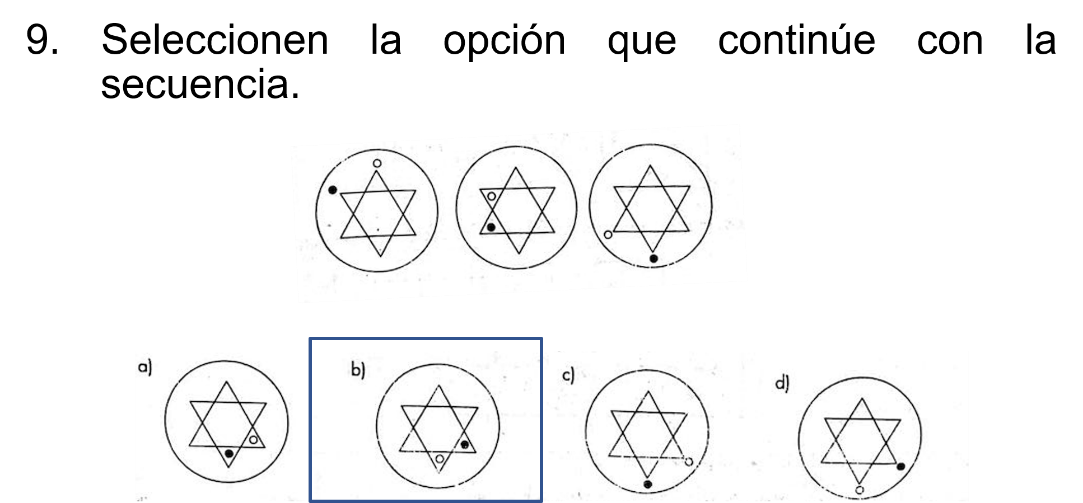
En la imagen se puede observar que la estrella dentro de la circunferencia tiene dos puntos: Uno sombreado y el otro no.
Los dos puntos están afuera, después adentro y luego otra vez afuera.
Entonces, ¿qué inciso consideras es el correcto?
Observa el orden en que se encuentran los puntos.
Basándose en lo anterior, la respuesta correcta es el inciso b).
En cada secuencia se necesita de un carácter observador para reconocer cada detalle.
En este tipo de reactivos, se debe fijar la atención en cada figura: Si gira o cambia de posición, y así contar con más elementos para llegar a la respuesta correcta.
Practica con un ejemplo más, la décima secuencia:
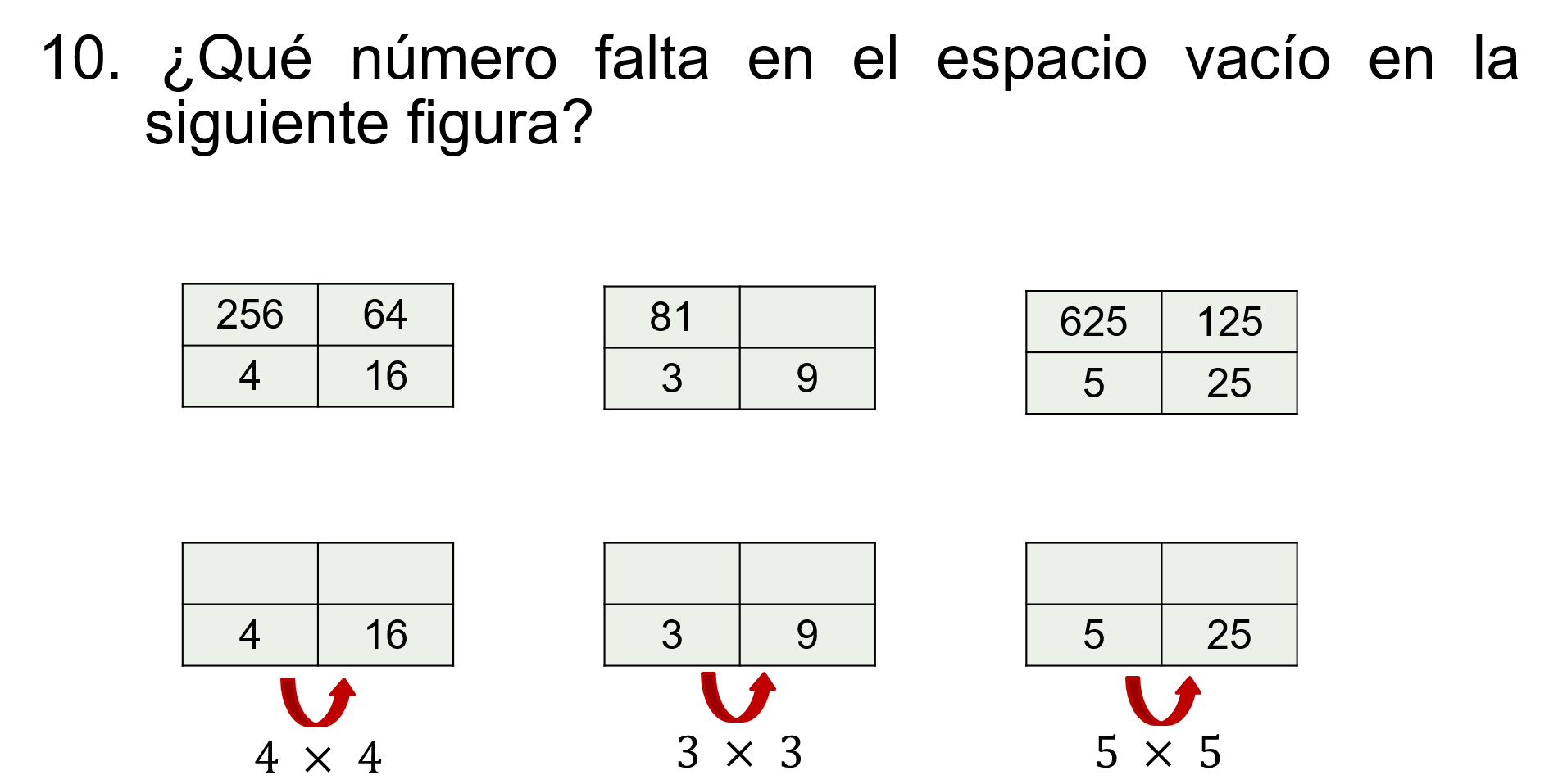
Analiza el comportamiento que existe entre los números de cada rectángulo, como ya se ha hecho en los ejemplos anteriores.
Recuerda que siempre hay una relación entre las secuencias.
Sigue la siguiente pista: Entre el 4 y el 16, ¿qué operación permite obtener el 16 a partir del número 4?
Si se multiplica 4 por 4 se obtiene 16.
Y con el 3, ¿qué operación se implica para obtener 9?
Si se multiplica 3 por 3, es 9.
Entonces en el siguiente rectángulo, se multiplica 5 por 5 para obtener 25.
De este modo, se puede observar la relación que hay entre el 16 para obtener 64, y en la tercera tabla, la relación del 25 para obtener 125.
Uno de los rectángulos guarda un comportamiento para determinar el patrón.
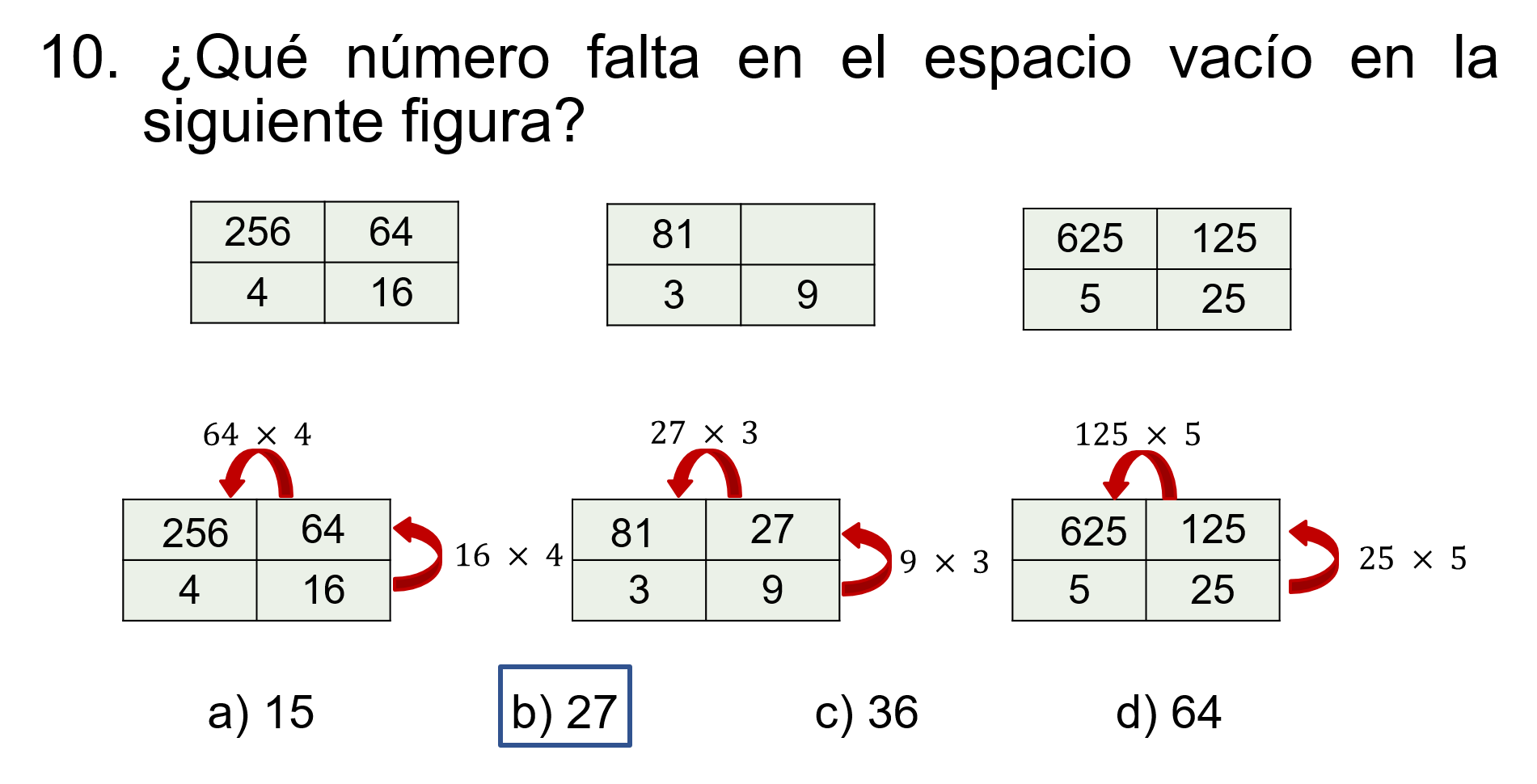
En la primera tabla, se multiplica 16 por 4, igual a 64, y en la última tabla 25 por 5 igual a 125.
Entonces en la tabla central, ¿cuál es la relación?
La respuesta es 27, porque 9 por 3 es 27.
De igual manera, 64 por 4 es 256; 27 por 3 es 81 y de 125 por 5 se obtiene 625.
En los incisos está: a)15, b) 27, c) 36, d) 64.
Y la respuesta correcta es el inciso b).
Se tiene dos secuencias adicionales como ejercicios.
Implica el mismo modo, tablas.
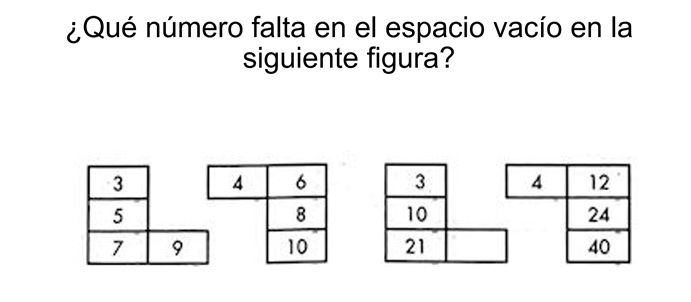
Analiza las figuras:
3 con 4; 5 con 6;
3 con 4 y 10 con 12.
La respuesta es 36.
Observa cómo existe una relación entre la primera tabla con la segunda, y otra relación entre la tercera y la cuarta tabla.
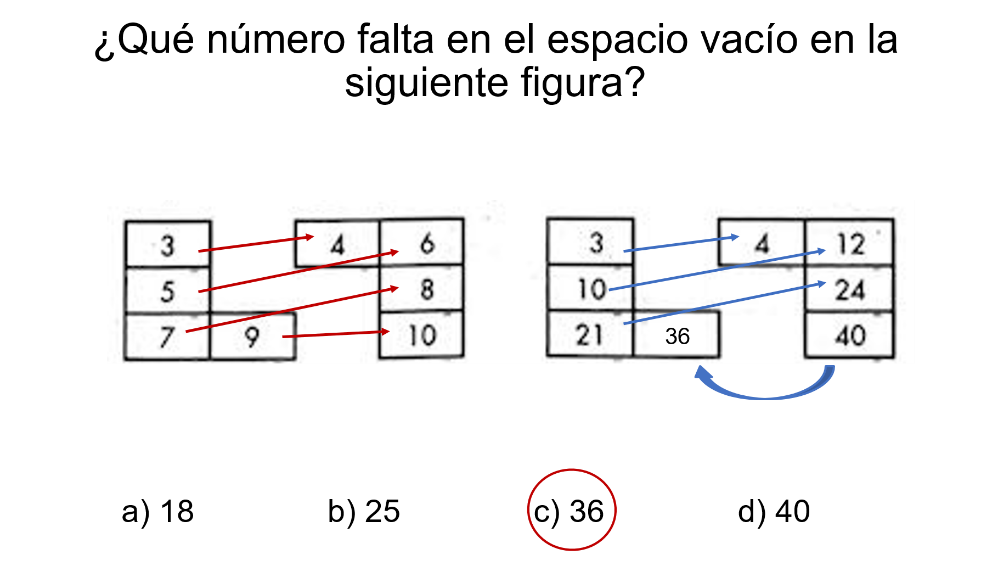
Si se analizan las dos primeras tablas:
Se puede comprobar que cada cuadrito que la compone, los números aumentan en uno.
Es decir, en la primera tabla está el número 3 y en la segunda tabla el primer número es 3 más 1, igual a 4.
Mientras que el segundo número es 5 y en la segunda tabla es 6, y así sucesivamente.
Al comparar las siguientes dos tablas, observa que del 3 al 4 aumenta uno; del 10 al 12 aumenta dos, y del 21 al 24 aumenta 3. En consecuencia, en la siguiente aumenta 4.
Por tanto, si en la cuarta tabla está el valor de 40, en la tercera tabla en el espacio vacío debe de ir 40 menos 4 igual a 36.
La respuesta es el inciso c)
Y por último la siguiente secuencia.
Implica una secuencia numérica.

La secuencia es 5.5 negativo, 3 negativo, 0.5 negativo, 2, posteriormente dos números faltantes, 9.5 y 12.
Es importante que en este tipo de secuencias numéricas observes detenidamente.
Ésta comienza con números negativos y llega a números positivos.
La secuencia es creciente, por lo tanto, se le está sumando una cifra.
Observa de 5.5 negativo a 3 negativo, la diferencia es de 2.5.
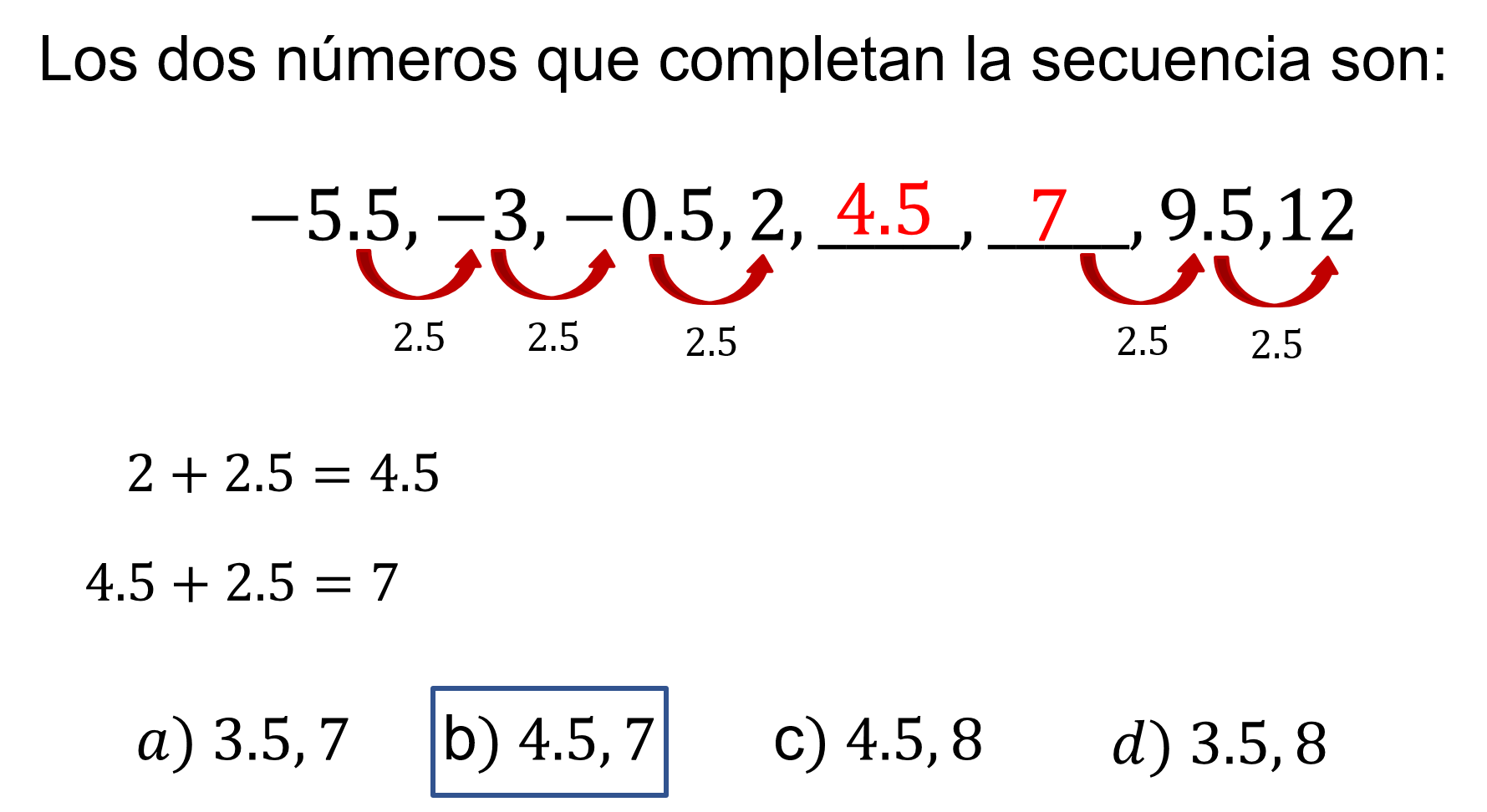
De 3 negativo a 0.5 negativo la diferencia es 2.5.
De 0.5 negativo a 2 la diferencia vuelve a ser 2.5.
Por lo tanto, el patrón es sumar 2.5 a cada término, entonces, si a 2 le sumas 2.5 se obtiene 4.5 y,
A 4.5 se le suma 2.5 se obtiene 7.
4.5 y 7 son los dos números faltantes en la secuencia.
Y si a 7 se le suma 2.5 se obtiene el siguiente término 9.5.
Y si, a 9.5 se le suma 2.5 se obtiene 12, el cual es el siguiente el término de la secuencia.
Por tanto, la respuesta correcta para esta secuencia es el inciso b).
Ahora revisa cuáles fueron las respuestas correctas.
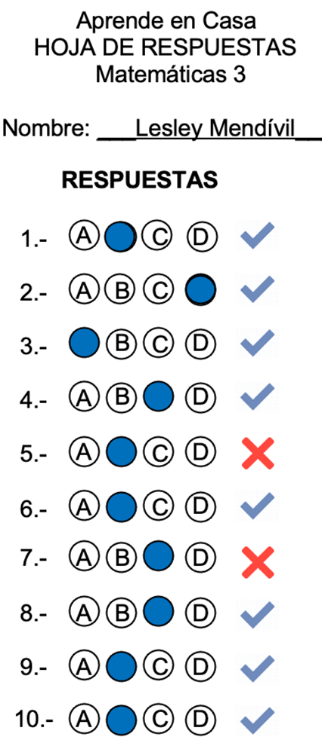
De los 10 reactivos, se obtuvieron 8 aciertos, lo cual significa que el porcentaje de efectividad fue del 80 por ciento.
Antes de concluir, se retoma lo aprendido durante la sesión al trabajar con el aprendizaje esperado: “Desarrolla habilidades que les permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias”.
Además, se trabajaron diversos reactivos tanto de secuencias numéricas como espaciales y de geometría espacial.
Y finalmente, se revisaron los aciertos de cada uno de los reactivos.
Se te recomienda tener presente lo trabajado y aplicarlo en diferentes secuencias.
Asimismo, ya sabes que al momento de anotar en hojas de respuesta como la que utilizó en la sesión, se deben registrar bien los alveolos para que el lector óptico que califica los lea correctamente.
El reto de hoy:
Reflexiona sobre las diversas estrategias que puedes utilizar para resolver de manera correcta reactivos de sucesiones.
Tu libro de texto de Matemáticas de tercer grado tiene ejercicios similares para realizar otras secuencias.
Es importante que practiques lo aprendido para lograr desarrollar habilidades matemáticas.
El matemático Stan Gudder dijo: “La esencia de las Matemáticas no es hacer las cosas simples complicadas, sino hacer las cosas complicadas simples”.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.