Gráficas de expresiones cuadráticas
Gráficas de expresiones cuadráticas
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: analizar las diferentes representaciones de una relación cuadrática. Partir de la expresión algebraica.
¿Qué vamos a aprender?
Ten a la mano tus materiales de trabajo. Utilizarás tu cuaderno, regla, lápiz o bolígrafo y lápices de colores
Registra en tus cuadernos las dudas, inquietudes o dificultades que surjan al resolver los planteamientos en esta lección.
Las expresiones cuadráticas o de segundo grado son aquellas que tienen un exponente máximo de dos en alguno de sus términos.
Entre otras opciones, las expresiones algebraicas de segundo grado se obtienen de la multiplicación de dos términos con exponente 1.
¿Qué hacemos?
Por ejemplo, al multiplicar x por x obtienes como resultado x al cuadrado.
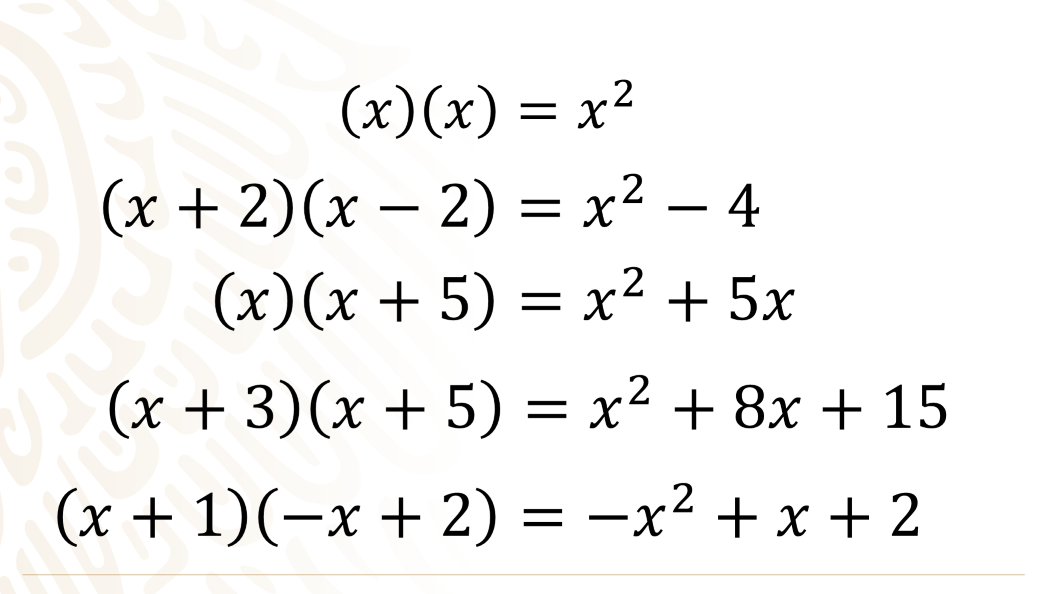
Si multiplicas los binomios conjugados x más 2 por x menos 2, resulta x cuadrada menos 4.
Al multiplicar x por x más 5, obtienes x al cuadrado más 5 x.
También puedes multiplicar x más 3 por x más 5, y el resultado es x cuadrada más 8x más 15.
Y, como último ejemplo, x más 1 que multiplica a x negativa más 2, de donde se obtiene x cuadrada negativa más x más 2.
Cada una de las expresiones anteriores es una expresión cuadrática porque el exponente máximo es 2.
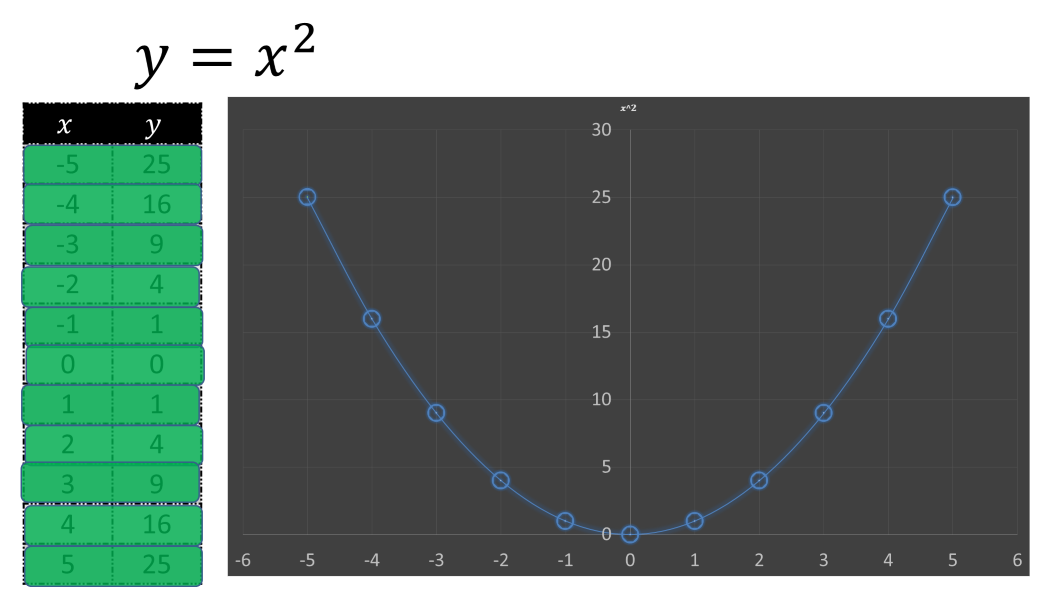
Toma el ejemplo más sencillo, x cuadrada, cuya gráfica es una curva llamada parábola.
A diferencia de las gráficas de relaciones lineales, no basta con obtener dos puntos para generar toda la gráfica, ya que no es una línea recta.
Antes de aprender a graficar esta expresión, debes hacer su correspondiente tabulación para obtener los datos que se graficarán.
Para poder tabular una expresión algebraica, debes decidir qué valores son de mayor utilidad para que la gráfica aporte la información necesaria para su análisis.
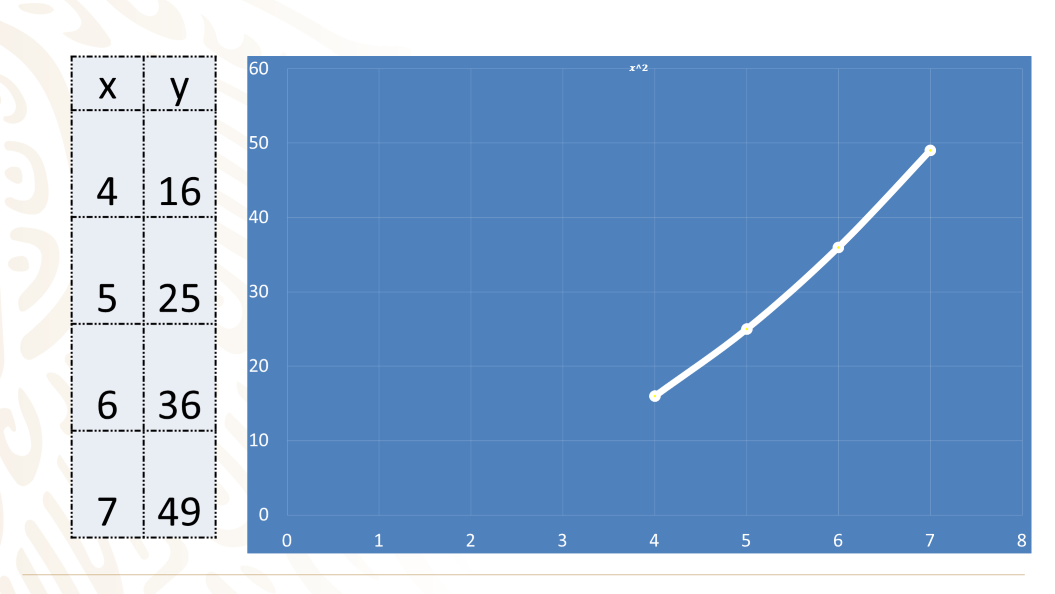
Por ejemplo, si decides tabular los valores 4, 5, 6 y 7 para la expresión x cuadrada, la gráfica que obtienes es la siguiente, y no aporta los datos necesarios para entender el comportamiento de este conjunto de datos.
Para la expresión x cuadrada, es conveniente ocupar los valores desde 5 negativo hasta 5 positivo para comenzar a darte una idea de cómo es que se comporta gráficamente. En casa, son libres de escoger un rango mayor de números para construir su propia tabulación, por ejemplo, desde 10 negativo hasta 10 positivo.
Para cada uno de los puntos de la tabulación, debes encontrar el valor de “y”, así, para el primer valor propuesto, 5 negativo, el valor que toma es 5 negativo al cuadrado, que da como resultado 25.
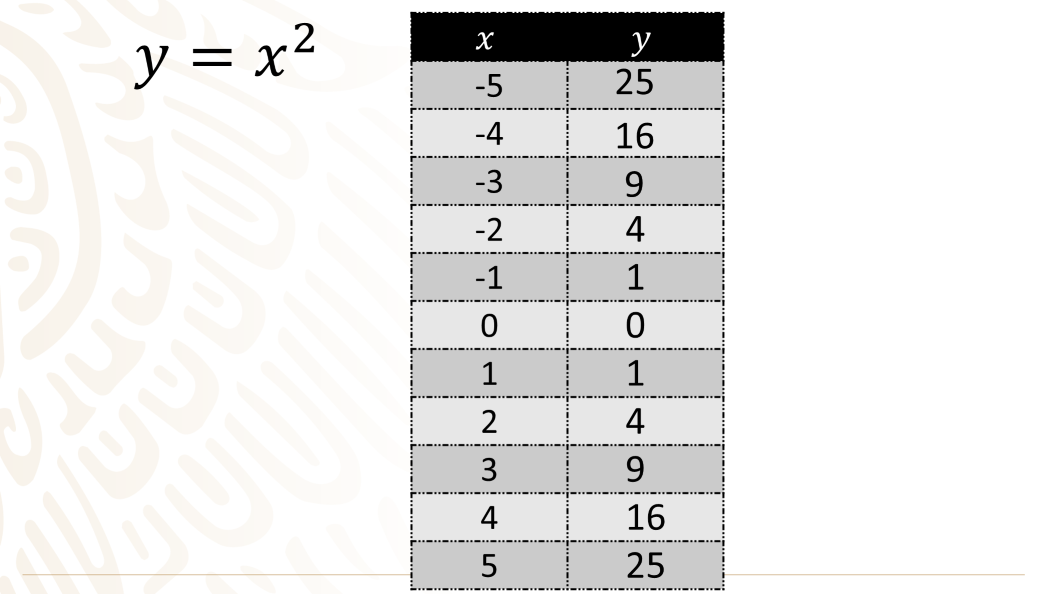
Para 4 negativo, el valor que toma es 16 positivo, porque 4 negativo al cuadrado es igual a 4 negativo por 4 negativo, que es igual 16.
Para 3 negativo, el valor de “y” es igual a 9 positivo. De esta forma, sigues calculando los valores correspondientes a cada valor de x hasta completar los propuestos en la tabulación.
Al sustituir 2 negativo en x de la función, obtienes que “ye” es igual a 4 positivo.
Al sustituir 1 negativo en la función, se obtiene “ye” igual a 1.
Sustituyes cero, se obtiene cero para “ye”.
En 1, otra vez se obtiene 1.
En 2, “y” es 4.
En 3, “y” es 9.
En 4, “y” es 16
Finalmente, sustituyes el valor de “x” en la función y = x al cuadrado, obtienes un valor de 25 para “y”.
De esta forma, obtienes valores suficientes para graficar la expresión x cuadrada.
Comienza por trazar los ejes coordenados x y “ye” con la escala correspondiente a los datos obtenidos en la tabulación.
Identifica 5 negativo y 5 positivo en el eje de las x, también llamado de las abscisas.
Considera desde 6 negativo hasta 6 positivo para que la gráfica no salga de la hoja.
Para los valores de “y”, el valor máximo que obtuviste es de 25, y el valor mínimo es de cero, por lo que trazarás el eje de las “y”, también conocido como eje de las ordenadas, desde 1 negativo hasta 30 positivo, dando también un margen extra.
Una vez que tienes delimitado el espacio con los ejes coordenados, encontrarás las parejas de puntos que se generaron en la tabulación.
Así, la primera pareja de coordenadas que obtuviste será 5 negativo en las abscisas y 25 positivo en las ordenadas.
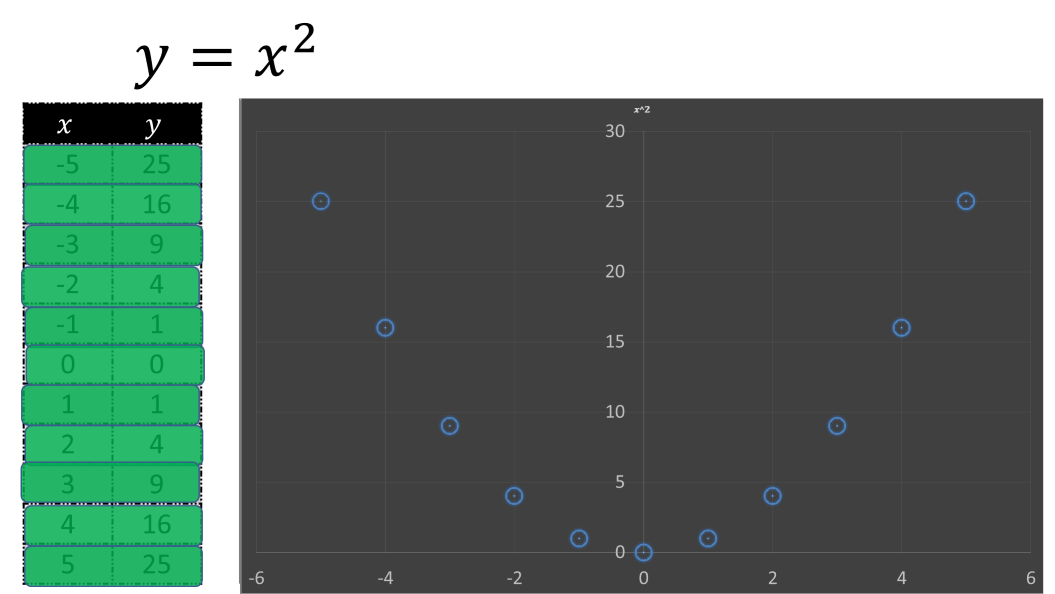
Las siguientes parejas de números son:
4 negativo coma 16 positivo
3 negativo coma 9 positivo
2 negativo coma 4 positivo
1 negativo coma 1 positivo
La coordenada en el origen cero coma cero
1 coma 1
2 coma 4
3 coma 9
4 coma 16
Y 5 coma 25
De esta manera, ya tienes el cálculo de los valores en la tabulación y las parejas de coordenadas que te servirán para trazar la gráfica de la expresión algebraica x al cuadrado.
Ya que tienes todos los puntos coordenados identificados, los unes para formar una primera representación gráfica de la expresión algebraica x al cuadrado, la cual es una parábola.
Para el siguiente ejercicio, realiza el mismo análisis comenzando con la expresión algebraica que, en este caso, es x cuadrada menos 4.
Y, para la tabulación, ocupas los mismos valores en el eje de las abscisas desde 5 negativo hasta 5 positivo, para después evaluar la expresión en cada uno de esos valores.
Añadirás una columna más en la tabulación, donde harás la sustitución de los valores de x en la función para obtener el valor de “y”, la variable dependiente.
y = x2 – 4
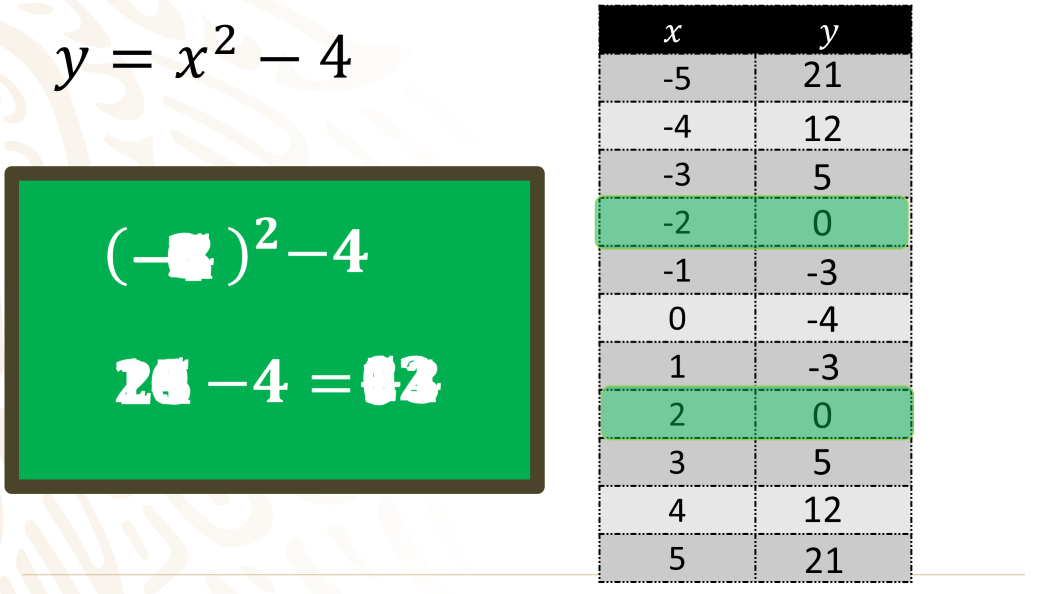
Así, para 5 negativo, en la sustitución escribes 5 negativo al cuadrado, menos 4, que, realizando las operaciones, da como resultado 25 menos 4, igual a 21.
Para 4 negativo, en la sustitución escribes 4 negativo al cuadrado menos 4, realizas las operaciones; 4 negativo al cuadrado es 16 menos 4, es igual a 12.
Para 3 negativo, sustituyes 3 negativo al cuadrado menos 4, que es igual a 9 menos 4; obtienes, al final, 5.
Para 2 negativo, sustituyes 2 negativo al cuadrado y le restas 4. El resultado de esta operación es igual a cero.
Sigues con el 1 negativo, donde después de operar obtienes 3 negativo.
En x igual a cero, el valor de “y” es 4 negativo.
En x igual a 1 obtienes 3 negativo.
En x igual a 2 obtienes nuevamente cero.
Para el valor de x igual a 3, obtienes una “y” igual a 5.
En 4 obtienes 12.
Y en 5 obtienes 21.
Ya tienes la tabulación de los datos que has propuesto para x. Ahora delimita los valores mostrados en el eje de las abscisas y ordenadas para trazar la gráfica correctamente según la expresión cuadrática.
En las abscisas ocupas valores entre 5 negativo y 5 positivo. Y en las ordenadas el valor máximo que obtienes es de 21, y el mínimo es de 4 negativo, por lo que puedes trazar los ejes desde 6 negativo hasta 6 positivo en las abscisas, y de 5 negativo a 25 positivo en las ordenadas.
Separa de la tabulación los pares ordenados para poder graficar los puntos.
Los pares ordenados quedan de la siguiente manera:
La primera pareja de coordenadas que obtienes fue 5 negativo en las abscisas y 21 positivo en las ordenadas.
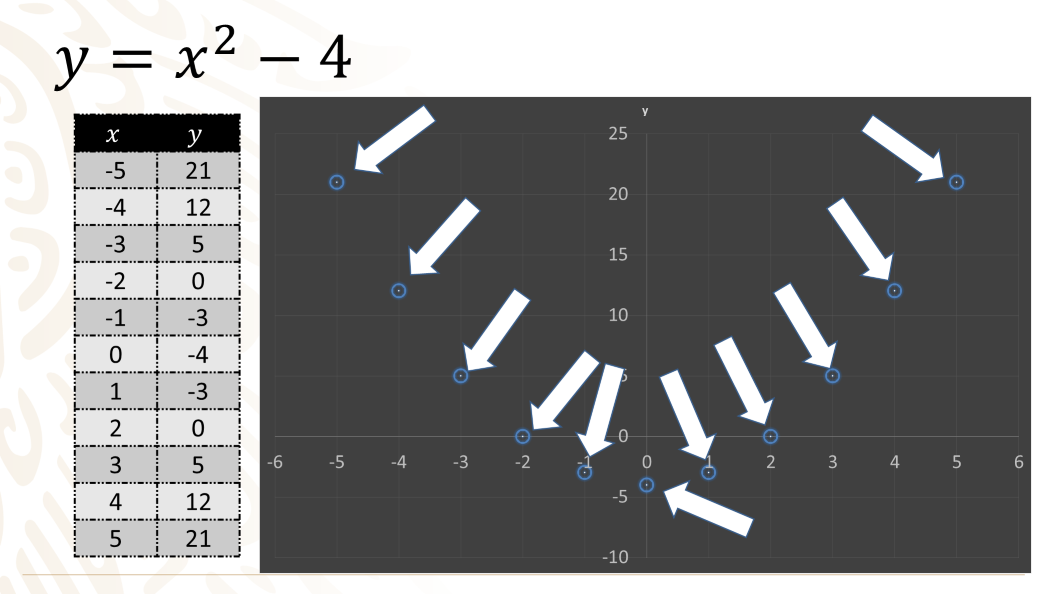
Las siguientes parejas de números son:
4 negativo coma 12 positivo
3 negativo coma 5 positivo
2 negativo coma 0 positivo
1 negativo coma 3 negativo
La coordenada cero coma 4 negativo
1 coma 3 negativo
2 coma 0
3 coma 5
4 coma 12
Y 5 coma 21
Si identificas cada una de las parejas de coordenadas en el plano cartesiano, es posible trazar la gráfica que representa a la expresión cuadrática: x cuadrada menos 4.
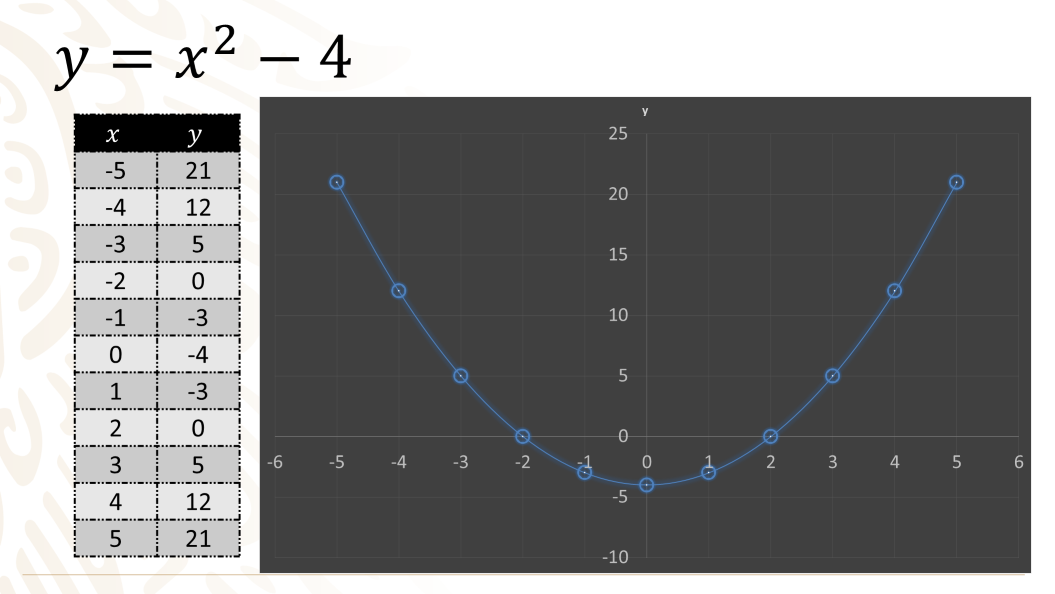
En ella puedes visualizar que los valores negativos de “y” son menos que los positivos
Para el siguiente ejercicio, trabajarás con la función:
x^2 + 8x + 15
Necesitarás ocupar valores más grandes y puedes valernos de una hoja de cálculo electrónica para poder construir la tabulación y la gráfica que represente esta expresión.
Ya sabes que una hoja de cálculo es una herramienta que, como una calculadora, ayuda a simplificar trabajo en procesos repetitivos y bien definidos.
Con esta herramienta también puedes desglosar resultados parciales de la ecuación para analizar cómo se comporta, sólo hay que tener cuidado con la jerarquía de operaciones.
Sabes que las potencias tienen mayor jerarquía; después, la multiplicación y división, y por último, las sumas y las restas. Sabes también que esta jerarquía puede alterarse con el uso de paréntesis.
Una celda, en la hoja de cálculo, puede tomar tres tipos diferentes de valor: puede ser texto, número o una operación.
Además, cada celda se identifica con sus coordenadas en la hoja donde estás trabajando; primero obtienes la columna, marcada con una letra del abecedario, y después se obtiene la fila con un número consecutivo que comienza en 1. Así, la primera celda se llama A1.
En la celda A1 puedes escribir una etiqueta de texto que indique que los valores de esa columna corresponden a “x”, igual que en tu cuaderno. Para esta tabulación usarás los valores desde 10 negativo hasta 10 positivo.
En la hoja de cálculo se pueden autocompletar esos valores de forma automática; únicamente se registran los 2 primeros valores. En la celda A2 escribes el número 10 negativo, y en la celda A3 escribes el número 9 negativo. Después los seleccionas y arrastras desde la esquina inferior derecha hasta llegar al valor de 10. Todas estas celdas son del tipo número y puedes hacer operaciones con ellas.
En la celda B1 escribes una nueva etiqueta de texto, en esta única ocasión vas a desglosar cada término de la expresión que quieres graficar para entender el proceso y poder visualizar los resultados en la hoja de cálculo.
El primer término de la expresión es x al cuadrado. Y una vez que lo has identificado, utilizarás la operación de multiplicación para obtener sus valores.
La forma de indicar que una celda es del tipo operación es comenzar escribiendo el signo de igual, lo que harás en la celda B2. Después le indicas el primer valor de la operación, en este caso elegirás que sea el valor que tiene x en esa fila, es decir, A2. Esta referencia se logra escribiendo la celda o usando las flechas del cursor hasta resaltarla.
Usa el símbolo de asterisco para indicar la multiplicación y, como el primer término de la expresión es x al cuadrado, necesitas el mismo valor nuevamente, la celda A2.
Así, la celda B2 va a obtener el valor de x cuadrada.
Para autocompletar el resultado correspondiente a cada uno de los valores de x asignados en la columna A, arrastras desde la esquina inferior derecha de la celda y con ello llenas automáticamente todos los valores establecidos para x al cuadrado.
El segundo término de la expresión algebraica es 8x y pondrás la etiqueta de texto en la celda C1. Para la celda C2, indicarás la operación de multiplicación, comienzas con el signo de igual, seguido de 8 por el valor de x, que está en A2.
Así, el primer resultado es 80 negativo. Copias la operación en el resto de la columna y ya tienes todos los valores propuestos de x multiplicados por 8.
En el tercer término no necesita una operación, pues es el valor constante 15. Por única ocasión vas a replicar el valor en la columna D para que sea visible en todos valores propuestos de x.
En la celda D1 usas la etiqueta de texto ‘15’ porque es un título. En la celda D2 escribes el valor 15 porque es un número, y lo copias en el resto de las celdas.
Ya tienes los valores de la expresión x2+8x+15 separados en las columnas B, C y D. Ahora sólo falta sumarlas y obtendrás el valor total de la expresión.

La suma la indicarás en la columna E, y en la celda E1 escribes la etiqueta de texto “y”; en la celda E2, la operación de suma de las tres celdas anteriores. Primero, el signo de igual para indicar la operación; después, el primer valor que, en este caso, es B2, que corresponde a x al cuadrado; el signo de más; a continuación, la celda C2 que en el ejercicio corresponde a 8x, nuevamente el signo de más y, por último, la celda D2, que tiene el valor de 15.
Los resultados de la columna E son los correspondientes al eje de las ordenadas. Y ahora sí, puedes graficar.
Al igual que en el cuaderno, puedes escribir cada una de las coordenadas x coma y. Sólo le pides a la hoja de cálculo que copie los valores en una columna diferente.
La selección de los datos a graficar debe corresponder con tus necesidades. En este caso, la columna x y la columna “y” se seleccionan para indicarle a la hoja de cálculo cuáles son los datos a graficar.

Selecciona la opción de insertar gráfica de dispersión, procura que sea la opción que une los puntos con una línea, y verifica que las coordenadas coincidan con los datos, si no es así, quiere decir que te equivocaste en la selección del tipo de gráfica.
Tienes la posibilidad de ajustar los datos a graficar y obtener la curva que estás acostumbrado a visualizar. Observa que la hoja de cálculo va a permitir seleccionar con qué datos quieres trabajar.
En todos los casos que trabajas has obtenido en la gráfica una línea curva llamada parábola.
Realiza un último problema con la expresión algebraica:
–x2 + x + 2
Para su tabulación, escoge valores desde 4 negativo hasta 5 positivo.
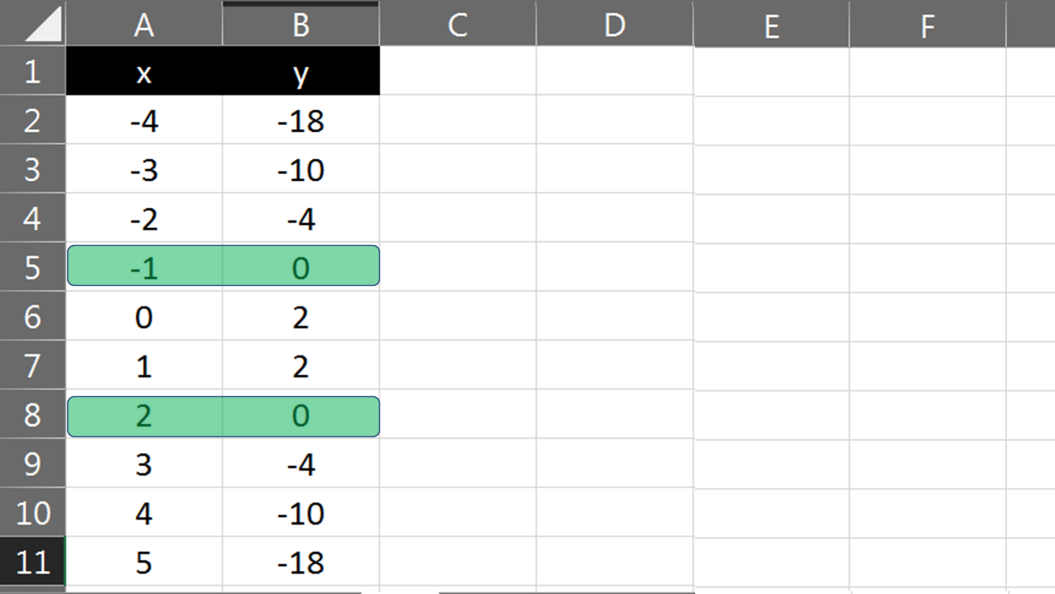
En esta ocasión calcula las operaciones de cada valor propuesto para “x” en una sola celda. Para lograrlo, necesitas escribir la siguiente operación:
= negativo, paréntesis x^2, cerramos paréntesis.
Con esto indicas que quieres obtener el negativo de la x al cuadrado, no el cuadrado de x negativo. Y en la hoja de cálculo, el símbolo que ocupas para una potencia es éste, y lo obtienes tecleando a la vez Alt+94.
Después sumas el valor de x, que es la celda A2, y finalmente sumas el número constante 2.
Si copias la operación para todos los valores de x que has propuesto, obtienes los valores: 18 negativo, 10 negativo, 4 negativo, cero y nuevamente, te acostumbraste a marcarlo, 2, otra vez, 2, y nuevamente cero, que resaltas con algún color, 4 negativo, 10 negativo y 18 negativo.
Ya con los datos de la tabulación, puedes graficar eligiendo una gráfica de dispersión, y de esta manera, la gráfica se traza automáticamente.
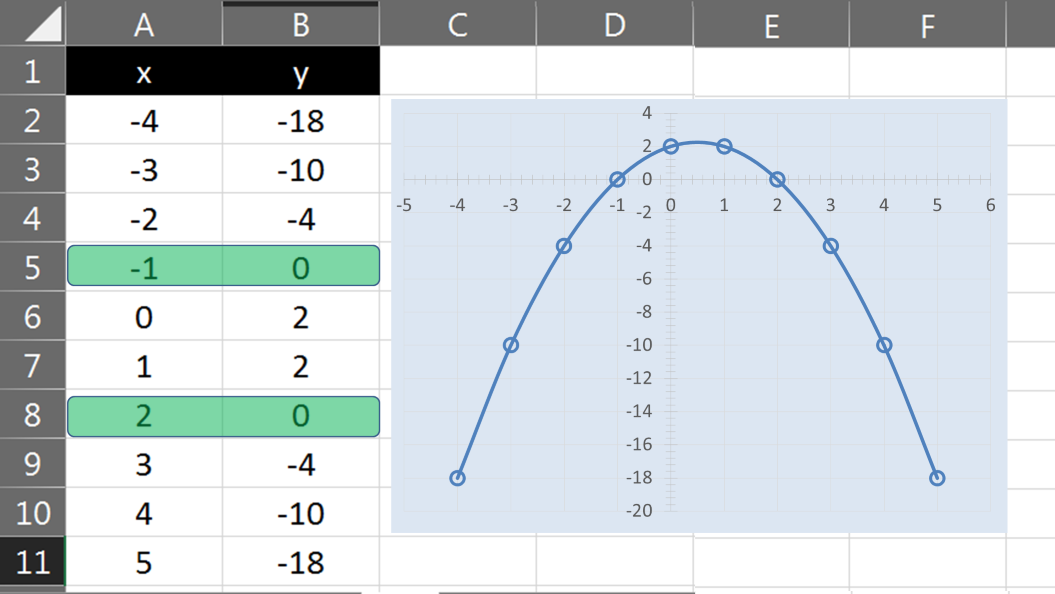
Puedes observar que el primer signo negativo hizo que la gráfica quedara invertida con respecto a los primeros tres ejercicios.
Con estos ejercicios has logrado representar, en una gráfica, una expresión cuadrática.
Primero generas un registro tabular de cada una de las parejas de puntos, con éstos elaboras una gráfica.
Utiliza esta nueva herramienta en una situación financiera, que indica qué decisión tomar de acuerdo con el análisis de una gráfica. Observa el siguiente ejemplo:
Un amigo que es médico veterinario decidió comenzar su propio negocio. Entre todo lo que tuvo que hacer contrató un estudio de publicidad. La empresa de publicidad le envió la siguiente carta.
“Estimado doctor, con base en toda la información que nos ha proporcionado, nuestro departamento de especialistas ha calculado la curva que representará los resultados de su inversión con nosotros.
Representada por la curva 0.5x cuadrada menos 4x más 6 de la siguiente gráfica y para una inversión máxima de $10 000.”
Con base en la carta, puedes preguntarte:

Los valores en los que vas a tabular serán desde cero, lo que indicaría que no se invirtió en publicidad, y 10, representando los $10 000 del máximo de inversión recomendado.
Ahora evalúa la expresión recomendada por la empresa de publicidad en esos valores con intervalos de 1.
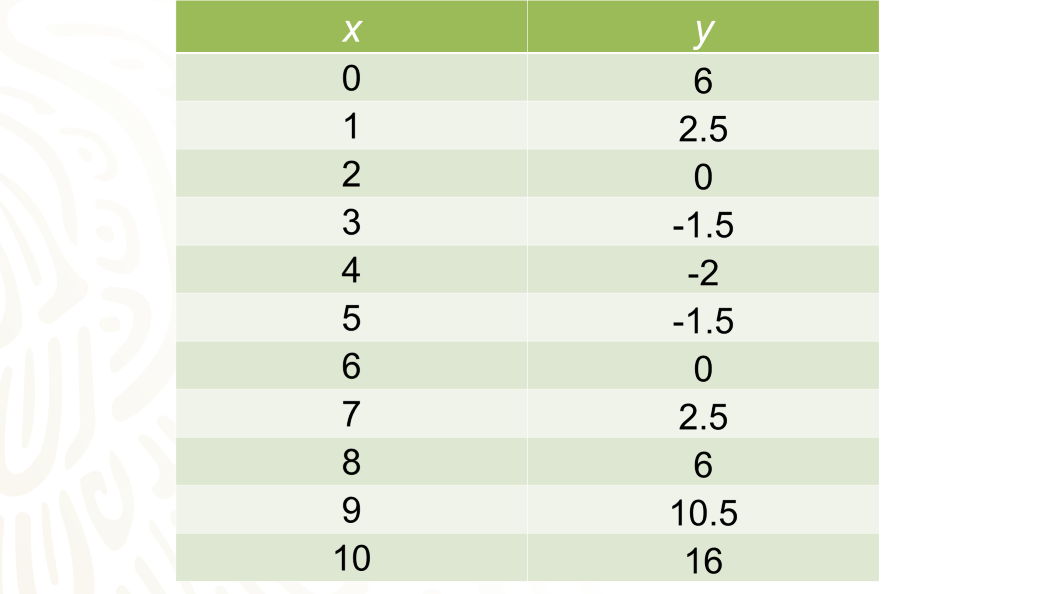
Los resultados los utilizas para generar los datos y después la gráfica. En el eje de las abscisas representas la inversión en miles de pesos, y en el eje de las ordenadas representas el beneficio que obtendrá el amigo en su empresa.
Las parejas ordenadas son:
En cero, el beneficio es de 6.
Si la inversión es de 1, el beneficio es de 2.5.
En una inversión de 2, el beneficio es ¡cero!
En 3, 4, 5 y 6, el beneficio es 1.5 negativo, 2 negativo, 1.5 negativo y cero, respectivamente.
En 7, 8, 9 y 10 el beneficio es 2.5, 6, 10.5 y 16, respectivamente.
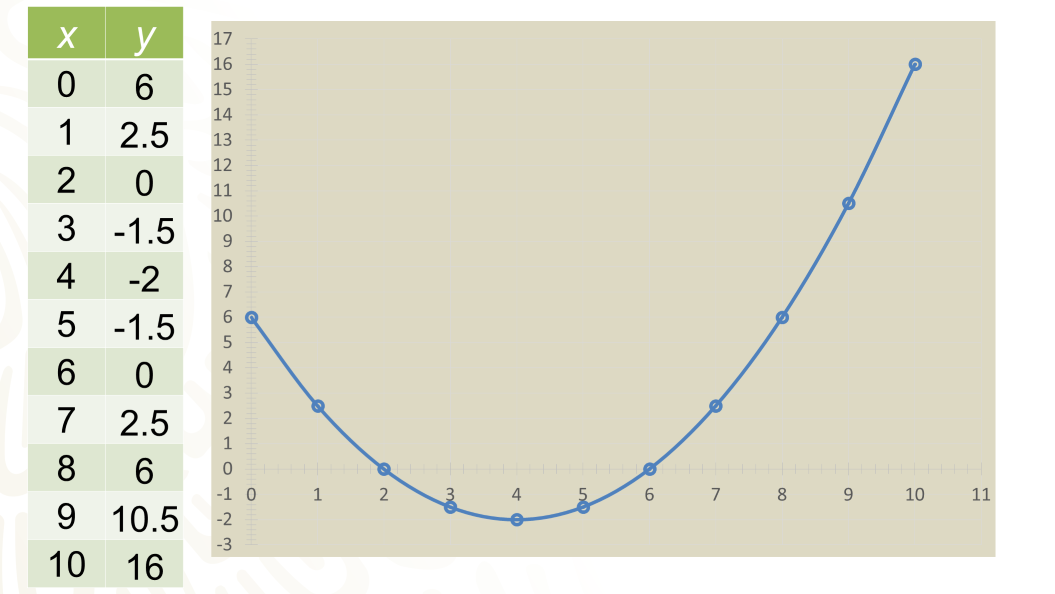
Ya con la gráfica trazada, puedes hacer el análisis de cuánto pudo invertir en publicidad.
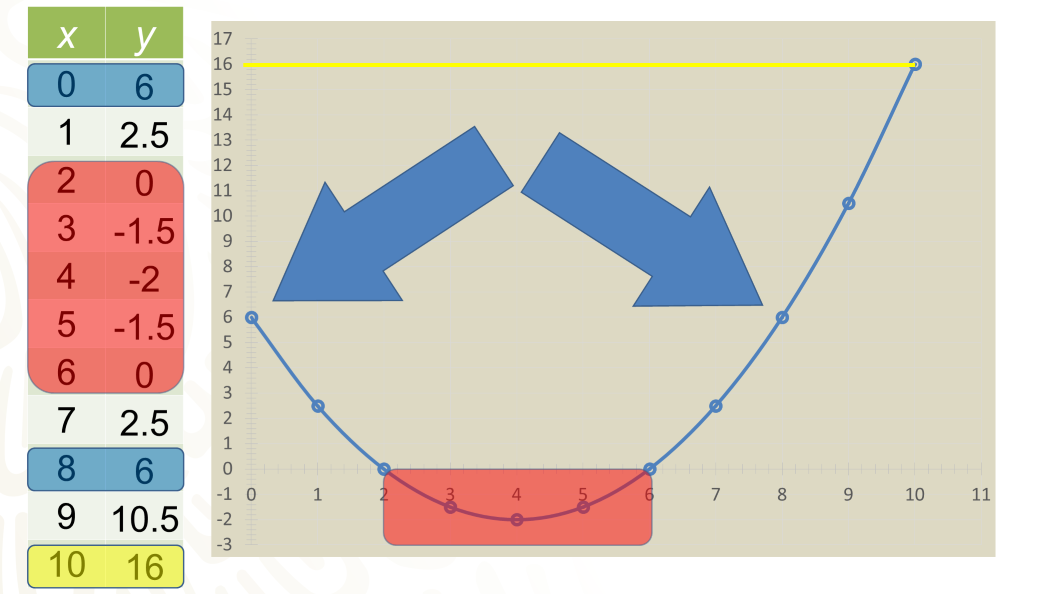
La primera pregunta es: ¿para qué valores de la inversión la empresa tiene pérdidas?
En la gráfica, los valores de las ordenadas negativas representan las pérdidas; por lo que la respuesta es: cuando se invierten entre $2 000 y $6 000.
Para el tope de $10 000 invertidos en publicidad, ¿cuál será el beneficio que se obtiene?
La gráfica indica que el beneficio será de $16 000.
¿Cuál es el beneficio si no se invierte en publicidad?
Si no hace inversión alguna, mantendría una ganancia de $6 000, como siempre.
¿Hay algún otro valor de la inversión para el cual se obtiene el mismo beneficio?
Si invertía $8 000, obtenía los mismos $6 000 que si no hubiera invertido nada de dinero en publicidad.
Por lo tanto, la decisión más sensata para invertir en publicidad con esa empresa, son cantidades mayores a $8 000 hasta el tope de los $10 000.
Él decidió invertir los $10 000 y sus ganancias alcanzaron lo estimado por los especialistas.
Con esta situación has terminado con el estudio de la gráfica de expresiones cuadráticas.
Siempre ten presente que se debe tener orden y exactitud al hacer la tabulación, y hacer gráficas limpias, con regla y con valores correctos para su adecuada interpretación.
El reto de hoy:
Revisa tus libros de texto para afirmar, rectificar o consultar sus posibles dudas, así como resolver los ejercicios propuestos en el tema de obtener una gráfica de una expresión cuadrática.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: