Gauss: medir el cosmos y evaluar errores
Gauss: medir el cosmos y evaluar errores
Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.
Énfasis: reconocer las aportaciones de Gauss a las matemáticas.
¿Qué vamos a aprender?
Conocerás a uno de los matemáticos más importantes e influyentes de la historia.
Realizó grandes aportes en casi todas las ramas de las matemáticas.
Es la vida y obra de Carl Friedrich Gauss para concebir las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.
Ten a la mano tu cuaderno, regla y lápiz o bolígrafo.
¿Qué hacemos?
En el año 2006, más de 3 000 físicos astrónomos de todo el mundo se reunieron en la ciudad de Praga, en la República Checa, para decidir si Plutón seguiría siendo considerado un planeta o no.
La votación se llevó a cabo el 26 de agosto de ese año y la decisión fue contundente: Plutón dejaría de ser un planeta como lo son, por ejemplo, la Tierra o Saturno, pero ¿cómo se consideraría entonces a Plutón?, ¿qué tipo de objeto sería en el sistema solar?
La solución fue crear una nueva categoría de objetos que no cumplieran con las características para ser considerados planetas y, además, no fueran lunas.
Así, había cuatro cuerpos con una situación similar a la de Plutón, y la nueva categoría de objetos parecidos a Plutón se llamaría “planetas enanos”.
Los planetas enanos son cinco: Plutón, Makemake, Haumea, Eris y Ceres.
Ceres era considerado hasta entonces como el mayor de los asteroides del cinturón de asteroides entre las órbitas del planeta Marte y del gigantesco y gaseoso Júpiter.
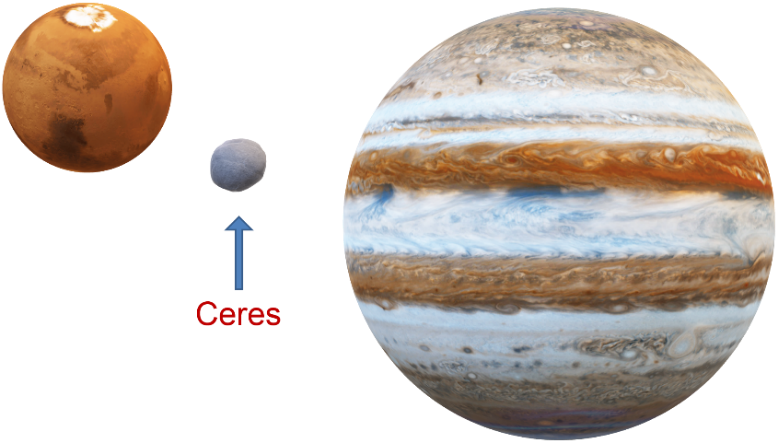
El asteroide Ceres, de casi mil kilómetros de diámetro, fue descubierto el 1 de enero de 1801 por un sacerdote y astrónomo italiano llamado Giuseppe Piazzi.

Él lo observó y registró durante 40 noches hasta que desapareció debido al brillo solar, es decir, el asteroide Ceres se ocultó en su órbita alrededor del Sol.

Piazzi esperaba que Ceres reapareciera en el firmamento después de algunos días, pero no consiguió verlo de nuevo.
Algunos astrónomos intentaron descifrar el misterio de la nueva posición de Ceres, pero en esa época no se disponía de herramientas matemáticas para calcular con exactitud la trayectoria del asteroide.
La decepción por no ver a Ceres fue muy grande y tuvieron que esperar largos meses, hasta que un joven matemático de tan sólo 24 años les indicó el lugar preciso donde debían apuntar sus telescopios para encontrar de nuevo a Ceres.
Así, el 9 de diciembre de 1801, los astrónomos quedaron impresionados al comprobar, a través de sus instrumentos astronómicos, que el asteroide Ceres se encontraba exactamente en la posición indicada por el joven matemático Carl Friedrich Gauss.
Nació el 30 de abril de 1777 en la ciudad de Brunswick, en Alemania.
Fue hijo único. Su padre se llamó Geghard Gauss, y su madre, Dorothea Benze.
Vivía en una casa, pequeña y humilde, la calle en la que nació se llamaba Berdengraben, aunque después vivió en la calle Vilgenestrasse, cerca del canal de la ciudad.
En una ocasión, cuando tenía tres o cuatro años, se cayó al canal y fue rescatado por un campesino que pasaba por ahí.
Gauss aprendió primero a contar antes de leer.
Una de sus anécdotas favoritas es que, siendo un pequeño niño, ayudó a su padre a corregirle una suma realizada por él.
Así le evitó a su padre pagar de más a los empleados a su cargo.
En 1784 ingresó a la escuela elemental, el profesor Büttner le dedicó mayor atención en comparación a sus compañeros.
Incluso le obsequió varios libros de matemáticas, los cuales él mismo pagó de su propio bolsillo.
Cuando tenía 9 años, en la clase del profesor Büttner, les pidió sumar los primeros cien números naturales, considerándolo una laboriosa tarea que les llevaría un cierto tiempo.
Sin embargo, mientras el resto de la clase se encontraba apenas iniciando las primeras sumas, Gauss se levantó, fue al escritorio del profesor y le entregó la pizarra.
El profesor tomó la pizarra, observó el resultado: 5 050, y, sorprendido, le preguntó qué cómo era posible que obtuviera el resultado correcto tan pronto.
Desde luego que no sumó número a número desde el 1 hasta el 100 como el resto de sus compañeros. Se dio cuenta de que la primera cifra (1) y la última (100) sumadas daban 101, la misma cantidad de sumar la segunda cifra (2) y la penúltima (99).
Además, al sumar la tercera (3) y la antepenúltima (98) igualmente sumaban 101 y así para el resto de las parejas.
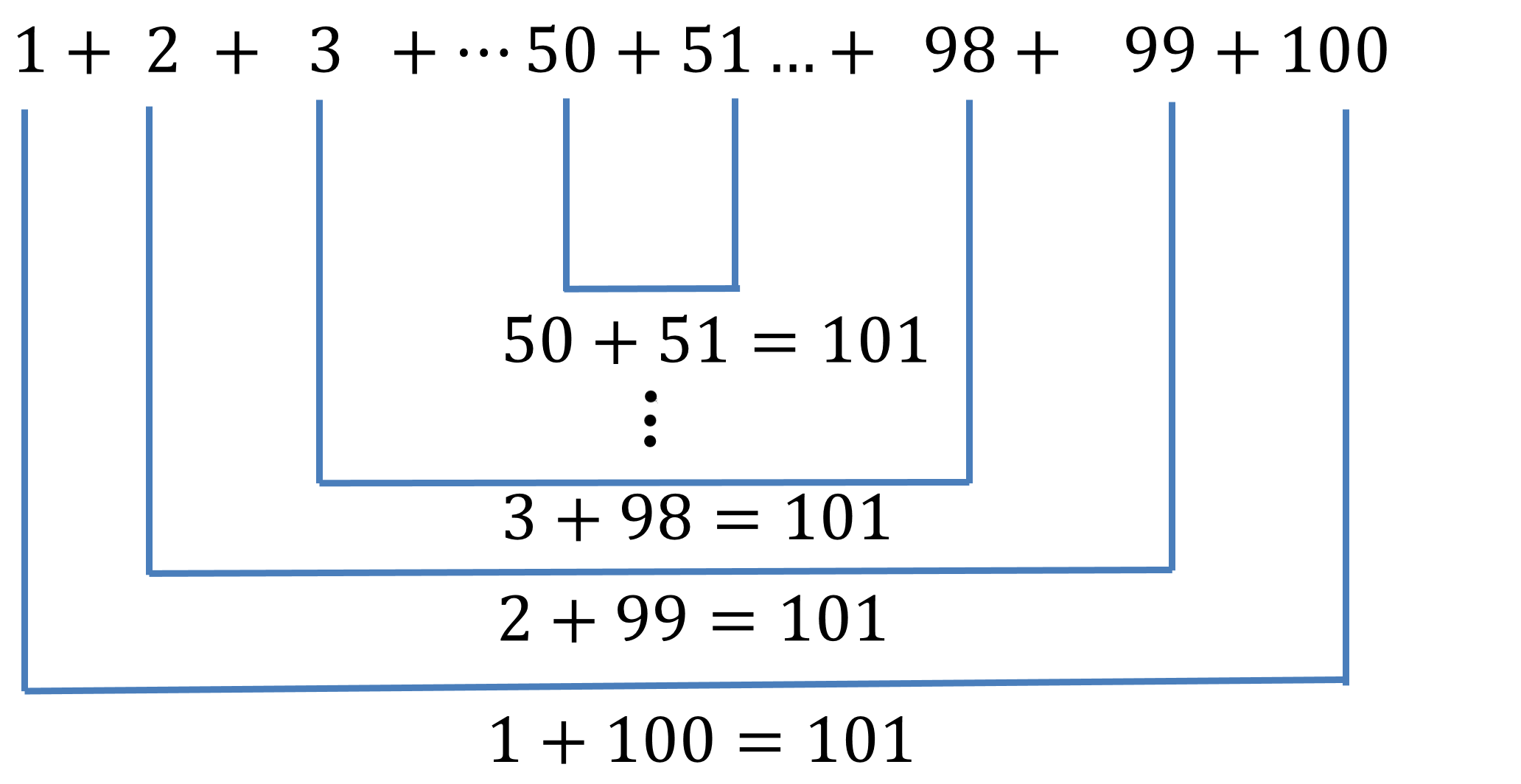
El razonamiento lo prosiguió sin problema: 1 más 100, igual a 2 más 99, igual a 3 más 98, igual a todas las parejas hasta la última central: 50 más 5 igual a 101.
Había 50 parejas de números que sumaban 101 y cuyo producto es 5 050.
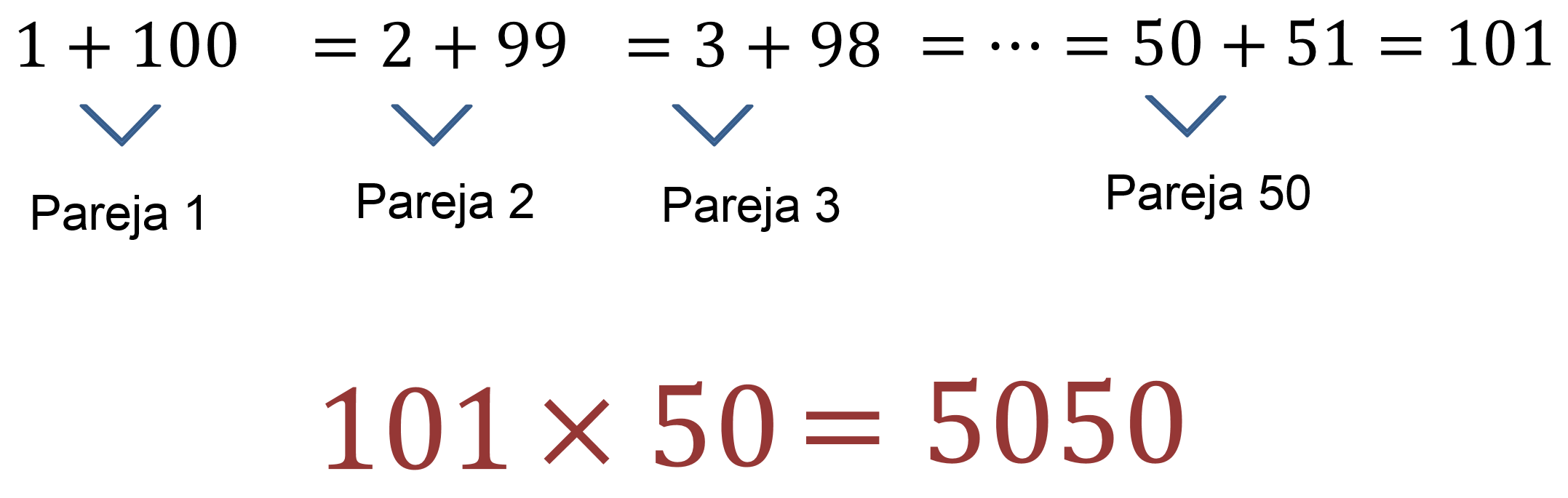
Aplicó, intuitivamente, la fórmula de la suma de los términos de una sucesión aritmética a la edad de tan sólo 9 años.
Una sucesión aritmética es una serie de números tales que la diferencia de dos términos sucesivos cualesquiera de la secuencia es una constante; por ejemplo, en el problema puesto por el profesor de Gauss sobre la suma de los primeros 100 números naturales, la diferencia entre ellos es 1.
Y para que puedas resolver fácilmente cualquier problema relacionado con la suma de los primeros “n” números naturales, observa la siguiente expresión sencilla.
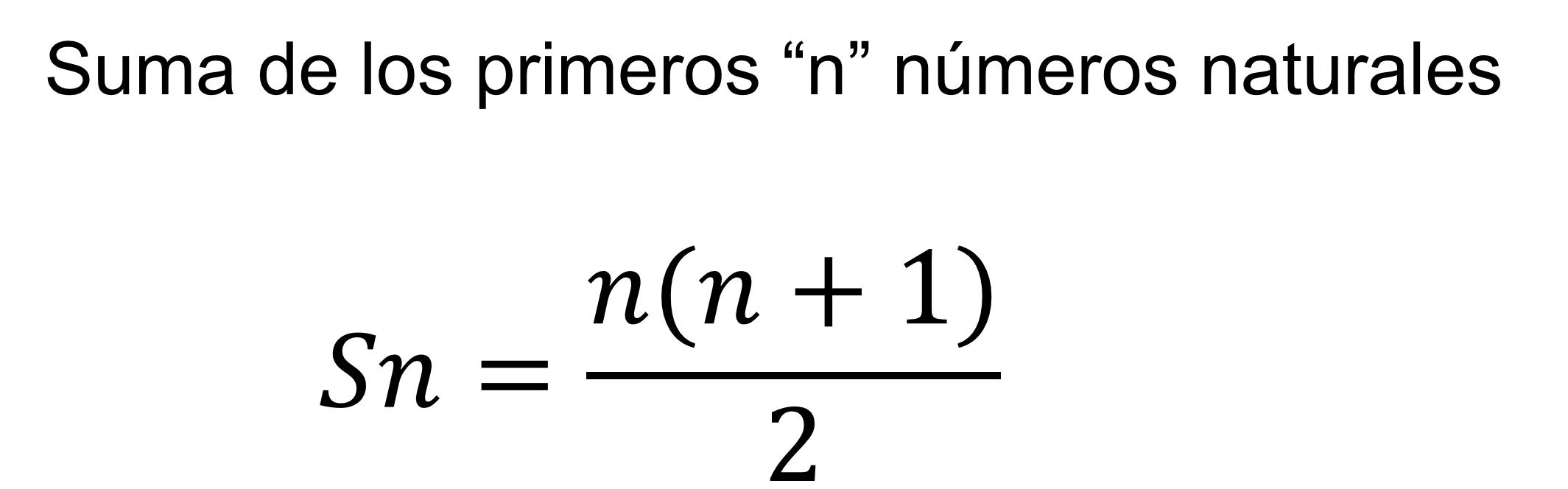
Así, si sustituyes en la ecuación:
“n” es igual a 100.
Sustituyendo en la fórmula, la suma de los primeros 100 números naturales se obtiene 5 050.
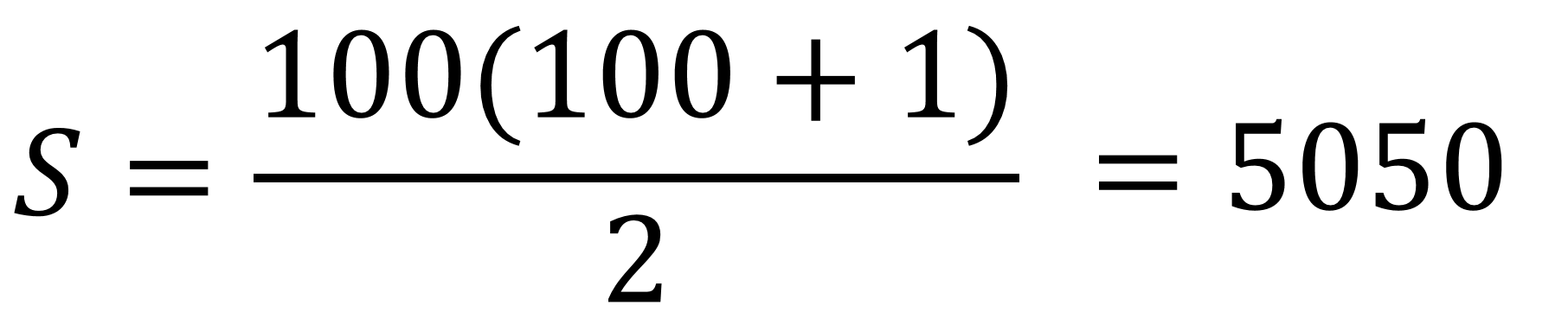
Resuelve el siguiente ejercicio.
Encuentra la suma de todos los números naturales desde el 1 al 200.
Regresando a la vida de Gauss, a los 10 años, descubrió dos métodos para calcular raíces cuadradas de números de 50 cifras decimales.
Ingresó a la secundaria en el año de 1788, tenía entonces 11 años cumplidos, ahí tuvo la oportunidad de leer los Principia de Newton, y el Ars Conjectandi de Bernoulli.
En 1791, con 14 años, fue presentado ante el duque Carlos Guillermo Ferdinand, quien quedó impresionado por sus logros y descubrimientos matemáticos, y lo apoyó para continuar sus estudios.
Un año después ingresó al Collegium Carolinum y en 1795 dejó su pequeña ciudad para continuar sus estudios en la Universidad de Gotinga.
También tenía interés por las lenguas clásicas, y casi se dedica al latín y al griego.
Sin embargo, las matemáticas nunca lo dejaron y fue entonces por esa época cuando logró una de sus más grandes aportaciones en el ámbito de la geometría, se refiere al problema geométrico de la construcción de polígonos con regla y compás.
La construcción de los polígonos regulares de 3, 4, 5 y 15 lados, así como la de los polígonos obtenidos de los anteriores multiplicando el número de lados por una potencia de dos era ya conocida por los antiguos griegos, como Euclides.
Hasta el momento, no se había encontrado aún un método para construir ningún otro polígono regular, como el heptadecágono.
Es decir, un polígono con diecisiete lados, diecisiete ángulos y diecisiete vértices, ni siquiera se sabía si tal método existía.
Este era un problema que los matemáticos habían intentado solucionar durante más de 2 000 años y no lo habían logrado.

Entonces, en 1796, después de aproximadamente seis meses de trabajo intenso y gran pasión, Gauss demostró que sí se puede construir un heptadecágono con regla y compás en el sentido clásico de este tipo de construcciones.
Observa la construcción del heptadecágono.
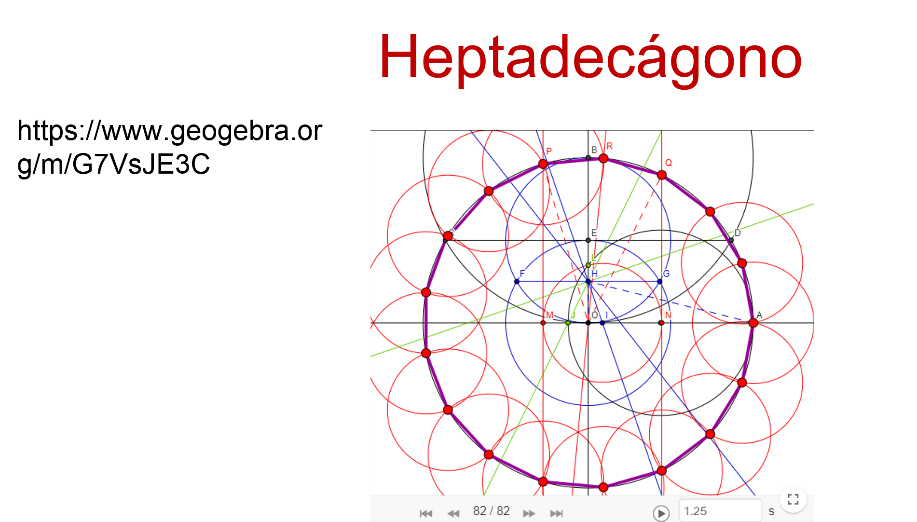
https://www.geogebra.org/m/G7VsJE3C
Lo obtuvo cuando apenas contaba con 19 años e incluso descubrió una ecuación para encontrar todos los polígonos regulares a construirse usando solamente regla y compás, en total, 31 polígonos.
Y la condición para su construcción con regla y compás de un polígono regular con un número de lados impar, sólo es posible cuando el número de lados es un número primo de la serie 3, 5, 17, 257 y 65 537 o un producto de dos o más de estos números.
Por cierto, en esa época comenzó a llevar un diario matemático donde anotaba algunas de sus ideas y descubrimientos.
Era como su bitácora donde plasmaba cada uno de sus avances de manera breve para no perder de vista ninguno.
Las primeras anotaciones son del año 1796, justo a los 19 años y, la última anotación tiene fecha del 9 de julio de 1914.
En total fueron 19 páginas donde registró 146 resultados.
Unas de las notas decían:

Y para continuar con sus grandes aportaciones a las matemáticas, en su tesis doctoral, a los 22 años, en la Universidad de Gottinga, propuso una prueba de que cada ecuación algebraica tiene al menos una raíz o solución.
Es decir, demostró de forma completa el teorema fundamental del álgebra.
Este teorema fundamental del álgebra había sido un desafío para los matemáticos durante siglos.
E incluso matemáticos notables como Al-Khwarizmi, Descartes, Euler, Lagrange y Laplace, por mencionar algunos, intentaron demostrarlo, pero es a Gauss, a quien se le concede el crédito de la primera demostración completa.
Este teorema se convirtió en una obsesión y continuó aportando nuevas demostraciones, por cierto, la última de cuatro la plasmó en un artículo en 1849.
También tuvo interés por estudiar la teoría de errores, dedujo la curva normal de la probabilidad, hoy conocida como la curva de Gauss.
Realizó su aporte al teorema fundamental de la aritmética. El resultado de este teorema apareció en los Elementos del gran Euclides, en el año 300 antes de nuestra era, pero su prueba estaba incompleta.
En el año 1801 publicó la formulación definitiva en su obra llamada Disquiciciones aritméticae.
Este libro lo escribió en latín y lo dedicó a su mecenas, el duque Ferdinand. Siempre sintió mucho respeto y agradecimiento hacia él por todo el interés y apoyo que le brindó.

Observa en qué consiste a través de un ejemplo:
Considera el número 1 155.
Este número se puede escribir como el producto de 5 por 231
o también como el producto de 7 por 165,
o a lo mejor como el producto de tres factores, por ejemplo: 3 por 7 por 55,
o como el producto de 4 factores: 3 por 5 por 7 por 11.
Y en esta última factorización puedes notar que todos sus factores, a diferencia del resto de las factorizaciones, son números primos: 3, 5, 7 y 11.

Así, leyendo de nuevo el teorema fundamental de la aritmética se comprueba que cualquier número entero mayor que uno, como el número 1 155, se puede descomponer como el producto de números primos, en este caso, son 3, 5, 7 y 11, y además, de manera única.
Debes de tener presente que un número primo es aquel que sólo puede dividirse por la unidad y por él mismo.
Así, los números primos son 2, 3, 5, 7, 11, 13, 19, entre otros.
Realiza el siguiente ejercicio. El número es 980. Comienza a dividirlo por los primeros números primos.
¿Es posible dividirlo entre 2? La respuesta es: sí. Entonces se coloca el dos del lado derecho y el resultado de dividir 980 entre dos, se coloca del lado izquierdo debajo del 980, es decir, 490.
Ahora, ¿se puede dividir el 490 entre 2? Y como la respuesta vuelve a ser sí, se coloca el dos del lado derecho, y el 245, del lado izquierdo.
¿Se puede dividir el 245 entre el número primo 2? Considera el criterio de divisibilidad entre 2 y no es un número par, en esta ocasión, la respuesta es no.
Continúa tratando de dividir el 245 por el siguiente número primo: 3, nota que la división por 3 no es un número entero, por lo tanto, continúa. Divide el número 245 por 5 y observa que sí es divisible.
Se anota el 5 del lado derecho, y el 49, del lado izquierdo.
Evidentemente el 49 no es divisible por 5, se continúa con el siguiente número primo: 7 y, como 49 sí es divisible por 7, se escribe 7 del lado derecho y otro 7 del lado izquierdo.
Finalmente, el 7 es divisible por 7, se coloca el 7 del lado derecho y el 1 del lado izquierdo.
Así se concluye la factorización. Ahora comprueba que el número natural 980, el cual es mayor a 1, se puede escribir como el producto de sus factores primos: 2 por 2 por 5 por 7 por 7 igual a 980.
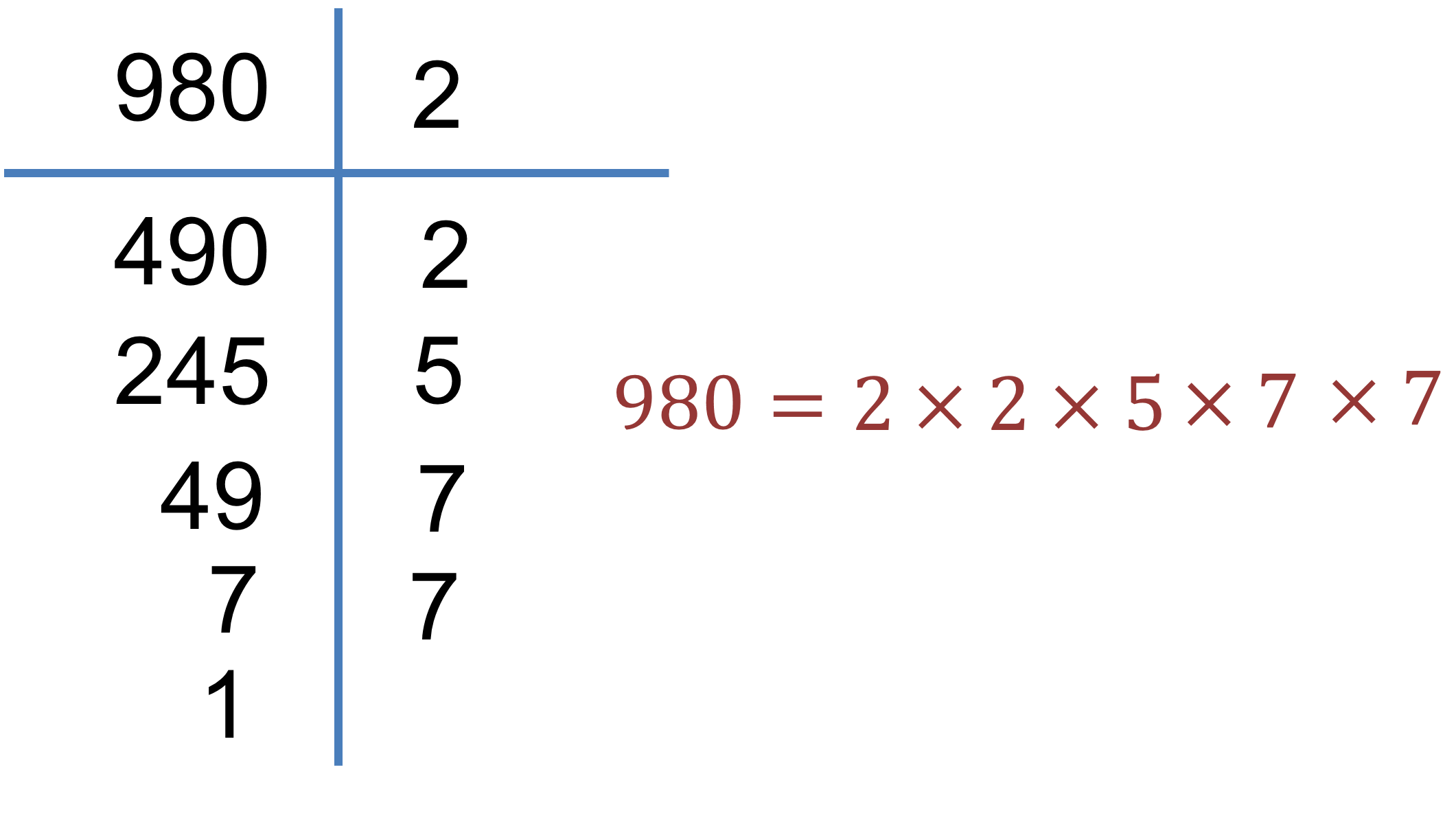
Este es el teorema fundamental de la aritmética.
Gauss dijo: “La matemática es la reina de las ciencias y la aritmética es la reina de las matemáticas”.
Se sabe que sus contribuciones a las matemáticas se extendieron a otros campos de la ciencia, como la astronomía.
Al inicio de esta sesión leíste sobre como Gauss, siendo un joven de 24 años, logró determinar la posición exacta del objeto que en su tiempo era considerado un planeta, el cual luego cambió a ser considerado un asteroide y, finalmente, hoy en día se le considera como una nueva categoría de objetos del sistema solar, llamada planetas enanos, se refiere a Ceres.
Ese pequeño astro le produjo una gran satisfacción y lo hizo muy famoso en ese tiempo. Logró determinar su trayectoria y posición exacta en el firmamento y utilizó un método llamado ahora de mínimos cuadrados.
De esta manera, el astrónomo húngaro-alemán Franz von Zach y su equipo decidieron utilizar los resultados de sus cálculos y, dirigiendo sus telescopios al lugar indicado por su matemática, encontraron sorprendidos al pequeño astro Ceres.
La astronomía le dio la oportunidad de aplicar sus propias herramientas matemáticas logrando participar de manera destacada en el nacimiento de la astrofísica.
En 1807 fue nombrado director del observatorio y profesor de astronomía en la Universidad de Gotinga.
Debió ser magnífico para los astrónomos del mundo tener las herramientas para poder predecir posiciones, no sólo de asteroides, sino también de otros cuerpos del sistema solar.
Se sabe que sus aportaciones, principalmente en el campo de las matemáticas, son extraordinarias, y debido a tan importante trabajo, ha sido merecedor, primero de toda la admiración de los matemáticos y científicos, y luego de varios reconocimientos.
Dado el gran reconocimiento a Gauss, su rostro fue plasmado en los últimos billetes de 10 marcos en Alemania antes de la entrada del euro.
Unas de sus frases:
“La matemática es la reina de las ciencias y la aritmética es la reina de las matemáticas.”
Y es considerado el “Príncipe de las Matemáticas”.
Con el trabajo del matemático Gauss has aprendido sobre las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.
El reto de hoy:
En tu libro de texto de Matemáticas puedes encontrar problemas relacionados con el teorema fundamental de la aritmética, con los números primos, así como la construcción con regla y compás de polígonos.
¡Buen trabajo!
Gracias por tu esfuerzo.
