Eventos mutuamente excluyentes e independientes II
Eventos mutuamente excluyentes e independientes II
Aprendizaje esperado: explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes.
Énfasis resolver problemas que impliquen eventos mutuamente excluyentes e independientes.
¿Qué vamos a aprender?
Los materiales que necesitarás son cuaderno, lápiz y una goma.
Anota en tu cuaderno cualquier idea o inquietud que surja al resolver las situaciones que se estudian.
Repasa algunos conceptos básicos.
La probabilidad mide la frecuencia con la que ocurre un resultado en un evento; esta medida puede expresarse en porcentaje, fracción o en decimales. Pero ¿qué se entiende por evento?
Se entiende por evento lo que puede resultar cuando se lanza un dado, o una moneda, o cuando se saca una esfera de una tómbola.
Un evento es uno o más de los posibles resultados de un experimento.
Por ejemplo, en una rifa, cuando compras algunos boletos, ¿qué probabilidad tienes de ganar?
La probabilidad se acerca al 100 por ciento, quiere decir que es muy probable que ocurra. Pero si se acerca al 0 por ciento, es poco probable que suceda.
Así que, entre más boletos compres es más seguro que ganes. Este ejemplo lo desarrollarás más adelante.
De este modo sabrás si se hace bien comprar muchos boletos para la rifa.
Conocerás a qué se refieren cuando se habla de eventos mutuamente excluyentes, y a qué con eventos independientes.
¿Qué hacemos?
Son dos o más eventos son mutuamente excluyentes si, al ocurrir uno de ellos, se excluye la posibilidad de que ocurra el otro.
De este modo, los eventos no pueden ocurrir al mismo tiempo.
Se comprueba lo anterior con el siguiente ejemplo:

Si se lanza una moneda y cae águila, ya no puedes obtener sol.
Por ese simple hecho, te puedes dar cuenta de que son eventos mutuamente excluyentes, ya que cuando ocurre uno, elimina la posibilidad de obtener el otro.
Si al lanzar un dado cae el número 2, ¿puede caer al mismo tiempo el número 6?
No, porque no puede ocurrir una y otra condición al mismo tiempo.
Esta condición lo refiere como un evento mutuamente excluyente.
Otro ejemplo es que, al lanzar un dado, cuando cae el número 2, está eliminando la posibilidad de que caiga el número 6 al mismo tiempo.
Dos eventos son independientes cuando los resultados del primer evento no afectan los resultados del segundo evento.
Pero ¿qué sucedería si al lanzar dos monedas al aire en ambas cayeran águila?
El lanzar la primera moneda no afecta el resultado de lanzar la segunda moneda, por lo que son eventos independientes.
Esto se comprueba a continuación.

Si al lanzar la primera moneda se desea obtener águila, sólo se obtiene un resultado favorable entre 2 resultados posibles.
Lo mismo ocurre para el segundo lanzamiento de moneda: si se desea obtener nuevamente águila, se aplica la misma condición porque sólo se obtiene 1 entre 2 resultados posibles.
Sin embargo, se destaca de nueva cuenta que se deben observar todas las posibilidades para cada evento.
Analiza un nuevo evento.
¿Cuáles son las posibilidades que se tienen al lanzar ambas monedas?
Que en el primer lanzamiento caiga en una moneda sol y en la otra águila.
Que caiga en ambas monedas sol.
¿Existe alguna otra posibilidad?
Caso contrario, que en ambas monedas caiga el águila.
Y una más es que en una moneda te caiga águila y en la otra te caiga sol.
y entonces sí, ya serían todas las posibilidades.
Con lo anterior, se verifica si el dato que se encontró es el correcto.
Se menciona que, al lanzar las dos monedas se obtiene:
Sol y águila
Sol y sol
Águila y águila
Águila y sol
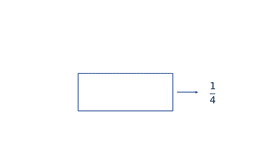
Es decir, que, para el evento, la probabilidad es uno de cuatro resultados posibles.
Se toma en cuenta que la probabilidad de que un evento ocurra es igual al número de posibilidades favorables entre el número total de posibilidades.
¿A cuánto equivale en porcentaje la fracción “un cuarto”?
Para sacar un porcentaje se divide el numerador entre el denominador; para este caso es dividir 1 entre cuatro. Se obtiene 0.25 y al multiplicar por 100 se obtiene que es igual a 25 por ciento.
A continuación, se presentan diferentes situaciones sobre eventos mutuamente excluyentes.
Situación 1
Se tienen los siguientes eventos; determinar la probabilidad en cada uno de ellos.
Se tienen 6 libros de distintas asignaturas: Historia, Lengua Materna, Biología, Matemáticas, Física e Inglés.
Si se toma uno de los libros, ¿cuál es la probabilidad de que sea un título de Biología o de Historia?
Para este caso, se toma en consideración que son seis libros en total, y que el evento es mutuamente excluyente.
De ser así, se comprueba a continuación.

Se tienen dos eventos:
Evento A: Elegir un libro de Biología.
Evento B: Elegir un libro de Historia.
Para este caso sólo hay una posibilidad para que el libro que se elija sea el de Biología; lo mismo ocurre con el libro de Historia. Y en cada caso es una posibilidad entre otras 6.
Entonces, ¿cuál es la probabilidad de que éste sea de Biología o de Historia?
Como el evento A, que implica sacar el libro de Biología es igual a un evento favorable de 6 eventos posibles. De este modo, la probabilidad es de un sexto.
Y para el evento B, que es sacar el libro de Historia, es igual a un evento favorable de 6 eventos posibles. Por lo que su probabilidad también es de un sexto.
El segundo ejemplo:
Se sabe que un dado tiene 6 caras y está enumerado del 1 al 6. ¿Cuál es la probabilidad de que al lanzarlo caiga un número par o impar?
Llamarás A y B a los dos eventos posibles.

El evento A es en el que se obtenga un número par.
Menciona cuáles son los resultados favorables.
2, 4 y 6, que son los números pares.
Entonces, se hace notar que la probabilidad del primer evento consiste en que salga un número par; se tienen 3 eventos favorables de 6 eventos posibles, por lo que corresponde a 3 sextos. Si se simplifica, equivale a un medio.
Y después, del evento B, se obtiene un número impar.
¿cuáles son los resultados favorables?
Los números impares: 1, 3 y 5.
Así para el segundo evento se tienen el 1, 3 y 5 indicando tres eventos favorables de 6 eventos posibles, por lo que la probabilidad también es igual a “un medio”.
Estos son eventos mutuamente excluyentes, porque si se obtiene un número par, se elimina la posibilidad de extraer un número impar.
Siguiente evento:
Un juego de dominó tiene 28 fichas, ¿cuál es la probabilidad del evento A, de extraer la mula? ¿Y cuál es la probabilidad del evento B, de no extraer mula?
La mula es la pieza que tiene en ambos lados el mismo número, como puede ser 1,1 o 5,5.
¿a qué tipo de evento se refiere?
Es un evento mutuamente excluyente.
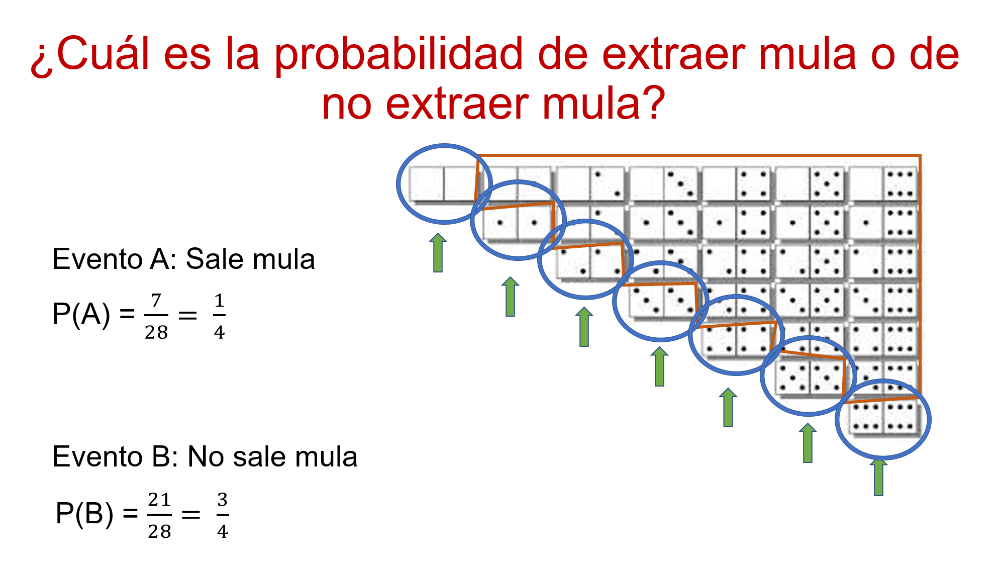
Al igual que en la situación anterior, se trata de eventos mutuamente excluyentes, porque si sale mula elimina la posibilidad de que no caiga mula.
¿Cuáles son los eventos favorables al evento A, para extraer una mula?
Son: (0,0), (1,1), (2,2), (3,3), (4,4), (5,5) y (6,6).
Entonces, para el evento A, los elementos favorables son 7 de 28 eventos posibles.
Ahora bien, para el evento B, que corresponde a que no salga mula.
¿Cuáles son los eventos favorables para este evento?
Son todas las demás fichas.
Efectivamente, por lo que para el evento B, que es igual a que no salga mula, son 21 eventos favorables de 28 eventos posibles. Es decir, igual a 21 veintiochoavos, que simplificado es igual a 3 cuartos.
Esto quiere decir que existe mayor probabilidad de extraer una ficha que no sea mula.
Si se comparan las fracciones que se obtienen en ambos eventos, para el evento A es de “un cuarto”, y para el evento B es de “tres cuartos”, lo que determina que el evento A sea mayor.
A continuación, se plantean situaciones relacionadas con eventos independientes.
Situación 2
Se tienen los siguientes eventos; determinar la probabilidad en cada uno de ellos.
- Se tienen dos juegos de dominó. Si ya se sabe que el juego tiene 28 fichas, ¿cuál es la probabilidad de extraer en el primer juego la ficha (3,5), y en el segundo extraer la ficha (6,2)?
Se trata de eventos independientes. En cualquiera de los dos eventos no se tienen elementos comunes en los posibles resultados porque, al sacar una ficha de un juego de dominó, no se altera la ocurrencia para la obtención de otra en el segundo juego de fichas.
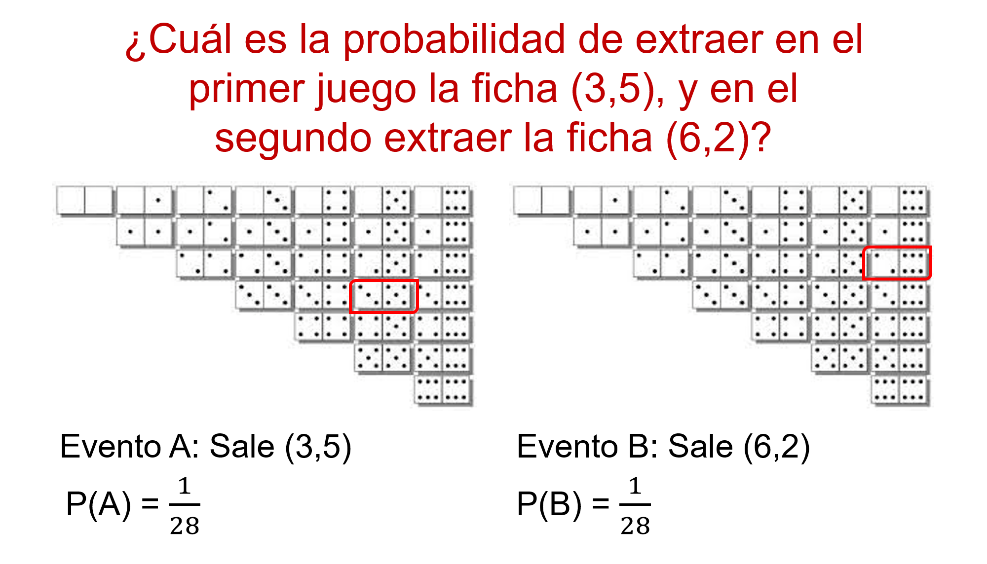
Cualquiera de las fichas tiene la misma probabilidad de ocurrencia, es decir, en cualquiera de ellas la probabilidad del evento es de un veintiochoavo.
La probabilidad del evento A de obtener la ficha (3,5) es igual a 1 de 28.
Por otro lado, la probabilidad del evento B de obtener la ficha (6,2) también es igual a 1 de 28.
En ambos no afecta la probabilidad de que suceda un evento u otro.
Siguiente ejemplo. Leslie compró boletos para una rifa.
La rifa es de su mi amiga. Ella le dijo que eran 20 boletos en total y Leslie le compro 5 boletos; los números que escogió son: 8, 9, 10, 11 y 12. Sé meterán todas las esferas numeradas del 1 al 20 en una tómbola, y gana el primer número que salga. La pregunta es: ¿qué posibilidad tiene de ganar?
Para responderlo, se desarrolla el problema.
Otro dato importante es que su hermano de Leslie también compró 5 boletos y él asegura que saldrá ganador; esto lo dice porque pidió los números 2, 6, 14, 18 y 20, y argumenta que tiene más posibilidades de ganar porque los números que escogió están mejor distribuidos entre el total. Sin embargo, Leslie piensa que tiene las mejores posibilidades de ganar porque sus números son seguidos.
Plantea la situación del ejercicio.
La rifa consta de 20 boletos, para lo cual se utiliza una tómbola con esferas numeradas del 1 al 20. El boleto ganador será el primero que se saque de la tómbola.
Leslie compró 5 boletos y su hermano también compró 5 boletos.
Leslie escogió los números 8, 9, 10, 11 y 12, y su hermano los números 2, 6, 14, 18 y 20.
Ahora bien, lo que Leslie desea saber es: ¿qué probabilidad tiene de ganar y qué probabilidad tiene su hermano? También quiere saber quién de ellos tiene la mayor probabilidad de ganar.

El evento A es el de Leslie, y su probabilidad es igual a 5 boletos, que son los resultados favorables entre 20 resultados posibles, que son los 20 números de la rifa.
Para su hermano, que es el evento B, la probabilidad es igual a 5 resultados favorables, entre los 20 resultados posibles.
En consecuencia, tanto para Leslie como para su hermano, la fracción es igual a 5 veinteavos, que simplificado se obtiene que es igual a un cuarto.
En ambos casos, cada boleto independientemente del número que represente, tiene la misma probabilidad de ganar.
Ahora bien, ¿a qué porcentaje equivale esa probabilidad?
Para obtener en forma de un porcentaje se divide el numerador entre el denominador. Para este caso, será dividir 1 entre cuatro, 0.25, y si se multiplica por 100 es igual a 25 por ciento.
Tanto su hermano como ella tienen las mismas probabilidades para conseguir el premio de la rifa, es decir, un 25 por ciento.
Pero ¿de qué tipo de evento se trata? ¿Es un evento mutuamente excluyente o es un evento independiente?
Se trata de un evento mutuamente excluyente porque es una sola extracción de la esfera con un número. De este modo, si saliera la esfera del número 10 ya no podría salir ninguna otra esfera ganadora, pues esa sería la premiada.
Retoma lo aprendido durante la sesión:
Se plantearon ejemplos tanto de eventos mutuamente excluyentes como independientes.
De este modo, se resolvieron situaciones con eventos mutuamente excluyentes e independientes, y se analizaron las diferencias entre estos dos eventos.
Por un lado, se dice que dos o más eventos son mutuamente excluyentes si, al ocurrir uno de ellos, excluye la posibilidad de que ocurra el otro.
Mientras que dos eventos son independientes cuando los resultados del primer evento no afectan los resultados del segundo evento.
Ten presente lo trabajado en la sesión y así aplícalo en diferentes casos.
El reto de hoy:
Si se lanza una moneda cuatro veces consecutivas y en todas ellas cae águila, ¿cuál es la probabilidad de que en el quinto lanzamiento de la moneda también caiga águila?
¿Se trata de un evento mutuamente excluyente o de un evento independiente?
En tu libro de texto tiene ejercicios similares para resolver problemas que impliquen eventos mutuamente excluyentes e independientes. Es importante que con estos practiques lo aprendido.
Una frase Albert Einstein: “Nunca consideres el estudio como una obligación, sino como una oportunidad para penetrar en el bello y maravilloso mundo del saber”.
¡Buen trabajo!
Gracias por tu esfuerzo.