Eventos complementarios. Problemas
Eventos complementarios. Problemas
Aprendizaje esperado: explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: resolver problemas que impliquen eventos complementarios.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno de matemáticas, lápiz y goma, es muy importante que tomes nota de cada una de las dudas que surjan durante el desarrollo de la sesión para que puedas compartirlas con tus compañeras, compañeros y profesores.
Es importante recordar algunos conceptos.
- Espacio muestral
- Evento o suceso
- Conteo de resultados
- Eventos complementarios
¿Qué hacemos?
Primero, debes saber que el espacio muestral se considera al conjunto de todos los resultados posibles en un experimento aleatorio, por ejemplo, al lanzar una moneda su espacio muestral es sol o águila, ya que son los únicos resultados posibles y los representas con la letra S mayúscula.
Ahora, asocia el espacio muestral a otro experimento aleatorio: lanzar un dado ¿Sabes cuál es su espacio muestral? ¿Cuáles son los únicos resultados posibles al lanzar un dado?
Son, 1, 2, 3, 4, 5 y 6.
Ahora, observa lo que es un evento o suceso. Es un conjunto de posibles resultados que se pueden dar en un experimento aleatorio, pero ¿qué es eso? Regresa a tu dado, y a tu espacio muestral, un evento podía ser “obtener un número menor a 3”.
Si observas, el evento describe una o varias características de los resultados posibles en el espacio muestral, por lo que sólo se seleccionan parte de los resultados, en este caso el 1 y el 2, ya que son los únicos valores que cumplen con este requisito.
Observa los resultados posibles de un evento, en este otro experimento: lanzarás una moneda al aire en dos ocasiones y te auxiliarás de un diagrama de árbol para poder representar todos los resultados posibles.
Al caer las monedas al piso, en la primera moneda sólo puedes obtener dos resultados posibles: sol o águila, en caso de caer sol en la primera moneda, en la segunda podría caer sol o águila nuevamente, y para el caso de que en la primera caiga águila, el resultado de la segunda podría ser nuevamente sol o águila.
Si observas ahora, en el primer lanzamiento sólo cae un sol o un águila, y en el segundo lanzamiento también cae un sol o un águila.
El resultado final del experimento depende del resultado de las dos monedas. Si ahora cuentas los resultados posibles observas que da un total de cuatro posibles resultados.
Dentro de este mismo experimento crea un evento: “Salen dos soles”. Si observas en el diagrama de árbol, sólo hay un resultado que cumpla con un evento solicitado. Por lo tanto, sólo es uno de tres resultados posibles.
Ahora, observa los eventos complementarios que ya conoces. Los eventos complementarios son aquellos que al ocurrir da la cardinalidad total del evento, es decir, el total de los resultados posibles, además entre ambos eventos son excluyentes entre sí, lo cual significa que no pueden ocurrir simultáneamente, por ejemplo, al lanzar una moneda no pueden caer al mismo tiempo águila o sol.
Tienes ahora una urna con seis pelotas, cuatro de color azul y dos de color rojo.
En este caso, tu primer evento, denominado M será sacar de forma aleatoria una pelota de color azul, y el evento N, el cual nos habla de obtener una pelota roja.
De esta forma, no puedes obtener una pelota roja o azul al mismo tiempo, por lo tanto, son eventos excluyentes entre sí, además como sólo tienes pelotas rojas y azules se consideran eventos complementarios, y los representas como el evento M es complementario al evento N y por consecuencia lógica el evento N es complementario al evento M, y entre los dos dan el total de la cardinalidad de los resultados posibles.
Antes de iniciar con la lección, conocerás una de las narraciones que aparece en el libro El hombre que calculaba de Malba Tahan. Cuenta la historia del tablero de ajedrez y su creador, un joven hindú llamado Lahur Sessa, para recreo de un rey de la India hace ya muchos siglos.
“Vivió y reinó hace ya muchos siglos un rey llamado Lavada dueño de la provincia de Taligana, el cual se vio en la necesidad de empuñar la espada para repeler un insólito y brutal ataque de un reino vecino”.
El choque de ambos monarcas sembró de muertos los campos. Lavada era un gran estratega militar y con ese ingenio logró vencer al enemigo y traer paz a su reino. Sin embargo, le costó la vida de muchos jóvenes, entre ellos la de su hijo, el príncipe Adjamir, quien se sacrificó en el momento culminante para dar la victoria final a los suyos.
Mientras el pueblo quería festejar, el rey se encerró en sus habitaciones a sufrir la muerte de su hijo. ¿De qué le servía la victoria, los ricos palacios, los tesoros inmensos si la razón de su existir había desaparecido?
Sobre una caja de arena revivía la estrategia que le había llevado a ganar. Una y otra vez repetía la batalla.
Todos los brahmanes elevaban oraciones por el desgraciado rey. Hasta que un día se presentó al palacio un joven llamado Sessa. Llevado por la noticia de la terrible tristeza del rey, pensó en inventar un juego que pudiera distraerlo y abrir su corazón a grandes alegrías. Al oír esto el rey lo hizo pasar y él les mostró un tablero cuadrado dividido en sesenta y cuatro cuadritos iguales, en él se colocaban dos colecciones de piezas que se distinguían unas de otras por el color, blancas y negras, repetidas simétricamente y subordinadas a reglas que permitían de varios modos sus movimientos.
El joven Sessa enseñó al rey, a los visires y a varios cortesanos en qué consistía el juego, enseñándoles sus reglas esenciales, los movimientos de cada pieza y la representación de cada una en el campo de batalla.
El rey interesado aprendió a mover las piezas con tal habilidad que derrotó a todos sus contrincantes, y pudo percibir que podía reproducir la batalla mejor que en su caja de arena.
Descubrió que para poder ganar en ocasiones hay que sacrificar una pieza importante, como lo fue la pérdida de su hijo en la batalla para obtener el triunfo. Este conocimiento ayudó al rey a superar su profunda tristeza.
Decidido a premiar a Sessa, le llamó para preguntarle el precio por su atinado juego. El modesto joven le indicó que con su recuperación era más que suficiente. No obstante, el rey insistió e insistió hasta que Sessa le pidió que le entregara sólo granos de trigo. El rey le reclamó que pudiendo pedir grandes tesoros, palacios y riquezas, él sólo pedía granos de trigo, a lo cual accedió. Sin embargo, había una condición: “Dadme un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta y así duplicando sucesivamente la cantidad, hasta la sexagésima cuarta y última casilla del tablero”.
Todos en la sala rieron estrepitosamente y el rey ordenó que le entregaran tan insignificante cantidad de granos de trigo, pidió a los calculistas del reino realizaran las operaciones necesarias y le entregaran su saco de trigo.
Los sabios matemáticos del rey volvieron algunas horas después de profundos estudios para dar a conocer al rey la cantidad solicitada y le dijeron: ‘Calculamos el número de granos de trigo que hay que entregarle al joven Sessa y obtuvimos un número cuya magnitud es inconcebible para la imaginación humana, de tal forma que la India entera, sembrados todos sus campos, y destruidas todas sus ciudades para sembrar no se produciría en un siglo la cantidad de trigo que, por vuestra promesa, debe entregarse al joven Sessa.
El asombrado rey no daba credibilidad a lo que escuchaba, sin poder cumplir su promesa invitó al intrépido joven a ocupar el puesto en la corte como su primer ministro”.
¿Qué tan grande es la cantidad que prometiera el rey al joven Sessa? La primera casilla matemáticamente la podrías representar con un dos elevado a la primera potencia, lo que da como resultado uno, la segunda con un dos elevado a la segunda potencia, lo que da el dos. La tercera casilla con un dos elevado al cubo. La cuarta con dos elevado a la cuarta potencia y así sucesivamente hasta llegar a la última casilla en donde la cantidad resultante sería dos elevado a la potencia sesenta y cuatro.
¿Y qué tanto trigo sería? En la actualidad, si consideras la producción mundial de trigo por un año y la almacenáramos toda, tardaríamos más de mil años en reunir la cantidad pedida por el joven Sessa.
Después de escuchar la historia del juego de ajedrez, continua con el tema de eventos complementarios, pero utilizarás este brillante juego como base para buscar en él ejemplos de eventos complementarios.

Inicia con el tablero, si consideras que tiene la forma de un cuadrado, y empieza en uno de sus lados dividiéndolo en partes iguales y al contarlas encuentras que son cinco, seis, siete y ocho de estos cuadros en la primera línea y si sigues colocando estos cuadros para formar líneas y además los intercalas según su color observa, seis, siete y ocho filas en total. Si procedes a hacer el conteo de cuadros encuentras que el total es de 64 casillas existentes; por lo tanto, la cardinalidad del tablero es de 64. Ahora, si observas que algunas son blancas y otras de color negro y realizas el conteo por color encuentras que el total de casillas blancas es exactamente la mitad de la cardinalidad, es decir, 32 casillas blancas y el conjunto contrario que es de color negro también representa la mitad de éste.
Llegas a la conclusión de que, entre ambos conjuntos, las casillas blancas más las casillas negras dan el total del tablero.
Además, si tomas en cuenta que las casillas blancas no pueden ocupar las casillas negras de forma simultánea, encuentras la descripción perfecta de un evento complementario, es decir, son excluyentes entre sí y entre las dos dan el total de los resultados.
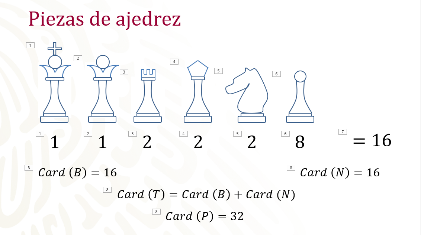
Como las piezas sólo pueden ser de color blanco o negro y no pueden ser de los dos colores de forma simultánea, puedes decir que son excluyentes entre sí; además, entre los dos colores dan el total de las piezas y puedes deducir que éste sería otro ejemplo de un evento complementario.
Observa ahora con el movimiento de las piezas de acuerdo con su papel dentro del juego, cada una de ellas se desplaza según sus propias reglas.
Existen dos reyes en el juego, así como cuatro caballos y dieciséis peones. Estas piezas tienen un avance limitado de casillas, ya que sólo se les permite avanzar una o un número establecido de éstas. Mientras que las cuatro torres, los cuatro alfiles y las dos reinas pueden avanzar tantas casillas como sean necesarias. La forma en la que avanzan entre estos dos grupos de piezas no puede cambiarse ni usurpar el avance de otras piezas, por lo que se consideran excluyentes entre sí.
Al sumar el total de las piezas con avance limitado y las que tienen avance sin límite, obtienes el total de las piezas que integran el ajedrez y las puedes considerar como complementarias.

Y ya que se habla de avances limitados y sin límites es importante mencionar que hay un tipo de pieza que puede cambiar su función. Ésta es el peón, el cual, si logra recorrer todo el tablero de un extremo al otro, puede ser cambiado por cualquier otra pieza del juego de ajedrez. Puedes decir entonces que sólo 16 de estos pueden cambiar su función, mientras tanto los dos reyes, las dos reinas, los cuatro alfiles, las cuatro torres y los cuatro caballos no pueden cambiar nunca de función.

Este cambio las hace excluyentes entre sí y además si las sumas dan el total de piezas del juego de ajedrez, por lo que se podrían considerar como complementarias.
Antes de empezar es necesario acomodar las piezas según las reglas preestablecidas del juego. Sabes que se tienen un total de 64 casillas, procede a dividir las piezas por color, y las colocas en las dos primeras líneas del lado de cada jugador.
Nota que para un color se ocupan 16 casillas y para el otro color otras 16 casillas, por lo tanto, el total de cuadros ocupados es de 32, lo que deja 32 casillas vacías para poder realizar movimientos. Si sumas ambas cantidades obtienes el total de casillas del juego, entre las casillas ocupadas y las casillas vacías son excluyentes entre sí al principio del juego, y complementarias entre sí, ya que dan el total del conjunto.
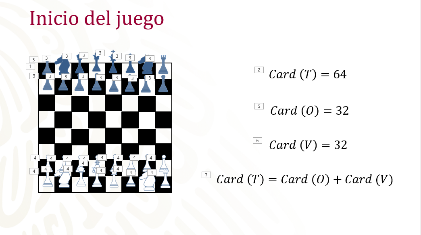
Hasta ahora has utilizado el juego de ajedrez para que puedas percibir las características de los eventos complementarios, los cuales son excluyentes entre sí y la suma de ambos es igual al total de los resultados.
En la vida cotidiana existen muchos ejemplos donde usas los eventos complementarios, observa algunos de ellos:
En algunas escuelas secundarias del país, cuando los estudiantes entran a primero de secundaria, la asignación de grupos se hace al azar, es decir, de forma aleatoria. Analiza ahora la posibilidad de que como estudiantes te toque en un grupo al cual quieras pertenecer.
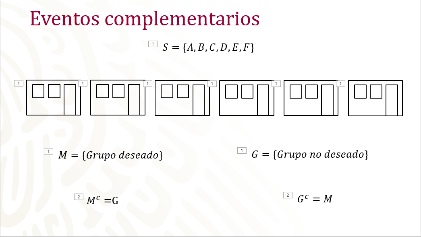
Piensa que quieres estar en el último grupo, por ejemplo, cuando entras a la secundaria, ésta tiene seis grupos, y los nombran con letras de la “A” a la “F”, ¿qué posibilidad tendrías de que te tocara el grupo que quieres?
Construye primero el espacio muestral, el cual se representa con la letra S y debe contener todas las posibilidades en las cuales puedes quedar asignado, es decir, los grupos que tiene la escuela a la cual estas inscrito y que en este caso son seis. Son seis posibilidades y tu deseas una de ellas. Al evento que representa tu deseo lo vas a denominar con la letra M y lo expresas matemáticamente como el evento M y el otro evento lo denominarás G, el cual representa los otros grupos que no deseas. Si observas ambos eventos no pueden ocurrir simultáneamente, ya que no puedes quedar asignado a dos grupos distintos, por lo tanto, puedes considerar que ambos eventos son excluyentes entre sí, ya que no podrían ocurrir al mismo tiempo, por otro lado, en el grupo que deseas es más difícil que quedarte en cualquiera de los otros. Es decir, es más fácil que ocurra el evento G que el evento M.
Matemáticamente puedes expresar que el complemento del evento M es el evento G, y el complemento del evento G es el evento M.
Como acabas de observar, con este ejemplo encuentras eventos complementarios en una situación de la vida cotidiana.
Otro ejemplo: Una amiga juega futbol soccer. En el partido de hoy todos esperan que anote un gol, y aunque sabes que existen muchos factores que determinan la forma en que un gol se anota y que se refiere a un trabajo de equipo, al final el que tira a la portería para anotar en la mayoría de las veces es una sola persona. ¿Cuál es la posibilidad de que mi amiga anote un gol?
Para empezar, ella tiene la posición de delantero, es decir que son los que tienen el mayor número de oportunidades de anotar un gol; además, en el equipo en donde juega, sólo hay tres jugadoras con esa posición. Si planteas que el primer gol caerá anotado por una de ellas, ¿cuál sería la posibilidad de que ella anote?
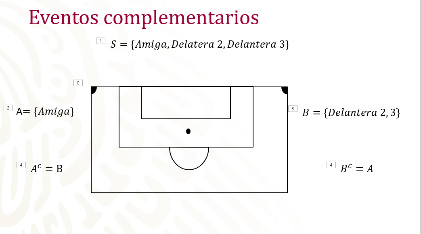
Si observas el espacio muestral, se encuentran las tres personas que tienen la posición de delantero en el equipo.
El evento A sería la anotación hecha por mi amiga y el evento B corresponde a una persona diferente, en este caso las otras dos jugadoras
Si observas la cantidad de oportunidades para anotar que tienen otras personas en comparación a las oportunidades de mi amiga, podrías decir que ambos eventos son complementarios, ya que no ocurren al mismo tiempo y suman todas las oportunidades de las jugadoras que juegan en la posición de delantero.
Mientras el evento A tiene una cardinalidad de 1, el evento B tiene una cardinalidad de 2; por lo tanto, mi amiga tiene menos posibilidades de anotar el gol.
Matemáticamente hablando puedes expresar que el evento complementario de A es el evento B y el evento complementario de B es el evento A.
Otro ejemplo: todos los días al salir de la escuela pasan cuatro camiones diferentes en la avenida para ir a casa; no vienen al mismo tiempo, según el tráfico, la hora de salida, entre otros factores. ¿Qué posibilidad tienes de que el día de mañana me toque el mismo camión que el día de hoy
Si observas bien, el espacio muestral está conformado por los 4 camiones, los cuales se han numerado del uno al cuatro, tienes el evento “X” que es el mismo camión que el día anterior, y el evento “Y” representa un camión diferente. La cardinalidad del evento “X” es de uno y la cardinalidad del evento “Y” es de tres; por lo tanto, las posibilidades de que te subas nuevamente al camión del día anterior son menores, ya que son tres contra uno.
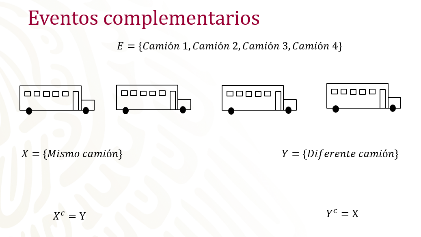
Si observas son eventos excluyentes entre sí, ya que no te puedes ir en dos camiones al mismo tiempo, y si sumas la cardinalidad total obtienes el total del espacio muestral.
Representa, matemáticamente hablando, cómo el complemento de “X” es “Y” y el complemento de “Y” está representado por “X”. Para finalizar te sugerimos anotar las características de los eventos complementarios, son excluyentes entre sí y la suma de sus elementos siempre será el total del espacio muestral.

En caso de que tengas eventos excluyentes entre sí, es decir, que no puedan ocurrir al mismo tiempo y que la suma de su cardinalidad sea menor al espacio muestral, no se consideran eventos complementarios. Otra característica de los eventos complementarios es que un evento niega la posibilidad del otro, si lanzas una moneda al aire sabes que al caer sol automáticamente no puede caer águila.
El reto de hoy:
Serán dos retos, el primero es que busques eventos complementarios en tu día a día, y el segundo, que busques en tu libro de texto ejercicios para que refuerces tus conocimientos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más.