El metro, sus múltiplos y submúltiplos
El metro, sus múltiplos y submúltiplos
Aprendizaje esperado: resuelve problemas que implican conversaciones en múltiplos y submúltiplos del metro, litro, kilogramo, y de unidades del sistema inglés (yarda, pulgada, galón, onza y libra).
Énfasis: resolver problemas que implican conversaciones en múltiplos y submúltiplos del metro.
¿Qué vamos a aprender?
En esta sesión estudiaras el metro, unidad de longitud del Sistema Internacional de Unidades. También aprenderás sobre los múltiplos y submúltiplos de esta unidad.
¿Qué hacemos?
Situación-problema.
El maestro de Leonardo le pide medir la distancia que recorre de su casa a la escuela. Esto provoca en Leonardo curiosidad, y se pregunta:
¿Para qué medir?
Para responder, analiza lo que es una magnitud y una medida.
La Oficina Internacional de Pesas y Medidas, por medio del Vocabulario Internacional de Metrología, define la magnitud como:
Magnitud
La propiedad de un fenómeno, cuerpo o sustancia, que puede expresarse cuantitivamente mediante un número y una referencia.
En este caso, la longitud es la magnitud que estamos definiendo.
Entonces, para medir magnitudes, nos apoyamos de una herramienta a la que denominamos unidad de medida. Analiza qué es una unidad de medida.
El metro es una unidad fundamental que forma parte de un sistema consistente de unidades, llamado Sistema Internacional de Unidades, el cual se basa en siete unidades fundamentales, correspondientes a las unidades de longitud, masa, tiempo, corriente eléctrica, temperatura, cantidad de materia e intensidad luminosa.
En esta ocasión hablaremos del metro como unidad fundamental de longitud en el Sistema Internacional de Unidades, el cual se abrevia como “SI”.
El Sistema Internacional se usa en México y en muchos otros países; en otros, en cambio, se utiliza el Sistema Inglés o Sistema Imperial, incluido México.
La unidad de medida es una referencia que se usa para medir la magnitud física de un determinado objeto, sustancia o fenómeno, por ejemplo, para la longitud:
- El codo
- La vara
- La cuarta
Se emplearon para determinar medidas en tiempos antiguos. Y los más usados actualmente son: - El metro, el kilómetro y el centímetro
- La yarda, el pie y la pulgada
¿Has tenido alguna experiencia con alguna de estas unidades de medida? ¿En tu localidad se usa alguna de manera específica? De ser así, descríbela anotando sus ventajas o desventajas como unidad de medida.
Ahora concentrémonos en la unidad de medida que estudiaremos en esta sesión, que es el metro. El metro es la unidad de longitud que nos permite determinar la distancia entre dos puntos.
Algunos ejemplos de longitud son:
- La distancia entre tu casa y tu escuela.
- La distancia entre la cocina y tu habitación.
- La distancia entre un extremo y otro de una mesa.
- La distancia entre la punta de un lápiz y la goma de ese mismo lápiz.
En estos ejemplos las longitudes son comunes en nuestro alrededor, pero las longitudes pueden ser muy grandes o muy pequeñas.
¿Qué es el metro?
El metro es la unidad de longitud del Sistema Internacional de Unidades. Se utilizan múltiplos y submúltiplos para medir y expresar longitudes que sean apropiadas a su orden de magnitud.
Para ello, analiza la siguiente actividad que te permitirá reconocer la utilidad del metro y la de sus múltiplos y submúltiplos.
De acuerdo con tu experiencia y conocimientos, marca con una palomita la unidad de medida que consideres más conveniente o la mejor opción para medir las siguientes distancias y longitudes.


Piensa el porqué de la unidad de medida que has elegido y registra tu argumento.
Antes de proponer las respuestas a las preguntas anteriores, analiza qué son los múltiplos y submúltiplos del metro, y qué tipo de mediciones puedes realizar con ellos, ya que te será de utilidad para determinar cuál es la unidad más apropiada para realizar la medida en las situaciones descritas anteriormente.
¿Qué son los múltiplos y submúltiplos del metro?
Los múltiplos
Son las unidades de medida más grandes que el metro. Se utilizan para medir objetos, u otros, más grandes que el metro.
Los submúltiplos
Son las unidades de medida más pequeñas que el metro. Se utilizan para medir objetos, u otros, más pequeños que el metro.
Los múltiplos del metro hacen referencia a unidades de medida mayores que el metro.
- Generalmente se utilizan para medir objetos cuyas medidas son mayores que el metro a partir de los múltiplos de diez.
Los submúltiplos del metro hacen referencia a unidades de medida menores que el metro. - Generalmente se utilizan para medir objetos cuyas medidas son menores que el metro a partir de los submúltiplos de diez.
Es importante acotar que los múltiplos de diez son aquellos que se obtienen al multiplicar por diez las unidades de medida; los submúltiplos se obtienen al dividirlas por diez.
Con esta definición de los múltiplos y submúltiplos reflexiona acerca de su utilidad en la medición y de cómo su uso facilita el manejo de medidas y cálculos, ya que algunas veces es necesario medir longitudes muy grandes, y otras veces, muy pequeñas. En ambos casos, utilizar el metro como unidad de referencia puede dificultar su operatividad, manejo e interpretación.
Conoce ahora cuáles son los múltiplos y submúltiplos del metro.
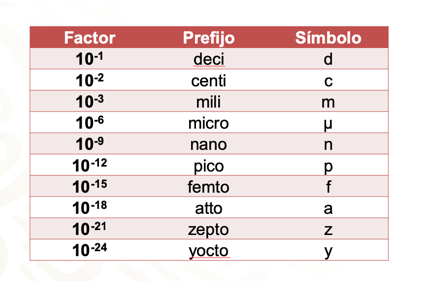
Observa la siguiente tabla, en la que aparecen los múltiplos mayores a la unidad y su equivalencia en potencias de diez: deca, hecto, kilo, mega, giga, tera, peta, exa, zetta, yotta.

Ahora observa la siguiente tabla en la que aparecen los submúltiplos menores a la unidad y su equivalencia en potencias de diez: deci, centi, mili, micro, nano, pico, femto, atto, zepto, yocto.
Los múltiplos más comunes en la vida cotidiana que se utilizan para medir longitudes mayores al metro son el decámetro, el hectómetro y el kilómetro.
- El decámetro se abrevia dam, y equivale a 10 metros.
- El hectómetro se abrevia hm, equivale a 100 metros.
- Y el kilómetro se abrevia km, equivale a 1000 metros.
Los submúltiplos del metro comunes en la vida cotidiana se utilizan para medir longitudes menores al metro y son el decímetro, el centímetro y el milímetro.
El decímetro se abrevia dm y equivale a un décimo de metro, es decir, 0.1 m (cero, punto, uno).
El centímetro se abrevia cm y equivale a un centésimo de metro, es decir, 0.01 m (cero, punto, cero, uno).
El milímetro se abrevia mm y equivale a un milésimo de metro, es decir, 0.001 m (cero, punto, cero, cero, uno).
Para los múltiplos y submúltiplos del metro, se cumple que cada unidad de longitud es 10 veces mayor (la de la izquierda) que la inmediata inferior (la de la derecha).

Ya que has analizado los múltiplos y submúltiplos del metro y la utilidad en su manejo, regresa a determinar las mejores opciones en las situaciones que se plantearon anteriormente.
Reflexiona sobre lo que tú, pensaste y determinaste como la mejor opción.
De acuerdo con lo que has analizado, marcaras la unidad que consideres más conveniente para medir las siguientes distancias y longitudes.

Inciso a: La distancia que hay de una ciudad a otra, evidentemente, es mayor que un metro; por lo tanto, es conveniente utilizar uno de los múltiplos del metro, dam, hm, km.
Observa que no sería práctico utilizar el milímetro, el centímetro o el decímetro, ya que estas unidades son submúltiplos, y considera que son útiles para medir longitudes menores al metro.
En este caso, la unidad de medida más apropiada para determinar la distancia de una ciudad a otra es el kilómetro.
Inciso b: Piensa en que pudiera ser que las casas estén una junto a la otra; puede ser que exista una casa de separación entre ellas o también podrían estar separadas de esquina a esquina de la calle, por esta razón considera que el metro es la mejor opción para determinar la distancia de separación entre dos casas.
Incluso hay lugares en nuestro país donde las casas están separadas por predios o terrenos muy grandes, y podrían haber elegido hectómetros o kilómetros.
Recuerda que la respuesta debe de dar sentido y significado dentro del contexto.
Inciso c: Este tipo de lombriz definitivamente tendrá una longitud menor al metro, por lo tanto, usaremos un submúltiplo, y la mejor opción es el centímetro.

Inciso d: Evidentemente la distancia de nuestro planeta al Sol necesita un múltiplo, ya que es una distancia mayor al metro, y por ello utilizaríamos el kilómetro.
Inciso e: El hectómetro y el kilómetro son múltiplos del metro y equivalen a 100 m y 1000 m, respectivamente, esta longitud es demasiado “grande” para lazar ganado.
Por otro lado, si utilizas el centímetro o el milímetro, submúltiplos del metro (que representan la centésima y la milésima parte del metro, respectivamente), son unidades muy pequeñas para lo que necesitas medir, por lo tanto, en este caso lo más recomendable es utilizar el metro como unidad de medida para medir la cuerda para lazar ganado.
Las situaciones anteriores te brindan un panorama acerca del uso y utilidad de los múltiplos y submúltiplos del metro al determinar medidas de longitud. Sin embargo, es importante reconocer que, en muchas ocasiones, al querer determinar una longitud, es posible expresarla en dos o tres múltiplos o submúltiplos.
Esto significa que no es determinante que una medida pueda ser expresada en una sola unidad. Por ejemplo, al medir una longitud en centímetros, ésta también puede expresarse en milímetros, o bien que alguna longitud medida en decámetros puede expresarse en metros. De aquí la importancia de reconocer las equivalencias entre múltiplos y submúltiplos del metro.
¿Qué pasaría si en cierta circunstancia se te presentaran cálculos en los que intervienen medidas dadas en centímetros y en milímetros?
Lo importante es que sean equivalentes.
Por ejemplo, para determinar el área de un rectángulo, cuya base está dada en centímetros y la altura en milímetros.
Antes de revisar situaciones de este tipo, analiza a detalle cómo puedes obtener equivalencias entre el metro y algún múltiplo o submúltiplo, o viceversa.
Para obtener la equivalencia entre un múltiplo del metro y un submúltiplo, harás uso de una tabla de datos como ésta.
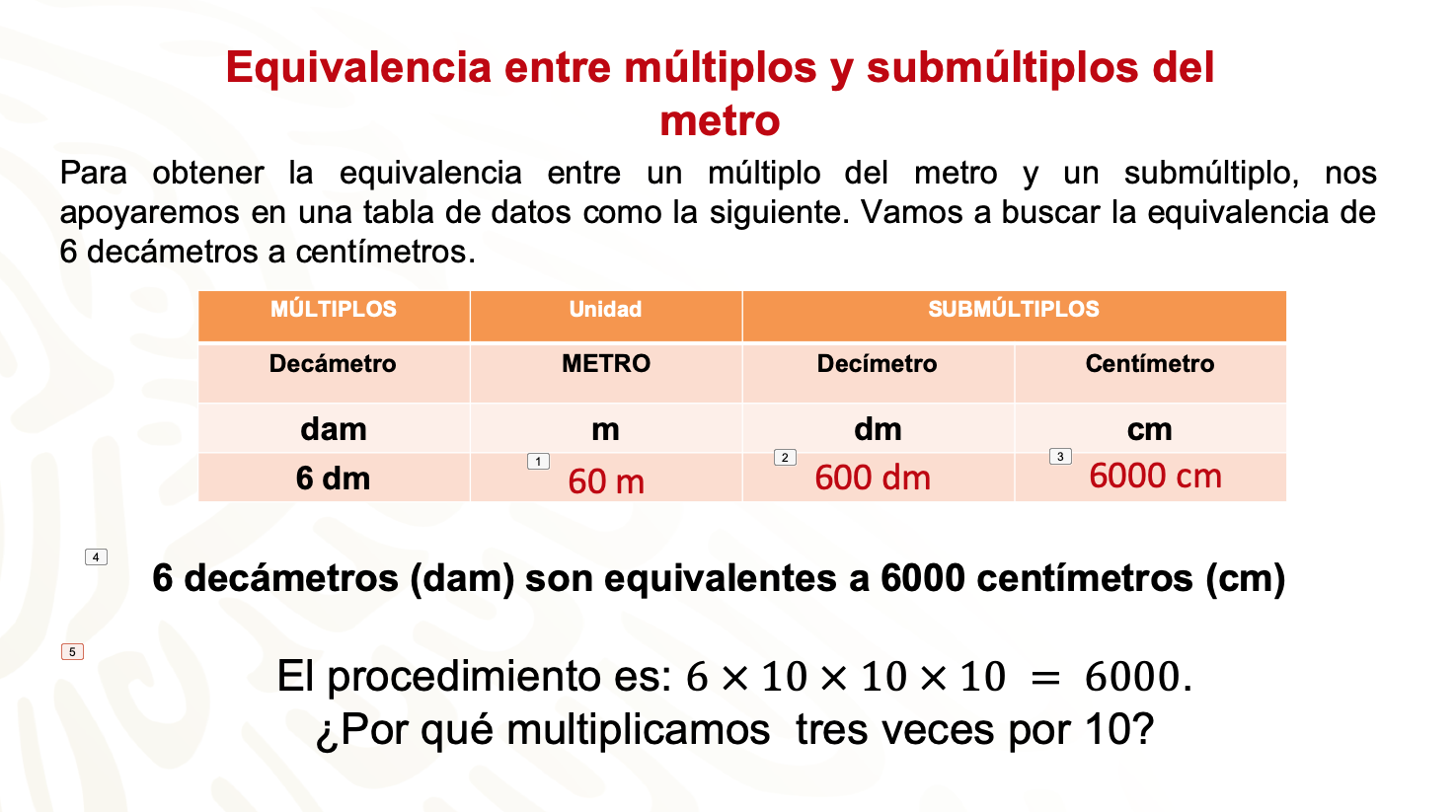
Busca la equivalencia de 6 decámetros a centímetros.
1 decámetro es equivalente a 10 metros, entonces multiplicamos 6 x 10, y tenemos 60 metros.
- 6 decámetros son equivalentes a 60 metros.
1 metro es equivalente a 10 decímetros, entonces multiplicamos 60 x 10, y tenemos 600 decímetros. - 6 decámetros son equivalentes a 60 metros, y 60 metros son equivalentes a 600 decímetros.
1 decímetro es equivalente a 10 centímetros, entonces multiplicamos 600 x 10, y tenemos 6 000 centímetros. - 6 decámetros son equivalentes a 60 metros, 60 metros son equivalentes a 600 decímetros y 600 decímetros son equivalentes a 6 000 centímetros.
Por lo tanto, 6 decámetros son equivalentes a 6 000 centímetros (cm).
Las equivalencias que has determinado se pueden obtener con el siguiente procedimiento: multiplicamos 6 x 10 x 10 x 10, que es igual a 6 000.
¿Por qué multiplicamos 6 por tres veces 10?
¿Qué piensas? ¿A qué conclusión puedes llegar?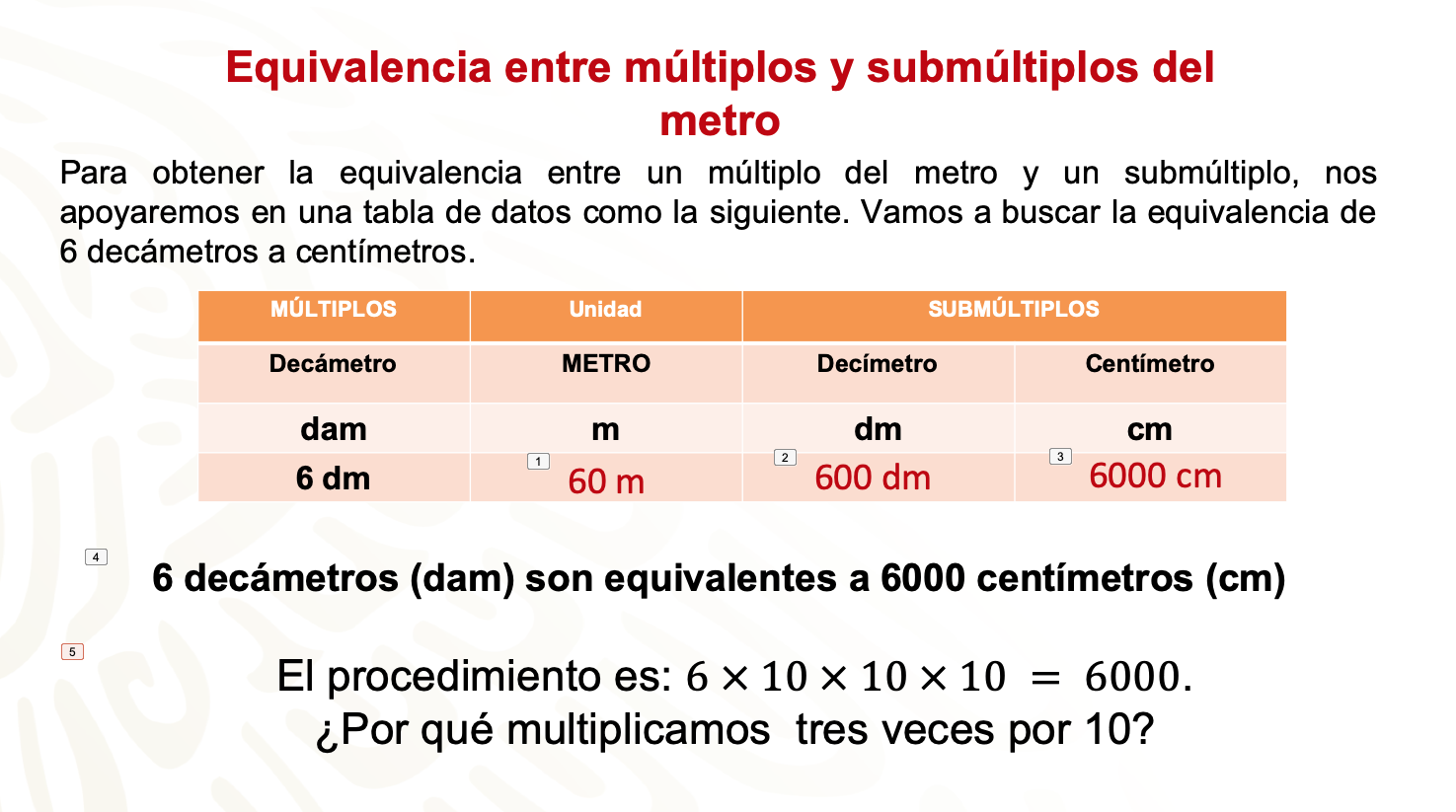
Para obtener la equivalencia entre un múltiplo del metro, en ese caso, los decámetros, y un submúltiplo, que son los centímetros, multiplica 6 por 10 para obtener su equivalente en metros. El producto se multiplica por 10 para obtener su equivalente en decímetros, el producto se multiplica por 10 para obtener su equivalente en centímetros.
Asimismo, sabes que 10 x 10 x 10 es igual a 1 000; de esta manera puedes multiplicar 6 x 1 000 = 6 000, y obtienes el mismo valor numérico.
Al calcular la equivalencia de 6 decámetros en centímetros. Considera que estamos buscando la equivalencia entre una unidad mayor con una menor.
Observa la tabla, hay tres lugares entre los dam y los cm, para encontrar la equivalencia multiplicamos 6 por 1 000, cuyo producto es 6 000.
Entonces, 6 decámetros (dam) es equivalente a 6 000 centímetros (cm).
Para obtener la equivalencia entre el metro y uno de sus múltiplos, te apoyaras en una tabla de datos como ésta. Vamos a buscar la equivalencia de 7 metros a kilómetros.
1 metro es equivalente a 1 décima parte de un decámetro, es decir, 0.1 decámetros, entonces dividimos 7 entre 10 y tenemos 0.7 decámetros. - 7 metros son equivalentes a 0.7 decámetros.
1 decámetro es equivalente a 1 décima parte de un hectómetro, es decir, 0.1 hectómetros, entonces dividimos 0.7 entre 10 y tenemos 0.07 hectómetros.
7 metros son equivalentes a 0.7 decámetros. - 0.7 decámetros son equivalentes a 0.07 hectómetros.
1 hectómetro es equivalente a 1 décima parte de un kilómetro, es decir, 0.1 kilómetros, entonces dividimos 0.07 entre 10 y tenemos 0.007 kilómetros. - 7 metros son equivalentes a 0.7 decámetros.
- 0.7 decámetros son equivalentes a 0.07 hectómetros y
- 0.07 hectómetros son equivalentes a 0.007 kilómetros.
Por lo tanto, 7 metros son equivalentes a 0.007 kilómetros (km).
Al buscar la equivalencia de 7 metros en kilómetros, estas estableciendo la equivalencia entre una unidad menor con una mayor.
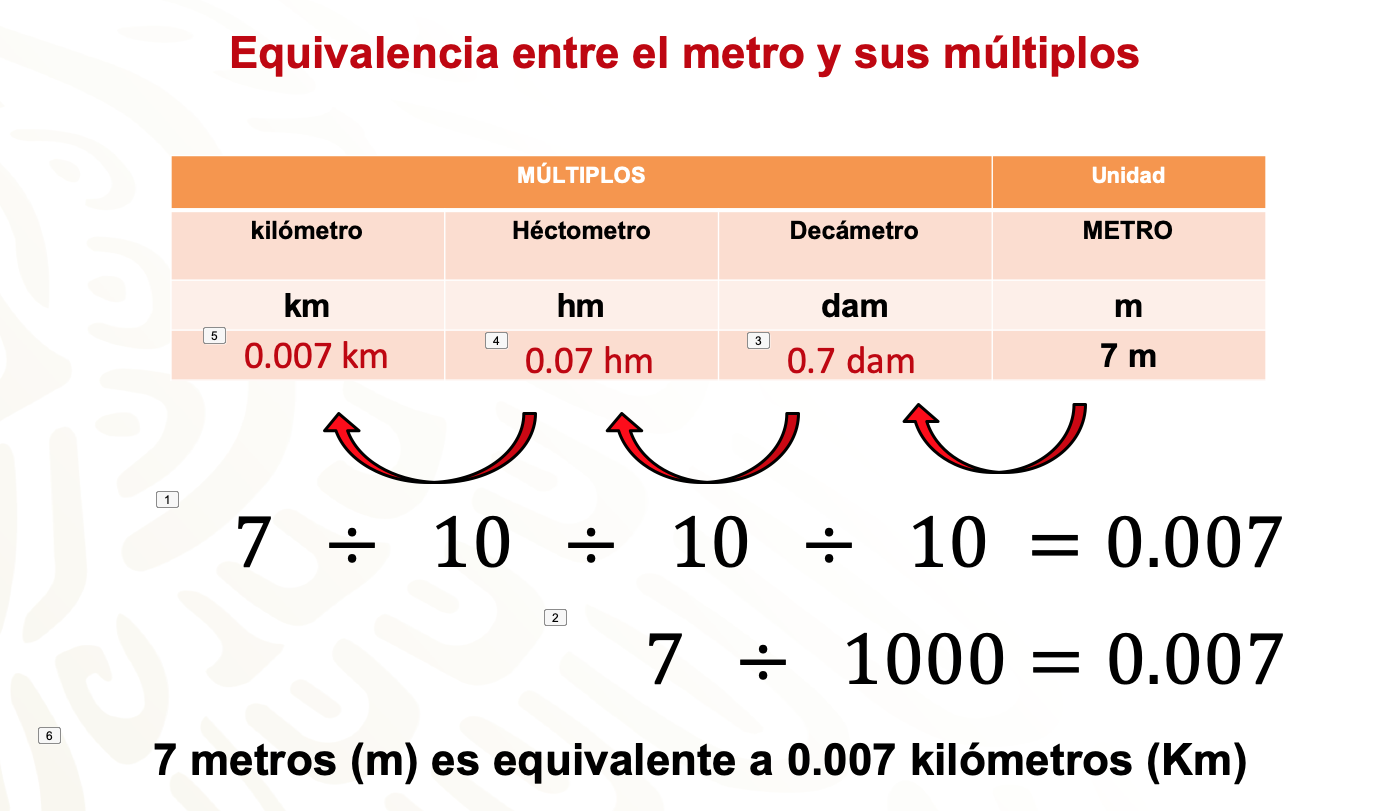
Como en la tabla hay tres lugares entre los m y los km, para encontrar la equivalencia dividimos 7 entre 1 000. Al dividir 7 ÷ 1 000 obtenemos como resultado 0.007 km.
Entonces 7 metros (m) es equivalente a 0.007 kilómetros (km).
Como conclusión podemos decir que, al realizar conversiones entre unidades, tenemos que:
- Para convertir de una unidad mayor a una menor, se multiplica.
- Para convertir de una unidad menor a una mayor, se divide.

Aplica lo estudiado para resolver la siguiente actividad:
Abril, Sandra y Luis compraron cuerda para saltar.
Abril compró una cuerda que mide 238 cm de longitud, Sandra compró una cuerda que mide 31 decímetros y Luis compró una cuerda cuya longitud es de 2.2 metros.
¿Quién compró la cuerda de mayor longitud?
Al unir sus cuerdas, ¿cuál es la máxima longitud total que se podría obtener suponiendo que se usan grapas y no nudos para unirlas?
¿Cuál es la diferencia de medida entre la cuerda de abril y la cuerda de Luis?
En la situación tienes medidas en metros y en submúltiplos del metro; para operar matemáticamente con estos datos, es necesario tenerlos en la misma unidad, para ello se requiere establecer su equivalente.
Debes convertir 238 cm a metros, que es lo que mide la cuerda de abril y convertir 31 decímetros a metros, que es lo que mide la cuerda de Sandra. La medida de la cuerda de Luis ya está dada en metros y mide 2.2 metros.
Comienza con la cuerda de abril, de 238 centímetros a metros.
En este caso vas a convertir de centímetros a metros, es decir, de una unidad menor a una mayor, y como se ve en la tabla, hay dos lugares de diferencia entre una y otra unidad, por lo que dividiremos entre 10 y luego entre 10, o dividiremos entre 100.
Al dividir 238, entre cien, el resultado es 2.38, lo que significa que 238 centímetros equivalen a 2.38 metros.

Al convertir 31 decímetros a metros dividirás entre 10, porque al observar la tabla verás que hay un lugar de diferencia. 31 entre 10 es igual a 3.1, por lo tanto, 31 decímetros equivalen a 3.1 metros.
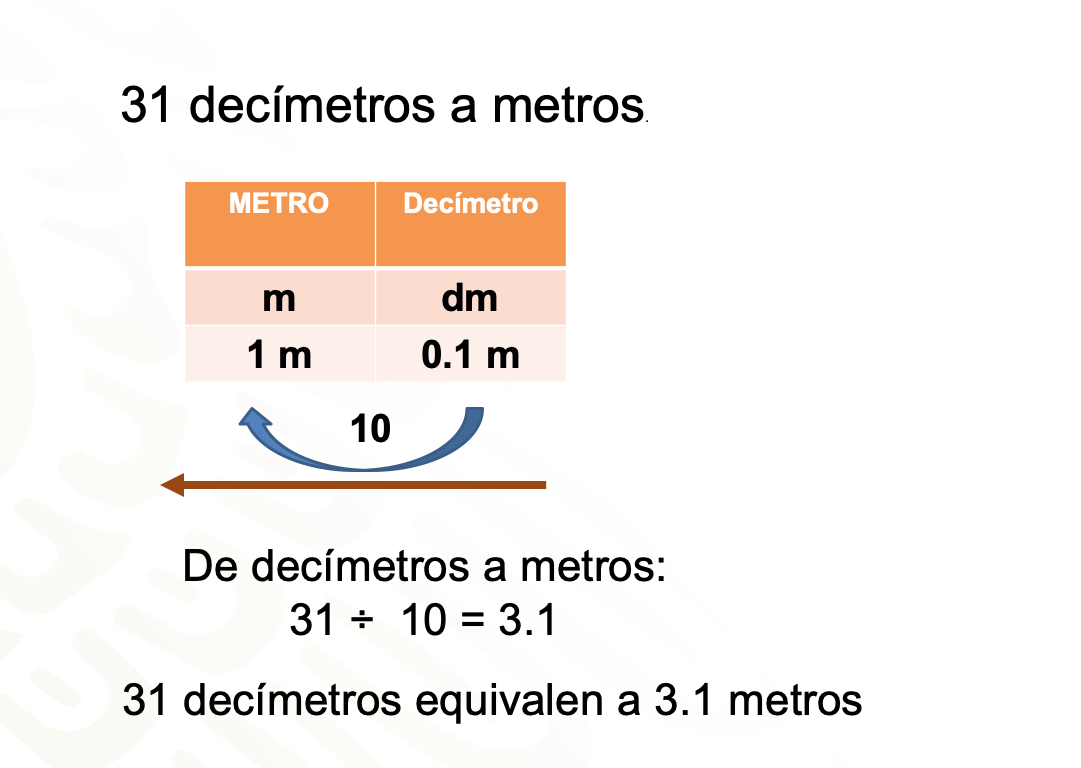
Ya has convertido las longitudes de las cuerdas a metros.
Da respuesta a las cuestiones planteadas por el reto que se te presentó.
¿Cuál es la cuerda de mayor longitud?
La cuerda de abril mide 2.38 metros.
La cuerda de Sandra mide 3.1 metros.
La cuerda de Luis mide 2.2 metros.
2.38 m es mayor que 2.2 m, pero menor que 3.1 m.
3.1 m > 2.38 m < 2.2 m
Por lo tanto, la cuerda de mayor longitud es la que compró Sandra.
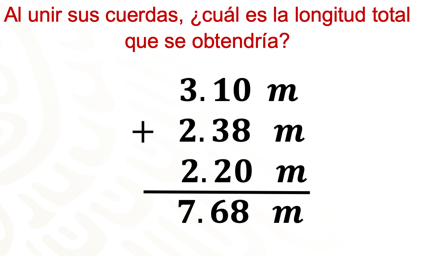
Al unir sus cuerdas, ¿cuál es la longitud total que se obtendría?
La suma de 3.1 metros, 2.38 metros y 2.2 metros es igual a 7.68 metros.
La máxima longitud total sería de 7.68 metros.
¿Cuál es la diferencia de medida entre la cuerda de abril y la cuerda de Luis?
La diferencia entre 3.1 metros, que es la medida de la cuerda de Luis, y 2.38 metros, que es la longitud de la cuerda de abril, es 0.72 metros.

Realizar conversiones de unidades es una técnica que nos permite operar con medidas cuando no todas están dadas en la misma unidad. Lo que hiciste en el reto anterior fue convertir de submúltiplos a la unidad fundamental base, el metro, por esa razón es que la conversión fue a partir de la división.
Realizar conversiones de unidades es una técnica que te permite operar con medidas cuando no todas están dadas en la misma unidad. Lo que hiciste en la actividad anterior fue convertir de submúltiplos a la unidad fundamental base, el metro, por esa razón es que la conversión fue a partir de la división.
Resuelve algunos ejemplos más.
Un corredor participa en una carrera de 12 kilómetros, hasta ahora ha recorrido 65 decámetros. ¿Cuántos metros le quedan por recorrer?
La distancia total es dada en kilómetros y lo que ha recorrido, en decámetros. Ahora debes determinar la distancia que falta por recorrer, en metros.
Convierte a metros para poder operar matemáticamente y determinar cuánto le queda por recorrer.
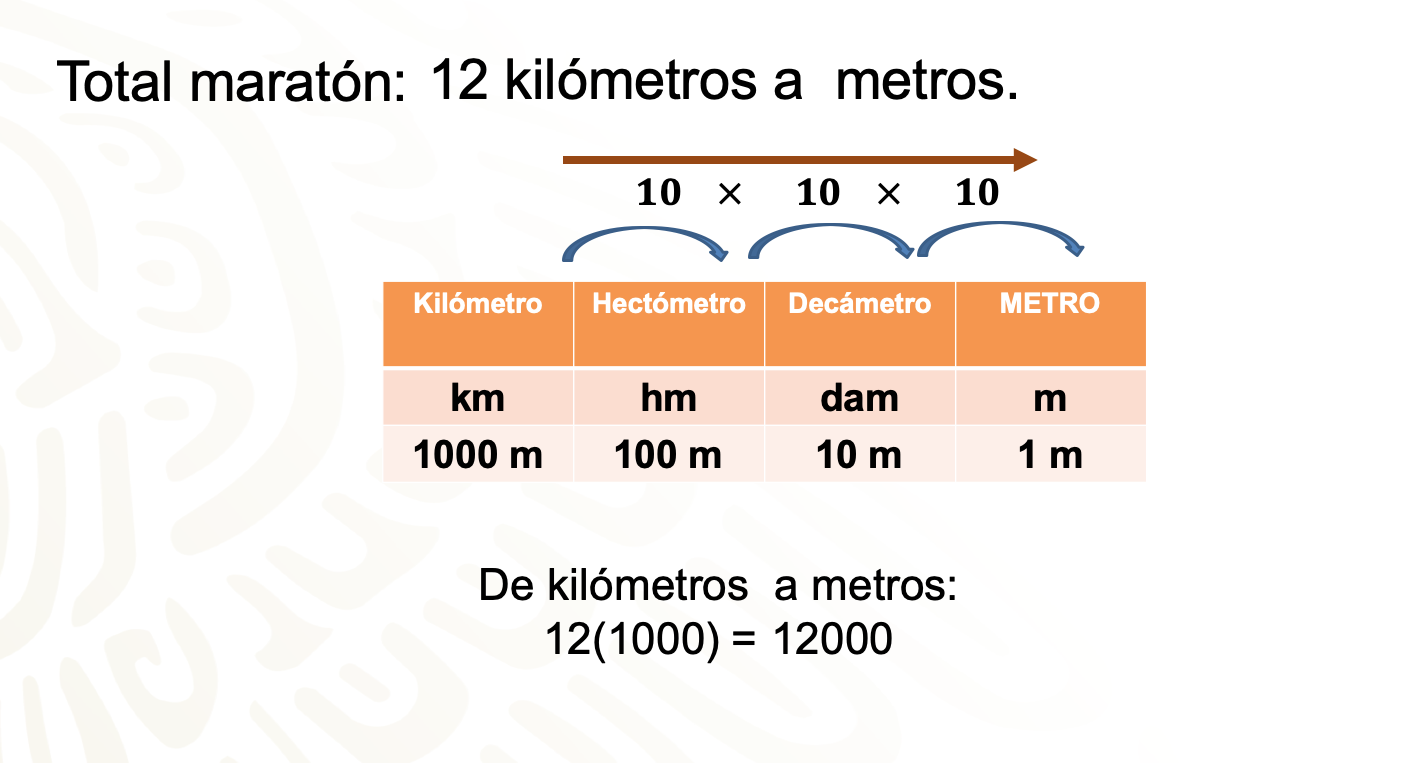
Distancia total de la carrera: 12 kilómetros a metros.
Realizarás una conversión de una unidad menor a una mayor. Como hay tres lugares de separación entre los “km” y los “m”, realizarás una multiplicación por 1 000.
Es así como determinamos que 12 kilómetros equivalen a 12 000 metros.
Hasta el momento ha recorrido 65 dam.
Busca la equivalencia de 65 dam a metros.
Realizarás una conversión de múltiplos a metros, y hay un lugar de separación entre ellas, por lo tanto, multiplicarás por 10.
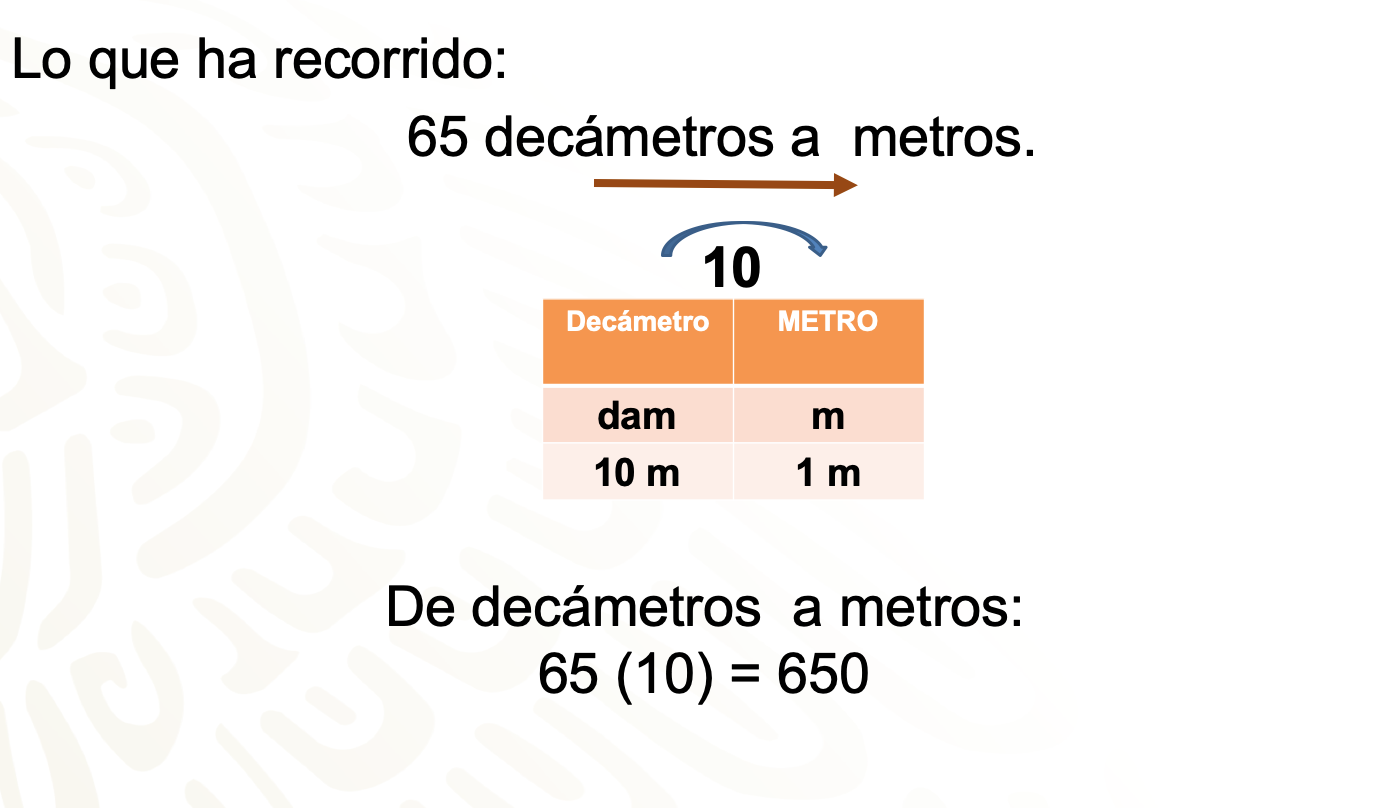
Es así como se determina que 65 decámetros equivalen a 650 metros.
Has convertido a metros el total de la longitud de la carrera y también convertiste a metros la distancia que ha recorrido hasta el momento.
Ahora determina cuánto le falta por recorrer, y esto será a través de la diferencia entre el total de la carrera y lo que ha recorrido.
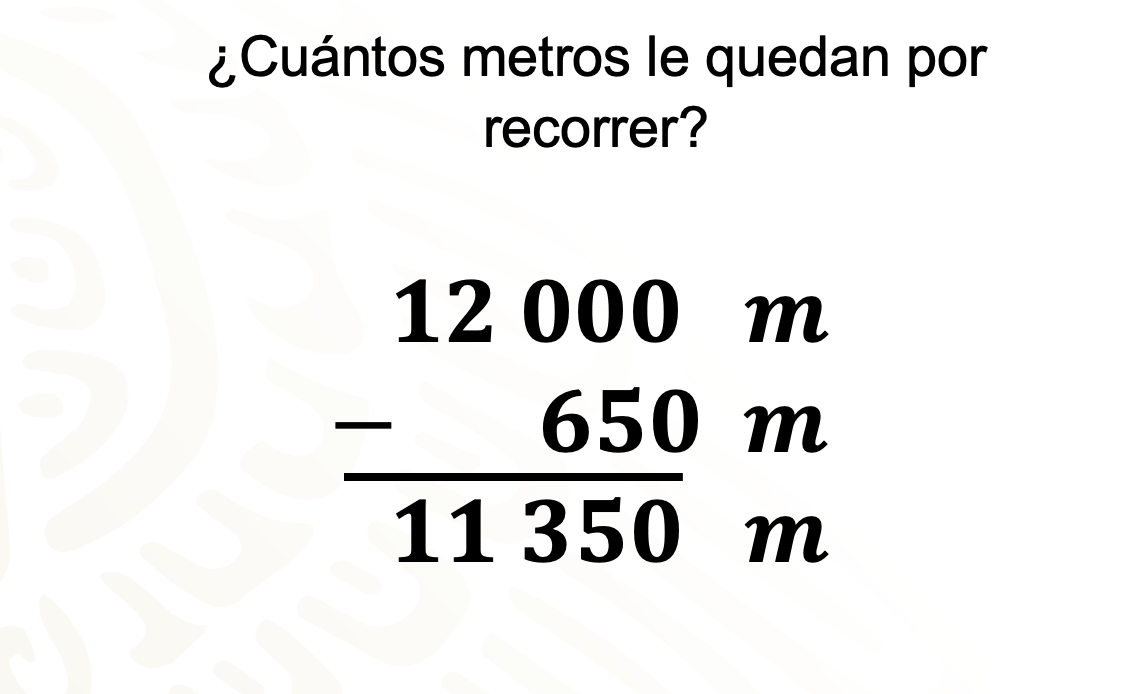
¿Cuántos metros le quedan por recorrer?
Debe recorrer 12 000 metros y ha recorrido 650 metros, al restar estas cantidades obtenemos que le faltan por recorrer 11 350 metros o 11.35 km, o 1135 dam.
Es importante que consideres que existen otras unidades de longitud, como el año luz y el parecer para medir distancias astronómicas. Investiga su equivalencia con algún múltiplo del metro.
También existen unidades muy pequeñas, como el angstrom para medir distancias moleculares y atómicas. Investiga su equivalencia con el metro.
El reto de hoy:
Para fortalecer lo aprendido, realiza lo siguiente.
¿Cuál es la equivalencia en metros de las siguientes unidades de longitud?
- Año Luz
- Parsec
- Angstrom
Para resolverlo, puedes apoyarte con tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/