Educación financiera I. Uso racional de los recursos. Ahorro
Educación financiera I. Uso racional de los recursos. Ahorro
Aprendizaje esperado: desarrollar habilidades que les permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Énfasis: usar procedimientos matemáticos para tomar decisiones.
¿Qué vamos a aprender?
Prepara tu cuaderno de apuntes, lápiz y goma, así como tu libro de texto.
La educación financiera es el conjunto de herramientas y conocimientos prácticos que permiten administrar, incrementar y proteger tu patrimonio, así como tomar mejores decisiones económicas en las diferentes etapas de la vida.
En una encuesta hecha por la Comisión Nacional para la Protección y Defensa de los Usuarios de Servicios Financiero (Condusef), se preguntó a los participantes “Si hoy perdiera su principal fuente de ingresos, ¿por cuánto tiempo podría cubrir su nivel de gastos sin pedir dinero prestado?

Estos datos indican que son pocos quienes han adoptado el hábito del ahorro. Ahorrar es guardar una parte de los ingresos para utilizarla más adelante.
Existe el tipo de ahorro en función del ahorrador, por ejemplo, público, privado o nacional. También existen tipos de ahorro por objetivo, por ejemplo, para una emergencia, para la jubilación para los hijos o con un objetivo definido. En esta sesión aprenderás sobre el ahorro privado con un objetivo definido.
¿Qué hacemos?
El hábito del ahorro puede parecer ajeno a la práctica común. Es por esto que, en esta sesión, estudiarás aspectos a tomar en cuenta para ahorrar de forma planificada y con base en procedimientos matemáticos.

Para empezar, se establece una meta, es decir, ¿para qué se quiere el dinero? Puede ser para comprar un artículo, tomar unas vacaciones o para un imprevisto.
Una vez establecida la meta, el siguiente paso es definir un plan de ahorro. ¿qué criterios tomarías en cuenta para llevar a cabo ese plan?
En primer lugar, se toma en cuenta la cantidad con la que se comenzará el ahorro. A esta cantidad se le llama cantidad inicial.
En segundo lugar, se considera cada cuánto se aportará una cantidad al ahorro. A cada una de las fechas en la que se realiza una aportación, se le llama plazo.
Luego se toma en cuenta de cuánto será la cantidad que se aportará en cada plazo. A esta cantidad se le llama monto.
Para definir un plan de ahorro se considera la cantidad inicial, el plazo y los montos. Las decisiones que se tomen con respecto a cada uno de esos criterios dan lugar a diferentes tipos de planes de ahorro.
Por ejemplo, una persona puede decidir partir de una cantidad inicial, ahorrar de modo que el tiempo transcurrido entre una aportación y otra sea el mismo y que el monto siga una regla específica.
Una regla consiste en que, para cada plazo, la cantidad total ahorrada se calcule a partir de la cantidad ahorrada en el plazo anterior. Por ejemplo, en un determinado plazo la cantidad total ahorrada se obtiene sumando un monto fijo a la cantidad total ahorrada en el plazo anterior.
Para aclarar ideas analiza el caso de dos amigas, Claudia y Laura. Las dos se propusieron ahorrar la mayor cantidad de dinero en un tiempo determinado de acuerdo con sus posibilidades económicas.
Ambas amigas decidieron partir de una cantidad inicial, ahorrar un monto cada semana y que ese monto sea de tal manera que la cantidad ahorrada en un plazo se obtenga de sumar una cantidad fija a la cantidad ahorrada en el plazo anterior.
Siguiendo esas reglas, ambas se propusieron ahorrar la mayor cantidad posible en un determinado plazo.

Realiza una estimación. ¿Laura ahorrará más porque inicia con una cantidad mayor que Claudia? ¿Claudia ahorrará más porque el monto semanal es mayor que el de Laura? ¿Ninguna de esas opciones es correcta?
¿Cuál sería la estrategia para responder las preguntas?
Para resolver el problema, una primera estrategia puede consistir en representar los datos en una tabla.
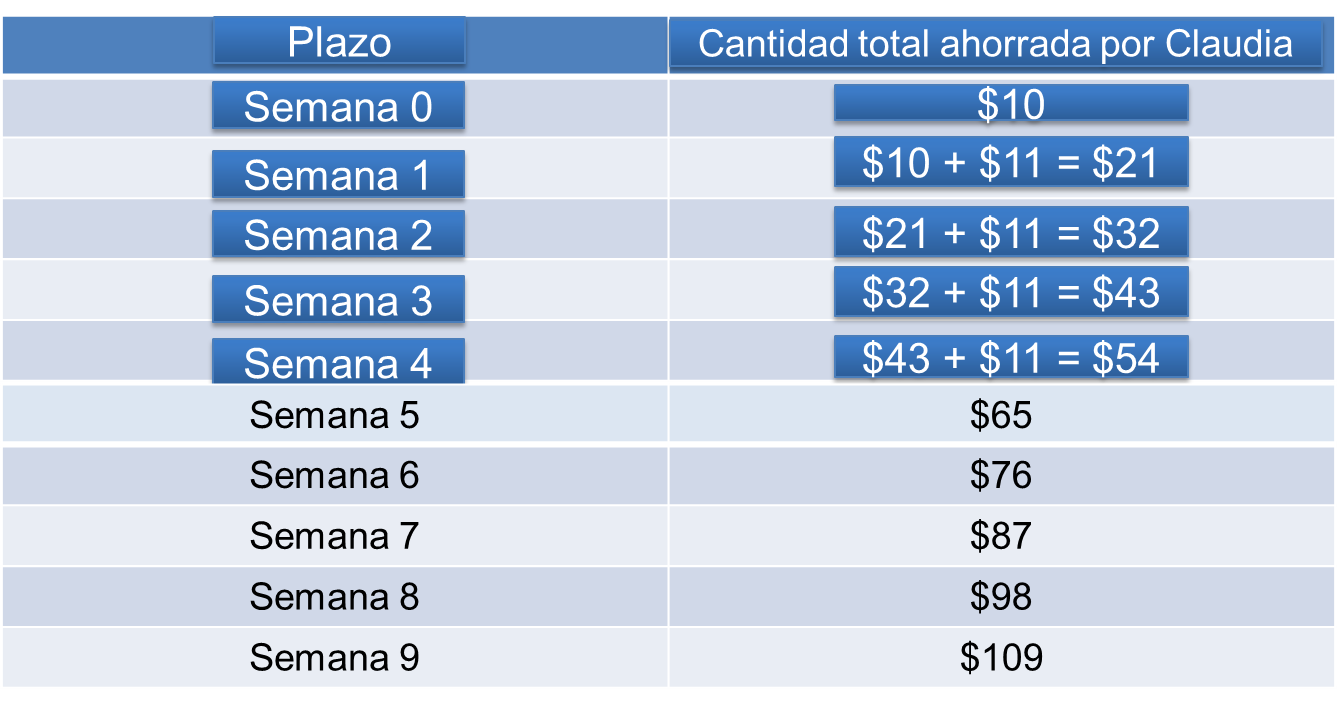
En la primera columna se anotan los plazos, cantidad inicial o semana 0, semana 1, semana 2, semana 3 y así sucesivamente. En la segunda columna se anota la cantidad final ahorrada para cada plazo. Recuerda que la regla acordada es sumar un monto fijo a la cantidad ahorrada en el plazo anterior.
En el caso de Claudia, la cantidad inicial es 10 pesos. Para obtener la cantidad ahorrada en la semana 1, se suman 11 pesos, que es la cantidad fija que decidió ahorrar Claudia, a 10 pesos, que es la cantidad ahorrada en el plazo anterior. Así, en la semana 1 Claudia tendrá una cantidad ahorrada de 21 pesos.
Para obtener la cantidad ahorrada en la semana 2, se suman 11 pesos, que es la cantidad fija que decidió ahorrar Claudia, a 21 pesos, que es la cantidad ahorrada en el plazo anterior. Así, en la semana 2 Claudia tendrá una cantidad ahorrada de 32 pesos.
Para obtener la cantidad ahorrada en la semana 3, se suman 11 pesos, que es la cantidad fija que decidió ahorrar Claudia, a 32 pesos, que es la cantidad ahorrada en el plazo anterior. Así, en la semana 3 Claudia tendrá una cantidad ahorrada de 43 pesos. Continúa con el llenado de la tabla.
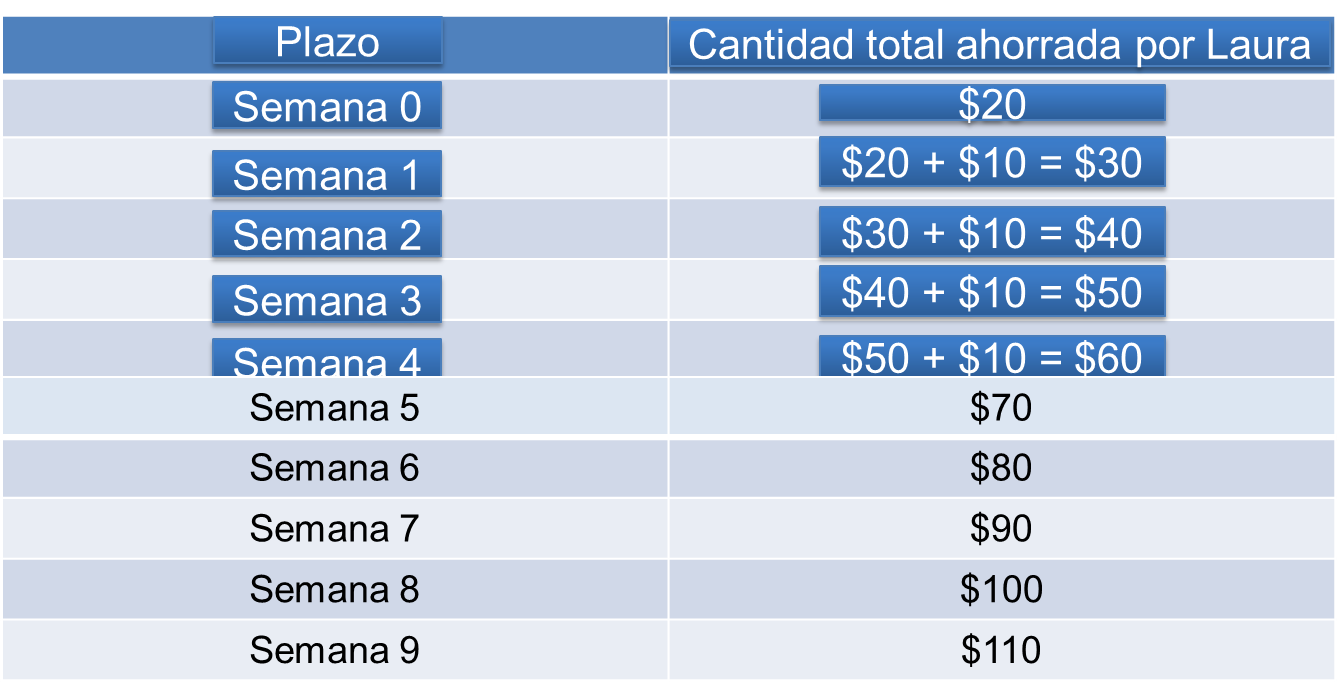
En el caso de Laura, la cantidad inicial es de 20 pesos. Para obtener la cantidad ahorrada en la semana 1, se suman 10 pesos, que es la cantidad fija que decidió ahorrar Laura. Así, en la semana 1 Laura tendrá una cantidad ahorrada de 30 pesos.
Para obtener la cantidad ahorrada en la semana 2, se suman 10 pesos a 30 pesos. Así, en la semana 2 Laura tendrá una cantidad ahorrada de 40 pesos. Para obtener la cantidad ahorrada en la semana 3, se suman 10 pesos a 40 pesos. Así, en la semana 3 Laura tendrá una cantidad ahorrada de 50 pesos.
Reflexiona. ¿Cómo apoya la tabla para averiguar quién ahorró más en un tiempo determinado? ¿qué otras estrategias utilizarías, además de la tabla?
Un análisis de la tabla aporta información sobre cuál plan de ahorro genera una cantidad mayor, en un plazo determinado.
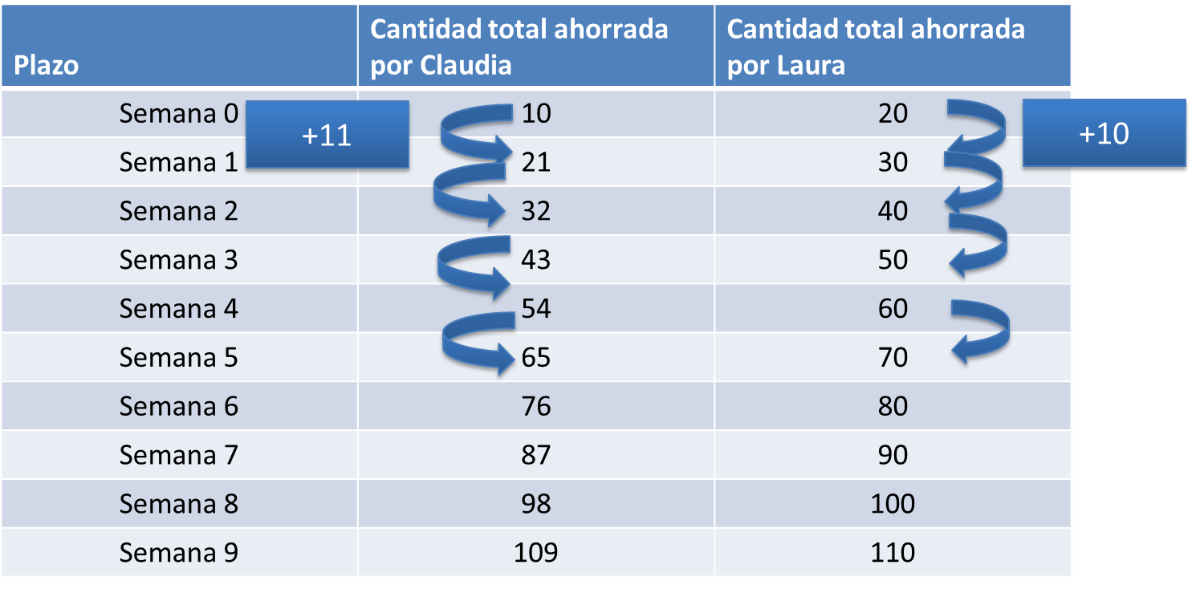
Supón que únicamente se tabulan los nueve primeros plazos. Se observa que, aunque en cada plazo la cantidad total ahorrada por Laura es mayor que la cantidad total ahorrada por Claudia, la cantidad total ahorrada por Claudia se acerca cada vez más a la cantidad total ahorrada por Laura.
¿Qué hipótesis podrías plantear a partir de la información de la tabla? Se podría conjeturar que en algún plazo la cantidad total ahorrada por Claudia superará a la de Laura.
Para probar la conjetura, se podría continuar con la tabla de valores. Pero, además, para tener una visión global de lo que sucede, una gráfica de los planes de ahorro puede ser de utilidad. ¿Cómo harías para graficar los planes de ahorro?
Primero toma en cuenta la forma en que varían los planes de ahorro. ¿Cómo aumenta la cantidad total de dinero ahorrada entre una semana y otra?
Observa que, en ambos casos, siempre se aumenta la misma cantidad de una semana a otra. En el caso de Claudia, la cantidad total ahorrada aumenta en 11 pesos y en el caso de Laura la cantidad total ahorrada aumenta siempre en 10 pesos.
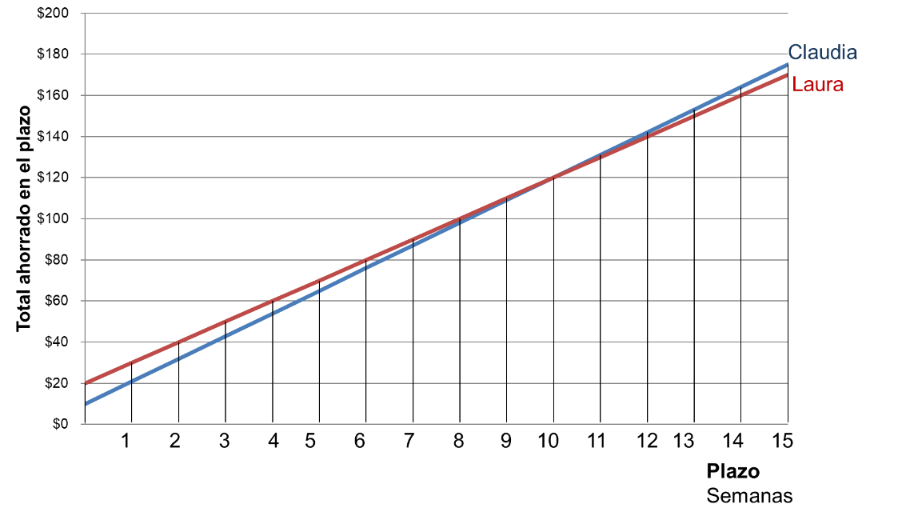
De acuerdo con lo anterior, la relación entre el número de plazos y la cantidad ahorrada es una relación lineal. Por tanto, la gráfica de cada plan de ahorro es una línea recta. Una vez considerado esto, basta con tomar dos puntos de cada plan de ahorro y unirlos.
En la gráfica se observa que, aunque en el plan de ahorro de Laura se inicia con una cantidad mayor que en el plan de ahorro de Claudia, en la décima semana la cantidad total ahorrada por Laura es igual a la cantidad ahorrada por Claudia y, a partir de la décimo primera semana, la cantidad total ahorrada por Claudia es mayor.
Con base en lo anterior, se llega a la conclusión de que, en el caso de los planes de ahorro analizados, un plan de ahorro no siempre produce una cantidad mayor que otro. Como se vio, en los primeros nueve plazos, el plan de Laura produce una cantidad total mayor, pero a partir de la décimo primera semana es el plan de ahorro de Claudia el que produce una cantidad total mayor.
Ahora bien, supón que ambas amigas decidieron mantener las condiciones de su plan de ahorro, parten de una cantidad inicial, ahorran un monto cada semana y ese monto es de tal manera, que la cantidad ahorrada en un plazo se obtiene de sumar una cantidad fija a la cantidad ahorrada en el plazo anterior.

En general, es importante que cuentes con una expresión algebraica que te permitiera conocer el número de plazos para ahorrar una determinada cantidad final con un monto específico o que te permitiera conocer el monto a ahorrar conociendo el número de plazos y la cantidad final.

Si se representa con la letra “i” como la cantidad inicial; “m” el monto fijo aplicado en cada plazo, y “n” el número de plazo se tiene lo siguiente.
Para el plazo cero, se parte de la cantidad inicial. Esto se representa como cantidad total ahorrada en el plazo cero igual a “i” (que representa la cantidad inicial).
Para obtener la cantidad total ahorrada en el plazo uno, recuerda que se suma el monto fijo “m” a la cantidad total ahorrada en el plazo anterior. Como la cantidad ahorrada en el plazo cero es “i” (que representa la cantidad inicial), para el primer plazo se tiene que la cantidad final ahorrada es igual a la cantidad inicial más el monto fijo. Algebraicamente, esto se representa como “i” más “m”.
Para obtener la cantidad total ahorrada en el plazo dos, se suma el monto fijo “m” a la cantidad total ahorrada del plazo anterior. Como la cantidad ahorrada en el primer plazo se representa como “i” más “m”, la cantidad total ahorrada en el plazo dos, se representa como “i” más “m” más “m”. Esto es igual a “i” más dos veces “m”.
Para obtener la cantidad total ahorrada en el plazo tres, se suma el monto fijo m a la cantidad total ahorrada en el plazo anterior. Como la cantidad ahorrada en el plazo dos se representa como “i” más dos “m”, la cantidad total ahorrada en el plazo tres, se representa como “i” más dos “m” más “m”. Esto es igual a “i” más tres veces “m”.
Para obtener la cantidad total ahorrada en un plazo “n”, se observa que las expresiones obtenidas para cada plazo son de la forma “y = mx + b”, en donde “y” es la cantidad total ahorrada en el plazo n, b es la cantidad inicial “i” y “m” es el monto fijo.
En resumen, si en un plan de ahorro se parte de una cantidad inicial, se ahorra un monto cada semana y ese monto es de tal manera que la cantidad ahorrada en un plazo se obtiene de sumar una cantidad fija a la cantidad ahorrada en el plazo anterior, entonces la cantidad total ahorrada “y” en el plazo “n” es igual a “i” más “n” por “m”, en donde “i” es la cantidad inicial, “m” es el monto fijo y “n” es el número de plazo.
Esta expresión algebraica es de utilidad para contestar la pregunta sobre el tiempo que se requiere para ahorrar una cantidad de 4 022 pesos, si la cantidad inicial fuera de 200 pesos y cada semana se abonaran 78 pesos al ahorro.
Pero ¿cómo se resuelve esta pregunta?
El plan de ahorro que acordaron Claudia y Laura se modela con la expresión cantidad total ahorrada “y” en el plazo “n” es igual a “i” más “m” por “n”, en donde “i” representa la cantidad inicial, “m” representa el monto fijo y “n” representa el número de plazo.
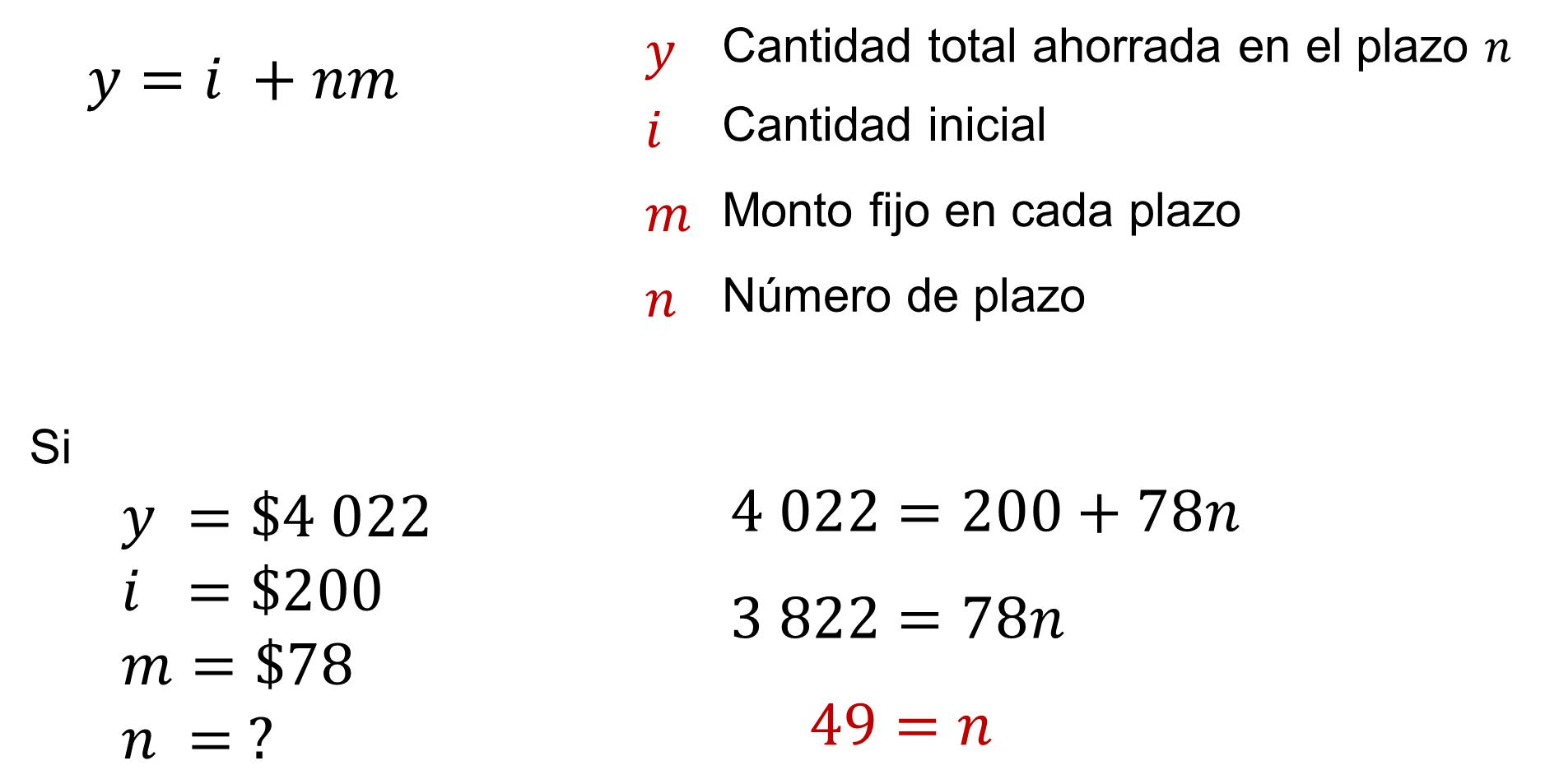
En el caso del problema “y” toma el valor de 4 022 pesos, “i” es igual a 200 pesos, “m” es igual a 78 pesos y “n” es la incógnita del problema.
Para encontrar el valor de la incógnita se utilizan las propiedades de la igualdad. Específicamente, si se resta 200 a ambos miembros se obtiene tres mil ochocientos veintidós igual a setenta y ocho “n”. Luego, si se dividen ambos miembros entre 78 se obtiene cuarenta y nueve igual a “n”.
Por tanto, para reunir la cantidad deseada con las condiciones establecidas se requieren cuarenta y nueve semanas, es decir, casi un año.
Hasta aquí, se ha analizado solo un tipo de plan de ahorro que, como se vio, se modela con relaciones lineales. Sin embargo, hay otros tipos de plan de ahorro.
Ya sabes que para definir un plan de ahorro se considera la cantidad inicial, el plazo y los montos. Las decisiones que tomen con respecto a cada uno de esos aspectos dan lugar a diferentes tipos de planes de ahorro.
Por ejemplo, se puede decidir partir de una cantidad inicial, ahorrar de modo que el tiempo transcurrido entre una aportación y otra sea el mismo y que el monto a aportar siga una regla específica.
Una regla puede consistir en que, para cada plazo, la cantidad ahorrada se calcule a partir de la cantidad ahorrada en el plazo anterior.
Específicamente, en el plazo uno se suma un monto “m” a la cantidad inicial, y en cada uno de los siguientes plazos se entrega un monto igual al del plazo anterior más “m”.
Pero ¿cómo se plantea un plan de ahorro siguiendo esta regla?
La regla consiste en que, en el plazo uno se entrega un monto “m” y, en los siguientes plazos, se entrega un monto igual al del plazo anterior más “m”. Así, si en el plazo uno se entrega un monto “m”, en el plazo siguiente se entregará un monto de 2m.
Para plantear un plan de ahorro con esta regla, puedes apoyarte de una tabla.

Supón que parten de una cantidad inicial “i” de 200 pesos y que en el plazo uno se entrega un monto “m” de 10 pesos. Entonces, en el plazo uno se tendrá una cantidad total ahorrada de 210 pesos.
Siguiendo la regla, si en el plazo uno se entrega un monto “m”, en el plazo 2 se entregará un monto de “m+m” o “2m”. Como el monto “m” es de 10 pesos, el monto en el plazo 2 es de 2 por 10 pesos igual a 20 pesos. Entonces, en el plazo dos se tendrá una cantidad total ahorrada de 230 pesos.
Continuando con la regla, si en el plazo dos se entrega un monto de 2m, en el plazo 3 se entrega un monto de 2m más m igual a 3m. Como el monto m es de 10 pesos, el monto en el plazo 3 es de 3 por 10 pesos igual a 30 pesos. Entonces, en el plazo tres se tendrá una cantidad total ahorrada de 260 pesos.
Continúa con el llenado de la tabla.
Si analizas el plan de ahorro, ¿se podrá modelar con una relación lineal?, ¿por qué?
Observa que la diferencia total ahorrada entre un plazo y otro no es la misma. Entre el plazo cero y el plazo uno, la cantidad total ahorrada difiere diez pesos. Entre el plazo uno y el plazo 2, la cantidad total ahorrada difiere 20 pesos, pero entre el plazo dos y el plazo tres la cantidad total ahorrada difiere 30 pesos.
Ahora bien, si se analizan las segundas diferencias, se observa que siempre es la misma. ¿Qué se concluye de esto?
Que el plan de ahorro se puede modelar como una relación cuadrática y que su gráfica será la rama de una parábola.
Para finalizar la sesión se planteará una situación sobre los planes de ahorro.
Se tienen dos planes de ahorro. En ambos planes se decide partir de una cantidad inicial, ahorrar de modo que el tiempo transcurrido entre una aportación y otra sea el mismo y que el monto siga una regla específica.
En el primer plan de ahorro se parte de una cantidad inicial de 10 pesos y, para cada plazo, se aporta un monto fijo. Ese monto fijo es de 5 pesos.
En el segundo plan de ahorro se parte de una cantidad de 10 pesos. Además, se entrega un monto “m” para el plazo uno y, en los siguientes plazos, se entrega un monto igual al del plazo anterior más “m”. El monto “m” que se entrega en el plazo 1 es de 5 pesos.

¿Qué monto fijo se tendría que depositar en el primer plan de ahorro para que la cantidad ahorrada en el plazo 6 de los dos planes sea la misma?
- 10.90 pesos
- 12.50 pesos
- 17.50 pesos
- 20.89 pesos
¿Cómo resuelves esta situación?
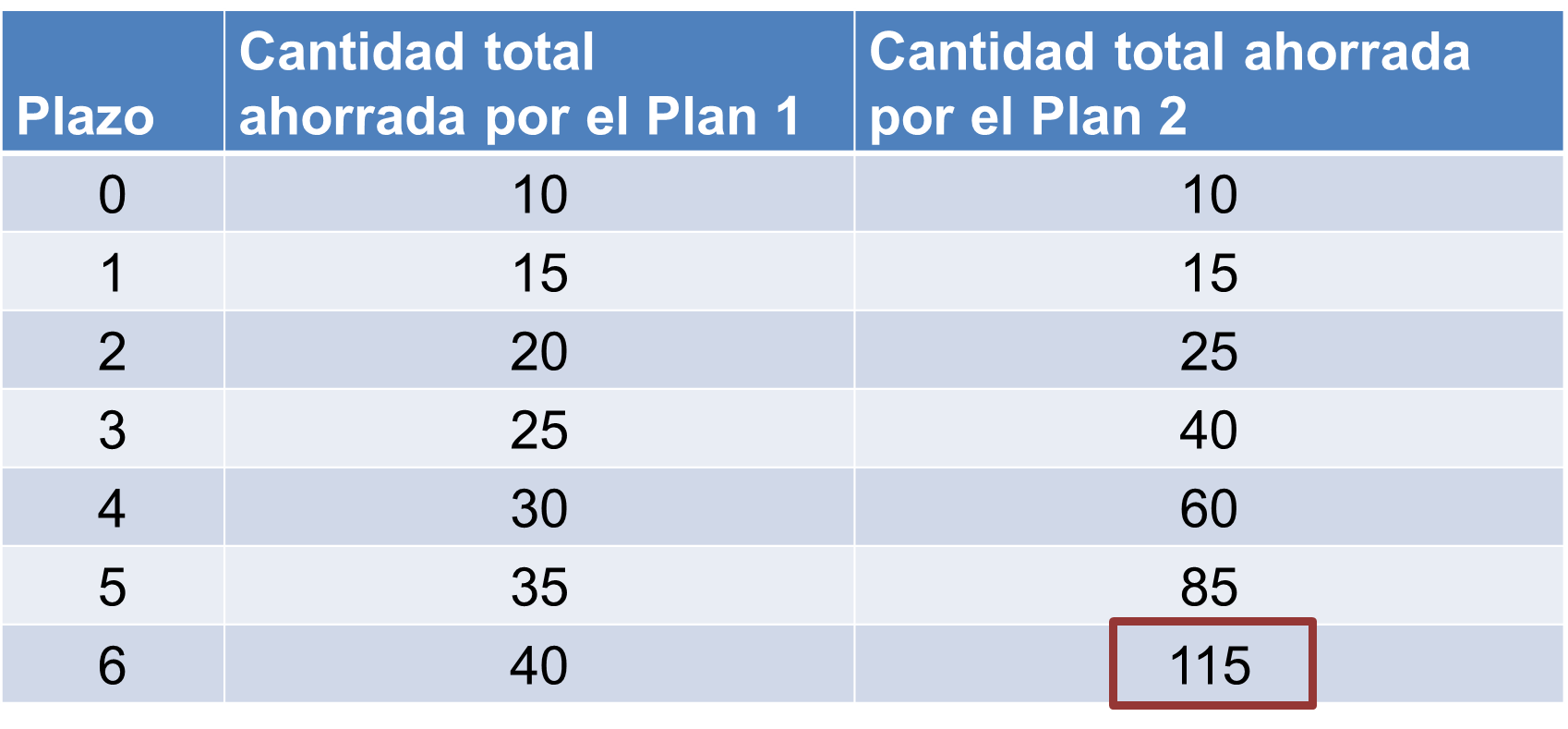
Para resolver el problema, te pueden apoyar en una tabla de valores de cada plan de ahorro hasta el sexto plazo. Se observa que, en el segundo plan de ahorro, la cantidad total ahorrada al sexto plazo es de 115 pesos.
Por otro lado, la expresión algebraica que modela el primer plan de ahorro en el sexto plazo es cantidad total ahorrada en el sexto plazo igual a “10+6m” donde “m” es el monto en un número de plazo. Como se quiere que la cantidad total ahorrada en ese plazo sea de 115 pesos, entonces la expresión algebraica que resuelve el problema es “115=10+6m”, donde “m” representa el monto a abonar. Al resolver la ecuación se tiene que “m” es igual a 17.50 pesos.
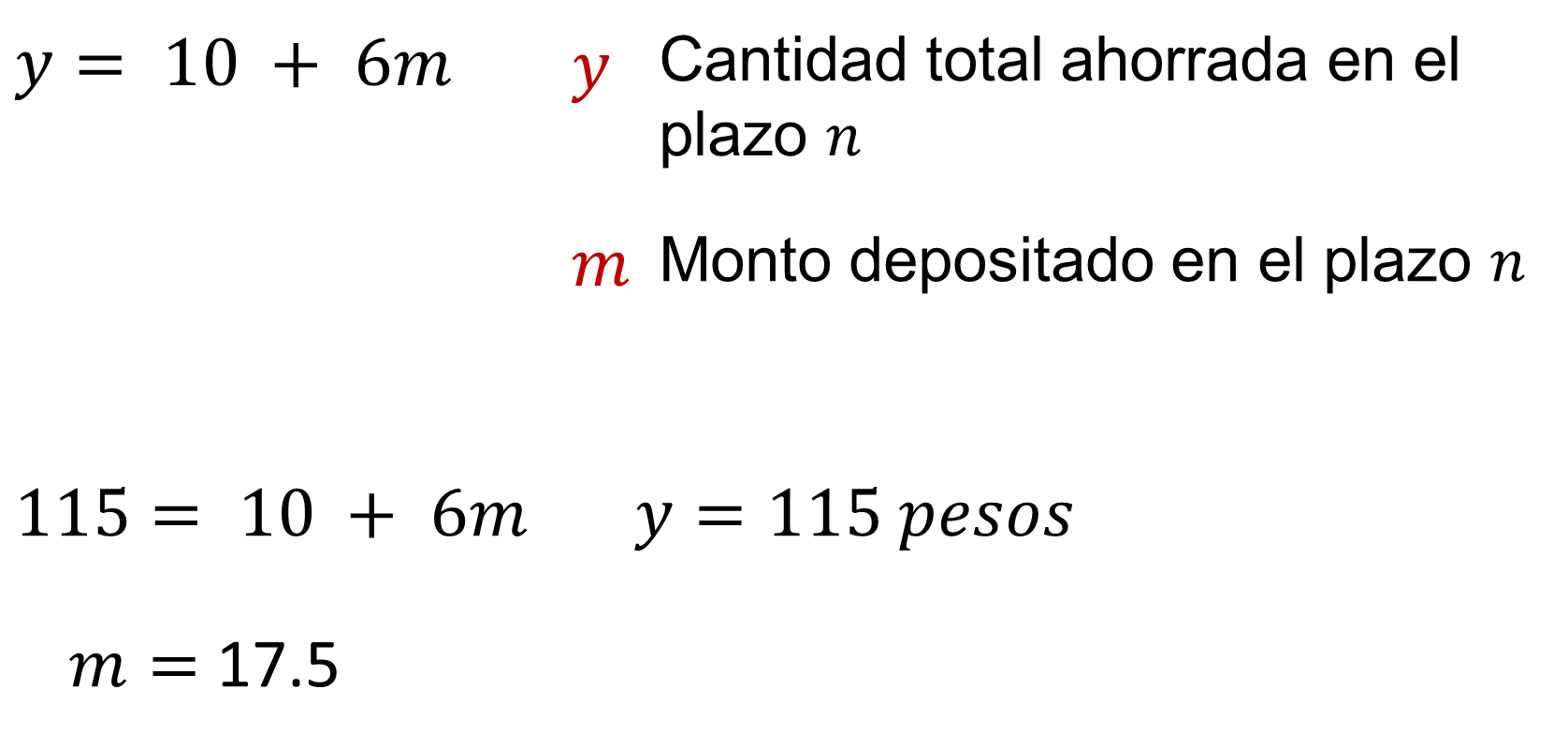
Si se elige la opción “A”, el error se encuentra en el planteamiento de la expresión que modela el primer plan de ahorro. Específicamente, en lugar de plantear la expresión “115=10+6m”, se plantea la expresión “115=6+10m”.
Si se elige la opción “D”, el problema se modela correctamente, pero la resolución de la ecuación es incorrecta. Específicamente, en la expresión “115=10+6m”, en lugar de restar 10 a ambos miembros, se suma 10 en lado izquierdo y se resta 10 al lado derecho.
El reto de hoy:
Has desarrollado habilidades para tomar decisiones relacionadas con distintos tipos de planes de ahorro. Con esto plantea y enfrenta situaciones no rutinarias.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.